Critical dispersion of chirped fiber Bragg grating for eliminating time delay signature of distributed feedback laser chaos
Da-Ming Wang(王大銘), Yi-Hang Lei(雷一航), Peng-Fei Shi(史鵬飛), and Zhuang-Ai Li(李壯愛)
1School of Information,Shanxi University of Finance and Economics,Shanxi 030006,China
2School of Humanities,Communication University of Shanxi,Jinzhong 030619,China
Keywords: chaos,semiconductor laser,time delay signature,chirped fiber Bragg grating(CFBG)
1.Introduction
Owing to the complex dynamic characteristics, the chaotic laser has great potential applications in secure communication,[1–4]key distribution,[5–10]random number generation,[11–15]and optical neural networks.[16–18]A common approach is to use an external cavity semiconductor laser to generate optical chaos.However, the external cavity mode introduced in the external cavity feedback causes the time delay signature (TDS) in chaotic laser and reduces its complexity.[19]
Many methods have been proposed to solve this problem,including special external cavity feedback,[20,21]and external nonlinear devices.[22–30]In the special external cavity feedback method, an ultrashort external cavity length[20]or two roughly equal cavities are proposed to hide TDS.[21]In the external nonlinear device method, the nonlinear response of a nonlinear device is utilized to reduce the correlation between the output light and the feedback light, such as an additional laser,[22]phased-array feedback,[23]phasemodulated feedback,[24,25]random grating feedback,[26]FBG feedback[27,28]and chirped FBG(CFBG)feedback.[29,30]
In previous study, we have found that dispersion is a meaningful parameter, and a reasonable setting can achieve the complete elimination of TDS.[29]The reason for the elimination of TDS is the nonlinear feedback caused by the dispersion of CFBG.Unlike the fixed external cavity feedback, the dispersive feedback brings an increasing delay time which is related to the resonance frequency.Although the CFBG feedback scheme has proven to be able to eliminate the TDS, the critical dispersion of CFBG is the key to generating a nonperiodic chaotic laser in practical application.It should be mentioned that previous work has paid attention to the mechanism of TDS elimination in which dispersive feedback light forms CFBG induced irregular external-cavity mode.By comparison, this work focuses on the critical dispersion range of CFBG which could eliminate the TDS of laser chaos.
In this work,the dispersion of CFBG and the internal parameters of a DFB laser are quantitatively analyzed.In addition,the relationship between these parameters and the critical dispersion is studied.An empirical formula for the critical dispersion of CFBG is obtained by using the modified Lang–Kobayashi model.The TDS can be eliminated in a wide area where the dispersion exceeds the critical dispersion value.Furthermore, these results provide important quantitative guidance for the design of chaotic semiconductor lasers.
2.Theoretical mode
The configuration of dispersion feedback of the DFB laser is illustrated in Fig.1.A CFBG is used to obtain the dispersion feedback light.The inset shows the group delay spectrum of CFBG and the optical spectrum.Numerical simulations are conducted by using the well-known Lang–Kobayashi equations.[31]By adding the dispersive feedback item, the modified rate equations can be written as follows:[29,30]
whereErepresents the slowly varying amplitude of the electrical field,Nbeing the carrier density,αbeing the linewidth enhancement factor,gbeing the differential gain,N0being the transparency carrier density,εbeing the gain saturation parameter,τpbeing the photon lifetime,τinbeing the roundtrip time in the laser cavity,κfbeing the amplitude feedback strength,qbeing the elementary charge,Vbeing the active layer volume,τNbeing the carrier lifetime, andτbeing the round-trip time between the laser and the grating.
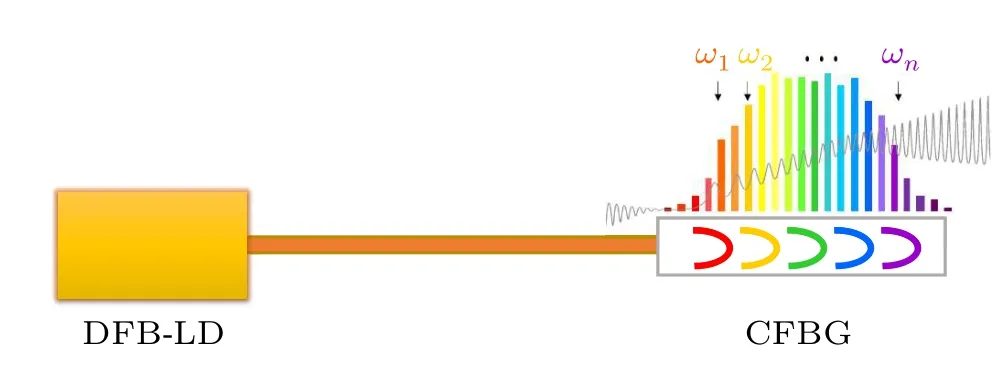
Fig.1.Schematic diagram of the DFB laser subjected to dispersive feedback from CFBG.
The CFBG feedback is described by the second term on the right-hand side of Eq.(1).The term varies with response functionh(t)of the CFBG convoluted with delayed laser fieldE(t-τ).Tdenotes the integral length and its length should be larger than the response time of grating.Since there is no analytical solution for the response function of CFBG,the dispersive feedback term can be computed by taking the inverse Fourier transform ofH(ω)·FT{E(t-τ)}according to the convolution theorem.Here, FT{ }is the Fourier transform.The reflection spectrumH(ω) can be calculated by using the piecewise-uniform approach.[29,32]It should be noted that the grating dispersion can be calculated from 100(dλ/dz)-1,with dλ/dz(nm/cm) representing the chirp factor of CFBG.The values of the parameters used in our simulation are summarized in Table 1.To quantify the TDS,the auto-correlation function(ACF)is expressed as
whereI(t)represents the intensity time series,I(t+Δt)is the time shift Δtwith respect toI(t), and〈·〉 denotes average.In the simulation, TDS is evaluated the height of ACF peak around the feedback delay time corresponds to the external cavity.
3.Results and discussion
The CFBG feedback method could eliminate TDS because of the nonlinear feedback from the feedback light.Both the DFB laser and the CFBG are two nonlinear sources in the CFBG feedback system.Therefore, we focus on the relationship between the group delay caused by the dispersion of CFBG and the laser.For the CFBG feedback light,the accumulated group delay of the feedback light can be calculated by using the dispersion and the bandwidth of the optical spectrum.The dispersion is determined by the chirp factor of the CFBG, and the bandwidth is affected by the bias current of the laser,the feedback strength,and the differential gain coefficient.
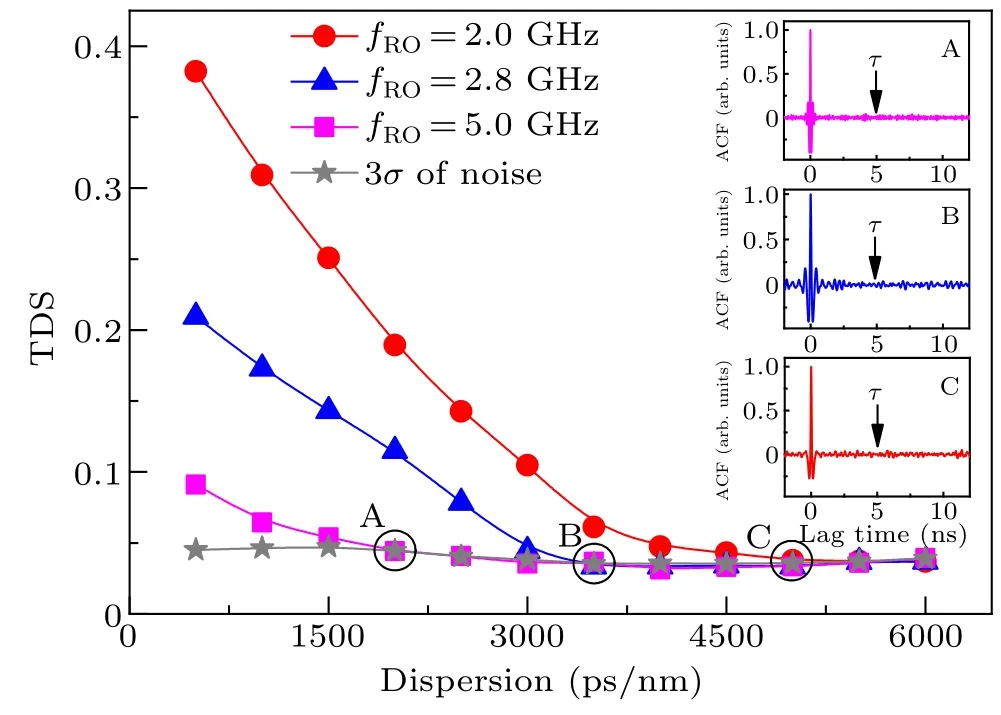
Fig.2.Results of TDS as a function of CFBG dispersion obtained at fRO values of 2.0 GHz(circle),2.8 GHz(triangle),and 5 GHz(square).Insets show the ACF curve of chaotic signal corresponding to points A, B, and C.I=1.5Ith,κf=0.1,and σ denotes the background noise of ACF curve.
Figure 2 shows the curves of TDS as a function of CFBG dispersion at relaxation oscillation frequency of 2.0 GHz(circle),2.8 GHz(triangle),and 5 GHz(square),respectively.The TDS value is extracted from the ACF traces near the feedback delay(τ-0.5,τ+0.5).The insets show the autocorrelation function(ACF)traces of the chaotic signal corresponding to points A, B, and C.It means that TDS can be eliminated at a feedback delay (5 ns).As the dispersion value increases, TDS gradually reduces until it is submerged in the background noise floor of the ACF curve.In addition,the results of the three values of relaxation oscillation frequency,i.e.,fRO=2.0 GHz,2.8 GHz and 5.0 GHz,show similar evolution tendencies.Interestingly,the smaller critical dispersion can be obtained at a larger value offRO.
Figure 3 shows the effects of thefROand dispersion on the TDS.The colors denote the height of the side peak at the feedback delay time in the ACF curve, and the deeper color represents a lower TDS value.The TDS elimination region is obtained in the dark purple area with obvious boundaries.This boundary can be approximately fitted with a curve which is denoted by a white dashed line.With the increase offRO,the critical dispersion of eliminating the TDS decreases gradually.When thefROincreases from 2 GHz to 6 GHz,the critical dispersion decreases from 5000 ps/nm to 1100 ps/nm,and the critical dispersion decreases by 78%.
According to the fitting curve, the relationship between critical dispersion(βc)andfROcan be expressed as
wherek(const.)is a constant and the fitted value is 10.Since the CFBG introduces the nonlinear effect from the optical domain, the relationship between the spectrum of chaotic light and thek(const.) is investigated in the following.
Figure 4 displays the spectra with differentfROvalues(2 GHz,3 GHz,4 GHz,5 GHz,5.5 GHz,and 6 GHz)at several critical dispersion points in Fig.3.The red curves in the optical spectrum of chaotic laser denote their mean fit.It is obvious that the linewidth(-3 dB)of the optical spectrum is roughly 0.1 nm which is exactly equal to the inverse of thek(const.).Therefore,the empirical formula for the critical dispersion can be given as follows:
whereΛ-3dBdenotes the linewidth of the optical spectrum at-3 dB.

Fig.3.Effects of parameters (fRO and dispersion) on TDS, with white dash line denoting critical dispersion of CFBG for eliminating TDS,I=1.5Ith,and κf=0.1.
To show the nonlinear effect caused by dispersion more clearly, the correlation between the output light and the dispersive feedback light is shown in Fig.5.Colors represent the values of the correlation peaks in the cross-correlation curve,and the degree of correlation decreases as the color deepens.Note that the white dash line delineates the critical dispersion range in Fig.3.The negative dispersive feedback compresses the pulse width in the time domain thus decreasing the value of correlation between the feedback light and the output light.Furthermore, the cross-correlation value gradually decreases as the relaxation oscillation increases.Besides,the correlation value of the feedback and output light ranges from 0.147 to 0.058 along the critical dispersion curve.That means that the critical dispersion value for eliminating TDS is determined by the combined result of both DFB laser and CFBG.
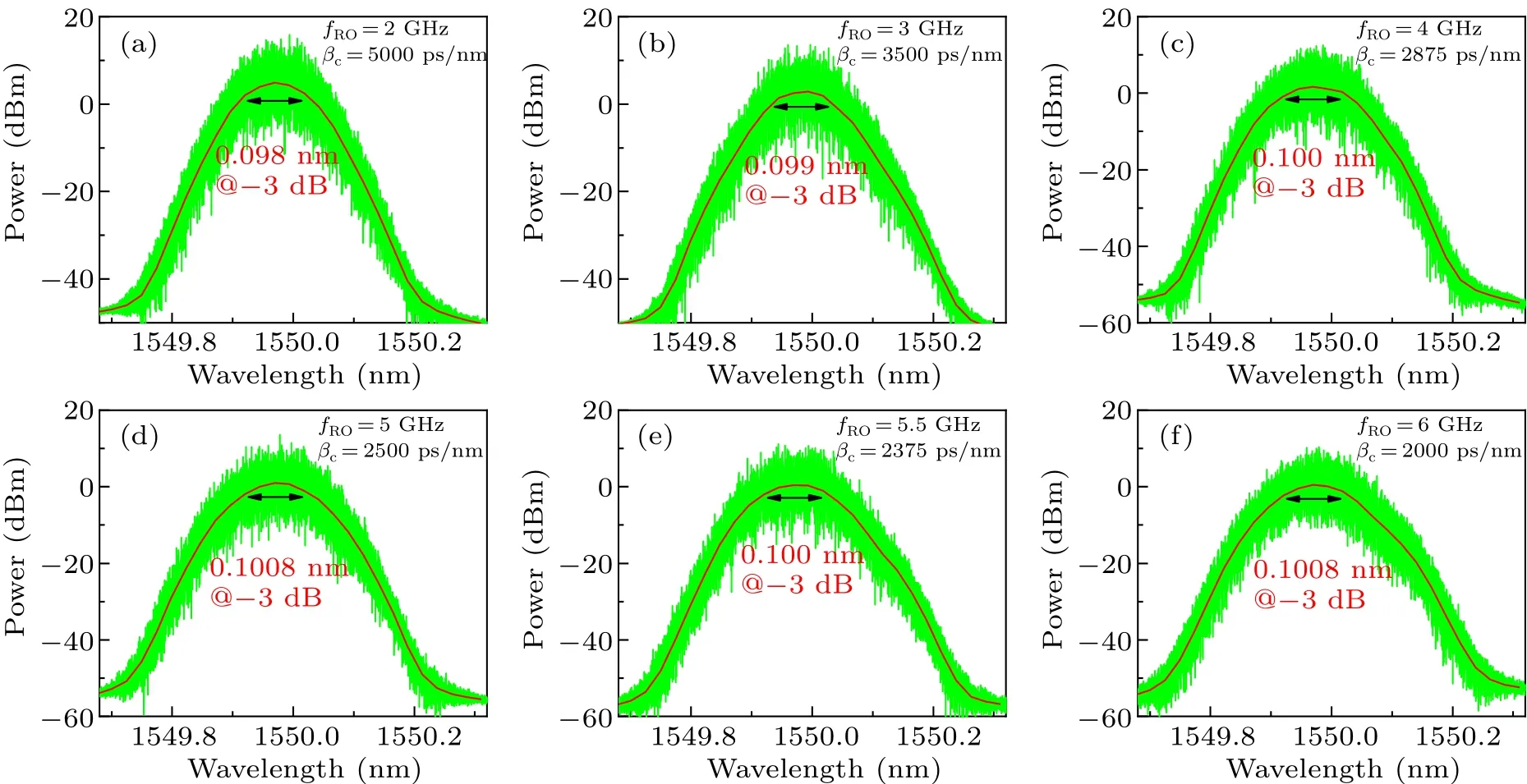
Fig.4.Numerical results of optical spectra at fRO values of(a)2 GHz,(b)3 GHz,(c)4 GHz,(d)5 GHz,(e)5.5 GHz,and(f)6 GHz.

Fig.5.Effects of parameters (fRO, dispersion) on cross-correlation coefficient of the output light and dispersive feedback light from CFBG.I=1.5Ith and κf=0.1.
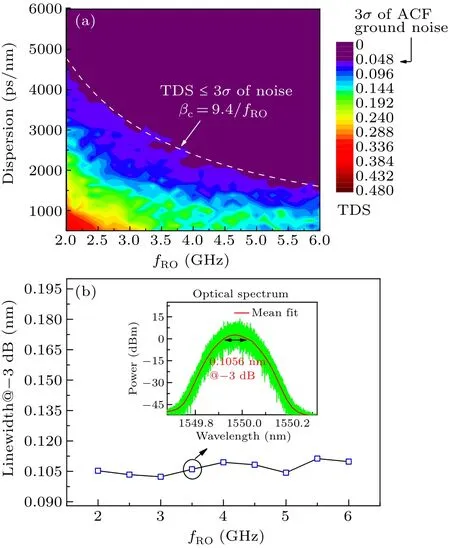
Fig.6.(a)Effects of parameters(fRO,dispersion)on TDS and(b)effects of fRO on line width of optical spectrum,with dashed line denoting critical dispersion of CFBG for eliminating TDS and insets showing optical spectrum of output light at I=1.5Ith and κf=0.12.
Furthermore, the results ofβcwith feedback strength of 0.12 are exhibited in Fig.6,including the effect offROand dispersion on TDS(Fig.6(a))and the effect offROon line width of the optical spectrum(Fig.6(b)).The inset shows the optical spectrum atfROof 3.5 GHz.It is obvious that the boundary of critical dispersion can be approximately fitted by the dash line(βc=9.4/fRO),where thek(const.)is equal to the inverse of the linewidth.Unlike Fig.3,the dash line shifts downward and there is a significant decrease withk(const.).The reason is that the optical spectrum has broadened askfincreases from 0.1 to 0.12.The increase of group delay caused by CFBG and optical spectrum will reduce the correlation between the feedback light and the output light.As a result,the system requires a lower dispersion to eliminate TDS andk(const.)will decrease significantly.
Furthermore, the above formula is verified by changing the bias current of the DFB laser, and the results are shown in Fig.7.Figure 7(a) shows the effect offROand dispersion on TDS.Figure 7(b) displays the effect offROon the linewidth (-3 dB) of chaotic light.The insets show two optical spectra under thefROof 2.5 GHz and 5.5 GHz, respectively.When thefROvalue is over 3.5 GHz, the critical dispersion can be approximately fitted as the white dashed line(βc= 6.9/fRO) which matches well with the inverse of the linewidth.For thefROvalue below 3.5 GHz, the linewidth gradually increases withfROincreasing.The critical dispersion can be correspondingly fitted with the curve related to the empirical formula (5) which is shown by the yellow dotted line in Fig.7(a).As a result, the empirical formula of critical dispersion is proved.In addition, the bandwidth of spectrum in Fig.7(b)is stable at about 0.144 nm when thefROover 3.5 GHz which means that the group delay induced by the CFBG will be stable.Therefore,βcfollows different formulas before and afterfROof 3.5 GHz.

Fig.7.(a)Effects of parameters(fRO,dispersion)on TDS and(b)effects of fRO on line width of optical spectrum,with dashed line denoting critical dispersion of CFBG for eliminating TDS,and insets showing optical spectrum of output light,at κf=0.1,and g=0.5625×10-3 μm3·ns-1.
It is worth noticing that thefROof a solitary laser(without external feedback)can be obtained according to Ref.[33].Therefore,fROis adjusted in the simulation with bias current and differential gain.Figure 8 shows the effect of bias current and differential gain onfRO.The bias current varies from 1.5Ithto 6Ith, and the differential gain varies from 0.0005 to 0.0045.In addition, it is considered that the feedback light slightly increases the relaxation oscillation frequency of the laser.In order to obtain a more accuratefRO, thefROin the simulation is obtained fromτROin the ACF curve (fRO=1/τRO)as shown in the inset of Fig.8.
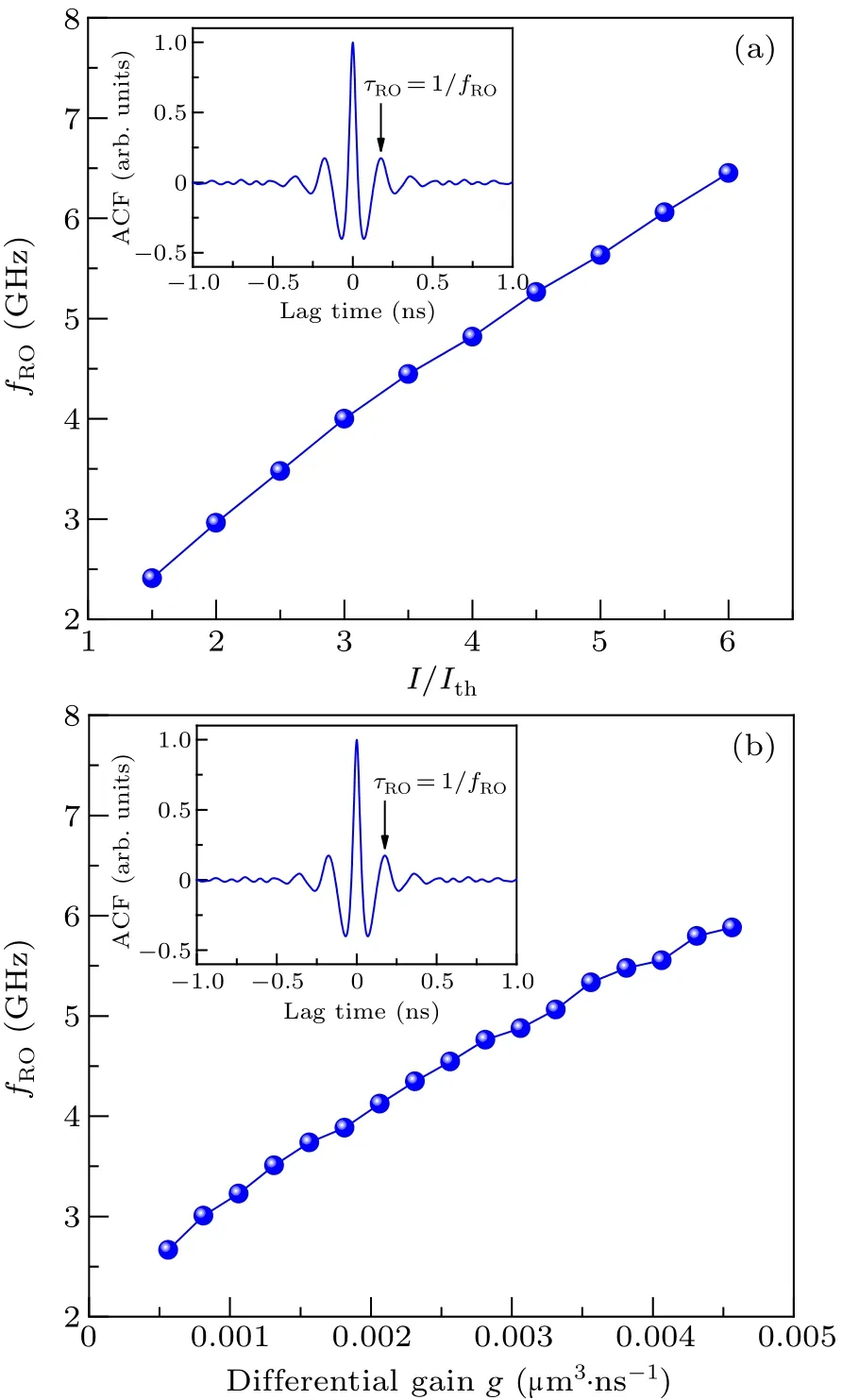
Fig.8.Effect of (a) bias current and (b) differential gain on fRO, with each of insets showing ACF curve of the chaotic laser output.
4.Conclusion
We conduct extensive simulations to investigate the TDS of a DFB laser with CFBG dispersive feedback, from which a critical dispersion for eliminating TDS can be determined.The nonlinearity in this system is obtained by the laser and the CFBG.For the dispersive feedback light, the external cavity mode will be destroyed while the value of group delay caused by dispersion from CFBG is greater than that ofτRO.At the same time, the output light shows that the TDS disappears.The results show that there is a clear demarcation line in the range where the TDS is eliminated and an empirical formula is obtained.Furthermore,through the analysis of the correlation between the feedback light and the output light,it is found that the elimination of TDS is the result of the joint action of both CFBG and DFB.This study provides a parameter setting basis for a semiconductor laser subjected to CFBG feedback to generate a TDS-free chaotic laser.
Acknowledgments
Project supported by the National Natural Science Foundation of China (Grant No.62105190), the Natural Science Foundation of Shanxi Province of China (Grant No.20210302124268),the Scientific and Technological Innovation Programs of Higher Education Institutions of Shanxi Province of China(Grant No.2021L285), and the Youth Research Foundation Project of Shanxi University of Finance and Economics(Grant No.QN-202015).
- Chinese Physics B的其它文章
- Robustness of community networks against cascading failures with heterogeneous redistribution strategies
- Identifying multiple influential spreaders in complex networks based on spectral graph theory
- Self-similarity of complex networks under centrality-based node removal strategy
- Percolation transitions in edge-coupled interdependent networks with directed dependency links
- Important edge identification in complex networks based on local and global features
- Free running period affected by network structures of suprachiasmatic nucleus neurons exposed to constant light

