Bo Song(宋波), Hui-Ming Wu(吳惠明), Yu-Rong Song(宋玉蓉),?, Guo-Ping Jiang(蔣國平),Ling-Ling Xia(夏玲玲), and Xu Wang(王旭)

1School of Modern Posts,Nanjing University of Post and Telecommunication,Nanjing 210023,China

2College of Automation&College of Artificial Intelligence,Nanjing University of Post and Telecommunication,Nanjing 210023,China

3Department of Computer Information and Cyber Security,Jiangsu Police Institute,Nanjing 210023,China

4GBDTC,University of Technology Sydney,Sydney,NSW 2007,Australia

Keywords: community networks,cascading failure model,network robustness,nodes influence identification

1.Introduction

Cascading failures have attracted considerable attention due to their widespread occurrence in various realworld systems and their highly destructive effect on network robustness.[1–5]Triggered by the failure of a single node or subsystem,the load of the failing node spreads to other nodes of the system, which in turn further increases the possibility of system failures, resulting in a vicious cycle or snowball effect.Cascading failures can bring the whole service down in a short space of time,and it will gradually deteriorate.In particular, the increasingly complex structures and functions of real-world systems are having a greater impact on the cascading failure process.[6–9]For example, the heterogeneity of nodes and communities in networks has an important impact on the whole cascading failure process,and node loadredistribution strategies based on node’s influence are continuously proposed.[3,4,10]Therefore,the impact of network structure on cascading failure has been one of the hot topics in research of complex network dynamics.

As a typical feature of complex systems, community attributes generally exist in various real systems,[11–16]such as social networks, energy networks and supply chain networks,[12–17]and have a strong impact on cascading failure processes.[18–20]Nakarmiet al.[18]studied the role of community structures in cascading failures in power grids.A centrality measure based on community structures is proposed to identify critical components of the system, and their protection can help in containing failures within a community and prevent the propagation of failures to large sections of the power grid.Panet al.[19]analyzed the vulnerability of a cyberphysical power system under community attack styles to study cascading failure.Wenet al.[20]proposed a new entropybased method combining the internal factors and external factors of community to measure the vulnerability of communities.These latest achievements have demonstrated the close interaction between community structure and cascading failure process.

Although the current research on cascading failures in community networks is relatively in-depth,it still faces many challenges as the structural and dynamic heterogeneity of real systems increases due to community structure.On the one hand, the influence of nodes becomes more granular as the importance,e.g.,size,connections,locations and functions of the communities to which they belong, varies.[21]Therefore,the initial load, load capacity setting and load redistribution strategy associated with node selection are also more heterogeneous due to the diversity of nodes and communities.On the other hand, the allocation problems between nodes in the cascading failure process are not only related to their influence,but also to whether they belong to the same community or even to the influence of different communities.For example, nodeiin communityAhas two neighbors with the same influence in two different communitiesAandB.Wheniis attacked and fails,it will preferentially select nodes in the same community for load balancing due to node similarity.It is not easy to take node similarity into account when measuring node influence,as the importance of similarity is not suitable for sorting.However, a load distribution strategy that preferentially selects nodes within or outside the community can be proposed to account for node similarity in the cascading failure model.

Therefore, node influence identification in community networks is the key point of studying network robustness against cascading failures, and the accurate measurement of node influence in community networks is the prerequisite for effective control of cascading failures.During the past decade,many node ranking methods have been proposed and improved to identify node influence, such as degree centrality (DC), betweenness centrality (BC), closeness centrality(CC),ClusterRanking(CR),PageRank and LeaderRank(LR)algorithms.[21–24]Due to the classification and clustering of nodes,[25]node influence identification in the community network is a very challenging task.First,the community structure makes the clustering of nodes more heterogeneous.Connections within communities are often closer than those between communities, and the heterogeneity of connections leads to greater differences in node status.For example, the relationships between nodes within the community are close, which makes the information difficult to break out as local clustering plays a negative role in diffusion.Secondly,even if two nodes have the same status in their respective communities,their importance in the network would be different due to different kinds of importance of the communities.

This paper presents a new cascading failure model based on node’s influence on community networks to analyze the impact of community structure on cascading failures.As a consequence of the new challenges,new derivations are necessary to extend the cascading failure model and evaluate the impact of community structure and node’s influence on the network robustness:

(i) A community-based Clustering–LeaderRank (CCL) algorithm for identifying node influence is proposed in this paper.Simulation results show that our algorithm can effectively identify the nodes with high influence in the community network under the premise of ensuring low computational complexity.

(ii) Based on the load-capacity model, a novel cascading failure model in a community network is proposed by considering the node and community influence.Heterogeneous load redistribution strategies are designed and analyzed.

(iii) Theoretical analysis and simulation on the robustness of community networks against cascading failures are carried out in this study, and the results show that network heterogeneity has a great impact on the cascading failure process.When the load share allocated to the same community neighbors becomes higher than that of the crosscommunity neighbors,the network shows better robustness.

The rest of this paper is organized as follows.In Section 2,we present the CCL algorithm proposed for node influence ranking.In Section 3,a novel cascading failure model in community networks is proposed,followed by the theoretical analysis of network robustness in different cases in Section 4.Numerical results are presented in Section 5,followed by conclusions in Section 6.

2.Community-based clustering-LeaderRank algorithm

Considering the local attributes,the connectivity of nodes and the influence of their community, a community-based clustering-LeaderRank (CCL) algorithm is proposed to identify influential nodes in community networks.Consider a networkG=(V,E), whereV={v1,v2,...,vN}represents node set andE={e1,e2,...,el}represents link set,Nandlare the numbers of nodes and links,respectively.The nodes inGare divided intom(2 ≤m ＜N) communities, where the nodes within the community are closely connected, while the links between the communities are sparse.The CCLi(t)of nodeiat timetcan be defined as

wherecjrepresents the clustering coefficient of nodejandf(cj)represents the function ofcj;f(cj)andcjare negatively correlated.IC(t) represents the influence of communityCat timet.Aij(t)is the adjacency matrix at timet,with the values being the weights between nodes,

Since the influence of a community is positively related to the influence of its internal nodes,IC(t) is defined as the sum of the influence of the internal nodes,

Here, an unweighted and bidirectional network withN=11 nodes andE=15 links is used to compare the effectiveness of the CCL algorithm proposed in this paper and some typical indicators to measure the influence of nodes.As shown in Fig.1,the network has been divided into two communities by the method in Ref.[26],where nodes I,J,K,and L are in the same community and other nodes are in another community.

Fig.1.A simple community network model.

The top 5 nodes according to the different methods are listed in Table 1.Using the CCL method, node A, which can be seen as a ‘bridge’ between two communities, has the highest influence.Both CCL and BC methods take into account the information transfer capacity of nodes in the network when measuring node influence.Nodes G and B are the second and third most important nodes in the CCL method due to the larger number of neighbors and the higher ranking of the community to which they belong.An interesting result is that in the CCL method,the influence of node B is higher than that of node I, while in the other methods it is the opposite.This is because,although the number of neighbors is the same,we can see from Fig.1 that the neighbors of node B have a higher influence than those of node I, and the community to which node B belongs is ranked higher than the one to which node I belongs.The results clearly show that our method integrates more comprehensive information.

Table 1.Top 5 nodes ranked by different methods in the network shown in Fig 1.

In order to further verify the effectiveness of our proposed method, two real networks with significant community characteristics are used in our paper.One is the widely used Dolphin social network, and the other is an aviation network we constructed.An aviation network is generated by intercepting the flights of 104 international airports distributed in different continents on 1 May 2022 from flightaware,[27]a global flight traffic query website.The nodes in the aviation network are international airports, and the links represent routes between the airports, while the number of routes is considered as the weight of the links.The basic information of the two networks is given in Table 2.

Table 2.Basic information of two networks.

In this way,we can draw graphs withNnodes andledges to describe the two networks.The adjacency matrix of graphGis{aij}.If there is a connection from nodeito nodej,aij=w,otherwiseaij=0.Using CCL and other classic node ranking methods,the influence of each node can be ranked and the effectiveness of different ranking methods can be analyzed by comparing the ranking results.

In addition,the susceptible-infected(SI)epidemic model is used in our paper to study the propagation influence of top nodes.[24,28,29]In the SI model, each node has two discrete states, susceptibleS(t) represents the number of individuals susceptible to the disease(not yet infected), and infectedI(t)denotes the number of individuals who have been infected and are able to spread the disease to susceptible individuals.At each step, for each infected node, a randomly susceptible neighbor is infected with probabilityγ(for uniformity,we setγ=aw/wmaxhere).For epidemic spread on networks,γdetermines the range or scale over which a node can exert influence.

Fig.2.Propagation processes in the Dolphin network with the top 5 nodes under different ranking methods as initial sources.

First,in the Dolphin network, the top 5 nodes under different node ranking methods are shown in Table 3.We can see that the ranking results of top 5 nodes under the CCL and CR methods are almost the same, and also very similar to the result of BC ranking methods.By using the SI epidemic model,with the top 5 nodes under different methods as the propagation sources, we show the propagation processes in Fig.2 under the same conditions.With the global information of the network, the performance of the BC method is the best.The performance of the CCL method is similar to that of the CR method,and is better than the LR method.

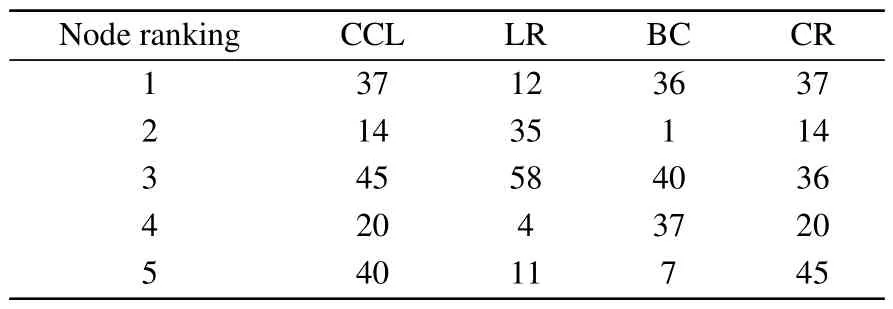
Table 3.Top 5 nodes in Dolphin network.

In Aviation network,we show the top 20 nodes under the CCL method through Table 4, and also give the ranking performance of these nodes under other ranking methods.The results in Table 4 show that the top 20 nodes ranked by the CCL method perform well in the other three ranking methods,especially in the LR and BC methods.

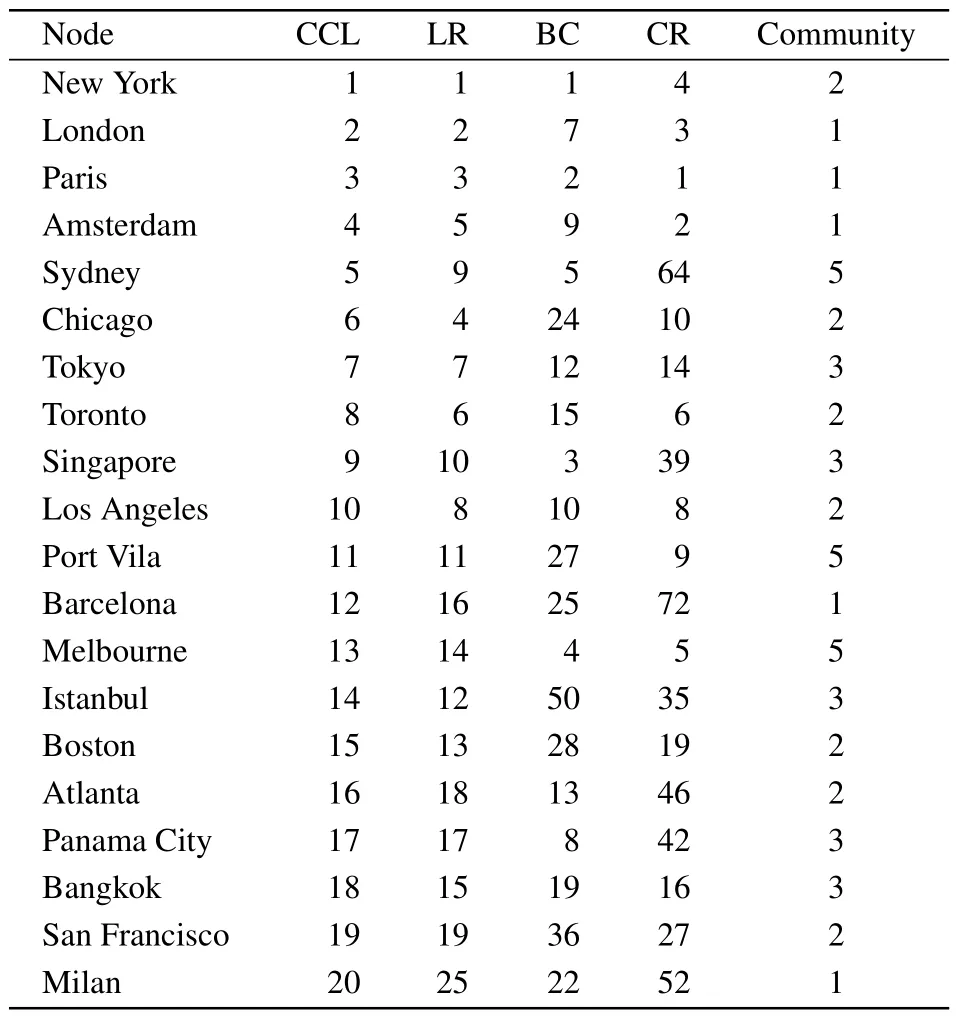
Table 4.Top 20 nodes ranking by different methods in the Aviation network.

Fig.3.The propagation process in the Aviation network with the top 5 nodes as a single infectious source, raked separately by the CCL method.

During verifying the effectiveness of our proposed CCL method,we also analyze and compare its time complexity.The BC method performs best on node’s ranking due to its global attribute based approach but with the highest time complexity ofO(N3),whereNis the number of nodes.The computational complexity of the proposed CCL and LeaderRank algorithm can be written asO(ml), wherelis the number of iterations when the CCL algorithm converges andmis the number of edges.The CR method owns the lowest computational complexity ofO(N), but the worst effects on node ranking in our simulations.

The LeaderRank algorithm has been proven to have excellent convergence as a ‘super node’ is introduced into the PageRank algorithm.Bidirectional edges between the super node and each node in the network make the network highly connected.[30]The clustering coefficient of nodes introduced in the CCL method is a constant and does not change with the increase of iteration times.Therefore,as an improved Leader-Rank algorithm, the CCL method can converges speedily.In our simulations,the CCL of each node will no longer change after 10 iterations.

The CCL method is used to rank nodes in two typical community networks, and the effectiveness of the CCL method is analyzed by comparing it with other typical node sorting methods.The results show that our method can effectively rank nodes in community networks.Furthermore, by using the SI propagation model, the role of the CCL method in identifying high-influence nodes is well verified.

3.A novel cascading failure model in community network

Consider a networkG= (V,E), whereV={v1,v2,...,vN}represents node set andE={e1,e2,...,em}represents link set,Nandmare the number of nodes and links,respectively.The nodes inGare divided inton(2 ≤n ＜N) communities, where the nodes within the community are closely connected, while the links between the communities are sparse.We assume that whenN →∞,the number of nodes in each community is equal.Thus,the probability that a node and its neighbor belong to the same community is 1/n.

At the initial stage,each node has an initial loadL(0)and a load capacityC.WhenL(0)＜C,the network is in a steady state.When a node fails, e.g., poor capital turnover of firms,bankruptcy, or product backlog, the load of the failed node is redistributed to its neighbors.If the load capacity of the neighbor is not sufficient to handle the additional loads, the neighbor would collapse.The dynamic process of redistribution continues until it disappears or all nodes fail.Assuming that the potential cascading failure is caused by the removal of a single node, we look at the cascading failure process of the network.Our model is briefly described as follows:

(1)Node initial load and load capacity The nodes’load and load capacity are generally related to the node influence,e.g., the position, the size, the scales.Therefore, the initial load of nodeiis defined as

whereIiis the influence of nodei,which can be measured by different methods,e.g.,different centralities,CCL method;αandλare the adjustable parameters that control the strength of the initial loads,α≥0 andλ≥0.The initial load of the node is proportional to its influence, which means that the nodes with higher influence can take more load.At the initial stage,the network is in a steady state,Li(0)is always lower than its load capabilityCi,as given by

whereβ(β＞0)is the tolerance parameter and suggests the upper bound of the ability that nodeiwithstands risks, i.e., the network shows stronger tolerance against cascading failures asβgrows.

(2)Heterogeneous load redistribution strategies First,the redistribution strategy is usually related to the node’s capacity, which can be described to some extent by structural properties such as degree, betweenness and closeness, which are used to measure the position of nodes and their relationship with other nodes in the network.Since node capability in our setting is directly proportional to node influence,we assign it according to node influence.

Taking into account the timeliness of the redistribution strategies and the updating of information,the probability that the failed nodeitransfers the load to its neighborjis given as

whereσis the parameter controlling the distribution share of cross-community nodes and intra-community nodes,0 ≤σ≤1.Whenσ ＞0.5, the share of load allocated to neighbors in the same municipality is higher than that of neighbors in different municipalities, and whenσ ＜0.5, the share of load allocated to neighbors in the same municipality is lower than that allocated to neighbors in different municipalities.Specially, whenσ=0.5, the probability of transmission,pi→j,has nothing to do with the community.Therefore, one of the key points of our research is the influence of the value ofσon cascading failure.At timet, the load distributed from nodeitojcan be written as

For the networkGwithNnodes andncommunities,the load of nodeichanges when its neighbor fails.Assuming the neighborjfailed at the initial time, then the load of nodeiat timeT=1 changes as

Cascading failure can be completely blocked if the load of any nodeiat timeT=1 is less than its load capacity,i.e.,

Based on the redistribution strategy in Eq.(7), the model should satisfy the following condition to ensure global robustness

As a special case,if the network has no community attribute,i.e.,n=1,Eq.(10)degenerates to

Based on Eq.(10), from the cascading failure condition formula considering the community structure,we can derive the network robustness against cascading failures under different cases.In particular, when the nodes in the network are uniformly mixed, such as in the ER network or regular network,we assume that the importance of each node is basically the same,i.e.,Ii=Ij,Eq.(10)can be rewritten as

Keeping the initial load distribution scheme and taking node initial load and load capacity in Eq.(12),we can reach

By a simple transformation, we can obtain the critical condition of node load capacity to ensure network robustness:

We introduce the critical threshold ofβ, denoted byβ*, to further discuss the robustness of different networks facing cascading failures.Whenβ≥β*,each node in the network is capable of handling additional loads so that there are no cascading failures and the system can continue to function as it used to.Otherwise, there are failed nodes in the network, which can lead to partial or even complete network failure, and the cascading failure occurs.Here,β*is the minimum value of the network’s ability to avoid global cascading failures.We can see from Eq.(13) that asσgrows,β*becomes smaller,and the network shows greater robustness against cascading failures.

4.Theoretical analysis on network robustness against cascading failures

In most cases, the network structure shows various heterogeneities, which lead to the different influences of nodes.Based on the influences, load redistribution strategies can be made to control cascading failures.Substituting Eqs.(1) and(2) into Eq.(10), we obtain the condition to ensure network robustness as follows:

After a simple adjustment,βshould satisfy

Assuming that the influence of the node is irrelevant,e.g.,the degree of nodes,as proved in Ref.[31],we can rewrite Eq.(15)as

The parameters show great impact on the load capacity thresholdβ*of cascading failure,whenθ=α,β*satisfies

whereIminandImaxare the minimum and maximum of node’s influence in the network,respectively.

Whenθ ＜α,the critical threshold satisfies

Whenθ ＞α,the critical threshold satisfies

From Eqs.(17)–(19) we can see thatβ*becomes smaller asσgrows.That is, when more loads are allocated to neighbors who are in the same community, the network becomes more robust against cascading failures under the heterogeneous load-redistribution strategies based on node influence.We can also derive the relationship betweenβ*and the loadredistribution parameterθby referring to Ref.[30].

Whenα ＜1,

Whenα ＞1,

Taking the more complex case further,i.e.,θ ＞αandα ＜1,we obtain

Whenθ ＜αandα ＞1,

5.Simulations

Numerical simulation results are provided to validate our proposed model and theoretical analysis in Section 4.First,we validate our model on 200 different BA networks.[32]Each network consists of 2000 nodes and the average degree is 6.The simulation results are the average of 200 simulation experiments in BA networks.As discussed in Section 4, whenθ=α,we can obtain the minimum ofβ*,i.e.,the network is most robust.Figure 4 shows the relations between robustness thresholdβ*andθ, with different values ofα.The simulation results in Fig.4 show intuitively that the value ofβ*is smallest whenθ=αin each case.It is also shown that whenθ=α=1,the value ofβ*is smallest in all 3 cases.

Furthermore,we also simulate and analyze the robustness with respect to load redistribution strategy on nodes in different communities or in the same community,i.e.,the impact ofσon the robustness thresholdβ*.Figure 5 showsβ*changing asθgrows under different values ofσ.With the sameθ,β*becomes smaller asσgrows, which means that, when the load proportion allocated to the same community neighbors becomes higher than that of the cross-community ones,the network shows better robustness.

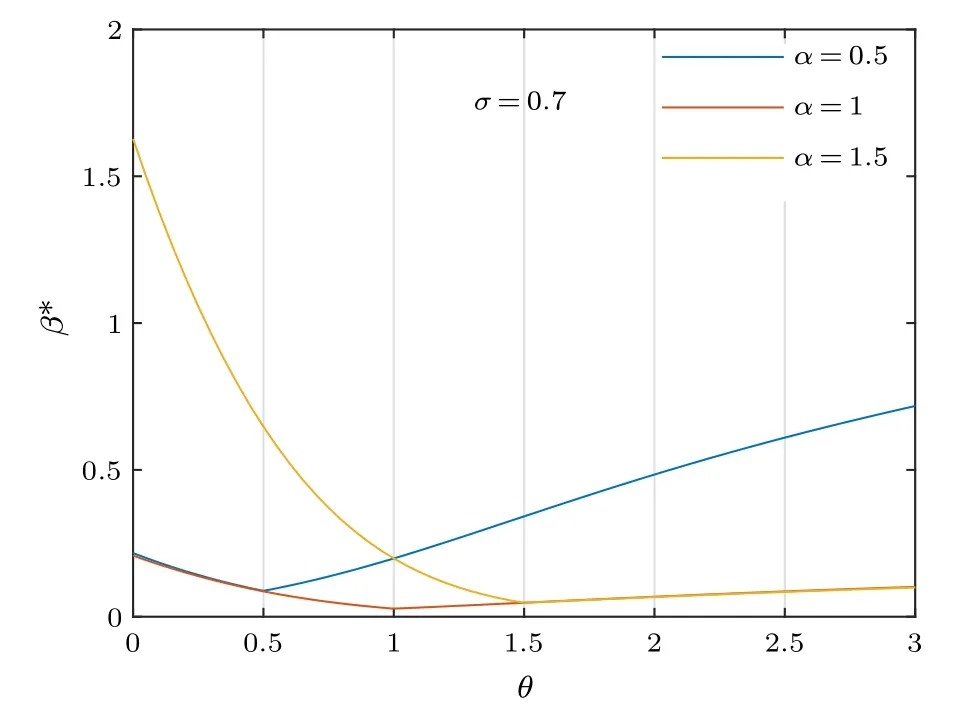
Fig.4.Relations between robustness threshold β* and θ with different values of α in BA networks.

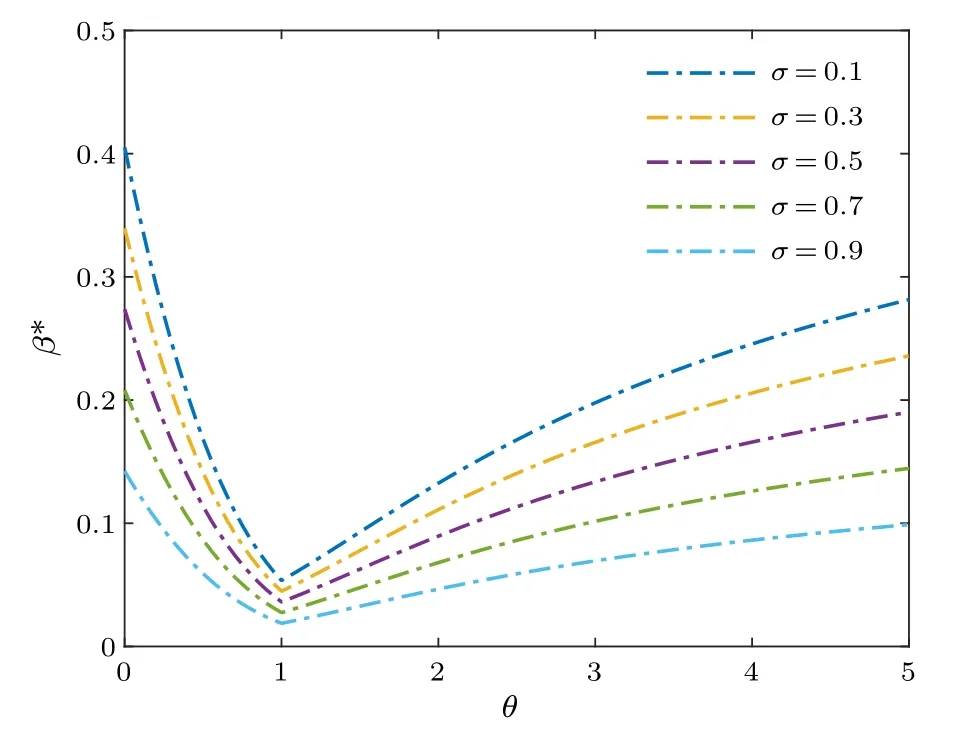
Fig.5.Relations between robustness threshold β* and θ with different values of σ in BA networks.

Fig.6.Relations between robustness threshold β* and θ with different values of α in the Dolphin social network(a)and the Aviation network(b).

In Section 2, the Dolphin social network and the Aviation network are used to verify the effectiveness of the CCL method on node ranking.Based on the node ranking results,here we proceed to perform numerical simulations on both the Dolphin social network and the Aviation network to analyze the network robustness against cascading failures, as shown in Fig.6.We can see that the value of critical thresholdβ*is smallest whenθ=αin both networks.Whenθ=1,the value ofβ*is smaller than the other 2 cases.

6.Discussion

In this paper, we focus on the robustness of community networks against cascading failures with heterogeneous redistribution strategies.First, an effective node influence ranking method, the CCL algorithm, is introduced and analyzed.Simulation results show that the CCL method can effectively identify the influence of nodes in community networks.Then,a novel cascading failure model based on node influence in community networks is proposed and the theoretical analysis on network robustness against cascading failures is carried out in our paper.The results show that the community attribute has an important influence on the cascading failure process.The network robustness against cascading failures increases when the load is more distributed to neighbors of the same community instead of different communities.When the initial load distribution and the load redistribution strategy based on the node influence in our paper are the same, the network shows better robustness against node failure.Simulation results show that keeping the transfer rate of load redistribution linearly proportional to the node influence leads to the strongest network robustness under the same conditions.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.62203229, 61672298,61873326, and 61802155), the Philosophy and Social Sciences Research of Universities in Jiangsu Province (Grant No.2018SJZDI142),the Natural Science Research Projects of Universities in Jiangsu Province (Grant No.20KJB120007),the Jiangsu Natural Science Foundation Youth Fund Project(Grant No.BK20200758), Qing Lan Project and the Science and Technology Project of Market Supervision Administration of Jiangsu Province(Grant No.KJ21125027).