Jian Zhou(周建), Changgui Gu(顧長(zhǎng)貴), Yuxuan Song(宋雨軒), and Yan Xu(許艷)

Business School,University of Shanghai for Science and Technology,Shanghai 200093,China

Keywords: circadian rhythm,light sensitivity,heterogeneous network,free running period

1.Introduction

Circadian rhythms are orchestrated by an endogenous biological clock which synchronizes the behavioral and physiological activities of living beings to the natural light-dark cycle.[1–4]Interestingly, even in the absence of an external light-dark cycle or environmental time cue, living beings can also sustain a robust rhythm with an endogenous period of approximation but not exact 24 h.[5–7]The endogenous period in constant condition,such as under constant light or under constant darkness, is called the free running period (FRP).[8–10]The length of the FRP varies under different conditions.[2,5]For example, the FRP length is smaller in the aging animals than the young animals under constant darkness,and the FRP length increases with the increase of the light intensity when exposed to constant light.[11,12]

In mammals, this endogenous clock is situated in the suprachiasmatic nucleus (SCN) in the anterior hypothalamus of the brain.[13]The SCN contains approximately 20000 selfoscillating neuronal oscillators with periods around 24 h.[14]The self-oscillating process of the SCN individual neurons is accomplished through a transcription-translation feedback loop composed of several key genes, such asPer,Cry,clock,andBmal1.[15]At the cellular level,the SCN neurons can display second-scale firing rhythms.The firing frequency of the SCN neurons is regulated by the genetic feedback loop.[16–18]In turn,the SCN neuron electrical activity affects the circadian oscillation properties of the genetic feedback loop, such as period, amplitude, and phase.[19–21]The interaction between electrical activity and feedback loop differs significantly from previous neuron models, such as the Hodgkin–Huxley model and the Mihalas–Niebur model.[22]The SCN neurons are nonidentical and express different intrinsic periods from the range of 22 h to 28 h.[2,6]The output of a robust rhythm with a uniform circadian period for these nonidentical neurons implies that the SCN neurons are well synchronized to form a network.[1,23,24]The cellular couplings play a key role in the synchronization,which are mainly through neurotransmitters,e.g., vasoactive intestinal polypeptide, arginine vasopressin,and gamma-aminobutyric acid.[25–27]

Although the exact topology of the SCN network has not been revealed, the SCN network is considered to be heterogenous.[28–30]Based on the heterogenous functions and network characteristic,it can be distinguished into two distinct subnetworks,including a ventrolateral(VL)part composed of about 25% SCN neurons and a dorsomedial (DM) part composed of rest SCN neurons.[31,32]The VL neurons are regarded as the hubs because the links of the VL neurons are much more than those of the DM neurons.[33–35]Additionally,the VL and the DM neurons have heterogenous characteristics in terms of the light sensitivity.[36–38]Early studies found that the VL neurons are directly sensitive to the light information originating from intrinsically photosensitive retinal ganglion cells through the retino-hypothalamic tract,and relay the information to the DM neurons.In contrast, the DM neurons are insensitive to the light information.[31,32,39]Recent studies found that both the VL and DM neurons are sensitive to light,but the sensitivity for the DM neurons are much smaller than that for the VL neurons.[36,37]Therefore, the sensitivity to light for the neurons and the number of links for the neurons are positively correlated.

In this article, we examine whether the FRP is affected by the SCN network structure based on a Poincaré model exposed to constant light.Four typical network structures are considered, including a nearest-neighbor coupled network, a Newman–Watts (NW) small world network,[40,41]an Erd¨os–Rényi(ER)random network,[42]and a Barab′asi–Albert(BA)scale free network.[43]The rest of this article is organized as follows.In Section 2,the Poincaré model is introduced to simulate an SCN network exposed to constant light.In Section 3,we present the simulation results of the effects of the SCN network structures on the FRP.In Section 4,the analytical results are presented.Finally, the conclusion and discussion are included in Section 5.

2.Description of the Poincaré model

In the field of circadian rhythms,two major types of models are predominantly used to describe the collective behavior of the SCN oscillatory networks, namely biochemical models, such as the Goodwin model,[44]and phenomenological models, such as the Kuramoto model[18]and the Poincaré model.[45–47]The Goodwin model describes the oscillator in terms of a genetic feedback loop,whereas the Poincaré model mimics the oscillator by a more general description.The results obtained from the latter are general enough to apply to synchronous rhythms generated by a single cell or coupled oscillators.[48]Furthermore,the analytical calculation of the Poincaré oscillator is straightforward.Thus, the Poincaré model,containing both phase and amplitude information,was utilized for numerical simulations and theoretical analysis.Each oscillator is modeled by two variablesxandy.The SCN network is coupled or linked through a local mean field of neurotransmitters.[49,50]Therefore,the model composed ofNoscillators exposed to the constant light reads

where the subscriptidenotes thei-th neuronal oscillator; the parametersγ,a, andτrepresent the relaxation parameter, intrinsic amplitude, and intrinsic period of the individual oscillator,respectively;μirepresents the dispersed intrinsic period for the individual oscillators which satisfies a normal distribution with the mean equal to 1 and the standard deviationσ.GFidescribes the local field term among the coupled neuronal oscillators,in which the parameterGrepresents the cellular coupling strength andFiis the local mean field.[34,48,51]The value ofFiis the mean value of the variablexover neighbors of theith node.The network structure of the SCN can be described by an adjacent matrixAN×N, whose elementAijis 1 when nodeiand nodejare connected, and otherwiseAij=0.Notably,the neuron oscillatoriis connected to itself here.The strength of circadian rhythms of the SCN network can be described by the synchronization degreeRof neuronal oscillators.The synchronization degreeRof the SCN neuronal oscillators can be expressed over time as follows:

The light termLiis equal toliL,whereLis the constant light intensity andliis the sensitivity of the SCN neurons to light information.Because the SCN neurons exhibit heterogeneity in light sensitivity, i.e., the VL neurons are much more sensitive to the light-information than the DM neurons,[36,37]and the links in VL neurons are denser than those in DM neurons.[34,35]Thus, there is positive correlation between the node degree and the sensitivity, we setli=di/D,i=1,2,...,N,withdidenoting the degree of nodei,i.e.,the number ofi’s neighbors.Dis the average node degree of the SCN network,which is equal toAccordingly,Ldi/Ddescribes the input of the light information depending on the node degree.

In the present study, we use the fourth-order Runge–Kutta method for the numerical simulations with time steps of 0.01 h.The initial 5×106steps(5×104h)are neglected to avoid the influence of transients and the next 1×105steps(1×103h) are selected.The initial values ofxandyare chosen randomly from a uniform distribution in the range(0,1) for each oscillator.Without special statement, we setγ=0.5,a=1,G=0.2,L=0.1, andτ=24,[32,48,52,53]and the standard deviation isσ=0, the total number of neurons isN=1000, and the each numerical simulation is averaged over 20 results to avoid the effects of randomness in network generations.

3.Numerical results

An illustrative example to examine the effect of the network topology of the SCN neurons on the FRP is shown in Fig.1,when exposed to constant light.In particular,the temporal evolutions of five randomly chosen oscillators are presented in the nearest-neighbor network (a), the NW network(b), the ER network (c), and the BA network (d).The value of the average node degree is selected to beD=10 for all the networks.The temporal evolutions of the five oscillators are highly synchronized and exhibit robust circadian rhythms in each panel(a)–(d), indicating that their periods are the same.The FRP is 27.97 h,28.31 h,28.59 h and 29.71 h,respectively,and the synchronization degree isR=1,0.99,0.97,and 0.88 for (a)–(d), respectivley.Therefore, the FRP in the BA network is longer than the other networks.Meanwhile,the value ofRis close to 1 within each panel, indicating that the SCN neurons are highly synchronized.R ≈1 agrees that thexvalues of the oscillators are almost equal within each network,i.e., the temporal evolutions of the SCN neuronal oscillators are almost identical within each network in Fig.1.

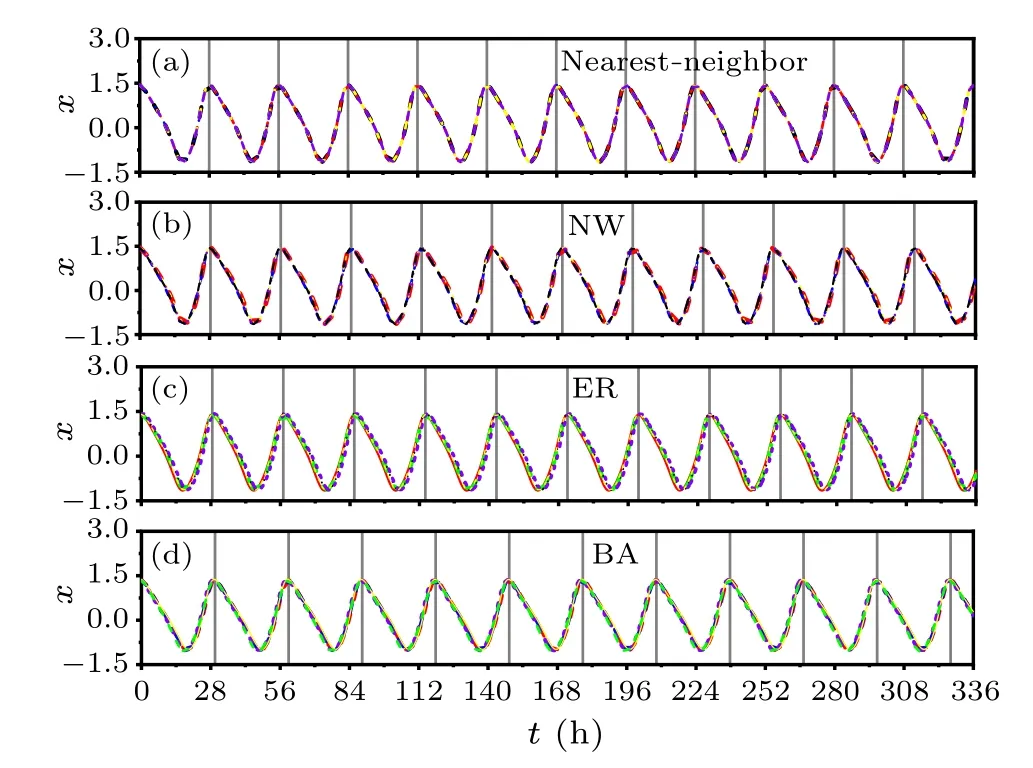
Fig.1.The temporal evolutions of the neuronal oscillators are affected by the SCN network structure under constant light.The evolutions of five oscillators are randomly chosen from the nearest-neighbor network(a),the NW network(b),the ER network(c),and the BA network(d).The average node degree is D=10 for all the networks.The peak of one randomly selected oscillator is indicated by a black solid line, accordingly,the length of the FRP is the interval between two consistent solid lines.

We next examine the effects of the SCN network structure on the FRP for the selected values of the average node degreeDin Fig.2.It is obvious that the relationship between the FRP andDdiffers in different networks,i.e.,the FRP is the longest in the BA network among the four networks for a focused value ofD.With the increase ofD,the FRP slightly decreases within each network.Figure 3 shows the relationships between the synchronization degreeRand the average node degreeDfor each network.The synchronization degreeRis around 0.9 in the BA network, and 1 in the nearest-neighbor network, the NW network or the ER network, whenDgoes from 10 to 50.Therefore, the neuronal oscillators are highly synchronized.Accordingly, the changes in the average node degree of the SCN network do not affect the main results that the FPR in the BA network is longer than that in the other three network structures.

Fig.2.Comparison of the relationship between FRP and average node degree D in four network structures, including nearest-neighbor, NW,ER,and BA networks. D is selected from 10 to 50.

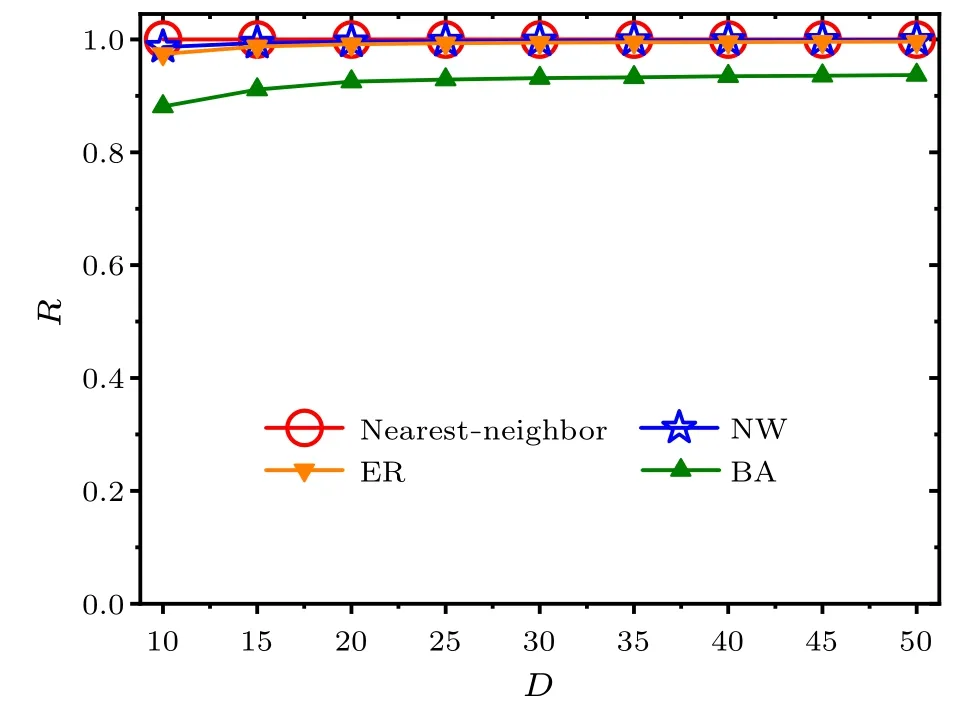
Fig.3.Relationships between the synchronization degree R and the average node degree D within each network. D is selected from 10 to 50.

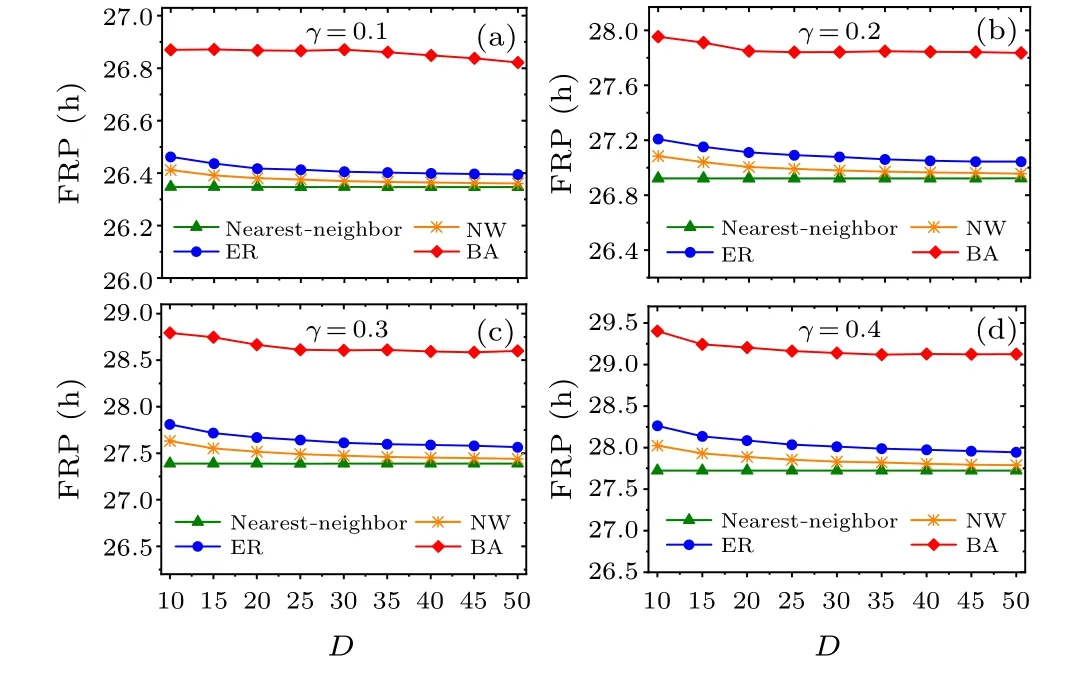
Fig.4.Comparison of the relationship between FRP and average node degree D.In panels (a)–(d), the relaxation rates γ is 0.1, 0.2, 0.3, and 0.4,respectively,and the range of D is taken from 10 to 50.

Moreover, we examine whether the main results are affected by the relaxation parameterγof the SCN neuronal oscillators(Figs.4 and 5).The four relaxation ratesγ=0.1,0.2,0.3, and 0.4 are examined in(a)–(d).Consistent with Figs.2 and 3, respectively, the FRP is longest in the BA network for each value ofγin Fig.4, and the synchronization degreeRis large for each network in Fig.5.Therefore,the changes in the relaxation rate of the SCN neuronal oscillators do not affect the main results,i.e.,the BA network has the longest FRP among the four networks.

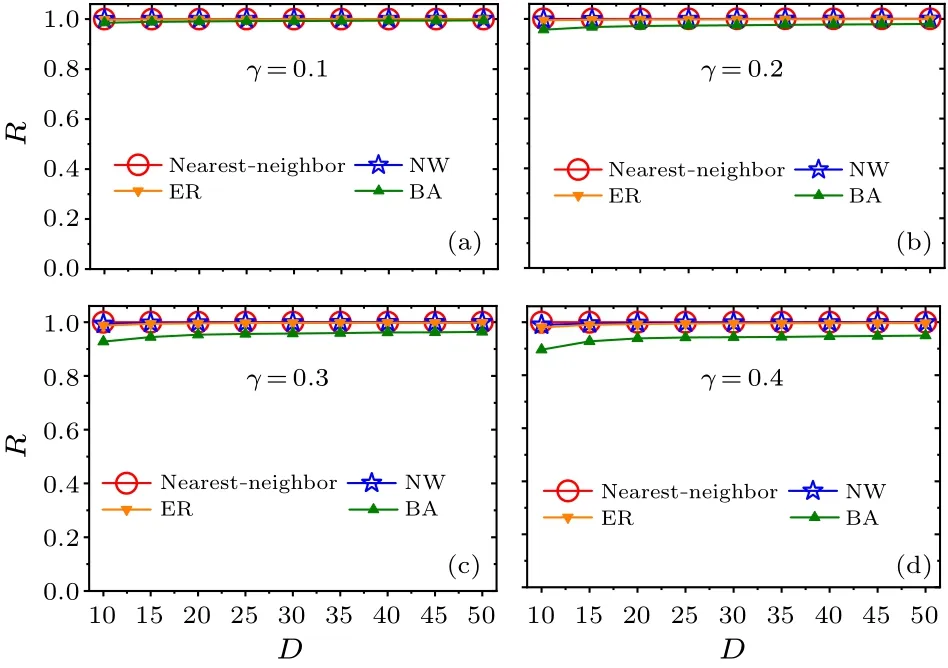
Fig.5.Relationships between the synchronization degree R and the average node degree D within each network for the four relaxation rates γ =0.1,0.2,0.3,and 0.4 in panels(a)–(d). D is selected from 10 to 50.Each value of R corresponds to each value of the FRP in Fig.4.

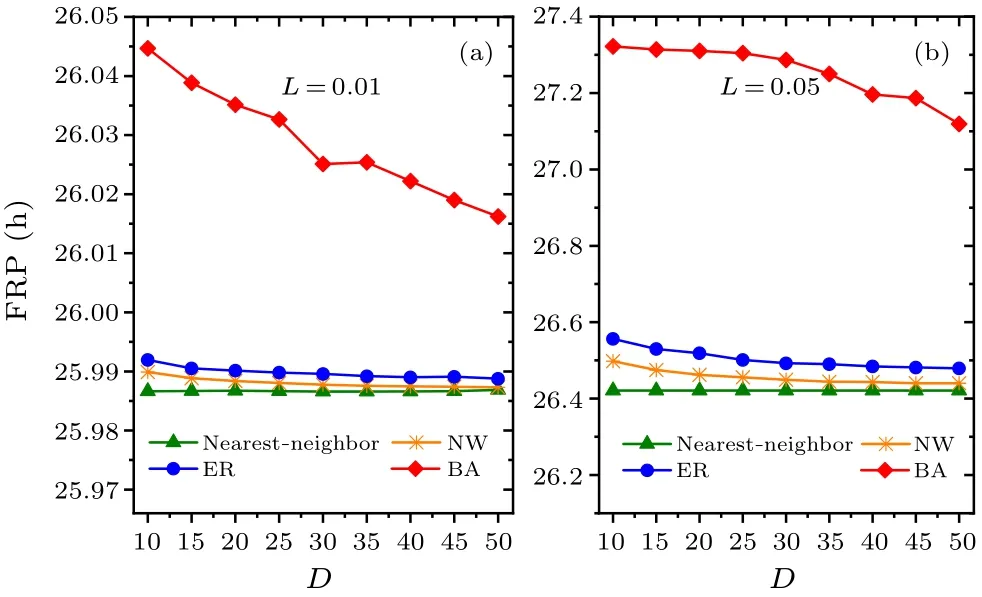
Fig.6.Comparison of the relationship between the FRP and the average node degree D.In panels(a)and(b),the intensities of constant light L are 0.01 and 0.05,respectively,and the range of D is 10–50.

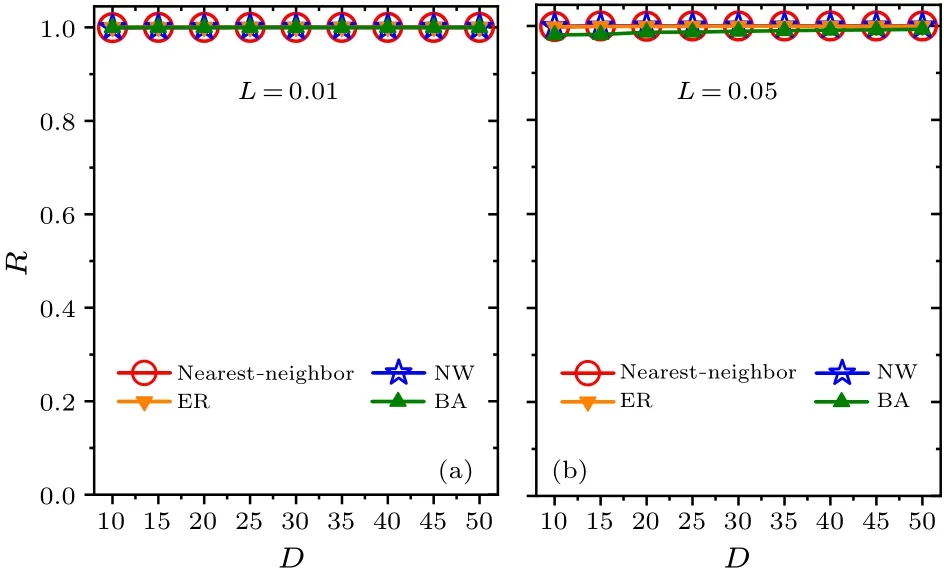
Fig.7.Relationships between the synchronization degree R and the average node degree D within each network for the two values of constant light intensity L=0.01 and 0.05 in panels(a)and(b), respectively. D is selected from 10 to 50.

In addition,we examine whether the intensity of constant light affects the main results (Figs.6 and 7).Two values of constant light intensityL=0.01 and 0.05 are examined in(a)and (b), respectively.Consistent with Figs.2 and 3, respectively,the FRP is longest in the BA network for each value ofLin Fig.6,and the synchronization degreeRis approximately equal to 1 for each network in Fig.7.Therefore,the changes in the intensity of constant light do not affect the main results,i.e., the FRP in the BA network is longer than the other networks.In comparison of Figs.2, 6 and 7, the FRP increases with the increase of the intensity of constant lightLfor a focused value ofDwithin each network.

4.Analytical results

In this section,we implement a series of theoretical analyses to explain the numerical results.The order of network heterogeneity going from the lowest to the highest is the nearestneighbor network,the NW network,the ER network,and the BA network.Accordingly,we use the most heterogeneous network topology, namely a star network, to mimic the BA network.In order to model the input of the light information of the SCN neurons depending on the node degree, for convenience,we consider the star network composed ofNnodes as the SCN network structure,[54,55]where the central node can be represented by oscillator 1, the leaf nodes are represented by the oscillators 2,3,4,...,N,respectively.

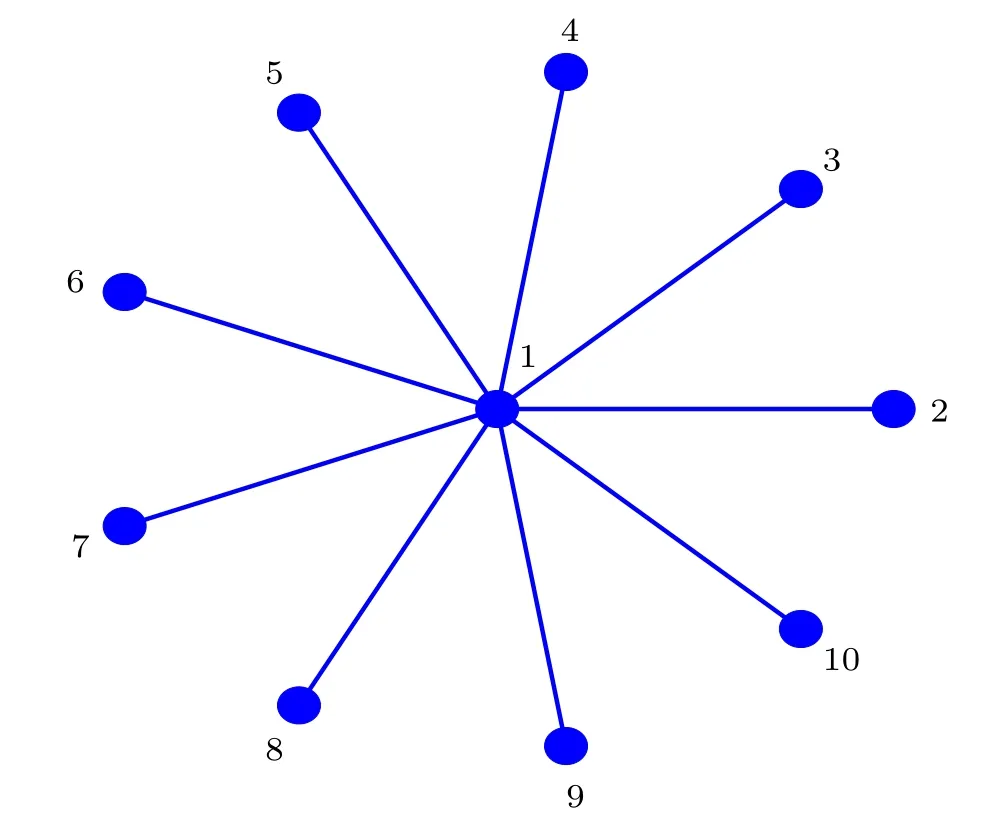
Fig.8.Schematic diagram of the star network composed of 10 nodes.

Figure 8 schematically shows the star network composed of 10 nodes.Since the leaf nodes in the star network are symmetrical,the system described by the Poincaré model reads

Here,ddenotes the degree of the central node,which is equal toN,and each leaf node degree is 2,because each node contains self-connected edge.The local mean fields of the neuronal oscillators 1 and 2 are expressed byand, respectively.Other parameters are the same as those in Eq.(1).Whendis small, the difference of degree between the central node and the leaf node is small,then the heterogeneity of the star network is low;whendis larger,this difference will be larger,and the heterogeneity of the star network will be higher.In addition,with the increase ofd,the central node has more links in the star network,i.e.,the central node is more sensitive to light.

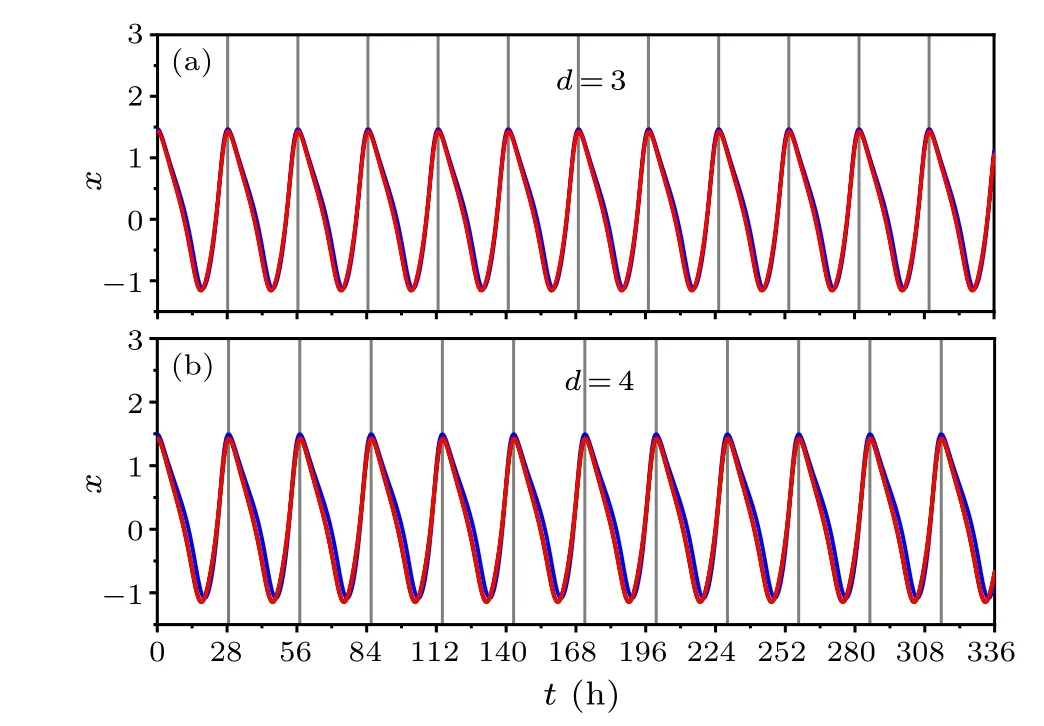
Fig.9.Temporal evolutions of the neuronal oscillators i affected by the star network structure under constant light:(a)d=3 and(b)d=4,i.e.,the sizes of the network are N=3 and N=4,respectively.The peak of one randomly selected oscillator is indicated by a black solid line,thus the FRP is the interval between two consistent solid lines.

Figure 9 shows the temporal evolutions of the SCN neurons affected by the star network under constant light.We taked=3 in panel(a)andd=4 in panel(b)as examples to present the results.The FRP is 28.17 h and 28.60 h in(a)and(b),respectively,and the synchronization degree isR=1 and 0.99 in(a)and(b),respectively.Therefore,the FRP ford=4 is longer than the FRP ford=3.It is seen that the temporal evolutions of the oscillators are highly synchronized and exhibit robust circadian rhythms in each panel of(a)and(b),indicating that the values of the oscillators are almost equal at the same time, and their periods are the same.Thus, we can obtainx1≈x2≈···≈xN,and the local mean field of the oscillator 1 is simplified to.Accordingly,Eq.(4)can be rewritten as

For theoretical analysis, Eq.(5) is transformed from Cartesian coordinates to polar coordinates.Letx1=r1cosθ1,y1=r1sinθ1,x2=r2cosθ2,y2=r2sinθ2, andω= 2π/τ.Substituting them into Eq.(5),consequently,we can obtain

When the SCN neuronal oscillators are synchronized,we have ˙r1= ˙r2=0, ˙θ1= ˙θ2=Ω,whereΩrepresents the angular frequency.Let the phases beθ1=Ωt+φ1andθ2=Ωt+φ2.The averaging method developed by Krylov and Bogoliubov as used in Refs.[32,48,53,56] is taken into account,φhas a lower time scale thanΩt.Letting the phase difference beα=φ2-φ1,then we have

where〈···〉 denotes the average in one circadian cycle.For simplicity, the non-averaged sign ofr1,r2,φ1, andφ2is kept in the rest of the article.Substituting Eq.(7)into Eq.(6), we obtain

From Eq.(8),we acquire

Due to sin2θ1+cos2θ1= 1 and sin2θ2+cos2θ2= 1,Eq.(9)can reduce to

When all the oscillators are in a synchronized state,Fig.9 shows that the amplitudes of the SCN neurons are almost equal(B ≡r1≈r2).From Eq.(10),consequently,we have

When the oscillators output one uniform FRP,i.e.,the oscillators are synchronized,the difference between the oscillators is very small in that we obtainα →0 and cosα →1.After substituting Eq.(11)into Eq.(10),we obtain

wherec ≡(1/2)B(a-B)+(GB/2).

Therefore,Ωcan be solved from Eq.(12)as

From Eq.(13), we observe that the relationship betweenΩanddis negative, i.e., between the FRP anddis positive.Moreover,the larger the central node degreedin the star network is,the larger difference between the central node degree and the leaf node degree is,indicating that the heterogeneity of the star network is large.Therefore,the larger the heterogeneity of the network is, the longer the FRP is.In other words,the FRP of the neuronal oscillator increases with the increase ofd,when the oscillators are synchronized.It shows that the results of the FRP affected by network heterogeneity are consistent with our numerical simulations, i.e., the BA network has the longest FRP because its network structure is most heterogeneous.Consequently,we theoretically explain the results in Fig.1.Moreover, the relationship of the FRP or the synchronization degreeRto the central node degreedin the star network is shown in Fig.10, and the numerical simulations from Eq.(4).It indicates that the neuronal oscillators are in perfect synchronicity (R ＞0.95) and that the FRP increases with the increase ofd.

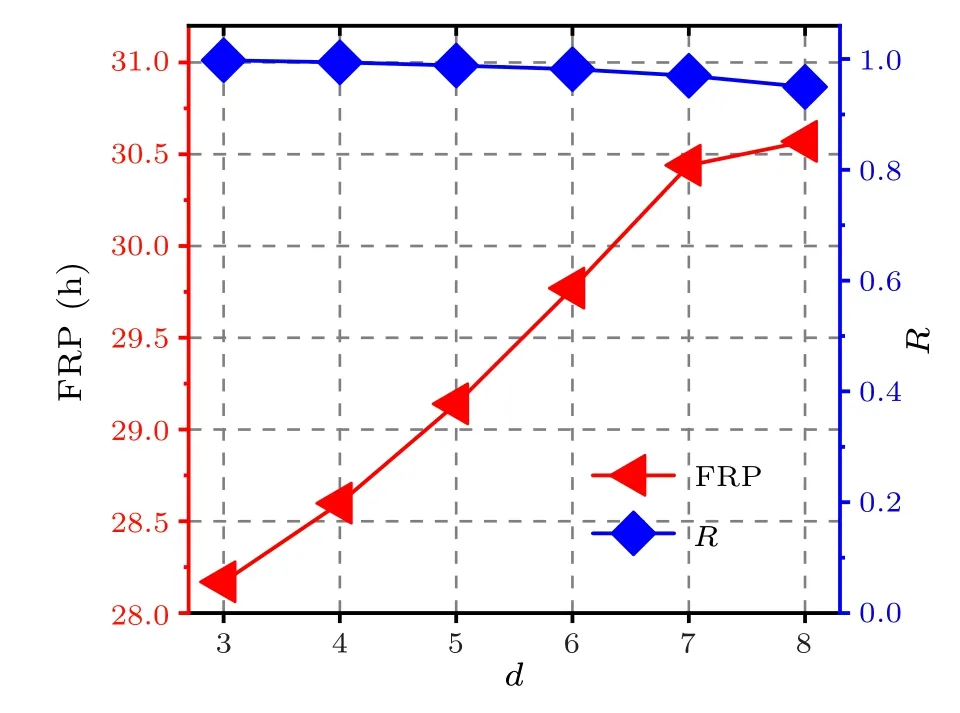
Fig.10.The relationship of the FRP or the synchronization degree R to the central node degree d in the star network.

5.Discussion and conclusion

In summary,we have investigated the effects of the SCN network structure on the FRP length based on the Poincaré model exposed to constant light.Although the precise network structure is currently unclear,the SCN network structure is thought to be heterogeneous.[28–30]The VL neurons have more links than the DM neurons.In addition, the sensitivity to the light information is heterogenous for the SCN neurons,i.e., the VL neurons are more sensitive to the light than the DM neurons.[36–38]Thus far,it is unknown how the SCN network structure affects the FRP.In this study,four typical networks are considered, namely the nearest-neighbor network(most homogeneous network), the NW small world network,the ER random network,and the BA scale-free network(most heterogeneous network).We find that the FRP in the BA network is longer than the other three networks.

Aschoff’s rule suggests that different animals have different FRPs under constant-light conditions.[8,57]A possible reason given in this article is that the SCN network of the animals with longer FRP has more hub nodes(e.g.,BA scale-free network), which are more sensitive to light.In contrast, the SCN network of the animals with shorter FRP has fewer or even no hub nodes(e.g.,nearest-neighbor network),which are less sensitive to light.

In addition, previous studies have demonstrated that the FRP of one animal varies in response to different photoperiods(seasons)or age.[46,58]For instance,compared with other age groups, adolescents tend to have a longer chronotype, which means that they have a longer FRP.[58]This temporal change may also be related to the change in the light sensitive heterogeneity of the SCN neurons,caused by these different photoperiods (seasons) or age, thus resulting in a change in the neuronal endogenous periods.Our work not only contributes to understanding the mechanisms by which the SCN neurons are sensitive to light information, but also provides a potential explanation to understand that different animals or an animal exhibits different rhythmic behaviors under constant-light conditions.

In fact,there are other neuronal models.For instance,Xuet al.summarized the development process since the establishment of the first neuron model in 1907, and summarized 17 most representative mathematical models.They were divided into conductance-dependent models and non-conductancedependent models for comparative analysis.Moreover, Xuet al.highlighted five classical models including the neuron on the latest neural chip TrueNorth, and analyzed their simulation characteristics and the requirements for circuit implementation.[22]The electrical activities of neuronal models include the Hodgkin–Huxley model, and Mihalas–Niebur model,etc.,which are basically on the millisecond or second scale.The SCN neuron is a special kind of neurons.Its electrical activity can not only exhibit firing rhythms at the second scale,but also reveal circadian rhythmic behavior at the circadian scale.These two rhythms interplay with each other.In detail, the firing frequency of the SCN neurons is modulated by the genetic feedback loops.In turn, the electrical activity of the SCN neurons affects the nature of the circadian oscillations of the genetic feedback loop.In this article,the collective behavior of the SCN neuron oscillators is explored at the circadian scale.In-depth exploration of the interactions between the SCN neurons at the second and circadian scales is our future research focus.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.12275179 and 11875042)and the Natural Science Foundation of Shanghai (Grant No.21ZR1443900).