All-electron ZORA triple zeta basis sets for the elements Cs–La and Hf–Rn
Ant?nio Canal Neto, Francisco E.Jorge, and Henrique R.C.da Cruz
Departamento de F′?sica,Universidade Federal do Esp′?rito Santo,29075-910 Vit′oria,ES,Brazil
Keywords: TZP-ZORA and ATZP-ZORA basis sets, ZORA-B3LYP method, Cs–La and Hf–Rn elements,atomic and molecular properties
1.Introduction
Some theoretical problems naturally arise when working with elements of the fifth row, specifically, the correlation of electrons and relativistic effects must be simultaneously treated in a system of several electrons.[1]In order to reduce the computation time, some approximations have often been proposed and adopted in the literature.Among them,one can highlight the relativistic effective core potential(ECP),where the number of electrons to be handled is significantly reduced,since only the electrons of valence or those of the outermost shell were explicitly considered in the calculations.For instance, the ECP model has successfully been used mainly in predicting bond lengths and relative energy.[2]However, this approach has received some criticisms.[3–5]In addition,it has its own limitations when it is used to determine physical properties involving electrons from the inner shells, such as paramagnetic resonance,topological analysis of electron densities,and M¨ossbauer and x-ray absorption spectra.Especially for these latter cases,it is necessary to have relativistic all-electron basis sets that are compact and accurate.
As Dirac’s Hamiltonian naturally incorporates all relativistic effects, it would be ideal for performing such calculations.However,the four-component wave functions,generated from the Dirac’s Hamiltonian, make their performances almost prohibitive for medium- or large-sized molecules.To make these wave functions simpler,some approximations have been used to estimate the scalar relativistic effects.Among them, we will mention two of most relevant approximations,that is,the zero-order regular approximation(ZORA)[6]of the Dirac Hamiltonian and the Douglas–Kroll–Hess (DKH) unitary transformation.[7–9]The spin–orbit effect has often been estimated through perturbation theory.
In this work,another question that arises is which method we must use to perform the calculations.It is known from the literature that theab initiomethods, in general, are accurate,but they require longer computation time than, for instance,the density functional theory(DFT).The latter is usually less accurate, but it still considers the correlation of electrons.In the case of systems containing few electrons,one can use anyab initiomethod or DFT,but if the number of electrons is too big,the calculations are restricted to DFT.
Since 2009,our research group has generated all-electron relativistic basis sets for the elements H–La and Hf–Rn.One of our main concerns was to have basis sets as compact as possible, but these sets should still remain accurate and reliable to be used either in DFT or inab initiocalculations of electronic structures of atoms, molecules, and clusters.Among the basis sets developed in our group, we must mention the segmented basis set of triple zeta valence quality plus polarization functions(TZP)to be used together with the DKH Hamiltonian.It has been designated as TZP-DKH.[10–12]Several search groups have successfully used the above mentioned basis set(see,e.g.,Refs.[13–21]).
For the elements of the fifth row,one can find in the literature some all-electron basis sets[22–28]specifically optimized for the second-or third-order DKH(DKH2 or DKH3)Hamiltonians.For these elements, though the number of basis sets optimized by ZORA Hamiltonian is reduced, the number of programs(ADF,DIRAC,NWChem,ORCA,etc.),that makes this Hamiltonian available, is not small.Because the implementation of the ZORA Hamiltonian in the NWChem program is different from that of ORCA program,a big precaution should be taken when using basis sets specially generated for the latter code in NWChem.In the ADF program,ZORA basis sets, developed from Slater-type functions, are available.However, as is well known, most of quantum chemistry programs have been prepared to handle Gaussian-type functions(GTFs).For Hf–Hg, a family of all-electron Gaussian basis sets, to be employed together with ZORA Hamiltonian, was presented by Pantaziset al.[28]With the purpose of spending less computational time on molecular calculations, Centoducatteet al.[29]developed the DZP-ZORA and ADZP-ZORA all-electron Gaussian basis sets for all elements of the fifth row.Therefore,the main objective of this work is to generate triple zeta basis set to reduce the basis set truncation error.
Recently,we developed the TZP-ZORA basis set for the elements from H to Xe.[30]As it has been mentioned earlier,the aim of this work is to extend this set based on the proposal of encompassing the elements Cs–La and Hf–Rn.For each orbital angular momentum,a diffuse function is added to give rise to the basis set called augmented TZP-ZORA(ATZPZORA).This set is suitable for describing electrons distant from atomic nuclei.Using the TZP-ZORA set and ATZPZORA set in combination with the ZORA-B3LYP method,the values of ionization energy(Ei)and static mean dipole polarizability(ˉα)of some atoms and bond length(re),dissociation energy(De),and harmonic vibrational frequency(ωe)of some diatomic molecules are calculated.These results are then compared with the theoretical and experimental data previously published in the literature.The performances of the ZORA and DKH2 Hamiltonians are also evaluated.
2.Generation of relativistic basis sets
The same procedure applied to H–Xe[30]was used to generate the TZP-ZORA basis set for the Cs–La and Hf–Rn elements.For each atom,we started with the TZP non-relativistic set[12]and then we reoptimized the contraction coefficients of orbital angular momentum s,p,d,and f,always with the minimum ZORA-ROHF (restricted open-shell HF) energy criterion considered.In this process, the ground states of atoms[Cs(2S),Ba(1S),La(2D),Hf(3F),Ta(4F),W(5D),Re(6S),Os(5D),Ir(4F),Pt(3D),Au(2S),Hg(1S),Tl(2P),Pb(3P),Bi(4S),Po(3P),At(2P),and Rn(1S)]were considered and also,the method of optimizing nonlinear parameters, proposed by Jorge and Canal Neto[31]and the ORCA 4.0 program[32]were employed.We used the nuclear model of point charges because it is the only approach available in the ORCA code for the ZORA Hamiltonian.It is worth noticing that only contraction coefficients have been reoptimized, while the GTF exponents and contraction schemes have remained the same as those in the original TZP basis set.Pantaziset al.[28]used a similar procedure in the generation of SARC-ZORA sets for Hf–Hg,i.e., they have only reoptimized the contraction coefficients of a non-relativistic basis set.
Here, the generation of the primitive Gaussian functions of the non-relativistic TZP basis set was described briefly.[12]Once again,the optimization method,developed in Ref.[31],was used to generate these functions.Even for heavy elements in the periodic table, we have shown that the differences between the Hartree–Fock(HF)energy obtained with the uncontracted TZP set, and the corresponding HF numerical results are small,for example,for Fr,Ra,and Ac this difference is less than 1 Hartree(1 Hartree=2 Ry=27.2114 eV).[33]This finding indicates that the orbital angular momenta s and p of our non-relativistic basis set have narrow functions.It can also be verified by calculating the ZORA-ROHF energy values with the uncontracted TZP and ANO-RCC-VQZP[23]sets.For Rn,which is the heaviest element studied in this work,the difference between the energy values computed with these two basis sets is only 1.621175 Hartree.
For heavy atoms, the radial behavior of the nonrelativistic wave function significantly differs from the relativistic wave function,since there are contractions and expansions of the atomic orbitals of the inner and outer shells,[34]respectively.This means that the use of non-relativistic basis sets in relativistic calculations can give rise to undesirable results of molecular properties.[34]Canal Netoet al.[30]found that the mixing of a DKH basis set with the ZORA Hamiltonian may also be responsible for disastrous atomic and molecular results.These observations together with those discussed above were what motivated us to construct for the elements of the fifth row specific Gaussian basis sets to perform ZORA calculations.
There is a set of properties(polarizabilities,electron affinity, electronic circular dichroism, optical rotation, and hydrogen bonds)that depends on a good description of the electrons far from the nuclei.To do this, we add a diffuse function to each of orbital angular momenta s, p, d, and f of our TZPZORA basis set.These functions,which were directly picked up from our ATZP non-relativistic basis set for Cs–La and Hf–Rn,[12]gave rise to the ATZP-ZORA set.For each element of the fifth row,in Table 1 are listed the numbers of GTFs for each orbital angular momentum of the uncontracted and contracted TZP-ZORA and ATZP-ZORA sets.It can be noticed that no diffuse functions were added to some orbital angular momenta of some atoms of the ATZP-ZORA set.The reason is that the corresponding orbital angular momenta of the TZP-ZORA set already have had the functions with these characteristics.

Table 1.Details of TZP-ZORA basis set and ATZP-ZORA basis set for Cs,Ba,La,and Hf–Rn.
3.Results and discussion
All calculations are performed by using the ZORAB3LYP method available in ORCA 4.0 code.[32]Dissociation energy and harmonic vibrational frequency are computed from the optimized geometries of diatomic molecules.
3.1.Ionization energy
For some elements of the fifth row, the values of ionization energy, computed with the ZORA-B3LYP/TZP-ZORA,DKH2-B3LYP/TZP-DKH,ZORA-B3LYP/ATZP-ZORA,and ZORA-B3LYP/ANO-RCC-VQZP-unc theoretical procedures,are shown in Table 2.Experimental data[35]are also included.The uncontracted basis sets [(26s,22p,15d,4f,2g)for Cs and Ba, (24s,21p,15d,11f,4g,2h) for Hf–Hg, and(25s,22p,16d,12f,4g) for Tl–Rn] developed by Rooset al.[22–24]are represented by the ANO-RCC-VQZP-unc abbreviation.Owing to its performance in calculating atomic and molecular properties and its large size, the results of this set can be used to estimate the truncation error of smaller basis sets(cf.,Refs.[22–24,29,36]and references therein).
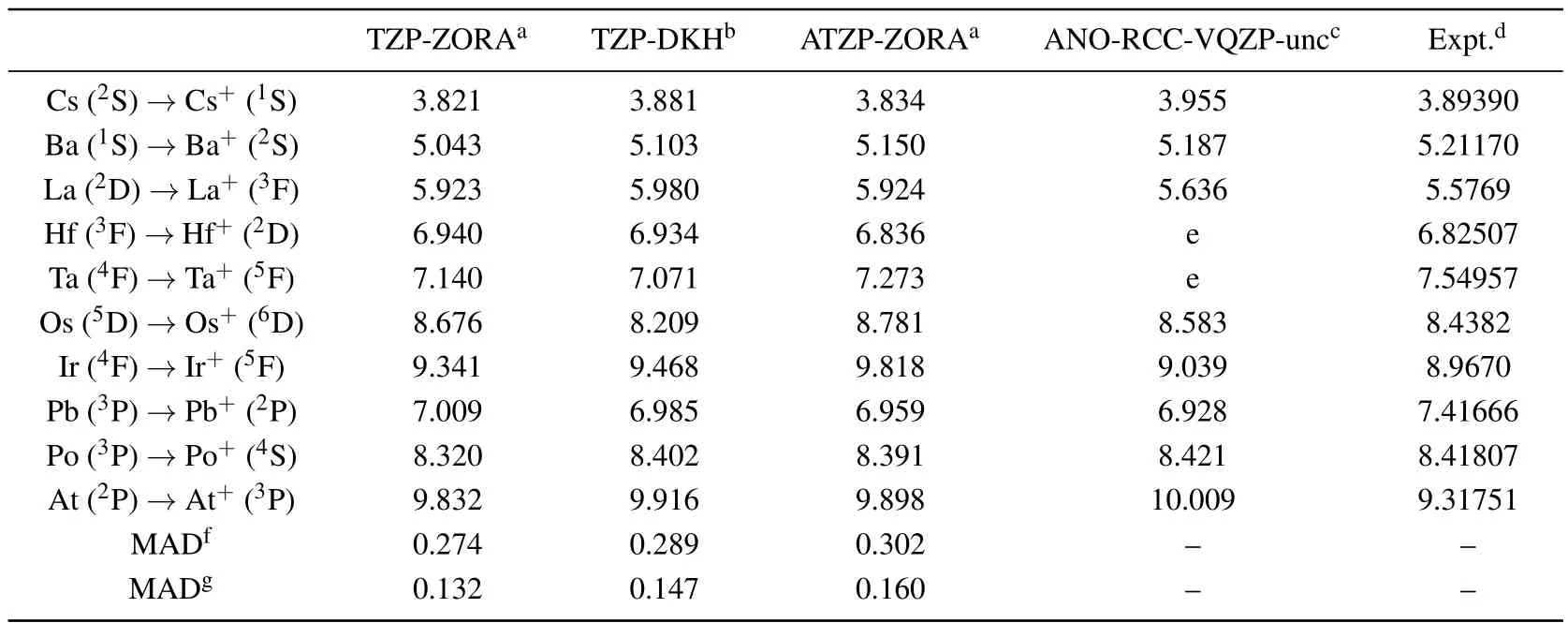
Table 2.Theoretical and experimental ionization energy values(in unit eV)of some elements.
All theoretical and experimental results,listed in Table 2,increase from Cs to La,from Hf to Ir,and from Pb to At.Except for Os,all other ZORA-B3LYP/TZP-ZORA and DKH2-B3LYP/TZP-DKH ionization energies are very close to each other.Even for Os, the performances of the two theoretical models prove to be equivalent, since their results are approximately equidistant from the experimental value.Overall,the mean absolute deviations(MADs)of the ZORA-B3LYP/TZPZORA and DKH2-B3LYP/TZP-DKH ionization energy relative to the ZORA-B3LYP/ANO-RCC-VQZP-unc and experimental values are 0.274 and 0.132 and 0.289 and 0.147 eV(see Table 2),respectively.These values clearly show that the precisions,obtained with both theoretical models,are approximately equal and also gives us confidence to test the performance of the TZP-ZORA set in estimating other properties of the systems.Considering the ATZP-ZORA set, MADs increase to 0.302 eV and 0.160 eV, respectively.These values clearly demonstrate that the addition of diffuse functions to the TZP-ZORA set will not improve the values of ionization energy.
Before closing this Section, the energy values of some occupied atomic orbitals of the Hf are briefly discussed.For orbitals 1s, 2s, 2p, 3s, and 3p of the inner shells, the energy values,obtained with the all-electron basis sets,are very close to each other(see Table 3).For the outer shell orbitals,the corresponding values of orbital energy,calculated with the TZPZORA, TZP-uncontracted, and ANO-RCC-VQZP-unc sets,are not very different from each other.All theoretical models predict that the highest energy orbital is 5d followed by 6s,which is in line with predictions made by the NIST Atomic Spectra Database.[35]
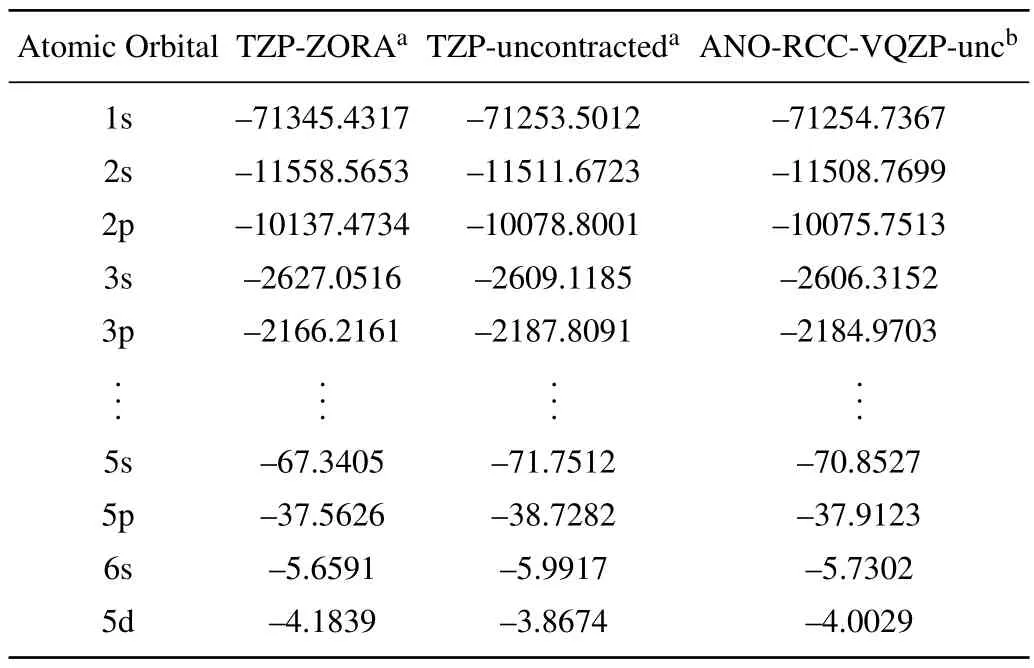
Table 3.Energy values(in unit eV)from some atomic orbitals of Hafnium in ground state.
3.2.Polarizability
The mean dipole polarizability is associated with deformation suffered by the electron cloud when it radiates through an electric field.This is a good test for the ATZP-ZORA set,because this property is sensitive to the theoretical procedure employed to determine it.
Table 4 displays the mean dipole polarizabilities of some elements obtained by the ZORA-B3LYP method together with the TZP-ZORA and ATZP-ZORA basis sets.To evaluate the quality of these results,benchmark theoretical values,[29]recommended and experimental data[37]are also included.
From Table 4, it can be noticed that all TZP-ZORA mean dipole polarizabilities are underestimated when compared with the recommended and experimental values[37]as well as with the benchmark theoretical results.[29]For example, for Ir and Pt, TZP-ZORA polarizabilities are approximately ten times lower than the corresponding values reported in Ref.[37].The main reason for such discrepancies is because the TZP-ZORA set does not have diffuse functions to describe the most distant electrons from the atomic nuclei.In contrast, going from TZP-ZORA to ATZP-ZORA,the polarizabilities of all studied elements significantly increase.Now, with the exception of a few cases, all other ZORA-B3LYP/ATZP-ZORA static mean dipole polarizabilities are always between the uncertainty bars of the recommended values and experimental value.[37]Among the exceptions, Ir and Tl stand out, however, their mean dipole polarizabilities are in excellent agreement with the benchmark theoretical values[29](see Table 4).Overall, the MAD value of the ZORA-B3LYP/ATZP-ZORA results relative to the ZORA-B3LYP/ANO-RCC-VQZP-unc polarizabilities is low(3.839 a.u.),indicating not only the good performance of this set on polarizability calculations,but it also a good expectation if it can be used to estimate other properties that depend on an appropriate description of electrons distant from nuclei.It is worth noticing that the TZP-ZORA MAD of 41.281 a.u.is much larger than the latter.

Table 4.Static mean dipole polarizabilities for ground states of some elements.All values are in units of atomic unit(a.u.).
3.3.Bond length
Theoretical and experimental results[38–42]of bond lengths, harmonic vibrational frequencies, and dissociation energies of fifteen diatomic molecules containing elements of the fifth row are shown in Table 5.It shows some general trends.Dimers of alkaline and alkali earth are known to form long chemical bonds.The bond lengths of Cs2and Ba2are the largest as shown in Table 5.In the ground state,the 6s valence orbitals of Ba and Cs are doubly and singly occupied,respectively.This observation justifies the bond length of Ba2being longer than that of Cs2.Going from Cs2to CsH and from Ba2to BaH, all theoretical and experimental results show a significant reduction of bond lengths.These results are already expected,since the valence orbitals of Cs and Ba and H are 6s and 1s orbitals,respectively.From Ba2to La2expected is another reduction in the bond length,since the 5d valence orbital of La belongs to an inner shell.Chemical intuition also predicts a reduction in bond length through the Tl2→TlI→TlCl series, since the valence orbitals of Tl, I, and Cl are 6p, 5p,and 3p,respectively.This prediction is confirmed through the ZORA-B3LYP/TZP-ZORA and ATZP-ZORA results that appear in Table 5.A similar analysis also justifies the reduction of ZORA-B3LYP/TZP-ZORA and ATZP-ZORA and experimental bond lengths through the Pb2→PbSe→PbO series.
Except for Ba2and Tl2, all other ZORA-B3LYP/TZPZORA and DKH2-B3LYP/TZP-DKH corresponding bond lengths are very close to each other.For Ba2, we did not find any experimental value in the previous literature.The ZORA-B3LYP/TZP-ZORA result is closer to the bond length of 5.100 ?A[24]obtained by the DKHCASSCF/CASPT2/[12s10p8d4f] (a highly accurate method in conjunction with an all-electron basis set) than that calculated from the DKH2-B3LYP/TZP-DKH theoretical model.For Tl2, there are two experimental values of 3.02 ?A[41]and 2.75 ?A[42]reported in the literature, which accord very well with the ZORA-B3LYP/TZP-ZORA and DKH2-B3LYP/TZPDKH bond lengths, respectively.A value of 3.025 ?A,[43]which is very close to the ZORA-B3LYP/TZP-ZORA result,is determined by Roos and Malmqvist through using the DKHCASSCF/CASPT2/ANO-RCC-QZP procedure.
Not only with the ZORA-B3LYP/ANO-RCC-VQZP-unc benchmark theoretical values computed in Ref.[29] do the ZORA-B3LYP/TZP-ZORA bond lengths accord with,but also with other theoretical results found in the literature[24,43–48](see Table 5).The only exception occurs for Pt2, where the B3LYP/LANL2DZ value is 2.47 ?A,[44]while our result is quite close to the experimental value of 2.33 ?A.Compared with the experimental bond lengths found in the literature,[38–42]the ZORA-B3LYP/TZP-ZORA results also agree very well.Overall, the MADs of the theoretical values ZORA-B3LYP/TZP-ZORA and DKH2-B3LYP/TZPDKH relative to the experimental data are low (0.032 ?A and 0.036 ?A, respectively).When ZORA-B3LYP/ATZP-ZORA results are considered, the MAD will be 0.089 ?A, an almost threefold increase.

Table 5.Theoretical and experimental bond lengths(re in unit ?A),harmonic vibrational frequencies(ωe in unit cm-1),and dissociation energies(De in unit eV)of some molecules in the ground state.
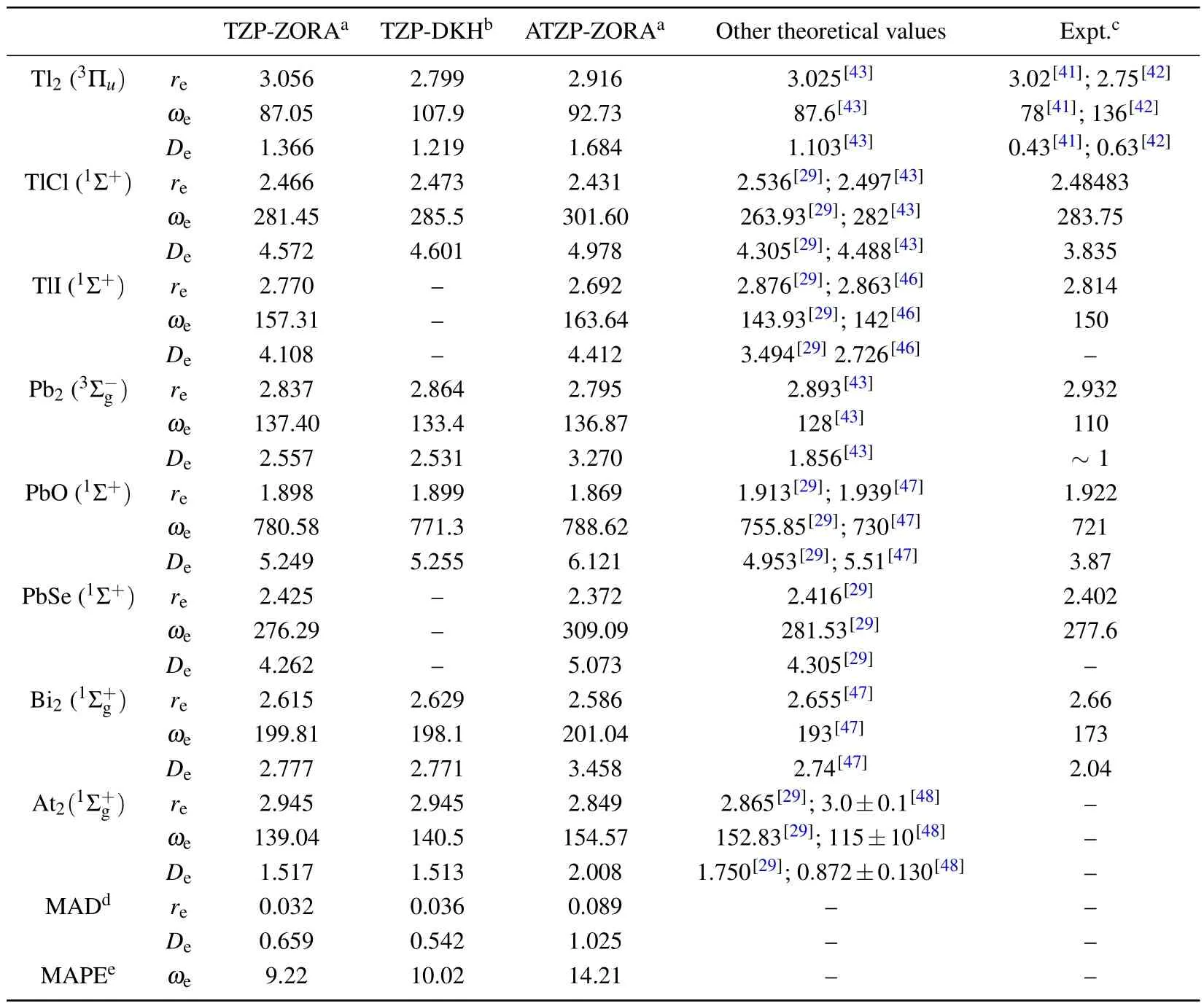
Table 5.(Continued)
3.4.Harmonic vibrational frequency
Alkaline and alkali earth with high atomic numbers may form dimers that have low harmonic vibrational frequencies due to their high molecular weights and large bond lengths.Theoretical and experimental results in Table 5 confirm this expectation.Owing to the two reasons mentioned above, the vibrational frequency of Ba2is the lowest in all frequencies,followed by that of Cs2.It is worth remembering that this behavior is just the opposite of those ones that occur for the bond lengths of these molecules.Owing to bond lengths and molecular weights decreasing,the theoretical and experimental harmonic vibrational frequencies increase significantly from Cs2to CsH and from Ba2to BaH.Also,because of the two factors mentioned in the previous sentence, the ZORA-B3LYP/TZPZORA and ATZP-ZORA harmonic vibrational frequencies increase through the following two processes:Tl2→TlI→TlCl and Pb2→PbSe→PbO.
Except for Ba2, Pt2, and Tl2molecules, the ZORAB3LYP/TZP-ZORA and DKH2-B3LYP/TZP-DKH harmonic vibrational frequencies are very close to each other.For these three molecules, the corresponding theoretical results of 31 cm-1,[24]205 cm-1,[44]and 87.6 cm-1,[43]which are calculated with the DKH-CASSCF/CASPT2/[12s10p8d4f],B3LYP/LANL2DZ,and DKH-CASSCF/CASPT2/ANO-QZP theoretical procedures, respectively, are closer to the ZORAB3LYP/TZP-ZORA values than the DKH2-B3LYP/TZPDKH ones.For Pt2and Tl2, the best agreement with the experimental values of 259 cm-1(Ref.[39]) and 78 cm-1(Ref.[41]) occurs in DKH2-B3LYP/TZP-DKH and ZORAB3LYP/TZP-ZORA, respectively.For, at least, these three dimers, the ZORA-B3LYP/TZP-ZORA harmonic vibrational frequencies show that they are more consistent with the results published in the literature.The ZORA-B3LYP/TZPZORA harmonic vibrational frequencies accord well with ZORA-B3LYP/ANO-RCC-VQZP-unc benchmark theoretical results[29]and with values found in Refs.[24,43–48].In general, the experimental and ZORA-B3LYP/TZP-ZORA values are also in good agreement.Overall, the mean absolute percentage errors (MAPEs) of the ZORA-B3LYP/TZP-ZORA,DKH2-B3LYP/TZP-DKH, and ZORA-B3LYP/ATZP-ZORA results relative to the experimental data are 9.22%, 10.02%,and 14.21%,respectively.
3.5.Dissociation energy
Another characteristic of dimer mainly consisting of alkaline and alkali earth with high atomic numbers is its low dissociation energy.[24]All the theoretical and experimental results in Table 5 for the cesium and barium dimers show this trend.Moreover,just as the harmonic vibrational frequencies appear, Ba2has the lowest value of dissociation energy, followed by Cs2as listed in Table 5.It is worth noticing that all other trends observed for harmonic vibrational frequencies also occur for dissociation energy,namely: (i) the theoretical and experimental dissociation energy values increase from Cs2to CsH and from Ba2to BaH and(ii) the ZORA-B3LYP/TZPZORA and ATZP-ZORA dissociation energy values increase through the series Tl2→TlI→TlCl and Pb2→PbSe→PbO.Certainly,these behaviors of the dissociation energy values of these molecules are related to their bond lengths.
Except for Ba2and Pt2, all other ZORA-B3LYP/TZPZORA and DKH2-B3LYP/TZP-DKH dissociation energy values are very close to each other.For Ba2, the only theoretical result of 0.145 eV found in the literature[24]is closer to the value calculated with the ZORA-B3LYP/TZPZORA model than with the DKH2-B3LYP/TZP-DKH, while for Pt2, the opposite occurs when the experimental dissociation energy of 3.14 eV[39]is considered.In general, the ZORA-B3LYP/ANO-RCC-VQZP-unc and ZORAB3LYP/TZP-ZORA dissociation energy values are also close to each other, while the agreement between our results and those reported in Refs.[24,43–48]is satisfactory.Considering the experimental data,the MADs,computed with the ZORAB3LYP/TZP-ZORA, DKH2-B3LYP/TZP-DKH, and ZORAB3LYP/ATZP-ZORA approach, are equal to 0.659, 0.542,and 1.025 eV, respectively.These deviations can be reduced if spin-orbit coupling, which is generally not negligible for molecules containing elements of the fifth row,is included in the calculations.Another point that draws attention in Table 5 is that all theoretical dissociation energy values for Tl2and Pb2are, at least, twice as high as the experimental values of 0.63 eV[42]and~1 eV,[39]respectively.However,if spin-orbit corrections,estimated in Ref.[43](–0.593 eV and–0.909 eV),are added to ZORA-B3LYP/TZP-ZORA results(1.366 eV and 2.557 eV), the agreement with the experimental data will be improved, since the dissociation energy value of Tl2and Pb2reduce to 0.773 eV and 1.648 eV,respectively.Our main goal in this work is limited to the generation of specific basis sets for the ZORA Hamiltonian,so,the spin–orbit correction goes beyond the scope of this work.
4.Conclusions
In this work, the TZP-ZORA and ATZP-ZORA segmented Gaussian basis sets are extended in order to include the elements of the fifth row.The same precautions taken earlier in generating equivalent sets for elements from H to Xe[30]are maintained here,i.e., we construct the compact and accurate basis sets.The DKH sets, developed by our research group,have been efficiently used to calculate properties involving the electrons not only from the outer shells,but also from the inner shells(see,Ref.[15]).We expect the basis sets presented in this work to have similar performances.Certainly,their best performances occur when they are combined together with the corresponding basis sets developed for the H–Xe elements.[30]
Below,we list some specific conclusions drawn from our results.
(I) It is verified that the MAD of the ionization energies ZORA-B3LYP/TZP-ZORA in relation to the experimental data or in relation to the benchmark theoretical values[29]are slightly lower than the corresponding ones computed with the DKH2-B3LYP/TZP-DKH model.The reliability of the ZORA-B3LYP/TZP-ZORA approach in determining this property is verified through the small values of their MADs.
(II) The experimental and theoretical difficulties in correctly estimating the mean dipole polarizability of any system containing many electrons are well documented in the literature.The combination of the ZORA-B3LYP method with the ZORA-ATZP basis set seems to be a promising procedure for performing this task, since these results generally accord very well with experimental and recommended data[37]and also with benchmark theoretical values.[29]As expected, the performance of the TZP-ZORA set in estimating atomic polarizabilities is very poor,since this set lacks diffuse Gaussian functions to properly describe electrons far away from nuclei.
(III) For the fifteen molecules studied here,it is verified that relative to the experimental data,the deviations and errors obtained from the ZORA-B3LYP/TZP-ZORA and DKH2-B3LYP/TZP-DKH results are low.In addition, bond lengths,harmonic vibrational frequencies,and dissociation energy values calculated with the TZP-ZORA basis set are generally close to previously published theoretical values.
(IV) From our calculations of atomic ionization energy values and bond lengths, harmonic vibrational frequencies,and dissociation energies of a set of diatomic molecules, it is quite clear that the addition of diffuse functions to the TZPZORA set,i.e., the use of the ATZP-ZORA set, can increase computational time, but cannot improve the results presented in this work at all.
The parameters of the TZP-ZORA and ATZP-ZORA basis sets for H–La and Hf–Rn are available from the following website https://qcgv.ufes.br/.
Acknowledgment
Project supported by the Conselho Nacional de Desenvolvimento Cient′?fico Tecnol′ogico(Brazilian Agency).
- Chinese Physics B的其它文章
- Robustness of community networks against cascading failures with heterogeneous redistribution strategies
- Identifying multiple influential spreaders in complex networks based on spectral graph theory
- Self-similarity of complex networks under centrality-based node removal strategy
- Percolation transitions in edge-coupled interdependent networks with directed dependency links
- Important edge identification in complex networks based on local and global features
- Free running period affected by network structures of suprachiasmatic nucleus neurons exposed to constant light

