A Hybrid Self-adaptive Conjugate Gradient Projection Method Without Lipschitz Continuity and Its Applications
YUAN Zihang(袁梓航) ,WANG Yun(王云) ,LIU Pengjie(劉鵬杰),2 ZHUO Yue(卓越) ,ZHOU Jincheng(周金誠)
(1. School of Mathematics, China University of Mining and Technology, Xuzhou 221116, China; 2. Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University, Kowloon 999077, China)
Abstract: The conjugate gradient projection method is an effective algorithm for solving large-scale nonlinear monotone equations with convex constraints.In this paper,based on the four classical conjugate parameters,an effective hybrid self-adaptive conjugate gradient projection method is proposed by using hybridization strategy and projection technique.The search direction satisfies the sufficient descent and trust region properties independent of any line search.The global convergence of the new method is analyzed and proved without the Lipschitz continuity assumption.The results of the numerical experiments show the computational efficiency of the proposed method.Finally,the applicability of the new method is verified by some numerical experiments on sparse signal restoration.
Key words: Nonlinear monotone equations;Conjugate gradient projection method;Convergence property;Compressed sensing
1.Introduction
In this paper,we consider the following constrained nonlinear monotone equations
whereC ?Rnis a closed convex set,andF:RnRnis a continuous and monotone mapping.The monotone property ofFmeans that
Throughout this paper,∥·∥stands for the Euclidean norm.PC[·] is the projection mapping from Rnonto the nonempty closed convex setC,i.e.,PC[x]arg min{∥y ?x ∥|.
Many practical problems in many fields of sciences and engineering can be transformed into the above nonlinear equations (1.1),such as the compressed sensing problem[1]and the chemical equilibrium system[2],and the wide application promotes many scholars to research the efficient methods for solving (1.1).In these ways,the derivative-free projection-based method is efficient for dealing with large-scale smooth or non-smooth constrained nonlinear equations because of their simplicity and low storage requirements,including spectral gradient projection method[3-4],two-term conjugate gradient projection method (CGPM)[5-9],threeterm CGPM[10-11]and so on.
In this part,we devote to developing a hybrid self-adaptive CGPM for solving (1.1).For this purpose,we first briefly review the conjugate gradient method (CGM) for the unconstrained optimization problem min{f(x)|Rn},wheref: RnR is continuously differentiable,and its gradientFk:F(xk)?f(xk) forxkRn.The iterative form of the search direction of the traditional two-term CGM is
whereβkis the conjugate parameter.Denoteyk-1Fk ?Fk-1,andβkin classical CGMs including Hestenes-Stiefel(HS)method[12],Fletcher-Reeves(FR)method[13],Polak-Ribière-Polyak (PRP) method[14-15]and Dai-Yuan (DY) method[16]are listed as follows:
It is widely known that the hybrid self-adaptive CGM has appealing theoretical properties and numerical performance in unconstrained optimization,such as Refs.[17-19].To this end,many scholars have made efforts to extend the hybrid CGM for solving large-scale nonlinear systems of monotone equations.For example,based on the hybrid conjugate parameterin [18],SUN and LIU[7]proposed a modified parameter as follows,
where?>1,and extended it to solve problem (1.1).Motivated by the parameterYIN et al.[8]introduced a generalized hybrid parameter,i.e.,
?Based on four famous conjugate parameters and hybridization strategy,an improved hybrid self-adaptive conjugate parameter is proposed to ensure that the search direction generated by the new method does not depend on any line search to satisfy sufficient descent condition and trust region property.
?The convergence results of the proposed method are given.Compared with the traditional CGPM,the new method does not requireFto satisfy the Lipschitz continuity,which is the theoretical advantage of our method.
?The numerical results show that our method is valuable and promising for solving large-scale constrained nonlinear equations and sparse signal recovery problems.
The remainder of this paper is organized as follows.In Section 2,we propose a hybrid self-adaptive CGPM,and then the corresponding convergence analysis results are given.In Section 3,the numerical experiments and comparison are performed in solving constrained nonlinear equations.Applications of the proposed method in solving sparse signal restoration are introduced in Section 4.The conclusions are given in the final section.
2.Algorithm and Convergence Property
Based on the existing adaptive line search[3],we extend the search directiondkdefined by (1.3)-(1.5) to solve the nonlinear monotone equations (1.1).Now,we describe the steps of our method in detail.
In what follows,we analyze the global convergence of the HACGP,and always assume that the following assumptions hold.
(A1) The solution set of (1.1),denoted by?,is nonempty;
(A2) The mappingFis monotone and continuous on Rn.
Note that the continuity in (A2) is weaker than the Lipschitz continuity,which is a common assumption of methods for solving equations (1.1).
Lemma 2.1For allk ≥0,the search direction sequence{dk},generated by the HACGP,satisfies the sufficient descent property
and the trust region property
and the sufficient descent property (2.4) is proved.
Moreover,due to∥Fk∥∥dk∥cos〈Fk,dk〉the following relation holds,
In addition,from (1.3) and (2.6),we obtain
The proof is completed.
Lemma 2.2Let the sequences{xk}and{zk}be generated by the HACGP.For any,the sequence{∥xk ?∥}is convergent,and sequence{xk}is bounded.Furthermore,it holds that
ProofThe proof is similar to Lemma 4 in [10],so it is omitted here.
Theorem 2.1The sequence{xk},generated by the HACGP,globally converges to a solution of equations (1.1).
ProofThe following two cases are given.
Based on (2.5),it holds that
According to Lemma 2.2,the sequence{xk}is bounded,and noticing from the continuity ofF,we know that there exists a positive constantMsuch that
whereKis an infinite index set.Based on (2.4),we get
Settingin the inequality above,together with the continuity ofFand (2.8),we yield
In addition,from (2.1),we obtain
3.Numerical Experiments
The effectiveness of HACGP is verified by numerical experiments (constrained nonlinear monotone equations) and it is compared with three existing algorithms,Algorithm 3.1 in [7](represented by HCGP),Algorithm 2.1 in[5](represented by PDY),and HCGP-ALS(HCGP with) with adaptive line search (2.1).All codes were written in MATLAB R2014b and ran on a 64-bit Dell laptop with an Intel(R) Xeon(R) E-2186M CPU (2.90) processor,128.00 GB RAM and Windows 10 operating system.
The parameters in HACGP are selected as follows:ρ0.5,ζ1,δ0.01,λ0.001,ν0.8,μ1.4 andγ1.6,and those in HCGP and PDY are both the same as the original literature.For HCGP-ALS,the parameters are selected as follows:ρ0.5,ζ1,δ0.01,λ0.001,ν0.8,?1.4 andγ1.6.
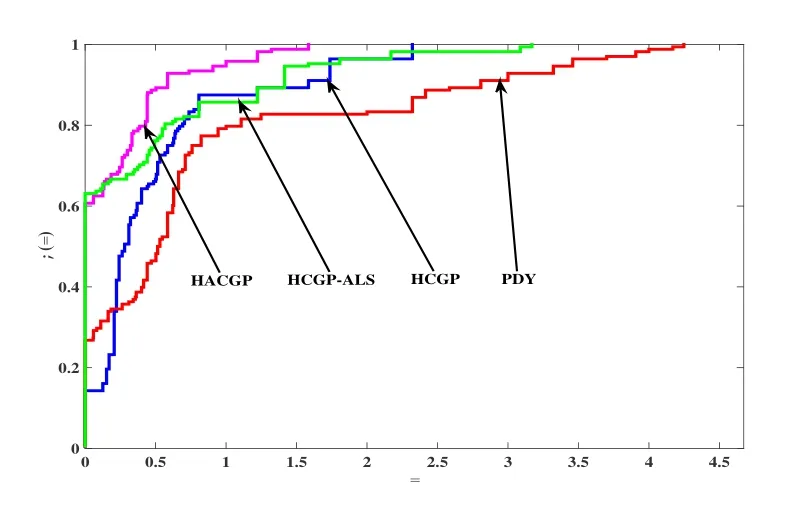
Fig.3 Performance profiles on Itr
The numerical results show that the algorithm in this paper performs well in most cases and can successfully solve all the tested problems.Moreover,the performance chart proposed by Dolan and Moré[20]makes the test results clearer and enables to illustrate and compare Tcpu,NF and Itr related performance profiles separately in an intuitive way.For more information about performance profiles,see [20].According to the interpretation of the performance profiles,the higher a curve is located,the more efficient the corresponding algorithm is.Therefore,from the visual comparison in Figs.1-3,we know that the HACGP is a winner,and it outperforms the other three algorithms in Tcpu,NF and Itr.Furthermore,the comparison of HACGP and HCGP-ALS shows that the proposed parameteris valid and meaningful.
4.Applications in Sparse Signal Restoration
In this section,the HACGP is applied to solve the sparse signal recovery problem,and we compare it with HCGP[7].
First,we know that the compressed perceptual model is used to recover the sparse signal of an underdetermined linear systemAxb,whereRm×n(m ?n) is a linear mapping andRmis the observed data.In fact,the sparse signal recovery problem is solved by solving the following?1-norm regularization optimization problem
whereκ>0 is a constant that balances data fitting and sparsity,and∥·∥1and∥·∥2denote the?1-norm and?2-norm,respectively.
The objective function of problem (4.1) is reformulated from a non-smooth convex case to a convex quadratic programming via [21].By introducing auxiliary variablesRnandRn,the arbitrary vectorRncan be decomposed into the following two parts
whereu ≥0,v ≥0.Further,we obtain the following standard form
Clearly,(4.2) is a convex quadratic programming problem due to the fact thatHis a semi-positive definite matrix.Then,according to the first-order optimality condition of(4.2),zis the minimum point of (4.2) and is a solution of the following optimization problem,
where the functionFis a vector value and “min” is interpreted as the minimum of the components.It follows from Lemma 3 in [22] and Lemma 2.2 in [23] thatF: R2nR2nis(Lipschitz) continuously monotone.Therefore,we can apply the proposed method to get the solution of the above optimization problem.
In these experiments,the main objective is to recover a one-dimensional sparse signal of lengthnfrommobservations,andm ?n.The parameters of HACGP are the same as those selected in Section 3;the parameters of HCGP are taken from Section 4 in [10].All codes were written using MATLAB R2014b and ran on a 64-bit Dell laptop with an Intel(R)Xeon(R) E-2186M CPU (2.90 GHz) processor,128.00 GB of RAM,Windows 10 operating system.Typically,the quality of the recovery is measured by the mean squared error (MSE),i.e.,
In our experiments,the number of non-zero componentsxis denoted byr.For a given triplet (m,n,r),we generate the test data using the following MATLAB code.
xzeros(n,1);% initialize the original sparse signal
qrandperm(n);
x(q(1:r))randn(r,1);
Arandn(m,n);
Aorth(A’)’;% orthonormalize the rows ofA
bA ?x+0.001?randn(m,1);
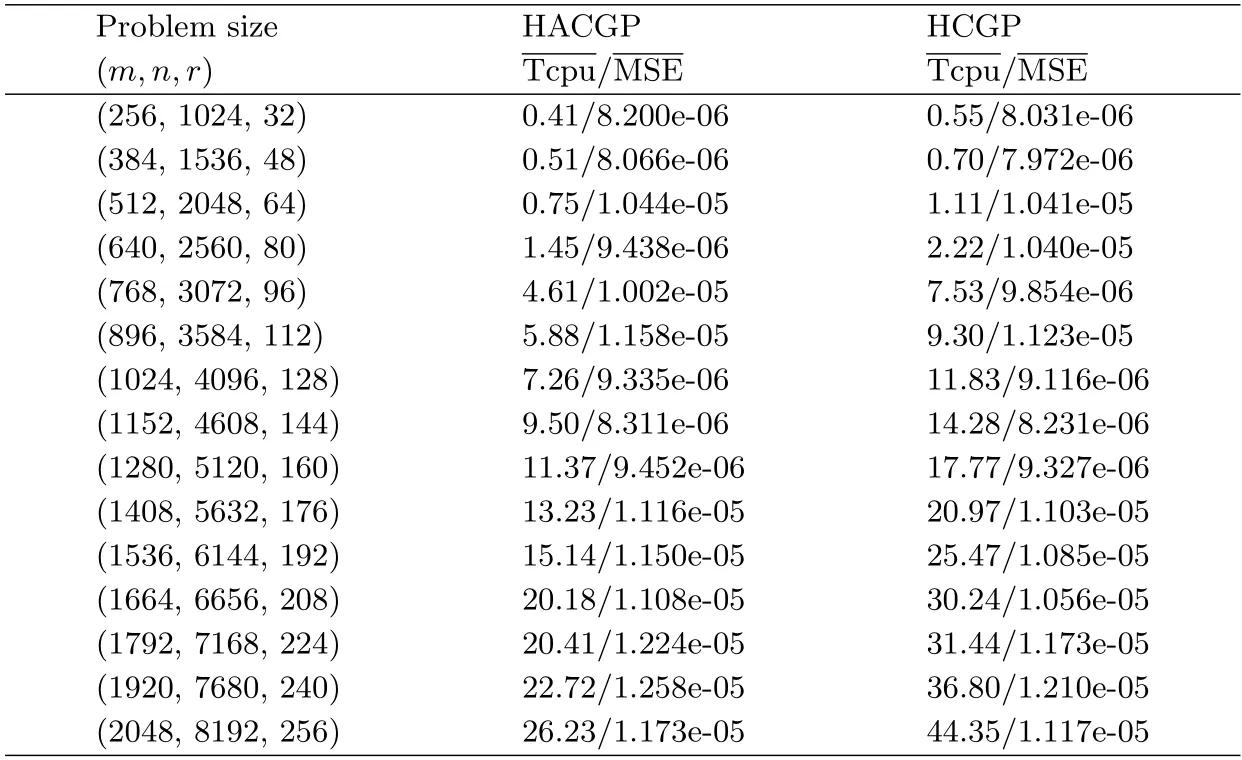
Tab.1 Numerical results for sparse signal restoration
5.Conclusions
In this work,based on the four classical conjugate parameters,we propose a hybrid self-adaptive CGPM for solving the constrained nonlinear monotone equations.The search direction satisfies the sufficient descent and trust region properties,automatically.Under some general assumptions,we analyze and obtain global convergence of the proposed method without the Lipschitz continuity.The method is then compared with other existing methods and the numerical results indicate that the proposed method is efficient.Furthermore,the new method is used to recover a sparse signal from a contaminated sampling measurement and the results are practical and promising.
- 應用數學的其它文章
- 約束優(yōu)化問題的單參數填充函數算法
- Iterative Regularization Method for the Cauchy Problem of Time-Fractional Diffusion Equation
- K-power雙線性系統(tǒng)基于Laguerre函數的保結構模型降階方法
- Lur’e主從系統(tǒng)的二次反饋型脈沖同步控制
- 帶有隔離的COVID-19隨機SQIR模型研究
- A New Inertial Tseng’s Extragradient Method for Solving Split Variational Inclusion Problems and Fixed Point Problems

