洪麗君,劉金靈,洪曉春

(1.中山大學(xué)數(shù)學(xué)學(xué)院,廣東 廣州 510275;2.中南財(cái)經(jīng)政法大學(xué)統(tǒng)計(jì)與數(shù)學(xué)學(xué)院,湖北武漢 430073;3.云南財(cái)經(jīng)大學(xué)統(tǒng)計(jì)與數(shù)學(xué)學(xué)院,云南 昆明 650221)

1 引言和主要結(jié)果

考慮擾動(dòng)虧格1形式的二次可逆系統(tǒng)

其中ε(0<ε?1)是一個(gè)實(shí)數(shù),,p(x,y),q(x,y)都是關(guān)于x,y的多項(xiàng)式,并且

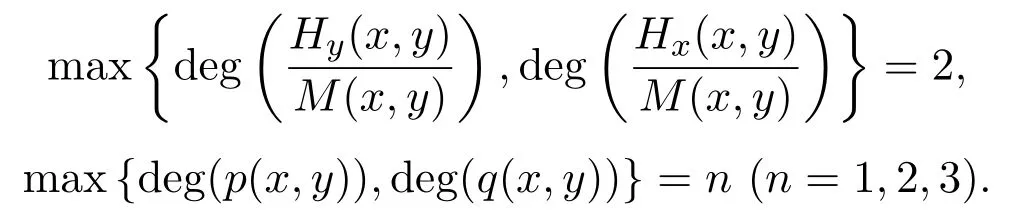
當(dāng)ε=0時(shí),系統(tǒng)(1.1)是一個(gè)二次可逆系統(tǒng),而且是一個(gè)可積系統(tǒng),它有一個(gè)中心.函數(shù)H(x,y)是其帶有積分因子M(x,y)的一個(gè)首次積分,也就是說(shuō),可以定義一個(gè)連續(xù)的周期環(huán)域

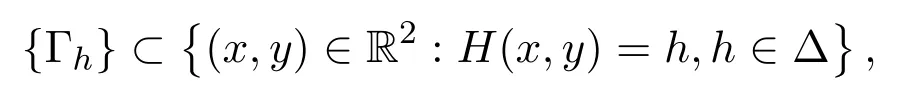
它們是定義在最大開區(qū)間?=(h1,h2)上的.本文要解決的問(wèn)題是:對(duì)于任意小數(shù)ε,系統(tǒng)(1.1)可以從周期環(huán)域{Γh}中分支出多少個(gè)極限環(huán)？人們知道,在周期軌道的任何緊致區(qū)域中,系統(tǒng)(1.1)的極限環(huán)個(gè)數(shù)不超過(guò)以下阿貝爾積分I(h)的孤立零點(diǎn)個(gè)數(shù) (見文獻(xiàn) [1-6]).

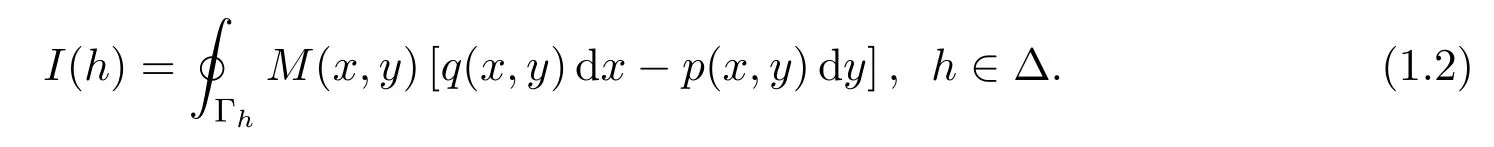
對(duì)于虧格 1形式的二次可逆系統(tǒng),文獻(xiàn) [7]顯示其可分為 22種基本類型,具體分為(r1)-(r22).當(dāng)n較小時(shí),對(duì)于零點(diǎn)個(gè)數(shù)的上界問(wèn)題,文獻(xiàn)[8]研究了系統(tǒng)(r1),系統(tǒng)(r2)是一個(gè)哈密頓系統(tǒng);文獻(xiàn)[9]研究了系統(tǒng)(r3)-(r6);文獻(xiàn)[10-14]研究了系統(tǒng)(r9)-(r13)及(r16)-(r22).

本文再次研究系統(tǒng)(r19)和(r20),獲得了一些新的結(jié)果(見表1).

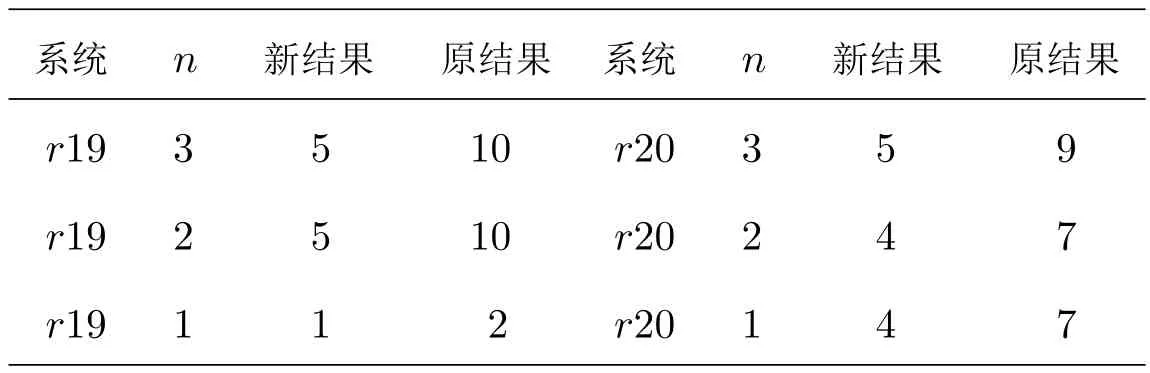
表1 新結(jié)果與原結(jié)果的對(duì)比

系統(tǒng)(r19)和(r20)的形式如下:

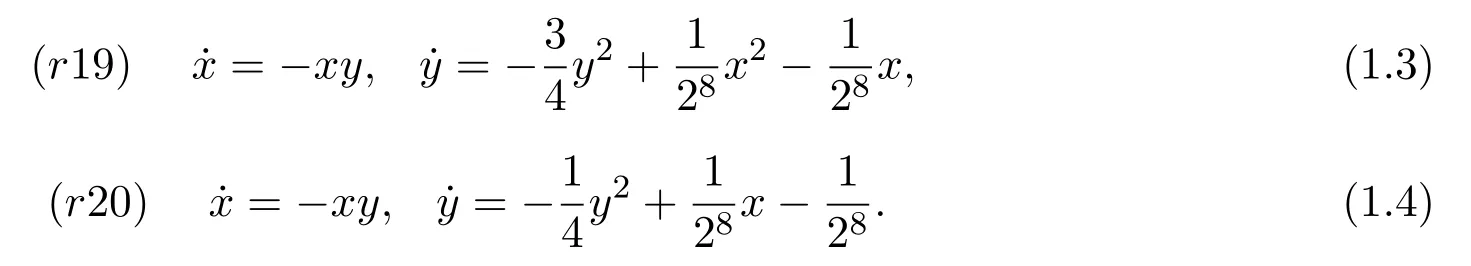
由(1.3)式-(1.4)式,可得它們的首次積分為

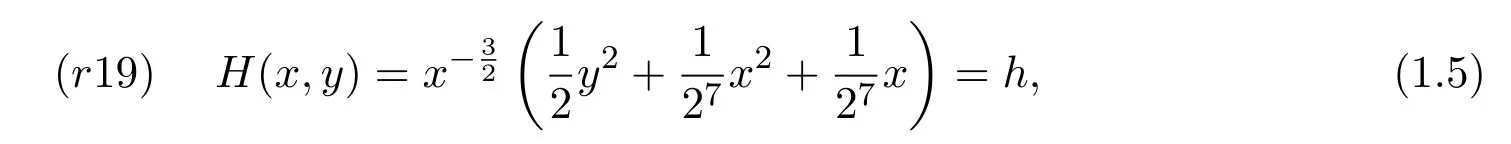
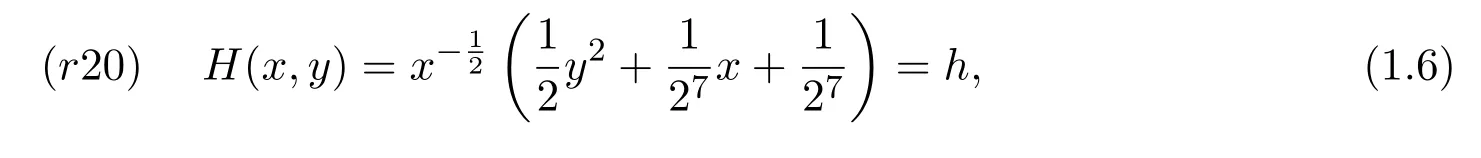
(r19)是一個(gè)可積非哈密頓二次系統(tǒng),其幾乎所有的軌道都是四次曲線,它有一個(gè)中心(1,0),一條積分曲線x=0,一族周期軌道(見圖1).

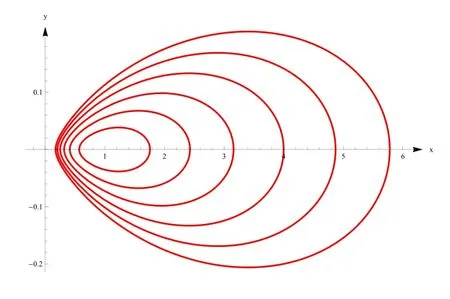
圖1 系統(tǒng)(r19)的周期軌道

(r20)也是一個(gè)可積非哈密頓二次系統(tǒng),其幾乎所有的軌道都是二次曲線,它有一個(gè)中心(1,0),一條積分曲線x=0,一族周期軌道(見圖2).

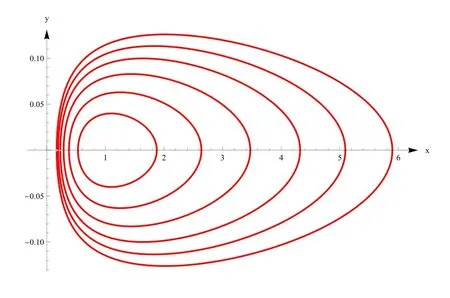
圖2 系統(tǒng)(r20)的周期軌道

對(duì)于系統(tǒng)(r19),文獻(xiàn)[10]給出了包含下面定理的結(jié)論.

定理 1.1[10]對(duì)于任意的n次多項(xiàng)式p(x,y)和q(x,y),阿貝爾積分I(h)的孤立零點(diǎn)個(gè)數(shù)的上界線性依賴于n.具體情況是:當(dāng)n≥4時(shí),上界為6n?12;當(dāng)n=3,2時(shí),上界為 10;當(dāng)n=1時(shí),上界為2;當(dāng)n=0時(shí),上界為0.

對(duì)于系統(tǒng)(r20),文獻(xiàn)[11]給出了包含下面定理的結(jié)論.

定理 1.2[11]對(duì)于任意的n次多項(xiàng)式p(x,y)和q(x,y),阿貝爾積分I(h)的孤立零點(diǎn)個(gè)數(shù)的上界線性依賴于n.具體情況是:當(dāng)n≥3時(shí),上界為6n?9;當(dāng)n=1,2時(shí),上界為 7;當(dāng)n=0時(shí),上界為0.

本文的主要結(jié)果包含下面的定理.

定理 1.3對(duì)于n次任意的多項(xiàng)式p(x,y)和q(x,y)(n=1,2,3),阿貝爾積分I(h)的孤立零點(diǎn)個(gè)數(shù)的上界如下:對(duì)于系統(tǒng)(r19),當(dāng)n=3,2時(shí),上界為5;當(dāng)n=1時(shí),上界為1.對(duì)于系統(tǒng)(r20),當(dāng)n=3時(shí),上界為5;當(dāng)n=2,1時(shí),上界為4.

新結(jié)果與原結(jié)果的對(duì)比情況見表1.

本文后面部分的結(jié)構(gòu)如下:第二部分,努力尋找阿貝爾積分I(h)的簡(jiǎn)單表示方法,獲得了它的一種簡(jiǎn)單表示.第三部分,對(duì)于系統(tǒng)(r19),研究其阿貝爾積分I(h)與J1(h)之間的關(guān)系;對(duì)于系統(tǒng)(r20),研究其阿貝爾積分I(h)與之間的關(guān)系.獲得了兩個(gè)Riccati方程.第四部分,使用Riccati方程方法證明了定理1.3.第五部分,給出一個(gè)簡(jiǎn)短的結(jié)論.

2 阿貝爾積分 I(h)的簡(jiǎn)單表示

3 Riccati方程

4 阿貝爾積分I(h)零點(diǎn)個(gè)數(shù)的上界

文獻(xiàn)[10-11]僅考慮了函數(shù)α(h),β(h),B(h)和D(h)關(guān)于h的次數(shù).現(xiàn)在,研究這些函數(shù)關(guān)于h的次數(shù),還考慮其奇偶性,而且考慮h的取值范圍,從而得到更好的結(jié)果.在本節(jié)中,使用Riccati方程方法證明定理1.3.

對(duì)于后面的內(nèi)容,用?I(h)表示阿貝爾積分I(h)在區(qū)間?中的零點(diǎn)個(gè)數(shù),需要用到下面的引理.

5 結(jié)論

在本文中,對(duì)于次數(shù)為n(1≤n≤3)的任意多項(xiàng)式擾動(dòng)下的虧格1形式二次可逆系統(tǒng)(r19)和(r20),使用Riccati方程方法,研究其阿貝爾積分孤立零點(diǎn)個(gè)數(shù)的上界,得到如下結(jié)果:對(duì)于系統(tǒng) (r19),當(dāng)n=3,2時(shí),上界為5,當(dāng)n=1時(shí),上界為1;對(duì)于系統(tǒng)(r20),當(dāng)n=3時(shí),上界為5,當(dāng)n=2,1時(shí),上界為4.這些結(jié)果均優(yōu)于原結(jié)果.