方珍潔,龍憲軍

(重慶工商大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院 重慶 400067)

1 引言

2 相關(guān)定義與引理

3 算法與收斂性證明

4 數(shù)值實驗

為了體現(xiàn)本文討論的算法的數(shù)值效果,本節(jié)通過例子將算法3.1與文獻[16]中的算法4(記為RITEM算法),文獻[14]中的算法3.5(記為ITEM算法)和文獻[15]中的算法1(記為MTEM算法)進行比較.所有代碼均在MATLAB R2019b和Windows10系統(tǒng)下運行,計算機基本參數(shù)為Intel(R)Core(TM)i5-10210U CPU@1.60GHz 2.11GHz和16GB內(nèi)存.

例 4.1設(shè)算子F:Rm→Rm(m=50,100)滿足F(x)=Mx+q,其中q∈Rm,同時M=NNT+S+D,其中N∈Rm×m,S∈Rm×m斜對稱矩陣,D∈Rm×m對角元素非負的對角矩,可行集C=R+m.各參數(shù)選取如下:

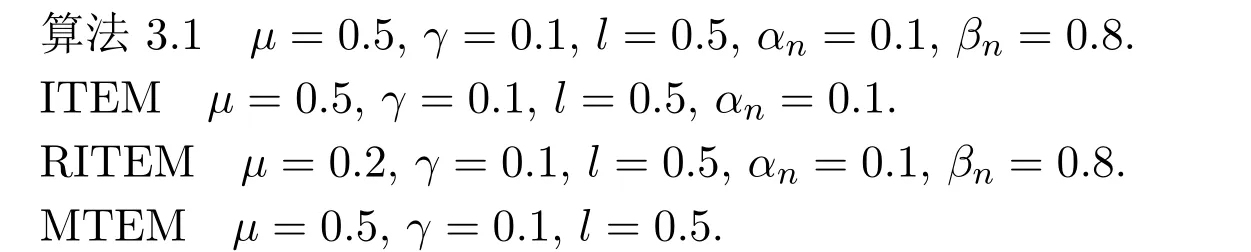
初始點x0=(1,1,···,1)T∈Rm,終止條件為Dn=∥xn+1?xn∥,測試結(jié)果見圖1,圖2和表1.通過圖1,圖2和表1可以發(fā)現(xiàn),算法3.1比文獻[16]中RITEM算法,文獻[14]中ITEM算法和文獻[15]中MTEM算法收斂效果更好.

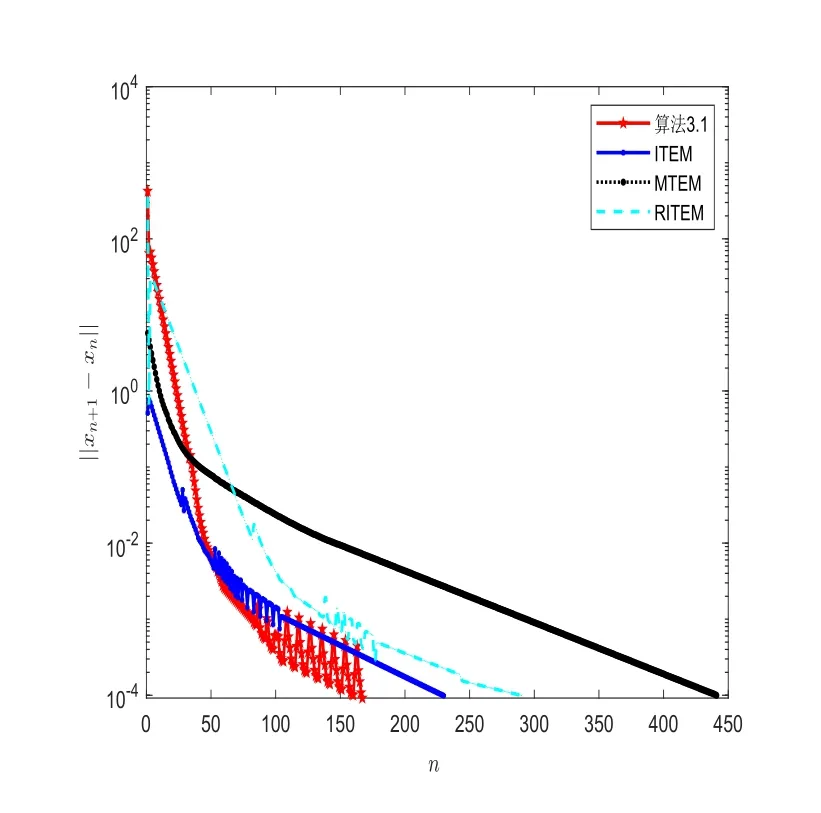
圖1 固定誤差比較圖

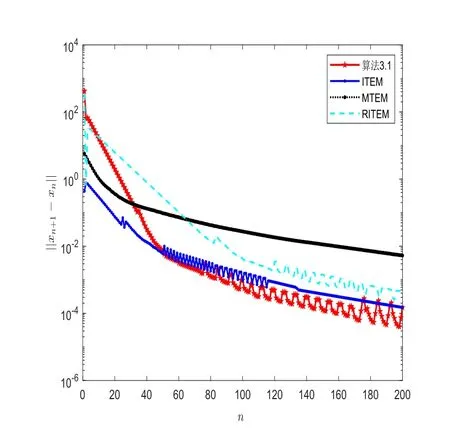
圖2 固定迭代步數(shù)比較圖

表1 例4.1算法結(jié)果對比表

例4.2假設(shè)H=l2,令

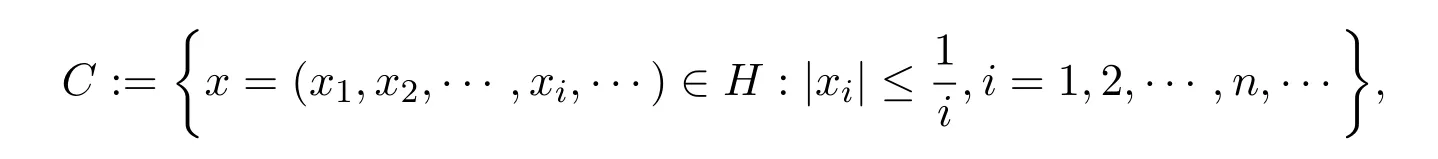
定義算子F:C→H,存在α>0,滿足

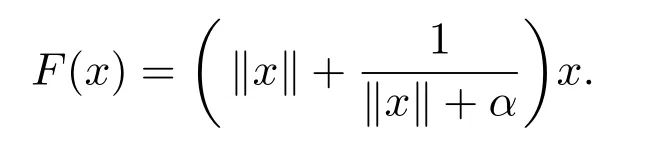
顯然,F在H上是偽單調(diào)的且一致連續(xù)的,在C上是序列弱連續(xù)的.令α=0.5,可行集

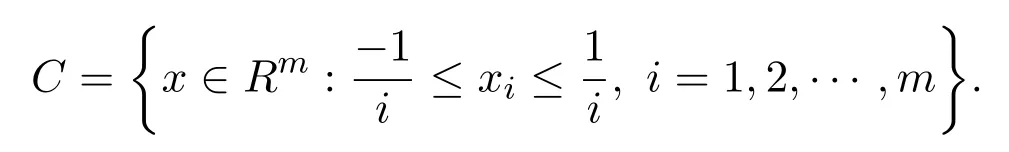
各參數(shù)選取如下:

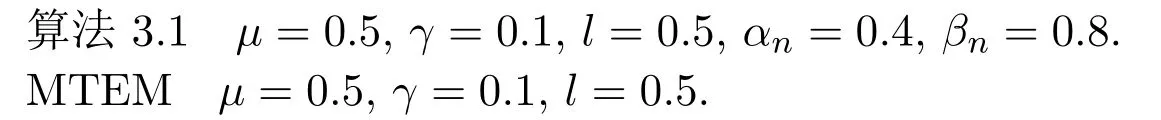
初始點x0=[0,1]m,用∥xn∥來估算第n步迭代誤差值.由于F既不是單調(diào)的,也不是Lipschitz連續(xù)的,故文獻[16]中RITEM算法和文獻[14]中ITEM算法不適用于本例.測試結(jié)果見圖3,圖4和表2.通過圖3,圖4和表2可以發(fā)現(xiàn),算法3.1比文獻[15]中MTEM算法迭代次數(shù)少,收斂速度更快.

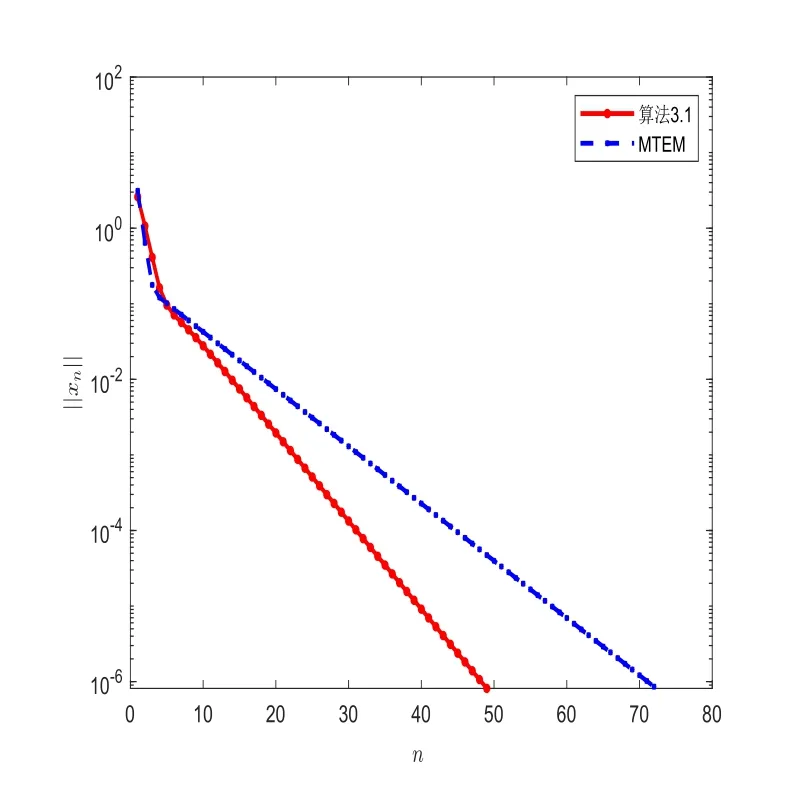
圖3 固定誤差比較圖

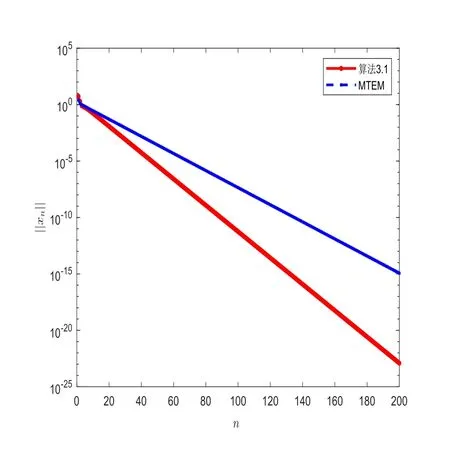
圖4 固定迭代步數(shù)比較圖

表2 例4.2算法結(jié)果對比表

從數(shù)值實驗的結(jié)果來看,得出結(jié)論:

(i)由圖 2可得,在相同的迭代步數(shù)下,算法 3.1比 RITEM 算法,MTEM 算法和ITEM算法的誤差Dn更小,更接近于變分不等式的解.

(ii)由圖 1和表 1可得,在達到相同的誤差Dn時,算法 3.1比 RITEM 算法,MTEM算法和ITEM算法運行的時間更短,迭代步數(shù)更少.

(iii)由例4.2可得,算法3.1和MTEM算法比ITEM算法和RITEM算法適用范圍更廣.

(iv)由圖4可得,在相同的迭代步數(shù)下,算法3.1比MTEM算法得到的誤差更小.

(v)由圖3和表2可得,在達到相同誤差時,算法3.1比MTEM算法迭代步數(shù)更少,運行時間更短.

(vi)算法3.1,RITEM算法,ITEM算法和MTEM算法均收斂于變分不等式的解,算法3.1優(yōu)于RITEM算法,ITEM算法和MTEM算法.