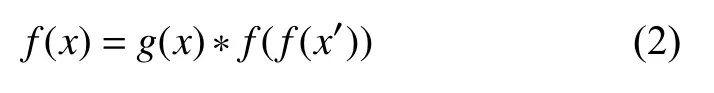任 憑,張 杰,關(guān) 永

1(北京化工大學 信息科學與技術(shù)學院,北京 100029)

2(首都師范大學 信息工程學院,北京 100048)

形式化方法是通過數(shù)學建模和數(shù)學歸納等方法去驗證目標的性質(zhì)規(guī)范以及確保目標的正確性和可靠性的一條重要途徑,其廣泛應(yīng)用于計算機軟硬件的規(guī)范,開發(fā)和驗證.

形式化驗證一般分為等價性檢驗,模型檢驗和定理證明3 種,并且驗證方式各不相同.等價性檢驗的方法主要是通過檢驗?zāi)繕诵薷那昂蟮囊恢滦?來確保修改后的目標至少包含修改前的性質(zhì),但是不能進行特定性質(zhì)或規(guī)范的驗證.模型檢驗的特點是完全自動化,但是存在狀態(tài)空間爆炸的問題,不能用于驗證無限狀態(tài)空間的目標.定理證明的形式化方法是將待驗證的目標和規(guī)范通過數(shù)學建模,描述為一系列的邏輯語言,并通過邏輯演算的方式,證明目標是否具有規(guī)范所描述的性質(zhì).定理證明的驗證方法可以對目標的所有狀態(tài)空間進行建模和驗證,與傳統(tǒng)的仿真測試相比,測試空間更加完備,其驗證結(jié)果具有相當高的可靠性.

當前用于定理證明方法的主流工具有半自動的一階定理證明器Proverif,高階定理證明器HOL4,Isabelle等;也有全自動定理證明器SmartVerif.它們各有優(yōu)劣,半自動工具功能強大,拓展性高,但是學習門檻高;全自動工具入門容易但功能略遜一籌,實用性不如半自動定理證明器.本文用的是基于Standard ML 函數(shù)式語言的半自動高階定理證明器HOL4.

近年來,隨著形式化方法和定理證明器系統(tǒng)被廣泛應(yīng)用于數(shù)學定理[1],計算機軟件[2],硬件[3],方法[4,5]以及協(xié)議[6]的驗證和證明,系統(tǒng)自帶的數(shù)據(jù)結(jié)構(gòu)和定理庫已不能滿足所有形式化工作的需要;因此,用戶在進行形式化建模時,常常需要自定義數(shù)據(jù)結(jié)構(gòu),特別是在HOL4中定義遞歸函數(shù)時用戶必須考慮函數(shù)的終止問題[7],這就給遞歸函數(shù)的形式化建模帶來困難.

1 問題的提出

介紹終止證明問題之前首先需要了解什么是遞歸函數(shù).對于任意函數(shù),定義函數(shù)的語句描述了輸入與輸出之間的邏輯關(guān)系,當輸入任意符合要求的x,都可以得到其對應(yīng)的唯一輸出.一般非遞歸函數(shù)f(x)在定義時可以調(diào)用外部函數(shù),但不會調(diào)用函數(shù)自身,如圖1所示.

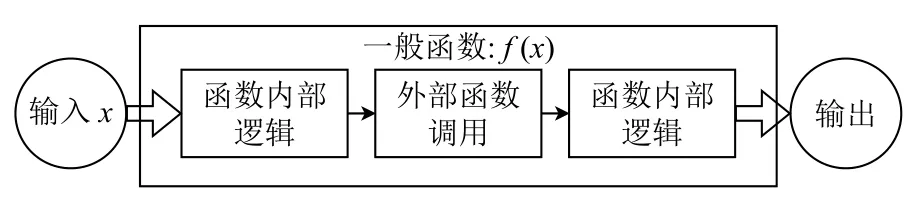
圖1 一般非遞歸函數(shù)f(x)

而與之不同的是,遞歸是通過調(diào)用自身的代碼來解決問題,遞歸方法是計算機科學的核心思想之一[8].在使用遞歸函數(shù)進行建模的過程中,如果考慮不周,使得在某些輸入的情況下,出現(xiàn)無限遞歸的情況,如圖2所示.在形式化建模中不允許遞歸函數(shù)無限調(diào)用自身無法得到輸出的情況存在.因此,建立滿足終止證明規(guī)范的遞歸函數(shù)模型是完成遞歸函數(shù)形式化證明的必要條件.

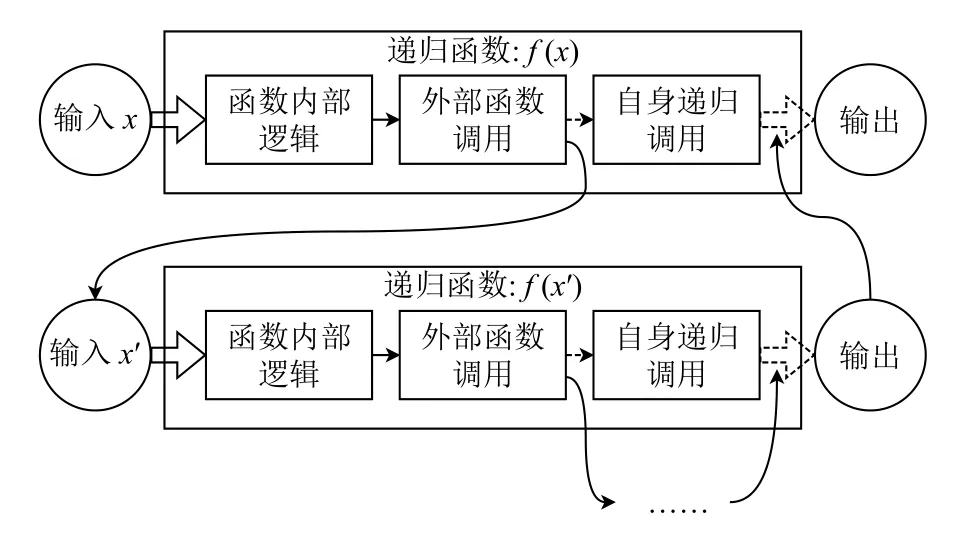
圖2 缺少終止條件的遞歸函數(shù)f(x)

為了使遞歸函數(shù)的形式化模型能夠滿足規(guī)范,需要在遞歸調(diào)用之前添加一個判斷語句,如圖3所示,使得輸入?yún)?shù)在滿足某些特定條件下不再進行遞歸,而是得到相應(yīng)的輸出;而結(jié)束遞歸的判斷條件被稱為遞歸出口或終止條件.

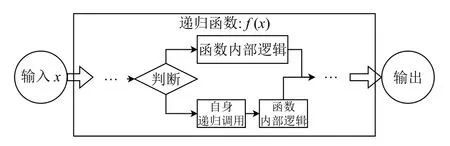
圖3 有終止條件的遞歸函數(shù)

并且,在形式化建模過程中定義遞歸函數(shù),與使用非形式化語言定義函數(shù)的過程有很大的區(qū)別:在非形式化的定義當中,一個沒有終止條件或終止條件不完備的遞歸函數(shù)也能被成功定義,直到它在實際調(diào)用中發(fā)生錯誤時才會拋出錯誤;而由于形式化方法的嚴謹性,在其定義遞歸函數(shù)時,首先必須證明它滿足“輸入集中的任意元素在輸出集中都存在唯一對應(yīng)”的規(guī)范,該證明過程被稱為終止性證明,若無法完成終止證明,就無法成功定義且使用該函數(shù).所以,在HOL4中定義遞歸函數(shù)的關(guān)鍵是要確定其終止條件.在終止條件不夠全面的情況下,終止證明必然失敗,同時證明過程將暴露終止條件中的問題,幫助用戶發(fā)現(xiàn)和補全終止條件的漏洞.然而,即使保證了終止條件的完備性,為什么定理證明器仍然無法自動完成所有遞歸函數(shù)的終止證明?

在一些定理證明器的定理庫中,存在列表等基礎(chǔ)的數(shù)據(jù)結(jié)構(gòu)和相關(guān)的性質(zhì)定理,當使用這些結(jié)構(gòu)進行遞歸定義時,定理證明器基本能夠自動的完成終止證明.而在HOL4 定理證明器中,存在集合結(jié)構(gòu)和相關(guān)的定理庫,但仍然無法完成一部分集合遞歸函數(shù)的終止證明,這是因為HOL4的集合定理庫中缺少一些集合遞歸函數(shù)終止證明所需的定理,這些所需定理可以用已存在的定理推導得到,但是半自動定理證明器在自動進行終止證明的過程中,不能將定理庫中定理進行組合,推導得到新的定理后用于終止證明.所以當系統(tǒng)無法自動完成終止證明時,意味著系統(tǒng)的定理庫中缺少關(guān)鍵的定理或引理,需要用戶自行推導,并將其用于證明終止目標.

當定理證明器無法自動完成終止證明時,如何手動輔助定理證明器完成終止證明是建模過程中的一個難題.本文主要介紹一種解決方案,能夠用于形式化建模過程中定義遞歸函數(shù)所產(chǎn)生的終止證明問題.

2 解決方案

終止證明問題的本質(zhì)是通過定理證明的形式化方法證明新定義的遞歸函數(shù)滿足“輸入集中的任意元素在輸出集中都存在唯一對應(yīng)”的規(guī)范.換而言之,遞歸函數(shù)在任意輸入?yún)?shù)時,經(jīng)過有限次遞歸后,終將滿足終止條件,得到相應(yīng)的輸出,所以該問題著重關(guān)注于輸入?yún)?shù)在遞歸過程是否具有不斷接近終止條件的趨勢.

在基于HOL4的形式化建模工作的實踐過程中,本文總結(jié)出定義兩大類定理證明器經(jīng)常無法自動完成終止證明的遞歸函數(shù):

1)使用自定義數(shù)據(jù)結(jié)構(gòu)作為參數(shù)時.在工作過程中驗證新目標時,往往需要用到新的數(shù)據(jù)結(jié)構(gòu),如鏈結(jié)構(gòu),圖結(jié)構(gòu)等等.但是在系統(tǒng)的定理庫中,只有少量自定義數(shù)據(jù)結(jié)構(gòu)的衍生謂詞,性質(zhì)定理和函數(shù),故使用自定義的數(shù)據(jù)結(jié)構(gòu)定義遞歸函數(shù)時,針對不同的遞歸函數(shù),需要構(gòu)建和證明不同的功能函數(shù)和性質(zhì)定理,輔助系統(tǒng)完成終止證明.

2)使用自定義的函數(shù)作為參數(shù)時.

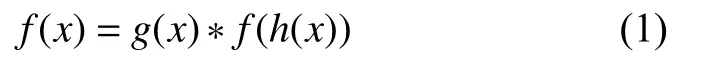
當進行形如式(1)的遞歸函數(shù)定義時(其中h(x)也是自定義的函數(shù)).無論參數(shù)x的數(shù)據(jù)結(jié)構(gòu)是否是自定義結(jié)構(gòu),都需要手動輔助其完成終止證明.

如上所述,具有明確的終止條件是解決終止證明問題的前提,確定待定義的遞歸函數(shù)的終止條件是解決問題的第一步.充分考慮輸入?yún)?shù)的可能性后,一個完整的終止條件通常由復(fù)數(shù)通過析取連接的子條件組成.這些子條件在輸入集合的基礎(chǔ)上分割出若干個非空真子集,若輸入?yún)?shù)屬于這些子條件描述的真子集中,則將得到確定的輸出,否則繼續(xù)遞歸.將終止條件描述的集合稱為輸入集合的終止子集,將終止子集的補集稱為輸入集合的遞歸子集.

假設(shè)目標遞歸函數(shù)設(shè)置了合適的終止條件,即可通過系統(tǒng)中存在的函數(shù)或定義方法,編譯定義語句.在不同的定理證明器中所使用的函數(shù)和方法存在區(qū)別,但是目標和思路大體相同,以下將以HOL4 定理證明器中的函數(shù)和方法為例進行詳細分解.

在HOL4 定理證明器中,使用Hol_defn 方法編譯遞歸函數(shù)的定義語句,系統(tǒng)將剝離出終止條件和遞歸參數(shù),再使用Defn.tgoal 方法即可得到終止證明目標.終止證明目標將剔除與遞歸無關(guān)的定義語句,關(guān)注于輸入?yún)?shù)在遞歸過程中的變化趨勢.

系統(tǒng)通過證明輸入?yún)?shù)在遞歸過程中存在某種指標一步步的由遞歸子集趨近于終止子集來說明函數(shù)必定終止,用戶需要輔助系統(tǒng)的工作首先是明確該指標.例如在遞歸函數(shù)實現(xiàn)的列表遍歷方法中,若終止條件為輸入?yún)?shù)等于空列表,輸入列表的長度在每次遞歸時遞減.因此列表的長度屬性是指標,通過函數(shù)量化列表的長度,并且將終止條件描述的空列表的長度設(shè)定為固定值x,在遞歸的過程中列表長度量化值不斷的向x趨近,即可證明在有限次遞歸后,輸入?yún)?shù)的列表長度必將等于x,從而觸發(fā)終止條件,得到確定的輸出.

在HOL4 定理證明器的終止證明中,需要將以上的趨近關(guān)系改寫成值域為自然數(shù)的單調(diào)遞減函數(shù),終止證明的目標變化為證明該函數(shù)的單調(diào)遞減性.在一些復(fù)雜的遞歸函數(shù)中,如圖的深度優(yōu)先和廣度優(yōu)先遍歷算法中,同時對圖的深度和廣度進行遞歸,需要選取復(fù)數(shù)個指標進行量化,并且構(gòu)建合適的單調(diào)遞減函數(shù).

將終止證明目標轉(zhuǎn)化為單調(diào)遞減性證明后,根據(jù)具體目標不同,證明方法也不同.對于定理證明器無法自動證明的子目標,有可能是缺少一些引理,或者是缺少相關(guān)自定義結(jié)構(gòu)的性質(zhì)定理.應(yīng)推理出詳細的證明過程,證明輔助定理并推進證明目標.

最后將終止證明過程中使用的方法和對策整理為策略,使用定理證明器中的相關(guān)方法將定義語句與策略進行整合,規(guī)范建模格式.

通過詳細分析,無論是使用自定義數(shù)據(jù)結(jié)構(gòu)或定義嵌套遞歸函數(shù)的情況,都可以按照以下方法來進行函數(shù)定義和終止證明.

算法1.終止證明方法(1)分析待定義函數(shù)的輸入集,明確終止條件.(2)分析遞歸過程,確定輸入?yún)?shù)中在遞歸過程中變化最明顯的可量化屬性,定義量化函數(shù),并根據(jù)每個終止子條件設(shè)置固定的量化值.(3)使用定理證明器中手動進行終止證明的定義方法,得到終止證明目標.(4)根據(jù)終止子條件的固定值和輸入?yún)?shù)在遞歸過程中的變化趨勢,構(gòu)建單調(diào)遞減函數(shù),并將終止證明目標簡化為所構(gòu)建函數(shù)的單調(diào)遞減性證明.(5)在證明過程中補充系統(tǒng)定理庫缺少的定理和引理,輔助系統(tǒng)推進證明.如果在證明過程中遇到無法被證明的子目標,回到第(1)步檢查是否缺失終止子條件.(6)完成終止證明,整理定義和證明過程,規(guī)范建模格式.

3 應(yīng)用實例

在實際應(yīng)用中,經(jīng)常會需要用到圖結(jié)構(gòu)來表示節(jié)點與節(jié)點間的連接關(guān)系.而HOL4 定理庫中暫時沒有圖的數(shù)據(jù)結(jié)構(gòu)和相關(guān)性質(zhì)定理,所以需要用戶自定義圖結(jié)構(gòu).因此,下面將以自定義圖結(jié)構(gòu)作為遞歸參數(shù),在HOL4中使用該終止證明方法完成一個遞歸函數(shù)定義和終止證明.在該應(yīng)用中,定義graph 結(jié)構(gòu)包含了存儲圖中節(jié)點信息的集合nodes,以及節(jié)點之間連接關(guān)系的集合edges,其中點集nodes 與邊集edges的論域都為全集,graph的論域為點集nodes 與邊集edges的笛卡爾乘積.

有向圖的定義約束了點集與邊集之間的關(guān)系,故有向圖集是graph的真子集.因此將有向圖定義進行形式化,得到謂詞Digraph 將輸入集切分為有向圖集與非有向圖,并以此作為以graph 作為輸入?yún)?shù)的有向圖的遞歸函數(shù)的第一個終止子條件:當輸入?yún)?shù)不屬于有向圖集時將終止遞歸,如圖4所示.

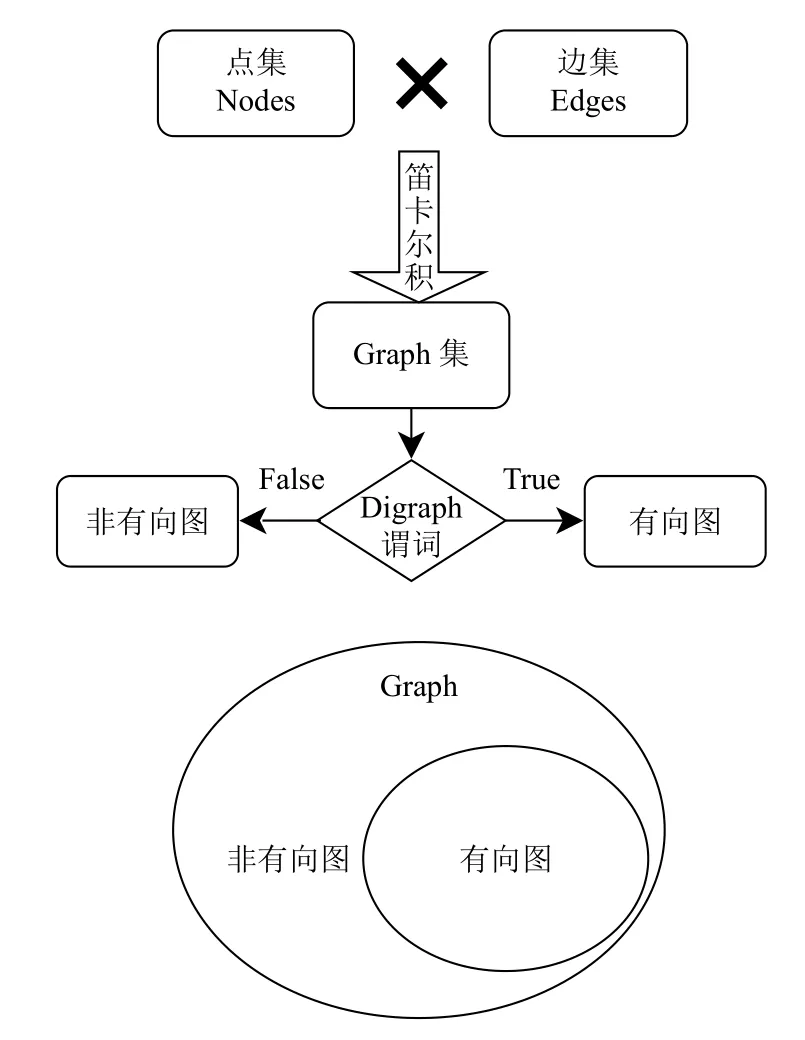
圖4 graph 類型與有向圖關(guān)系示意圖

此外,在實現(xiàn)節(jié)點的信息統(tǒng)計等功能函數(shù)時,需要遍歷一個有向圖中的所有節(jié)點.在HOL4 定理證明器使用的Standard ML 函數(shù)式語言中,沒有循環(huán)語句,取而代之的是使用遞歸的方法來實現(xiàn)循環(huán)和遍歷的效果.由于HOL4 定理庫中缺少自定義的graph 結(jié)構(gòu)的相關(guān)性質(zhì)定理,所以使用者必須手動輔助定理證明器完成終止證明.下面將詳細介紹如何使用以上給出的方法,完成圖節(jié)點遍歷遞歸函數(shù)的終止證明.

3.1 實現(xiàn)過程

首先,繼續(xù)設(shè)置終止條件切分輸入集.待實現(xiàn)的遞歸函數(shù)功能為遍歷圖中所有節(jié)點,若點集nodes為無限集,則遍歷行為無意義,故得到第2 個終止子條件:當輸入?yún)?shù)的點集nodes 不屬于有限集時將終止遞歸;若輸入為空圖,則不需要繼續(xù)遍歷,將輸出固定值,因此得到第3 個終止子條件:當輸入?yún)?shù)不屬于非空圖時將終止遞歸.通過3 個終止子條件,將輸入集切分為如圖5所示的真子集.

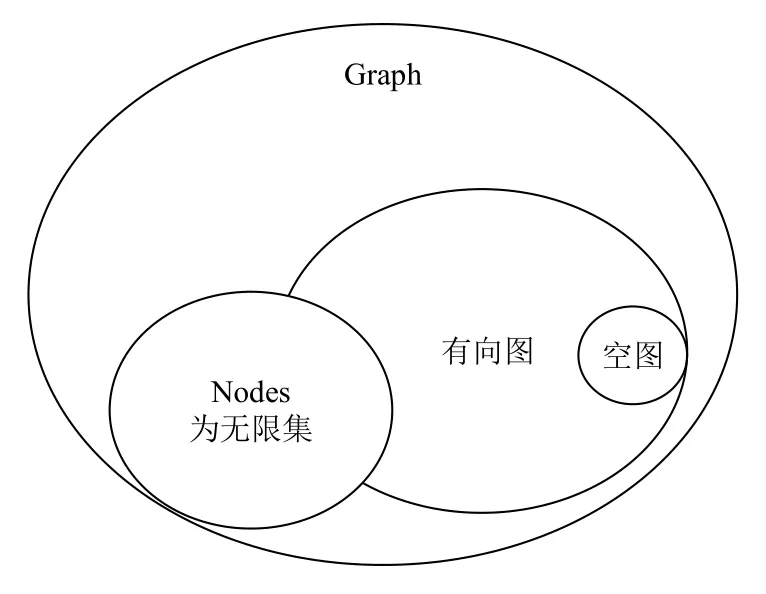
圖5 通過謂詞切割有向圖集

當輸入?yún)?shù)不僅屬于如圖所示的有向圖集合時,將終止遞歸并輸出.

終止條件的確定也明確了遞歸過程中,輸入?yún)?shù)在遞歸的過程中應(yīng)不斷趨向于終止條件.在圖節(jié)點遍歷函數(shù)中,可以將輸入的圖參數(shù)視作“已遍歷”和“未遍歷”兩部分.在遞歸過程中,“未遍歷”的部分將持續(xù)減少,在遍歷完成時“未遍歷”部分應(yīng)當為空,滿足第3 個終止子條件.因此,對于該遞歸函數(shù)的終止證明問題,應(yīng)當關(guān)注輸入?yún)?shù)“未遍歷”部分的節(jié)點規(guī)模,并定義合適圖規(guī)模量化函數(shù),設(shè)置空圖的規(guī)模為0.

在HOL4 定理證明器中,使用Hol_defn 方法和Defn.tgoal 方法可以得到終止證明目標,為了簡化目標中不必要的部分,關(guān)注于證明遞歸參數(shù)量化指標的遞減性,使用WF_REL_TAC 對策簡化目標并重寫展開自定義的函數(shù)后,得到兩個子目標.

?

查閱定理證明器中的集合定理庫可知,系統(tǒng)拋出該子目標無法繼續(xù)的原因是庫中缺少處理{x|x ∈ s ∧x≠ CHOICE s}的相關(guān)定理,需要用戶輔助證明.因此,利用定理證明器提供的集合定理庫,證明以下引理:

引理1.對于任意的集合s,由s中CHOICE s 元素以外的元素組成的新集合,等于REST s 集合.

?s.{x|x ∈ s ∧ x≠ CHOICE s}=REST s

引理2.對于任意集合s,如果s為非空有限集,則CARD s 大于0.

?s.FINITE s ∧ s≠ ? ? 0

借助引理即可完成子目標1的證明.然后關(guān)注子目標2.

?

觀察可知,系統(tǒng)拋出此目標的原因不僅是缺少子目標1中的兩個引理,而且缺少圖的相關(guān)性質(zhì)定理:當邊集非空時,點集必定非空.該定理由圖的定義與空圖的定義推導而來.

有向圖性質(zhì)1 邊集非空的有向圖點集必然非空

?G.Digraph G ∧ G.edges≠ ? ? G.nodes≠ ?

借由引理1和引理2,圖的性質(zhì)定理和定理證明器的相關(guān)定理庫,即可完成該遍歷函數(shù)的終止證明.最后將對策整理為策略,并使用Defn.tprove 方法定義該函數(shù).

在本實例中,可見使用本文提出的終止證明方法解決終止證明問題,思路非常清晰,迅速確定終止條件,補充必要的謂詞和函數(shù),將終止證明目標簡化為圖的節(jié)點數(shù)量在遞歸過程中的遞減性證明,準確找到終止證明過程中缺少的兩個集合引理和一個圖的性質(zhì)定理,順利完成終止目標的證明,解決終止證明問題,從而在HOL4中成功定義圖的節(jié)點遍歷遞歸函數(shù).

4 結(jié)語

形式化建模工作中對遞歸函數(shù)的應(yīng)用十分廣泛而且重要.由于定理證明器的定理庫更新上的嚴謹和滯后,在涉及到遞歸函數(shù)的建模過程中,特別是使用到自定義的數(shù)據(jù)結(jié)構(gòu)進行遞歸的建模中,經(jīng)常出現(xiàn)定理證明器無法自動完成終止證明的問題,導致遞歸函數(shù)無法被成功定義和使用,阻礙了形式化方法的應(yīng)用和發(fā)展.

本文針對上述問題,介紹了在形式化工作中為什么會遇到終止證明問題,以及解決終止證明問題的必要性;分析了定理證明器無法自動完成終止證明的原因;設(shè)計了一種在形式化建模中通用的終止證明方法,并將該方法應(yīng)用于基于HOL4 定理證明器的一個實例中.在不同的定理證明器中,使用的具體對策和函數(shù)有所不同,但是方法的步驟和思路是相同的,以可量化的指標作為終止條件的遞歸函數(shù)可以使用該方法進行定義并證明.該方法很大程度方便了形式化建模的初學者在定理證明器中定義和使用自己的數(shù)據(jù)結(jié)構(gòu)和遞歸函數(shù),使用形式化方法解決更具體和實際的問題.

同時,該方法尚存不足,無法解決式(2)形式的自嵌套遞歸函數(shù)的終止證明問題.