尹長明, 石岳鑫

(廣西大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,廣西 南寧 530004)

1.引言

縱向數(shù)據(jù)(集團(tuán)數(shù)據(jù), 面板數(shù)據(jù)), 經(jīng)常出現(xiàn)在生物, 醫(yī)學(xué), 經(jīng)濟(jì)和社會科學(xué)的研究中.它是對同一個個體進(jìn)行多次觀測, 所得數(shù)據(jù)是相關(guān)的, 但相關(guān)系數(shù)未知.廣義估計方程(GEE)[1]是分析縱向數(shù)據(jù)回歸問題的重要方法.GEE方法的一個顯著特點是即使每個個體多次觀測值之間的相關(guān)系數(shù)(方差)假定錯誤, 只要均值函數(shù)假定正確, 所得回歸系數(shù)的GEE估計仍具有相合性和漸近正態(tài)性.若相關(guān)系數(shù)假定也正確, 則得到的GEE估計方差最小.

設(shè)(Yij,Xij)是第i個個體的第j次觀測值,i=1,2,...,n,j=1,2,...,m, 其中Yij是響應(yīng)變量,Xij是p×1協(xié)變量,m是每個個體的觀測次數(shù).假設(shè)不同個體之間的觀測值是獨立的, 同一個個體的m次觀測值是相關(guān).記Yi= (Yi1,...,Yim)T,Xi= (Xi1,...,Xim),i= 1,...,n, 其中T表示矩陣或向量的轉(zhuǎn)置.設(shè)期望和方差分別為

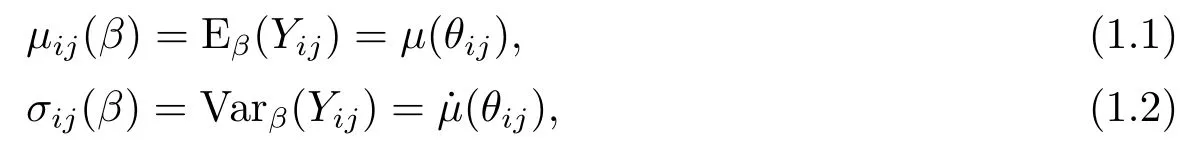
其中μ(θ)是聯(lián)系(link)函數(shù), ˙μ(θ)>0是它的導(dǎo)數(shù),θij=,β= (β1,··· ,βp)T是回歸參數(shù)向量.若μ(θ) =θ, 就得到線性回歸模型,μ(θ) = eθ/(1+eθ)就得到分析二分類數(shù)據(jù)的logistic模型,μ(θ)=eθ就得到分析計數(shù)數(shù)據(jù)的對數(shù)線性模型.

記μi(β) = (μi1(β),...,μim(β))T,Ai(β) = diag(σi1(β),...,σim(β)), 其中, diag(v)表示一個對角矩陣, 其對角元素是向量v的元素.Balan, Schiopu-Kratina[2]定義方程

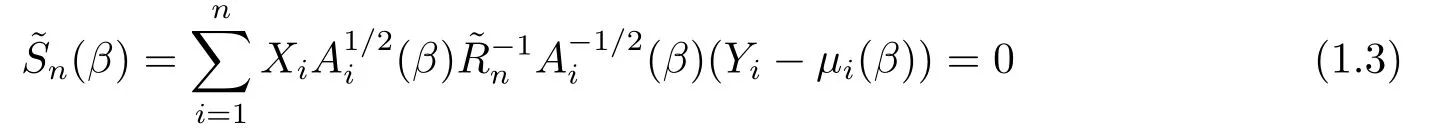
的根為GEE估計, 其中估計工作相關(guān)矩陣(estimating working correlation matrix)定義為

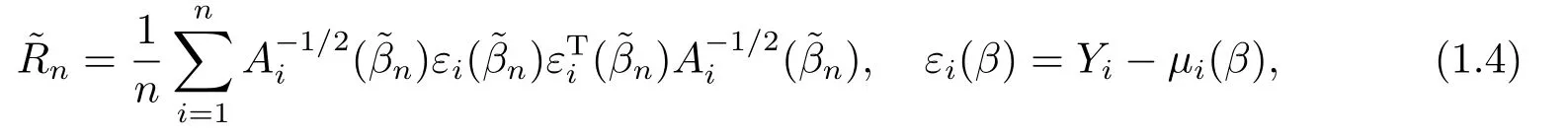
若協(xié)變量維數(shù)是發(fā)散的, 記p=pn,β=βn=(βn1,··· ,βnpn)T.WANG[3]定義方程

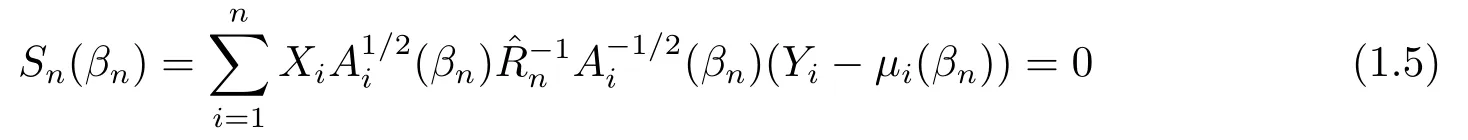
GEE的建?？蓞⒖次腫4-5].關(guān)于GEE的大樣本性質(zhì), Balan, Schiopu-Kratina[2]研究了協(xié)變量維數(shù)固定, GEE估計的相合性和漸近正態(tài)性, 未研究Wald統(tǒng)計量的漸近分布, 而漸近正態(tài)分布的方差含有未知的真實相關(guān)系數(shù), 不能直接用于區(qū)間估計和假設(shè)檢驗.WANG[3]研究了當(dāng)樣本容量趨于無窮, 協(xié)變量維數(shù)趨于無窮, GEE估計的相合性和漸近正態(tài)性.并且證明了響應(yīng)變量是兩點分布Wald統(tǒng)計量的漸近分布是卡方分布, Wald統(tǒng)計量可以直接用于統(tǒng)計推斷.本文證明了協(xié)變量維數(shù)是固定的或趨于無窮, 響應(yīng)變量是任意分布Wald統(tǒng)計量的漸近分布是卡方分布.推廣了文[2-3]中的有關(guān)結(jié)果.

2.主要結(jié)果

在本文中,C,C1,C2,...代表與n無關(guān)的正常數(shù), 在不同地方可以表示不同值.為了得到我們的主要結(jié)果, 需要如下假設(shè)條件.

引理2.1[2]當(dāng)協(xié)變量維數(shù)p固定, 若假設(shè)條件(A1)-(A5)成立, 則存在一個隨機(jī)變量序列使

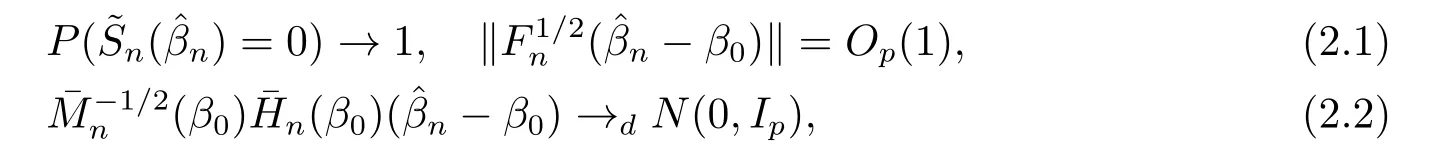
其中

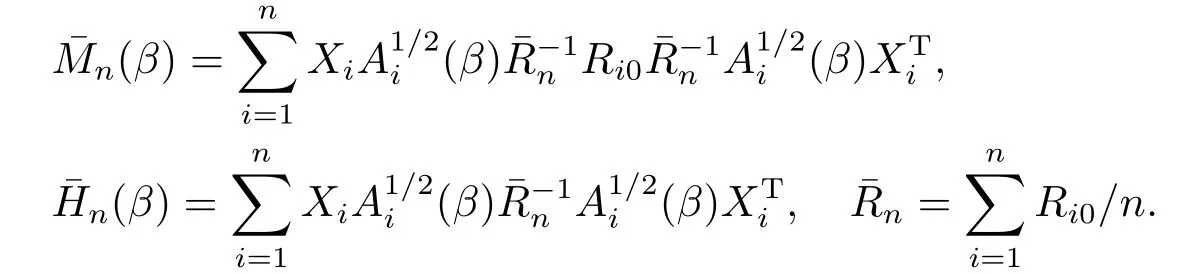
引理2.2[3]當(dāng)協(xié)變量維數(shù)p=pn趨于無窮, 若假設(shè)條件(A6)-(A12)成立, 則存在一個隨機(jī)變量序列使

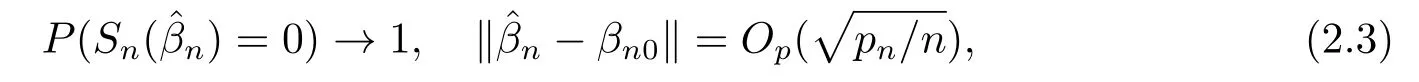
且對任意單位向量αn有

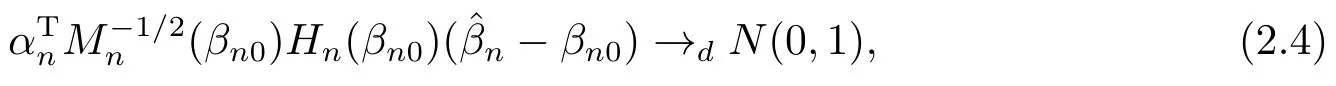
其中

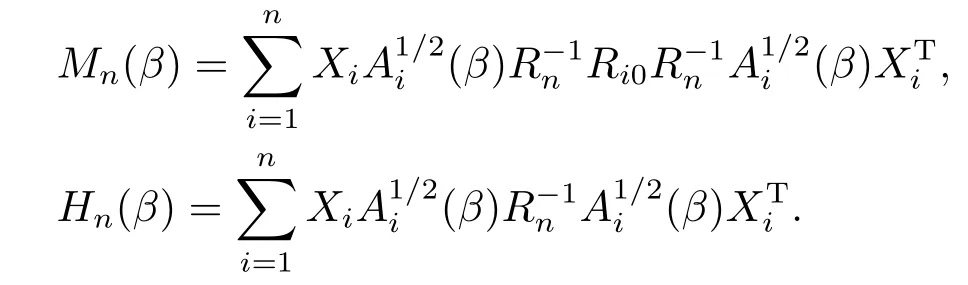
H0:Lβ0=avs.H1:Lβ0a,

其中L是l×p行滿秩矩陣,a是l×1向量.下面定理2.1可解決這些問題.

定理2.1當(dāng)協(xié)變量維數(shù)p固定, 若假設(shè)條件(A1)-(A5)成立, 則存在使(2.1)成立, 且

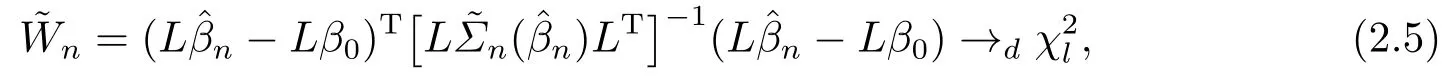
其中是自由度為l的卡方分布,

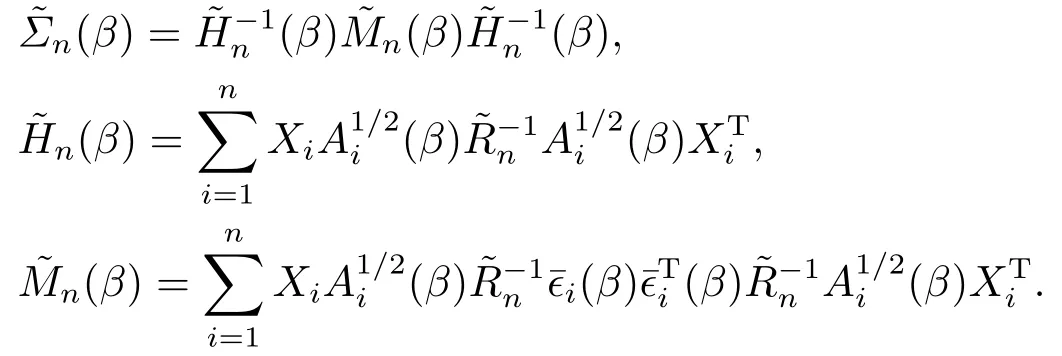
注2.1定理2.1填補(bǔ)了文[2]中關(guān)于線性假設(shè)Wald統(tǒng)計量漸近分布的一個空白.

由于引理2.2也含有未知的Rn0,βn0, 所以引理2.2也不能直接用于統(tǒng)計推斷, 而且在實際應(yīng)用也經(jīng)常需要檢驗線性假設(shè)

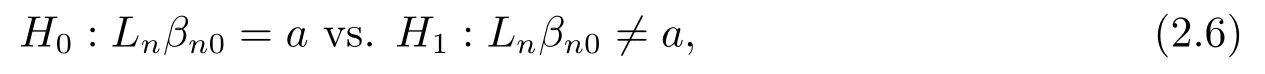
其中Ln是l×pn行滿秩矩陣,a是l×1向量.為此我們有下面定理2.2可直接用于統(tǒng)計推斷.

定理2.2當(dāng)協(xié)變量維數(shù)p=pn趨于無窮, 若假設(shè)條件(A6)-(A13)成立, 則存在使(2.3)成立, 且

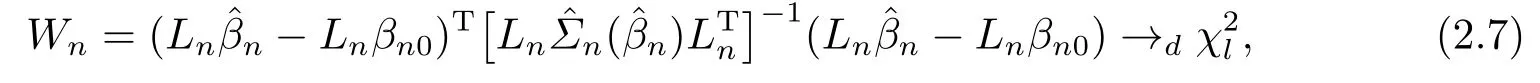
其中

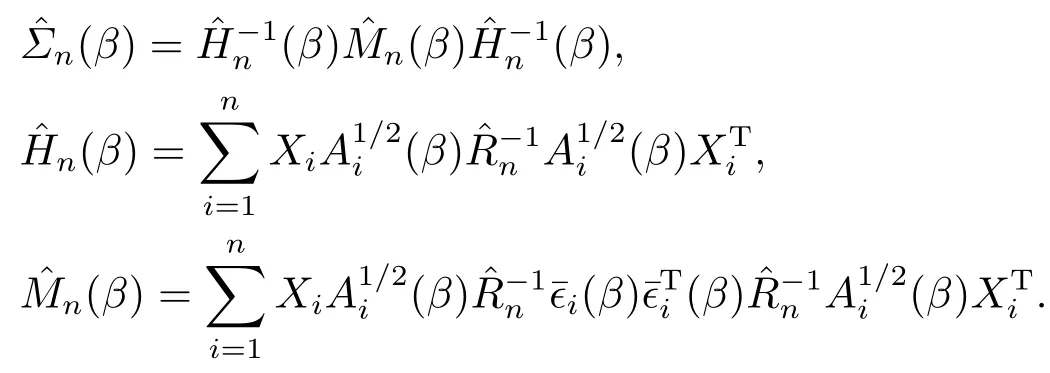
注2.2顯然定理2.2是文[3]中推論3.11的推廣, 因為0,1分布的任意階矩存在.

注2.3對對數(shù)線性Poisson模型, 定理2.2與引理2.2所需條件一樣, 因為假設(shè)(A11)可推出(A13).

3.主要結(jié)果的證明

為了證明第2節(jié)的主要結(jié)果, 我們還需要如下一些引理.

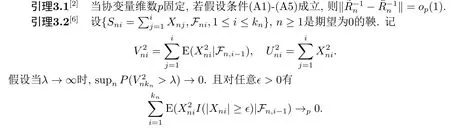
則

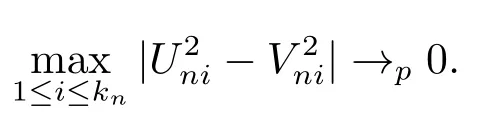
定理2.1的證明易驗證

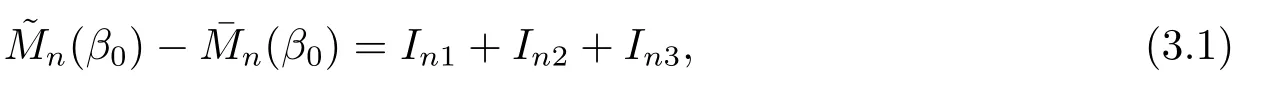
其中

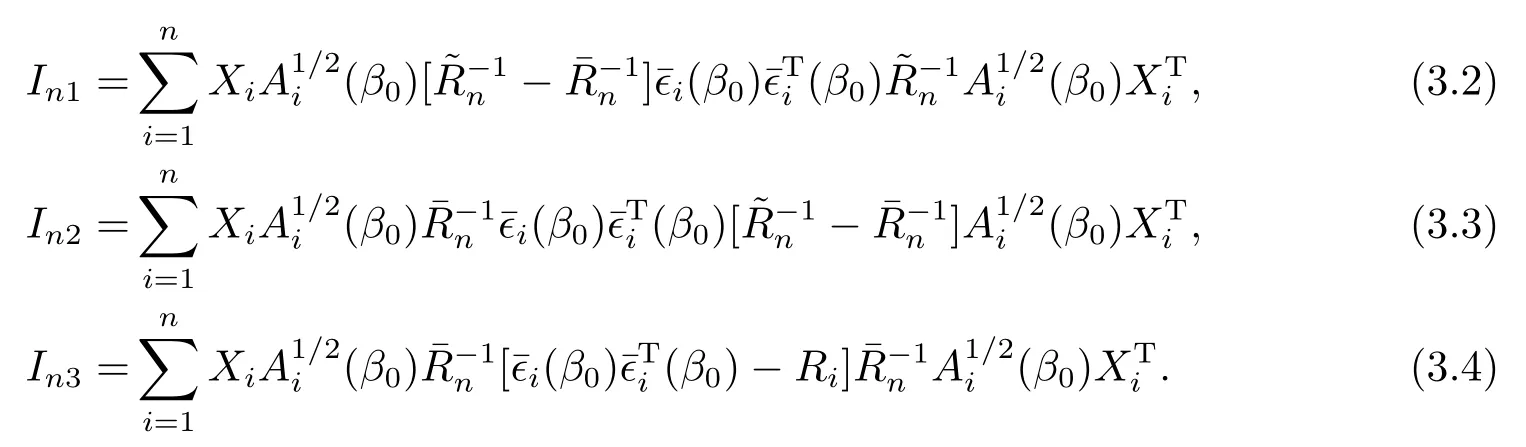
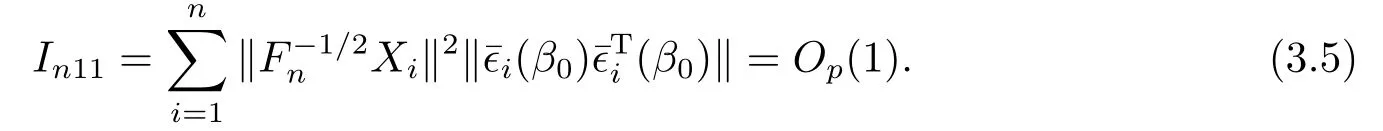
由假設(shè)(A5, (A4), 引理3.1和(3.5)式, 知=Op(1),

且

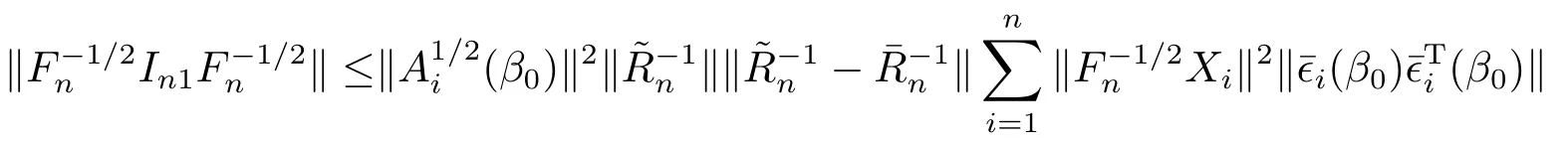
同理,

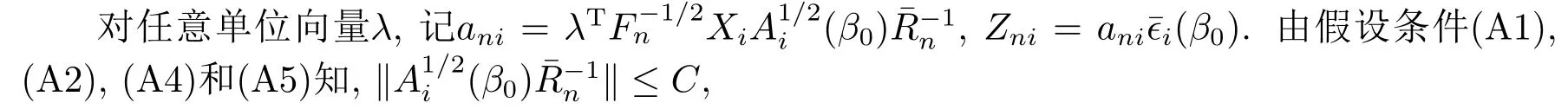
且

由假設(shè)(A2)和(3.9)式知, 對任意?,

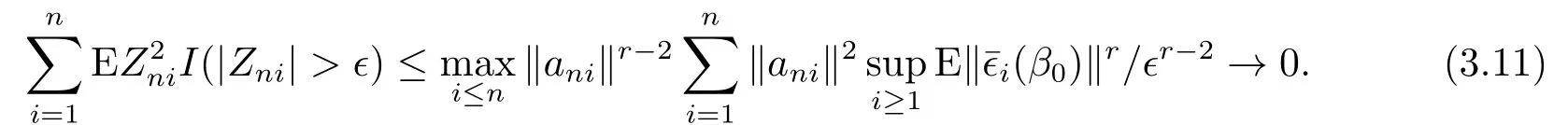
可驗證

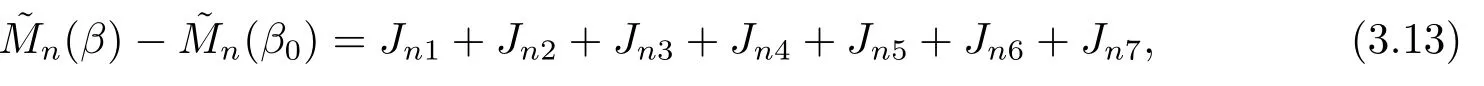
其中

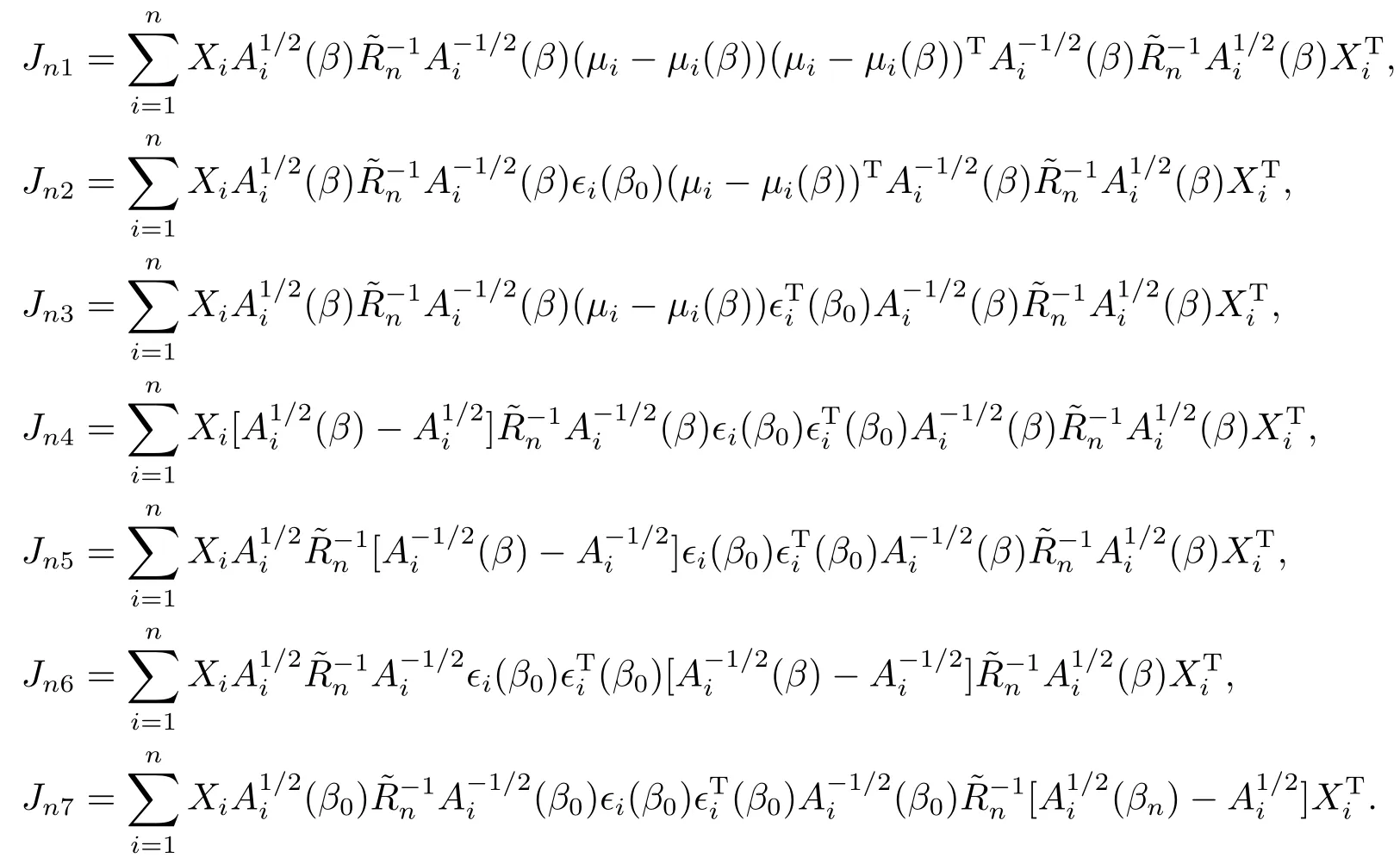
由假設(shè)(A1)知,

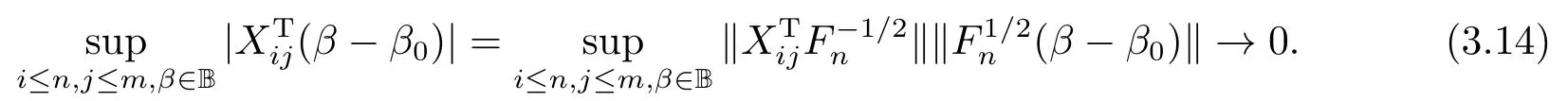
由微分中值定理, (3.14)和(A5)知, 對所有1≤i ≤n,1≤j ≤m,β ∈B,

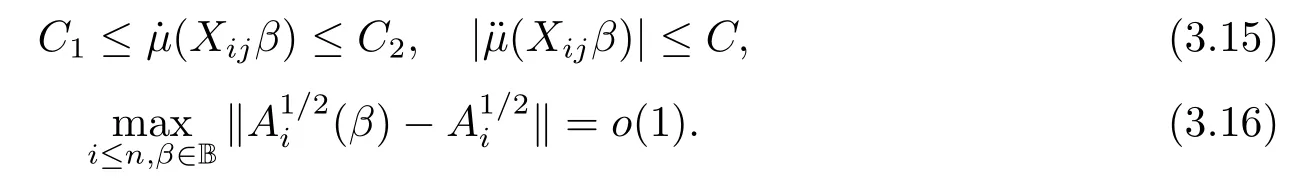
由(3.5), (3.6), (3.15)和(3.16)知,

同理

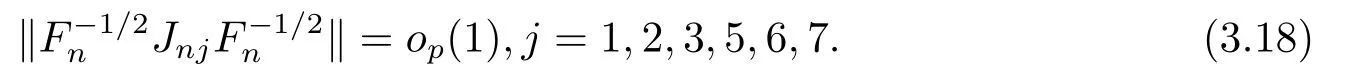
由引理3.1和(3.15)知,

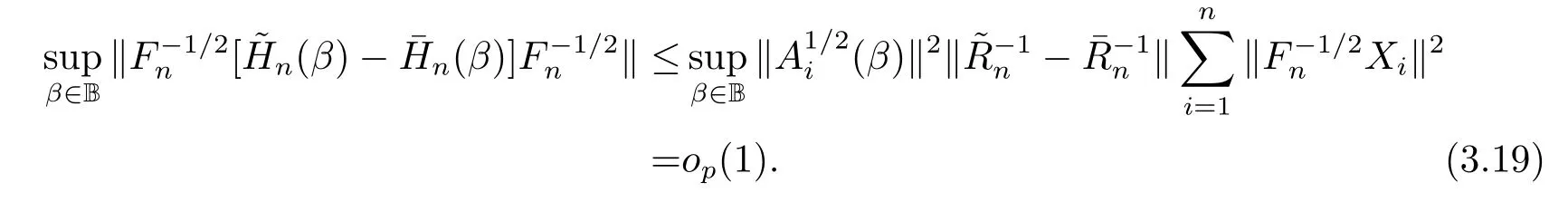
由微分中值定理, (3.15), (A4)和(3.14) 知,

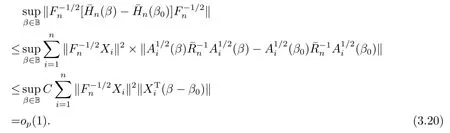
由(A4)和(A5)知,

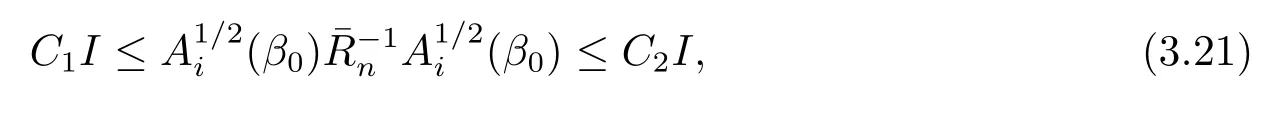
且

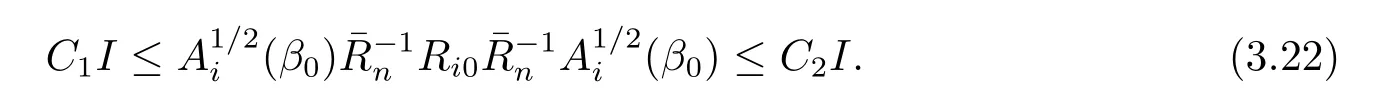
由(3.21)和(3.22)知,

由(3.1), (3.7), (3.8), (3.12), (3.14), (3.17), (3.18)和(3.23)知,

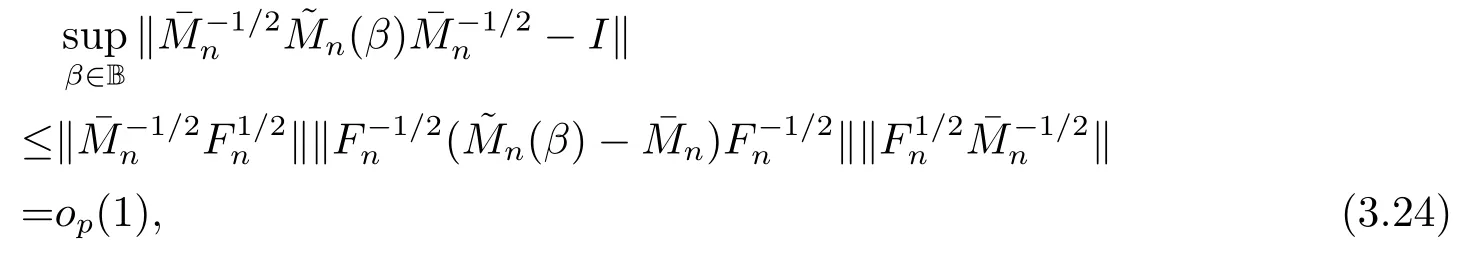
即對β ∈B,

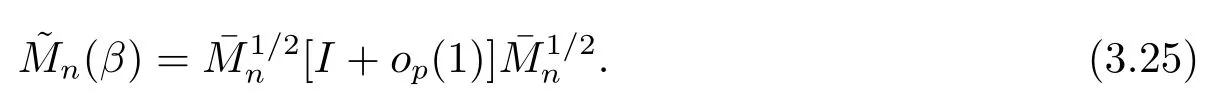
由(3.19), (3.20)和(3.23)知,

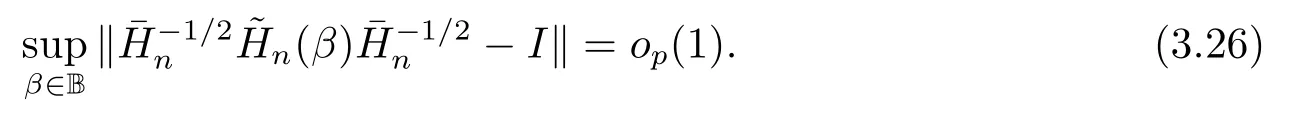
即對β ∈B,

由(3.23), (3.25)和(3.27)知, 對β ∈B,

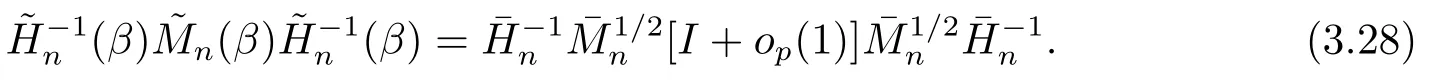
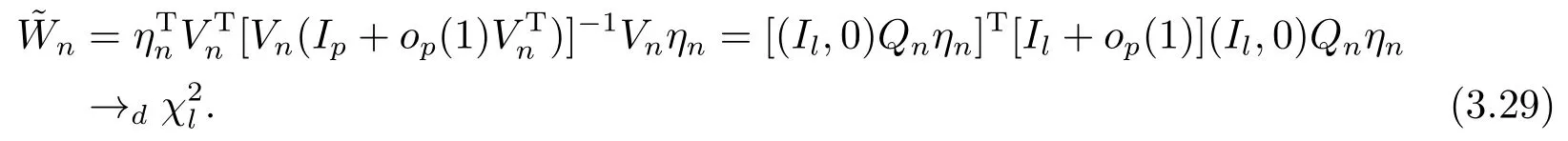
定理2.2的證明易驗證

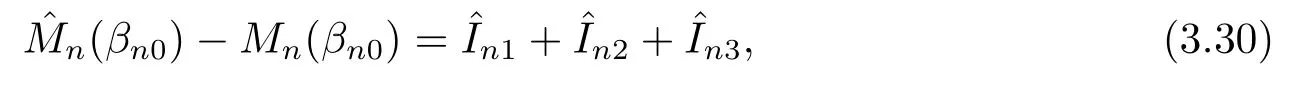
其中

由假設(shè)(A6)和(A10)知,

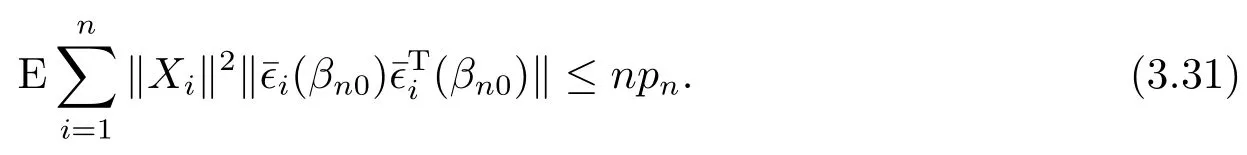
由假設(shè)(A9),(A11),(3.31)式和(A12)可得,

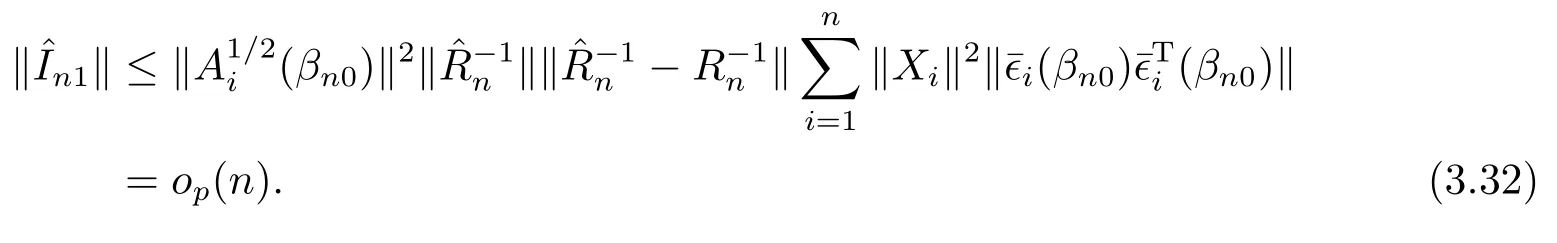
同理,

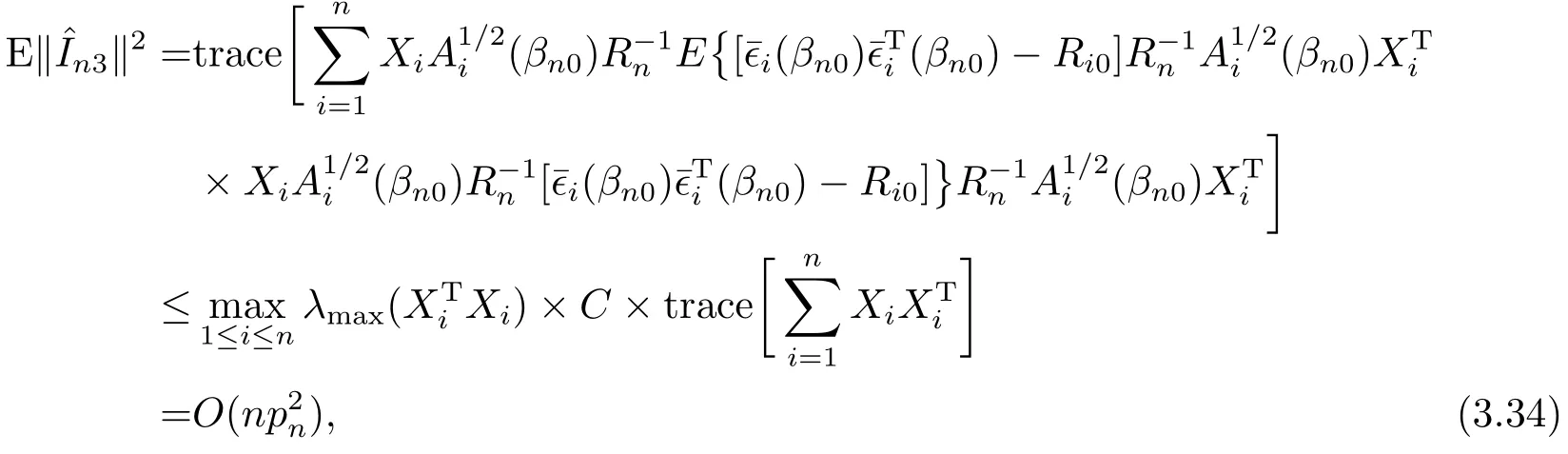
其中λmax表示矩陣的最大特征根.由(3.34)式和假設(shè)(A12)知

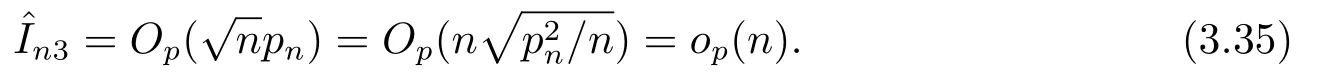
記?i(βn0)=Yi ?μi(βn0).則可驗證

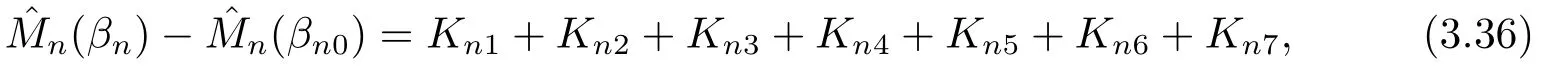
其中

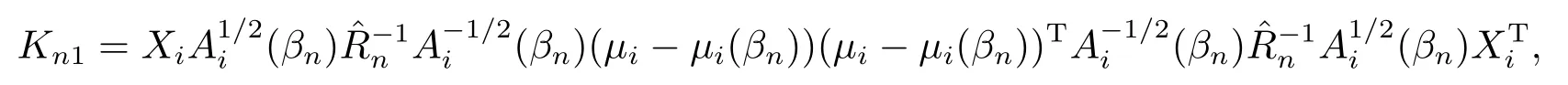
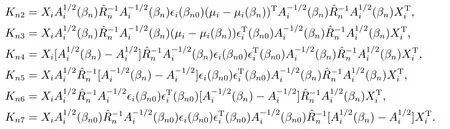
由假設(shè)(A8)和(A10)知, 對cn ∈Rpn, 有

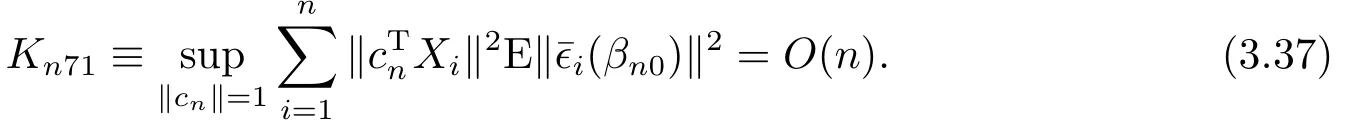
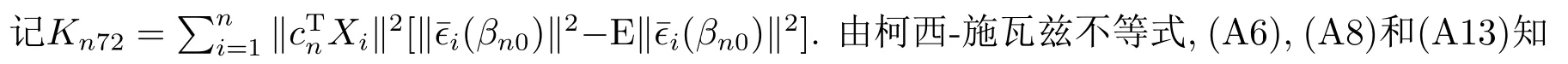
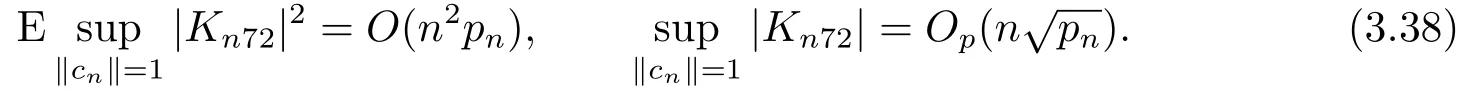
由(A11), (A9), 微分中值定理, (A6), (3.37), (3.38), (A12)可得

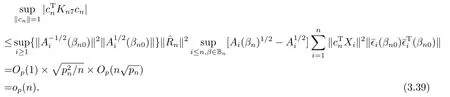
同理可證

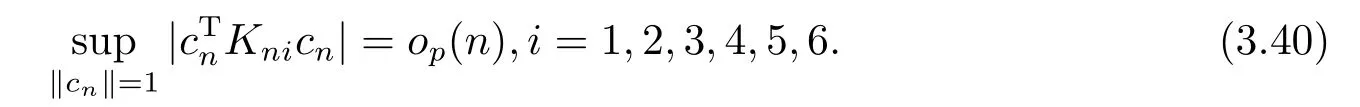
對任意an ∈Rpn,bn ∈Rpn,‖an‖=1,‖bn‖=1,由(A11), (A9), (A12), 柯西-施瓦茲不等式和(A8)知, 對βn ∈Bn有

由微分中值定理, (A11), (A9), 柯西-施瓦茲不等式, (A6), (A8), (A12)知, 對βn ∈Bn有

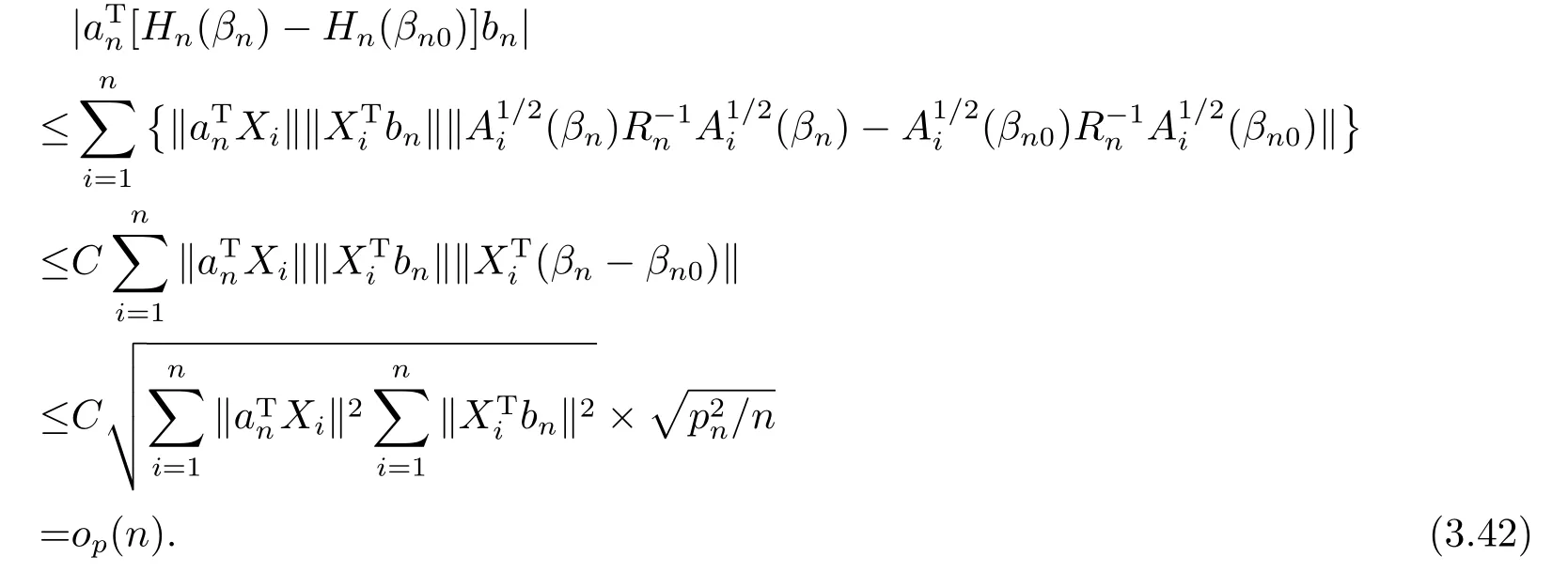
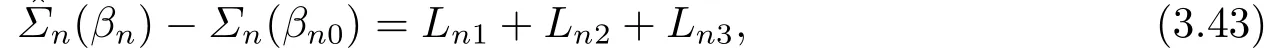
其中

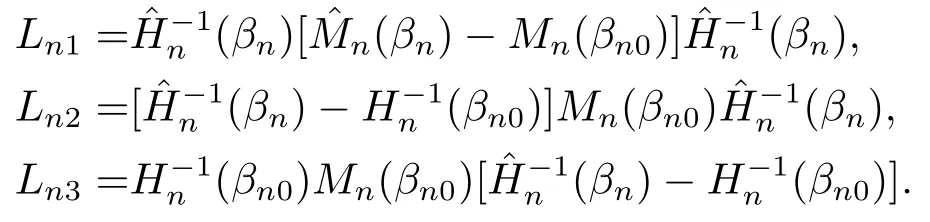
由(A9), (A11)和(A8)知,

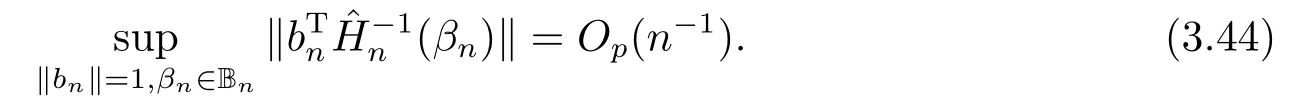
由(3.30), (3.32), (3.33), (3.35), (3.36), (3.39), (3.40)和(3.44)知

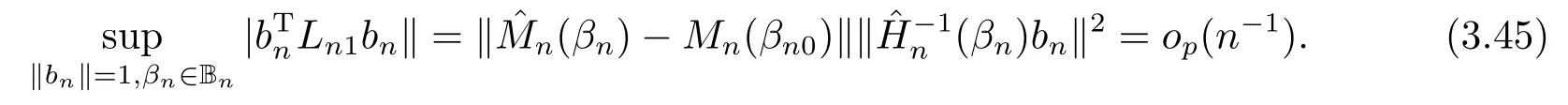
由(A9)和(A11)知,

由(3.46), (3.47)和(3.44)知,

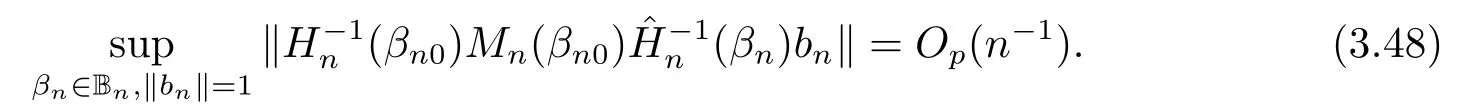
由(3.41)和(3.42)知,

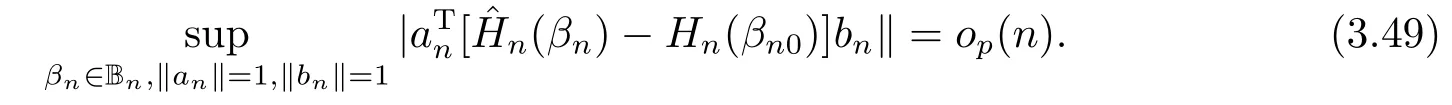
由(3.44), (3.48)和(3.49)知,

同理

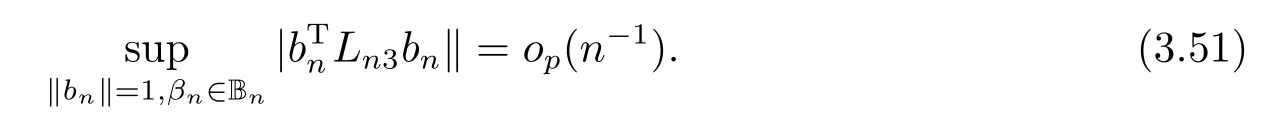
由(3.43), (3.45), (3.50)和(3.51)知,

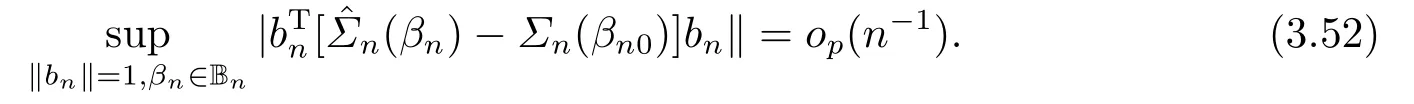
由文[7]的59頁知, 存在可逆矩陣Γn和滿足條件=Il的l×pn矩陣得

由(3.46), (3.47)和(A8)知,

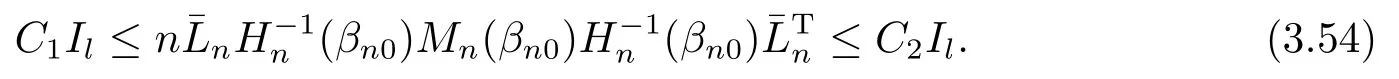
由(3.52), (3.54)和引理2.2得,

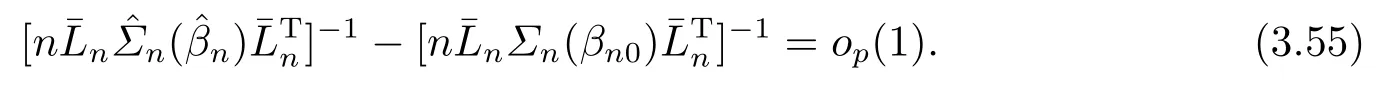
由引理2.2得,

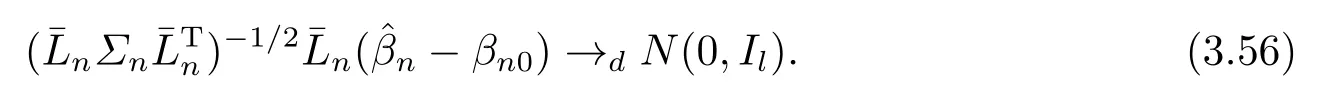
由(3.56)和(3.54)得,

由(3.53), (3.55), (3.56)和(3.57)得,

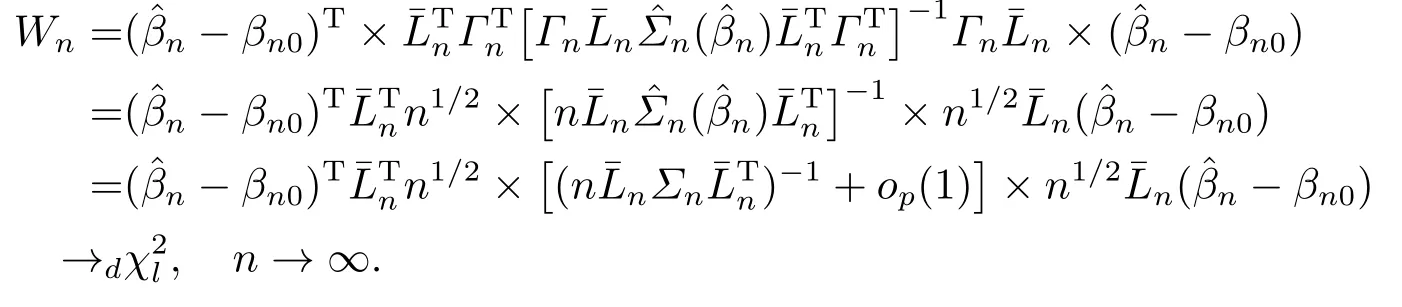
4.結(jié)語

當(dāng)文[3]中的假設(shè)成立, 即Yi,i= 1,··· ,n,有共同的真實相關(guān)陣時, 定理2.2中工作相關(guān)陣Rn可以等于真實相關(guān)陣Rn0.若相等, 則估計的漸近方差最小(證明類似文[8]).所以若定理2.2中估計工作相關(guān)陣取定理2.1中的形式, 則估計的漸近方差最小.為了節(jié)省篇幅,模擬省略.