Ling-Ling Zhang(張玲玲), Wei-Zhong Chen(陳偉中), Yao-Rong Wu(武耀蓉),Yang Shen(沈陽), and Guo-Ying Zhao(趙幗英)

Key Laboratory of Modern Acoustics(Ministry of Education),Institute of Acoustics,Nanjing University,Nanjing 210093,China

Keywords: bubble–bubble interaction,repulsion,phase shift

1. Introduction

It is a well-known phenomenon that the bubble–bubble interaction (BBI) exists between gas bubbles in an ultrasonic field,[1]and hence it is called the Bjerknes force. It is divided into the primary Bjerknes force and the secondary Bjerknes force. Both forces are related to the acoustic pressure gradient. The former is a translational force on the bubble,which originates from the fact that the acoustic pressure gradient derived from external pressure couples with the bubble oscillations.[2,3]If the bubble radius is larger than the resonant radius,the bubble travels toward a pressure node. Otherwise,the bubble moves toward a pressure anti-node. The pulsating bubbles emit the secondary acoustic field and will exert radiation force on other bubbles,and the radiation force is averaged over period,that is,the secondary Bjerknes force.[4–6]The direction of the force represents the attraction or rejection of bubbles. According to the classical Bjerknes theory based on linear dynamics,the force between two bubbles is repulsive if the driving frequency lies between their resonance frequencies,otherwise it is attractive.[7–9]

As is well known, the bubble pulsation is no longer linear in actual ultrasonic field, so that the radiation force between two bubbles due to the secondary sound fields emitted by other pulsating bubbles has been absorbing researchers’attention,[10–17]and the direction of the force becomes a research hot point.[18–21]Mettinet al.[22]concluded that the force between two bubbles is symmetric, similar to the action and reaction, and their strengths and directions differ considerably from predictions by the linear theory, under the assumptions of periodic pulsation and negligible translation.Doinikov[23,24]considered both radial pulsation and central translation of two bubbles and simulated their many interesting behaviors in strong acoustic fields,such as self-propulsion of a bubble pair. Oguz and Prosperetti[25]obtained that in certain parameter ranges the force between the bubbles has a sign opposite to what is expected on the basis of the linear theory of Bjerknes forces. Harkin[26]studied the coupled pulsation and translation of two gas bubbles in weak amplitude acoustic forcing and also in moderate amplitude acoustic forcing.In these calculations, the BBI is attractive in most cases, but also repulsive in some cases. In this paper, the three specific mechanisms of repulsive BBI and the evolution of the BBI in ambient radius space are investigated in liquid driven by ultrasound. The rest of this paper is organized as follows. In Section 2,the specific expression of the radiation force is given.In Section 3, the mechanism of the repulsive BBI for pairs with different bubble radii is analyzed and the distribution of the BBI in ambient radius space is simulated numerically. In Section 4,the BBIs at different distances between the bubbles are discussed. And some conclusions are drawn from this present study and discussion is also present in Section 5.

2. Bubble–bubble interaction

Assuming that a spherical bubble 1 with radiusR1is located atx1and accompanied by the other spherical bubble 2 with radiusR2located atx2on thexaxis in an incompressible fluid with densityρ,then the force acting on the surface of the bubble 1 by the radiation sound field of the bubble 2 will be written as[1]

withexbeing the unit vector fromx1tox2andF1changes with time and may alternate between positive and negative.Averaging Eq. (4) over an intervalτ, such as an acoustic period,one obtains the BBI acting on bubble 1 from bubble 2 as follows:[7]

If the weighted ratio of the negativeF1to positiveF1is greater than 1 in an acoustic period,theFB1is negative,which means that bubble 1 moves away from bubble 2. The BBI is repulsive. Otherwise, the bubble 1 moves toward bubble 2. The radiiR1andR2,and locationsx1andx2,of course,obey their dynamic equations including two pulsation equations and two translation equations according to the Doinikov equations(see Appendix A).

3. Repulsive bubble–bubble interaction

As is well known,when the ambient radii of two bubbles are the same,the BBI is always attractive. However,the ambient radii of bubbles in acoustic field are not of the same size,and there is a size distribution. The evolution profile including the locations of the peak and rebound radius is different for different bubbles. As a result, the BBI cannot always be attractive. The following are three mechanisms of bubble repulsion. The MATLAB program package is used to analyze the mechanism of the repulsive BBI for pairs with different bubble radii and to simulate numerically the distribution of BBI.We set the physical parameters to bep0=1 bar(1 bar=105Pa),ρ=998 kg/m,c=1500 m/s,κ=1.4,σ=0.0725 N/m,andη=0.001 Pa·s.

3.1. “Elastic”bubble and“inelastic”bubble

The pulsating bubble dynamics shows that a bubble will pulsate with weak rebound under a strong driving sound at a suitable frequency,such as a sonoluminescing bubble. On the contrary, the bubble will rebound strongly when the driving sound is weak or when the driving frequency is not appropriate. The strong rebound is similar to the elastic collision in mechanics and the weak rebound to the inelastic collision,so that the strong rebound bubble (weak rebound bubble) is referred to as “elastic” bubble (“inelastic” bubble), hereinafter.Of course,the boundary between“elastic”bubble and“inelastic”bubble is not clear,similar to that between the elastic ball and inelastic ball in mechanics. The radiation force on an“inelastic”bubble due to the pulsation of the other“elastic”bubble is considered now.

Fig.1. Pulsation and BBI of“inelastic”bubble accompanied with an“elastic” bubble, showing (a) radius curves, and (b) instant force (solid curve)and negative force of“inelastic”bubble(dot-dashed line)with driven sound being 1.3 bar in amplitude at frequency 25 kHz,and the ambient radii being 4μm and 2μm,respectively.

Here, we investigate case A. The bubbles with different ambient radii pulsate in different amplitudes under a given ultrasound. Bubble 1 in Fig. 1(a) pulsates in “inelastic” style,and bubble 2 in “elastic” style. There is a phase shift ?φbetween them (see Fig. 1(a)). Obviously, two bubbles with the same ambient radii will pulsate exactly identically,that is,?φ=0,and the BBI is always attractive,that is,FB1>0.If ?φis large enough,theFB1can change from positive to negative(Fig.1(b)). On the other hand,the BBI can also change into a repulsive interaction as the distance between bubbles changes as shown in Ref. [22]. Figure 1(b) shows that the rebound points of bubble 2 catch the large radius of bubble 1, which makes a great contribution to the negative radiation force. In order to understand the dependence of the radiation force on bubble size,theFB1in the ambient radius space is calculated.

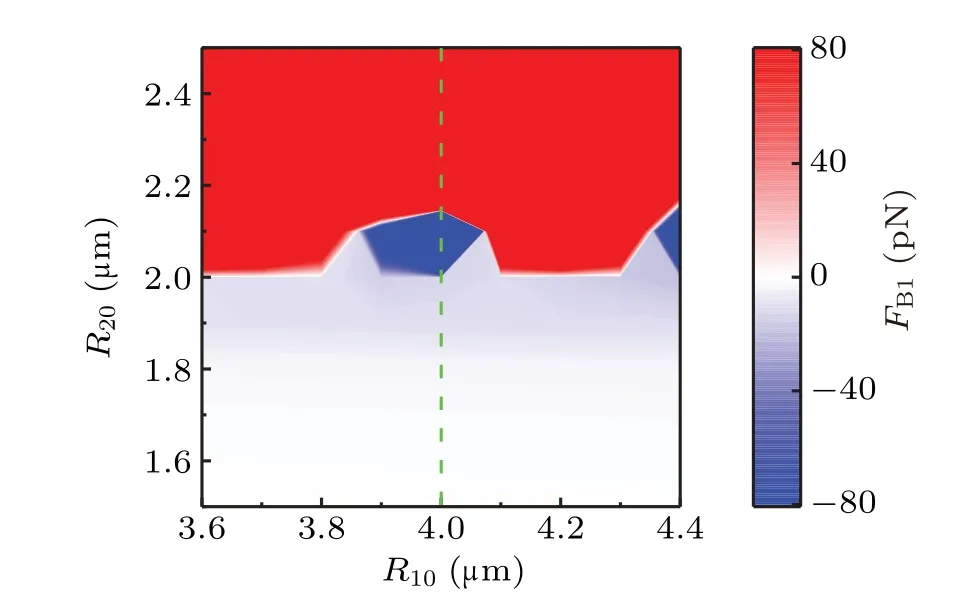
Fig.2. Distribution of BBI for“inelastic”bubble and“elastic”bubble,with driven sound being the same as that in Fig.1.

The result is shown in Fig. 2, where the red region and blue region show the attractive and repulsive BBI,respectively.For each ambient radius of bubble 1, a repulsive BBI can be obtained by choosing a small bubble 2, such as smaller than 2.0 μm. Furthermore, the repulsion from bubble 2 will be maintained as bubble 2 turns smaller and smaller,that is,coming down along the vertical dashed line in Fig.2.

3.2. Both“elastic”bubbles

Then, we study case B.As shown in Figs.3(a)and 3(c),two bubbles pulsate in an “elastic” style with a small phase shift ?φ,where the strong rebound lasts a quite long time.TheFB1can be negative (Fig. 3(b)) when some rebounds of bubble 2 just meet the large radius of bubble 1(Fig.3(a)). If the phase shift ?φincreases further as shown in Fig. 3(c), however,some rebounds of bubble 2 mismatch the large radius of bubble 1,even meet its rebounds.As a result,the BBI changes from repulsive to attractive again (Fig. 3(d)). Similarly, theFB1in ambient radius space is also plotted in Fig. 4. For a given ambient radius of the bubble 1,R10=9.3μm for example, the BBI will alternate between attractive interaction and repulsive interaction as bubble 2 becomes larger along the vertical dashed line in Fig.4. Therefore,the BBI is complex and sensitive to the ambient radius of the bubble and the accompanying bubble.

Fig.3. Pulsation and BBI of“elastic”bubble accompanied with other“elastic”bubble,showing radius curves of bubble 1 and bubble 2 with(a)9.2μm and 9.9μm and(c)9.2μm and 12.1μm,respectively,and their corresponding((b)(d))instant force(solid curve)and negative BBI of“elastic”bubble(dot-dashed line),at driven sound of 1.05 bar in amplitude at frequency 50 kHz.

Fig. 4. Distribution of BBI both “elastic” bubbles, with the same driven sound as that in Fig.3.

3.3. Stimulating bubble and stimulated bubble

Finally,we examine case C.A large bubble 1 with a small accompanying bubble 2 is assumed to be in an ultrasonic field,such as the ambient radii of large and small bubbles being 14.2 μm and 1.5 μm, respectively. The ultrasound at frequency 25 kHz excites the bubble 1 to a strong rebound,thus making the bubble 1 an “elastic” bubble (see solid curve in Fig. 5(a)) and turning bubble 2 worse than bubble 1. Therefore,bubble 2 pulsates extremely weakly and the radius evolution curve of bubble 2 is almost linear(see dot-dashed curve in Fig.5(a)). Fortunately,the collapse of bubble 1 near rebound point excites many harmonics at high frequencies and radiates the secondary pressure in liquid.The high-frequency radiation pressure generated by bubble 1 drives bubble 2 efficiently and excites its high-frequency pulsation(see Fig.5(a)).Obviously,bubble 1 acts as a stimulating bubble while bubble 2 behaves as a stimulated one.In other words,the ultrasound causes bubble 1 to pulsate,and the pulsation of bubble 1 induces bubble 2 to pulsate,so that bubble 1 plays an important role in the pulsating of bubble 2, which is quite different from both case A and case B above.

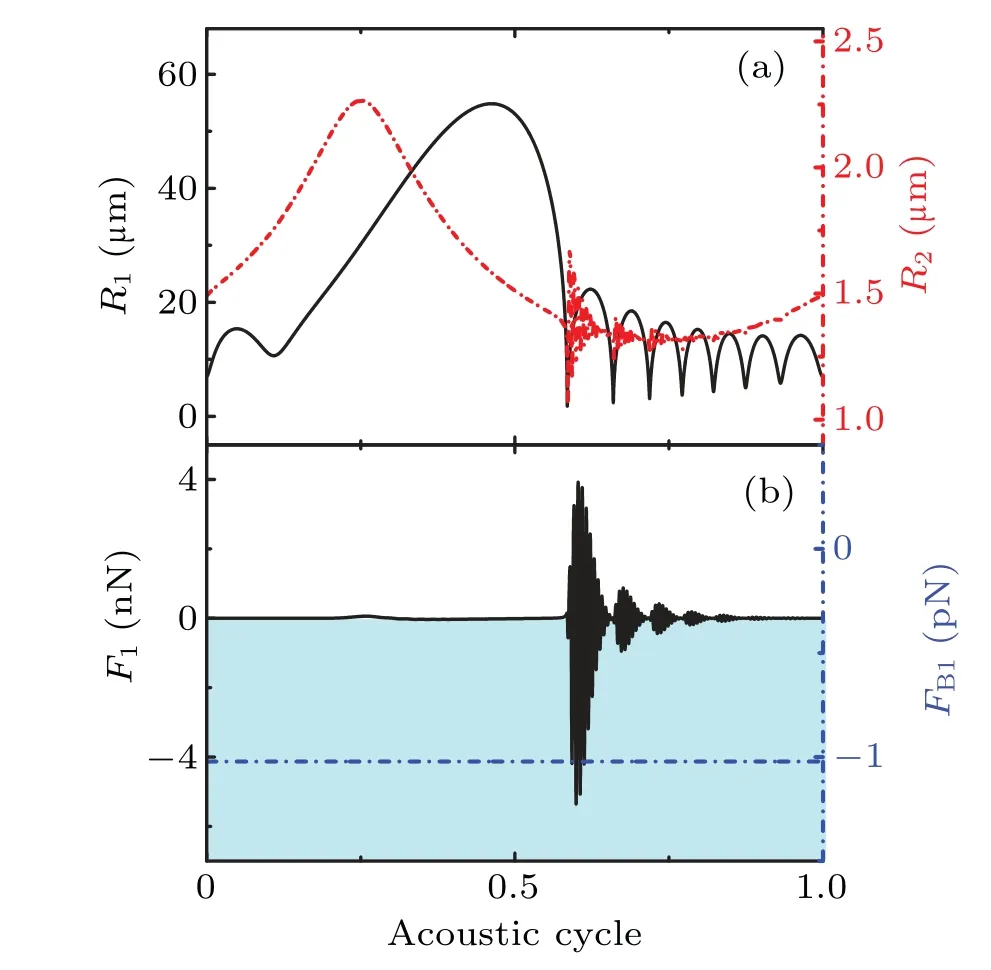
Fig.5. Pulsation and BBI of stimulating bubble accompanied with a stimulated bubble,showing(a)radius curves,(b)instant force curve(solid)and negative BBI of stimulating bubble (dot-dashed line), with driven sound being 1.3 bar in amplitude at frequency 25 kHz, and ambient radii being 14.2μm and 1.5μm,respectively.

The radiation pressure from the stimulated bubble is alternative,so that the radiation forceF1on the stimulating bubble is also alternative (Fig. 5(b)). The calculation shows that theFB1can also be negative, which means that the stimulating bubble is repelled by the stimulated bubble(Fig.5(b)). Of course,it can also be positive and the property of the BBI depends on ambient radii of two bubbles.

Figure 6 shows the distribution of the BBI in ambient radius space. For a given ambient radius of stimulating bubble,R10=14.2μm for example,the BBI will change from attractive interaction to repulsive interaction as the stimulated bubble becomes larger along the vertical dashed line in Fig.6.It is worth pointing out that the pulsating style of the bubbles will change from this case to the first case(i.e.case A)above when the ambient radius of the bubble 2 goes up through the horizontal dot-dashed line in Fig. 6, although the repulsive BBI will be maintained

To sum up,the repulsive BBI can be obtained in the three cases.The interaction picture can be switched among the three cases by changing the ambient radii of bubbles. For example,bubble 1 is set to be an “elastic” bubble. If bubble 2 is very small and serves as a stimulated bubble,the interaction picture belongs to the third case. If bubble 2 becomes large, bubble 2 will respond well to the driving ultrasound and can be considered as an “inelastic” bubble, leading the picture to be the first case. If bubble 2 becomes further larger,it will be also an“elastic”bubble,belonging to the second case.

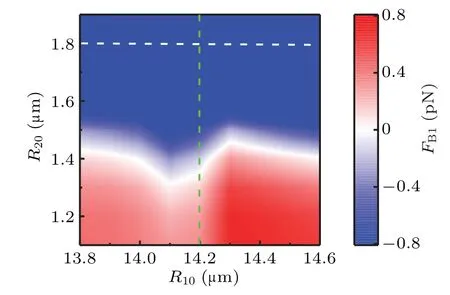
Fig. 6. Distribution of BBI of stimulating and stimulated bubbles with the same driven sound as that in Fig.5.

4. BBIs at different distances

In the calculation of this paper, the bubble translation is considered. Both the distance between the bubbles and the radii of the bubbles vary with time, and so does the BBI.We discuss the BBIs at different distances now. In Fig. 7, we record the BBIs at different distances started at the same initial distance. The variation tendency of the BBIversusthe distance, of course, is related to the parameters, such as the ambient radii,R10andR20.

When the BBI is attractive (repulsive), the distance becomes smaller and smaller(larger and larger)over time. The relation between the BBI and the distance is shown in Fig.7.It is seen from Fig. 7(a) that as the distance decreases with time increasing, the absolute value of the BBI increases. In Fig. 7(b), as the distance increases with time increasing, the absolute value of the BBI decreases.

Fig.7.BBIs at different distances where initial distance is set to be 1000μm,ambient radii of two bubbles are (a) 9.2 μm, 12 μm, (b) 9.25 μm, 10 μm,respectively,driven sound is 1.05 bar in amplitude at frequency 50 kHz,and arrows mean direction of time increasing.

Figure 8 shows the change of the BBI and the distance with acoustic period. The distance between the bubbles generally decreases with acoustic cycle number (fluctuation) increasing in a small range in Fig.8(a),and the BBI oscillates in Fig. 8(b). The repulsive BBI causes the distance to increase,which in turn forms the attractive BBI, then the distance decreases,which in turn forms the repulsive BBI.In other words,the BBI can oscillate not only in strength but also in polarity when the distance fluctuates. The BBI is very sensitive to the distance in this case.

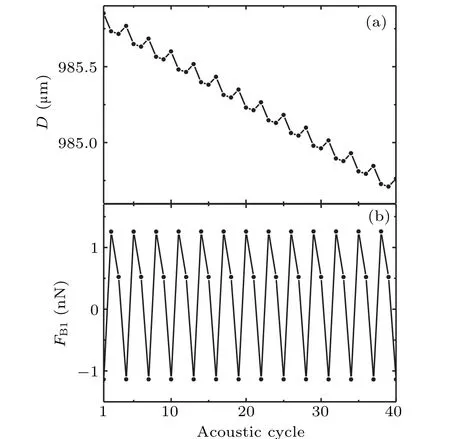
Fig.8. BBI and distance between bubbles varying with acoustic cycle number,where initial distance is set to be 1000μm,ambient radii of two bubbles are 9.2μm and 10.7μm,respectively driven sound is 1.05 bar in amplitude at frequency 50 kHz.

In a word, as the distance increases or decreases monotonically with time, the absolute value of the BBI decreases or increases, respectively. The BBI can oscillate not only in strength but also in polarity when the distance fluctuates with time.

5. Conclusions and discussion

In this paper, three specific repulsion mechanisms are given. The great contribution to the repulsive BBI originates from the large radius of the bubble catching the rebound point of the other bubble. For“elastic”bubble and“inelastic”bubble,with the increase of the phase shift between two bubbles,the BBI changes from attraction to repulsion. The repulsion from the“inelastic”bubble will be maintained as the ambient radius of the“inelastic”bubble becomes smaller and smaller.For both“elastic”bubbles,if the phase shift increases further,the BBI can change from repulsive to attractive again,that is,the BBI can alternate between attractive interaction and repulsive interaction along the direction where the ambient radius of one of bubbles continues to increase.This is different from the case of“elastic”bubble and“inelastic”bubble. For stimulating bubble and stimulated bubble,the pulsation of one bubble is completely influenced by the other bubble pulsation. The BBI can also be repulsive. Of course, it can also be attractive and its property of the BBI depends on ambient radii of two bubbles. The interaction picture can be switched among the three cases by changing the ambient radii of bubbles. In addition, the distribution of the BBI in ambient radius space shows that the BBI is sensitive to the size of bubble because the bubbles are not of the same size.Finally,when the distance increases or decreases monotonically with time, the absolute value of the BBI decreases or increases, respectively. When the distance fluctuates with time, the BBI oscillates not only in strength but also in polarity. To sum up, the BBI is very complex in a cavitation cloud.[27–29]

whereRiis the ambient radius of thei-th bubble,cis the speed of sound in liquid,Dis the time-dependent distance between bubbles’centers,overdot denotes the time derivative,κis the polytropic exponent of the gas inside bubble,σis the surface tension between the liquid and gas,fxiis the viscous drag,[30]pais the amplitude of the driving sound pressure,andηis the viscosity of the liquid.