High winding number of topological phase in non-unitary periodic quantum walk?
Yali Jia(賈雅利) and Zhi-Jian Li(李志堅(jiān))
Institute of Theoretical Physics,Shanxi University,Taiyuan 030006,China
Keywords: periodic quantum walk,high winding number,edge states
1. Introduction
Quantum walks (QWs) are the quantum analog of classical random walks,[1–3]where a walker propagates on a lattice and the direction of propagation is conditioned over the state of its coin. Compared with classical random walks,the mutual interference enhancement or cancellation of QWs on different propagating paths makes it exhibit many different dynamic behaviors,[2]for example, a quadratically fast spread of the walker over the lattice. Based on its superiorities,QWs are widely used in quantum computation,[4]quantum search algorithms,[5]quantum simulations,[6]and quantum state transfer.[7]
More recently, it is shown that a QW is a versatile simulator of some novel phenomena observed in condensed matter physics.[8]Particularly, the realization of topological phase using a discrete-time quantum walk has aroused great interests.[9–12]On aspects of experiments,QWs have been implemented in many physical systems such as nuclear magnetic resonance,[13–15]trapped atoms[16,17]and integrated optics.[18]Among of them,photonic quantum walks[19–21]offer a versatile platform to explore topological phenomena in the context of non-unitary dynamics due to the ease of adjusting gain and loss.[22–24]PT-symmetric QWs with alternating gain and loss have been investigated.[25–27]
For a Hermitian system,some states appearing in a band gap are the edge states at the boundary of two deferent topological phase regions. The bulk–edge correspondence predicts that the number of edge states is equal to the difference of topological numbers in two regions.[28,29]In non-Hermitian systems,however,the bulk–edge correspondence needs to further verify because two kinds of band gaps, point and line gaps,appear for complex energy.[30,31]Moreover,the enlarged symmetries in non-Hermitian systems also affect bulk–edge correspondence. In this work,we classify a multi-period QW with PT-symmetry into an odd-period QW and an even-period QW,and demonstrate the validity of the bulk–edge correspondence for the system with large winding number.
2. Periodic quantum walk
A discrete time quantum walk over a one-dimensional lattice is dominated by a time-evolution operatorU,which is implemented by a concatenation of coin operationCand successive position shiftS.[2]It takes place in the Hilbert space?P ??C, where the position Hilbert?Pis spanned by the position basis states{|x〉,x ∈Z}, and the coin Hilbert space?Cis spanned by the coin basis states{|↑〉,|↓〉}. Generally,the coin operator has the formC=Ix ?R(θ), whereIxis the unit operator, andR(θ) is the rotation operator in inner coin space,

The shift operatorSthat translates the particle to the left and/or right conditioned on the internal state of the particles has the form

A single step time evolution operator is given by

and the state of quantum walker aftertsteps can be expressed as

for a given initial state|Ψ(0)〉. The major point of difference between the classical and quantum implementations of the discrete time walk is the use of a quantum,rather than classical,coin operator with the result that the walker now has the possibility of being in a superposition of possible coin states|↑〉and|↓〉at every step.
The periodic quantum walk is defined by using two coin operatorsC(θ1)andC(θ2). The single step evolution operator of the two-period quantum walk is

The periodic quantum walk defined above can be realized in a quantum optical system,where the walker is shifted more than twice at each time step.[32]However, the optical signal in an optical system will experience gain or loss.[33]Thus,we introduce the gain and loss operator as follows:

TheGis a non-unitary operator whenγ/=0,and consequently the time evolution operatorUmbecomes non-unitary. Ifγ>0,the non-unitary describes an amplified process for the walker’s amplitude with coin state|↑〉and a simultaneously decayed process with coin state|↓〉.G?1has the reverse action with respect withG;γis called the degree of non-unitary since the strength of amplification or loss increases asγbecomes larger and larger.
3. Topological properties of the non-unitary periodic quantum walk with PT symmetry
The topological phase for non-Hermitian Hamiltonians,especially with PT symmetry, has become a rapidly growing research field in the recent years.[10]A non-unitary twoperiod QW as a quantum simulator has been used to study the edge states of open quantum systems. In this paper, we focus on the topological phenomena of multi-period QWs with PT-symmetry.
3.1. Dispersion relation
Since the operator ?Umhas translation invariance,performing the Fourier transform, ?Umin the momentum space is diagonal,

whereσi(i=x,y,z) is the Pauli matrix, which is a twodimensional identity matrix. From ?Um(k) ?U?1m(k)=1,we get that the coefficientsdmj(k) (j=0,1,2,3)satisfy the relation

withKbeing the complex conjugation operator. We state that an eigenstate of the PT-symmetry time evolution operator ?U′m(k) spontaneously breaks PT-symmetry if it is not the eigenstate of the PT operator. In the PT-symmetry regime,the quasi-energy are real and|λ|=1.[34]Otherwise,some quasienergy becomes complex and|λ|/=1 in the PT-symmetry broken regime.
In the following we use three-period and four-period QWs as an example to investigate the topological properties of the odd-period and even-period QWs. After some calculation,we obtain the coefficientsdmjin Eq.(11)as follows:



Whenγ= 0.1, Figs. 1(a)–1(d) and 1(e)–1(h) present the energy dispersion relations under different coin parameters(θ1,θ2) for the non-unitary three-period QW and the fourperiod QW,respectively. The real part ofEmis shown by the black solid curves and its imaginary part is shown by the red dashed curves. As shown in Figs. 1(a), 1(b), and 1(e), the quasi-energy is real and the gap does not close. The eigenstate of the non-unitary time evolution preserves PT symmetry. However, in Figs. 1(c)–1(d), the quasi-energy becomes complex at some values of momentum,at which the eigenstate breaks PT symmetry. Correspondingly,the gap of the real part closes into a line segment with Re(E3)=0 andπ.The number of gap-closed line segments with Re(E3)=0 is equal to that with Re(E3)=π. The above situation can also appear for the four-period QW. More interestingly, Fig. 1(f) shows that the number of gap-closed line segments with Re(E3)=0 is not equal to that with Re(E3)=π. Even the gap closes only with Re(E3)=πin Fig. 1(g), and closes only with Re(E3)=0 in Fig. 1(h). These three situations do not appear for the threeperiod QW.

Fig.1. The dispersion relation diagrams of the non-unitary three-period quantum walk(up pattern)and the four-period quantum walk(down pattern)for different values of(θ1,θ2): (a)(θ1,θ2)=(?4π/5,?3π/5),(b)(θ1,θ2)=(?π/10,π/8),(c)(θ1,θ2)=(π/4,π/4),(d)(θ1,θ2)=(4π/5,4π/5),(e)(θ1,θ2)=(?4π/5,?4π/5),(f)(θ1,θ2)=(?π/5,π/5),(g)(θ1,θ2)=(?3π/5,2π/5),(h)(θ1,θ2)=(?2π/5,2π/5).
In general, the band gap closes equally with both Re(Em) = 0 andπfor the odd-period QW, while for the even-period QW the number of gap-closed line segments with Re(Em)=0 andπmay be unequal. The reasons why the results obtained from the three-period QW and the four-period QW can be generalized to the universal odd-period QW and even-period QW are given in the following.For the odd-period QW, the time-evolution operator ?Umchanges the positions of the walker from odd (even) sites to even (odd) sites at every iteration. By changing the order of the basis to separate even and odd sites, ?Umis described as the anti-block diagonal form

It is found that ?Umsatisfies the relation


We can obtain the relationτm?Umτm= ?Um,which does not enforce the constraint on the relation of 0-energy states andπenergy states.
3.2. Characterizing topological phases
Because the time evolution operator is a non-unitary operator,we cannot calculate winding numbers in an ordinary way.We characterize topological phases using topological numbers given by the global Berry phase.[24]The global Berry phase?Bis defined as



Fig. 2. Phase diagrams of (aitary three-period quantum walk and (b) the non-unitary four-period quantum walk in coin parameter space(θ1,θ2)whenγ =0.1. Differenttopological phasesare characterizedby thewindingnumbers v′m in Fig.1(a)and(v′m,v′′m)in Fig.1(b). The colored symbols indicate the coin parameters for observing the topological edge states.


3.3. Topological edge states
To verify the bulk–edge correspondence of the QW with high topological numbers, we still use the inhomogeneous three-period and four-period QW as an example. We consider the QW to be on a lattice withNsites and a periodic boundary condition is used. Take


Eight isolated eigenvalues with Re(E3)=0 andπappear in Fig. 3(b). Figure 3(e) presents the corresponding eigenstates, two 0(π)-energy edge states appear at the boundaryx=0 and two others appear at the boundaryx=N/2, which illustrate that the number of 0-energy edge states equals that ofπ-energy edge states at each boundary for the odd-period QW as mentioned above. On the other hand, the winding numbers corresponding black circle dot and the blue circle dot in Fig. 2(a) are?1 and 3, respectively. The difference between them isδv′3=4. The total number of edge states at each boundary equalsδv′3,also satisfying the prediction of the bulk–edge correspondence.
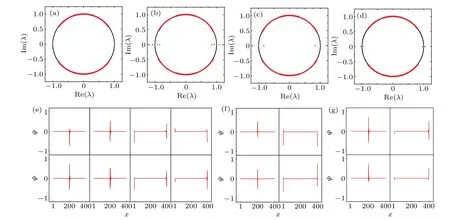
Fig. 3. The distributions of eigenvalue λ of the time-evolution operator U?3 are plotted in the complex plane for the case of (a)R=, (b)=, (c)=and (d)=. As a comparison, the black solid cycle represents an unit circle. Here,0-energy edge states(top pattern)and π-energy edge states(bottom pattern)are shown in(e),(f)and(g),which are the eigenstates corresponding to the isolated eigenvalues in(b),(c)and(d),respectively.

Fig.4. The distributions of eigenvalue of the time-evolution operator are plotted in the complexplane for thecasesof(a)Theeigenstatescorrespondingto the isolated eigenvalue on the real axes of(b),(c)and(d)are shown in(e),(f)and(g),respectively. The entire subfgiure(e),the top pattern of(f)and the top pattern of(g)show the 0-energy edge states,and the other patterns show the π-energy edge states.



4. Conclusion
In summary,we construct a one-dimensional multi-period non-unitary QW with PT symmetry. For simplicity and without losing generality, we take a non-unitary three-period QW and a four-period QW as examples to investigate the topological characteristics,and topological phases with large topological invariants are obtained. The results can be generalized to two types of multi-period QW, old-period QW and evenperiod QW. The values of the winding number can take±1,±3,...,±m(xù)for odd-period QW, and 0,±2,±4,...,±m(xù)for even-period QW under appropriate time frame,wheremis index of them-period QW. Depending on the choice of time frame, the maximum of high winding number can reach the number of shift operations in one-step evolution.
The distinction of two types of the multi-period QW is that the band gap closes equivalently at Re(Em) = 0 andπfor the odd-period QW, while the number of gap-closed line segments with Re(Em)=0 and that with Re(Em)=πmay be unequal for the even-period QW.The validity of the bulk–edge correspondence is numerically confirmed,the number of multiple edge states agrees well with the difference in topological numbers. It is worth noting that 0-energy edge states andπenergy edge states only coexist equally on the boundary for the odd-period quantum walk. However, for the even-period quantum walk,0-energy edge states andπ-energy edge states can exist unequally or even only one kind of edge states exist on the boundary. Our research has deepened the understanding of topology phenomena with large topological invariants in non-unitary or non-Hermitian systems.
- Chinese Physics B的其它文章
- Physical properties of relativistic electron beam during long-range propagation in space plasma environment?
- Heterogeneous traffic flow modeling with drivers’timid and aggressive characteristics?
- Optimized monogamy and polygamy inequalities for multipartite qubit entanglement?
- CO2 emission control in new CM car-following model with feedback control of the optimal estimation of velocity difference under V2X environment?
- Non-peripherally octaalkyl-substituted nickel phthalocyanines used as non-dopant hole transport materials in perovskite solar cells?
- Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study?

