馮亞芳,周廣良

(南京師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,江蘇 南京 210046)

1863年,Hermite首次研究了Z/pZ上的置換多項(xiàng)式,并且給出了一些判別置換多項(xiàng)式的方法. 其后Dickson將置換多項(xiàng)式的概念推廣到了任意的有限域中,并作了相關(guān)的研究. 在他的 《History of the Theory of Numbers》 一書(shū)中,整理了1922年之前的有關(guān)置換多項(xiàng)式的一些結(jié)果. 20世紀(jì)中期,Carlitz 等人做了一些新的研究,他們將Z/pZ上單變?cè)闹脫Q多項(xiàng)式推廣到了剩余類環(huán)以及一般環(huán)上的多變?cè)闹脫Q多項(xiàng)式. 近100年的時(shí)間里,置換多項(xiàng)式的一些結(jié)論已經(jīng)被廣泛地應(yīng)用于序列、密碼理論與密碼設(shè)計(jì)等領(lǐng)域,見(jiàn)文獻(xiàn)[1-4].

定義1記K=Fq,E=Fqn為有限域,對(duì)于任意的x∈E,我們定義x在K上的跡函數(shù)為TrE/K(x)=x+xq+xq2+…+xqn-1.當(dāng)q為素?cái)?shù)時(shí),我們把跡函數(shù)稱為絕對(duì)跡函數(shù),用Tr(x)來(lái)表示.

記K=Fq,E=Fqn跡函數(shù)有以下的幾條性質(zhì):

(1) 對(duì)于任意的α,β∈E,TrE/K(α+β)=Tr(α)+Tr(β).

(2) 對(duì)于任意的α∈E以及c∈K,TrE/K(cα)=cTr(α).

(3) 對(duì)于任意的α∈K,TrE/K(α)=nα.

(4) 對(duì)于任意的α∈E,TrE/K(αq)=Tr(α).

引理1[5]對(duì)于任意的b,c∈F2m,F2m上的二次多項(xiàng)式x2+bx+c=0 在F2m內(nèi)有解當(dāng)且僅當(dāng)Tr(b/a2)=0.

引理2設(shè)α,e均為正整數(shù),d=(α,e),那么當(dāng)e/d為奇數(shù)時(shí)(2α+1,2e-1)=1,當(dāng)e/d為偶數(shù)時(shí)(2α+1,2e-1)=2d+1.

以下為主要結(jié)果的證明.

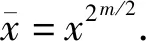
定理1設(shè)δ∈F2m,其中m是一個(gè)正偶數(shù),0≠a∈F2m/2且Tr(δ/a2)=1,那么

f(x)=(x2+ax+δ)2m/2-1+x2m/2+1

是F2m上的一個(gè)置換多項(xiàng)式.

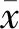
(1)

對(duì)(1)兩側(cè)提升2m/2次冪,得到:

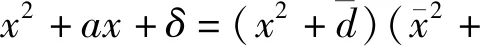
(2)

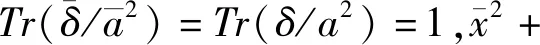
(3)

另一方面,由(2)可以得到

(4)

(3)與(4)兩側(cè)相減可得

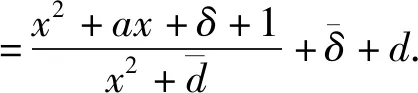
(5)

比較(3)(5)我們有

因此

簡(jiǎn)化可得

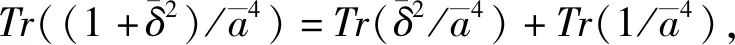
定理2設(shè)δ∈F2m且Tr(δ)=1,其中m≡0(mod 4),那么滿足(2m/2-2)k≡2m/2-1(mod 2m-1)的正整數(shù)k,f(x)=(x2+x+δ)k+x是F2m上的一個(gè)置換多項(xiàng)式.

證明首先,同余方程(2m/2-2)k≡2m/2-1(mod 2m-1)有解當(dāng)且僅當(dāng)(2m/2-2,2m-1)|2m/2-1.因?yàn)閙≡0(mod 4),所以2m-1為奇數(shù).因此(2m/2-2,2m-1)=(2m/2-1-1,2m-1)=2(m/2-1,m)-1.上述條件轉(zhuǎn)化成:2(m/2-1,m)-1|2m/2-1.也即(m/2-1,m)|m/2.由m≡0(mod 4)得m/2-1為奇數(shù),則(m/2-1,2)=1且(m/2-1,m/2)=1.于是(m/2-1,m)=1|m/2.即上述同余方程有解.要證明f(x)是置換多項(xiàng)式,我們只需要證明:對(duì)于任意的d∈F2m,方程

f(x)=(x2+x+δ)k+x=d

(6)

在F2m中有唯一的解.由于(2m/2-2)k≡2m/2-1(mod 2m-1),因此(6)化成

(x2+x+δ)2m/2-1=(x+d)2m/2-2.

(7)

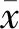
(8)

對(duì)方程(8)兩側(cè)都提升2m/2次冪得

(9)

把(8)和(9)的兩側(cè)相乘,我們得到

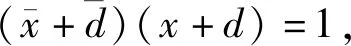
(10)

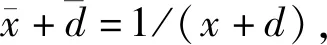
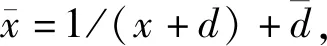
(11)

(8)和(11)相結(jié)合得到

因此

(12)

(11)與(12)比較,可得

簡(jiǎn)化得

令y=x+d,則

(13)

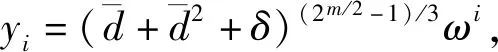
定理3設(shè)δ∈F2m且Tr(δ)=1,k|m,m/k是奇數(shù),那么對(duì)于任意滿足 (2k+1)k′≡1(mod 2m-1) 的正整數(shù)k′以及a∈F2k,均有f(x)=(ax2k+ax+δ)k′+x是F2m上的一個(gè)置換多項(xiàng)式.

證明當(dāng)a=0時(shí)顯然成立,下面假設(shè)a≠0.由于gcd(k,m)=k,并且m/k是奇數(shù),gcd(2k+1,2m-1)=1.那么x2k+1是F2m上的一個(gè)置換多項(xiàng)式.對(duì)于任意的d∈F2m,我們將證明f(x)=(ax2k+ax+δ)k′+x=d在F2m中有唯一的解.由于Tr(δ)=1,對(duì)于所有的x∈F2m,因此ax2k+ax+δ≠0.方程f(x)=d等價(jià)于

(ax2k+ax+δ)k′=x+d.

進(jìn)一步等價(jià)于

ax2k+ax+δ=(x+d)2k+1.

即

x2k+1+(d+a)x2k+(d2k+a)x+d2k+1+δ=0.

因?yàn)閍∈F2k,所以我們有a2k=a,即x2k+1+(d+a)x2k+(d+a)2kx+d2k+1+δ=0.公式等價(jià)于

x2k+1+(d+a)x2k+(d+a)2kx+(d+a)2k+1=δ+d2ka+a2kd+a2k+1.

即

(x+d+a)2k+1=δ+d2ka+a2kd+a2k+1.

由于x2k+1是F2m上的置換多項(xiàng)式,那么存在唯一的x∈F2m滿足上述方程.因此f(x)是F2m上的一個(gè)置換多項(xiàng)式.

定理4設(shè)δ∈F2m且Tr(δ)=1,如果m和k均為正偶數(shù)且m/gcd(k,m)是奇數(shù),那么對(duì)于任意滿足(2k+1)k′≡2m/2-1(mod 2m-1) 的正整數(shù)k′以及任意的a∈F2m/2,均有f(x)=1/(ax2k+ax+δ)k′+x是F2m上的一個(gè)置換多項(xiàng)式.

證明當(dāng)a=0時(shí)顯然成立,下面假設(shè)a≠0.由于m/gcd(k,m)是奇數(shù),gcd(2k+1,2m-1)=1.那么我們有x2k+1是F2m上的一個(gè)置換多項(xiàng)式.對(duì)于任意的d∈F2m,我們將證明f(x)=d在F2m中有唯一的解.由于Tr(δ)=1,對(duì)于所有的x∈F2xm,x2k+x+δ≠0.方程f(x)=d等價(jià)于 1/(ax2k+ax+δ)k′=x+d.

進(jìn)一步等價(jià)于

1/(ax2k+ax+δ)2m/2-1=(x+d)2k+1.

(14)

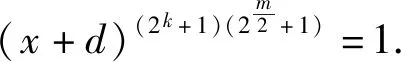
x2m/2=1/(x+d)+d2m/2.

(15)

由于x≠d,那么我們由方程(14)(15)可得

ax2k+ax+δ=(x+d)2k+1(ax2k+ax+δ)2m/2=(x+d)2k+1a2m/2((1/(x+d)+d2m/2)2k+(1/(x+d)+d2m/2)+(δ/a)2m/2)=

a2m/2(x+d+(x+d)2k+(x+d)2k+1((δ/a)2m/2+d2m/2+k+d2m/2))=a2m/2(x+d+x2k+

d2k+(x+d)2k+1((δ/a)2m/2+d2m/2+k+d2m/2)).

因?yàn)閍∈F2m/2,我們有a2m/2=a.化簡(jiǎn)上式可得

(x+d)2k+1=(δ+ad+ad2k)/(δ2m/2+a2m/2d2m/2+k+a2m/2d2m/2)=(δ+ad+ad2k)1-2m/2.

對(duì)于固定的δ,a和d,x2k+1是F2m上的一個(gè)置換多項(xiàng)式,那么方程(14)有唯一的解.這就證明了f(x)是一個(gè)置換多項(xiàng)式.

定理5設(shè)δ,a∈F2m,m,k,s均是正整數(shù),滿足gcd(m,k)>1,s(2k-1)≡0(mod 2m-1),那么f(x)=(ax2k+ax+δ)s+x是F2m上的一個(gè)置換多項(xiàng)式.

證明當(dāng)a=0時(shí)顯然成立,下面假設(shè)a≠0.多項(xiàng)式f(x)是一個(gè)置換多項(xiàng)式,當(dāng)且僅當(dāng)對(duì)于任意的d∈F2m,

(ax2k+ax+δ)s+x=d

(16)

在F2m中有唯一解.由方程(14)我們得到

(ax2k+ax+δ)j(2m-1)=(x+d)2k-1,

(17)

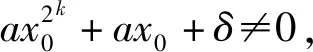
(a(d+α)2k+ad+α+δ)s+x=α.

(18)

由α2k+α=0,方程(18)簡(jiǎn)化成(d2k+d+δ)s+x=α,并且

x0=d+(d2k+d+δ)s=d.

(19)