Effective Hamiltonian of the Jaynes–Cummings model beyond rotating-wave approximation?
Yi-Fan Wang(王伊凡), Hong-Hao Yin(尹洪浩), Ming-Yue Yang(楊明月),An-Chun Ji(紀安春), and Qing Sun(孫青)
Department of Physics,Capital Normal University,Beijing 100048,China
Keywords: Jaynes–Cummings model,Floquet theory,high-frequency approximation
1. Introduction
The Jaynes–Cummings model (JCM)[1,2]provides a fundamental paradigm to capture many important phenomena[3–13]produced by the interaction between a twolevel (artificial) atom and a single-mode radiation field,e.g., the Rabi oscillations[3–7]and the entangled atom-field state.[8–10]Most of the previous works have focused in the regime of weak atom-light coupling, where the rotatingwave approximation(RWA)can be applied by neglecting the counter-rotating terms(CRTs). Nevertheless,such CRTs may become significant with the coupling strength, especially in the strong coupling regime which has been achieved in diverse systems,[14–22]and can give rise to new physics beyond RWA.[23–30]In these cases,appropriate treatment of the CRTs would be necessary.
Generally speaking, the energy spectrum of the JCM without RWA (or the Rabi model[31,32]) can be solved[33–35]with the help of numerical solutions.[36–40]However,it is not easy to analyze the physical properties of the model based on the numerical results. To gain the underlying physics in the presence of CRTs,various analytical approaches under different situations have been developed,[41–53]e.g.,the generalized RWA[42]and variational methods.[44–48]Nevertheless, a general treatment of the CRTs is still desirable.
In this paper, we revisit the JCM to go beyond the RWA from a new perspective. This relies on the important observation that the CRTs can be viewed as a kind of periodical process in a transformed basis, and thus enables a general treatment within the Floquet theory,[54–59]which has been widely and successfully used to engineer nontrivial Hamiltonians in periodic driving systems recently.[60–67]Different from the previous treatments, the CRTs in the extended Floquet space would mix the neighboring Floquet modes, and give rise to unique features. We find that the full energy spectrum of the original JCM can be extracted from the numerical simulations in the extended Floquet space,and the energy spectrum is folded in each quasi-energy band due to the equivalence among different bands. In the high-frequency regime,we derive an effective Hamiltonian with an enlargedU(1)symmetry, very different from theZ2symmetry of the original JCM.Specifically,the effects of CRTs are incorporated in a unique photon-number dependent atom-light detuning and coupling strength. Moreover,by further analyzing the energy spectrum, eigenstate fidelity and mean photon number of the resultant polaritons, we find that the high-frequency effective model can be applied up to an ultra-strong coupling regime,where the coupling strength is comparable with the frequency of the photon and is not significantly affected by finite atomlight detuning.
The paper is outlined as follows. In Section 2,we present the model and derive the high-frequency effective Hamiltonian in the Floquet theory. In Section 3,we analyze the energy spectrum,the eigenstate fidelity and the mean photon number of the polaritons of the effective model,which are compared to the full numerical simulations in the extended Floquet space.The influence of a finite atom-light detuning is also discussed.Finally,we give a brief summary in Section 4.
2. Model and formalism
We begin with the Jaynes–Cummings model in the presence of CRTs(or the Rabi model). In the Schr¨odinger picture,the total Hamiltonian of the system can be written as (we set=1 throughout the paper)
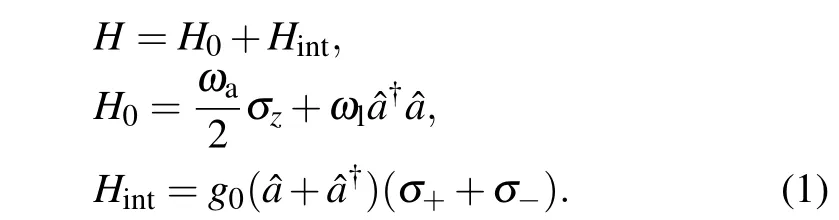

withδ=ωa?ωlbeing the atom-light detuning. We can realize that in this rotating frame, the CRTs exhibit timedependent exponential factors, which just play as periodic drives with frequencyω ≡2ωl.
In the Floquet theory, the (slow) evolution in a cycle of the above periodically driven system can be described by an effective time-independent(Floquet)HamiltonianHFeff.We are interested in the high-frequency regime whereωis the largest energy scale so that we can expandHFeffas

withV(1)=(V(?1))?=g0?σ+and=?.I2is 2×2 unit matrix. One can see thatH(1)introduces a photon-numberdependent detuning(the dynamical Stark shift)from the twophoton process. While for the second order 1/ω2,we can derive(see Appendix A for detail)
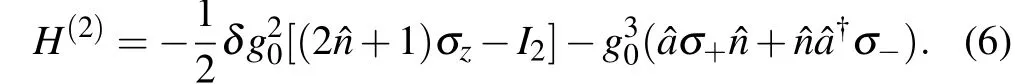
Here the terms in the first bracket describe the contribution of a finite atom-light detuning away from resonance (δ=0).The second bracket gives a correction to the atom-light coupling with a photon-number-dependent coupling strength from the three-photon process. It is interesting to see that even though the CRTs mix subspaces with different excitation numbersNex≡?+σ+σ?, the effective Hamiltonian conserves the total excitations,i.e.,[Nex,HFeff]=0. With thisU(1)symmetry,the effective Hamiltonian(3)has the same integrability with the JCM under RWA,in contrast to theZ2symmetry held by the original Hamiltonian (1), and thus can be solved analytically as shown in the following section.
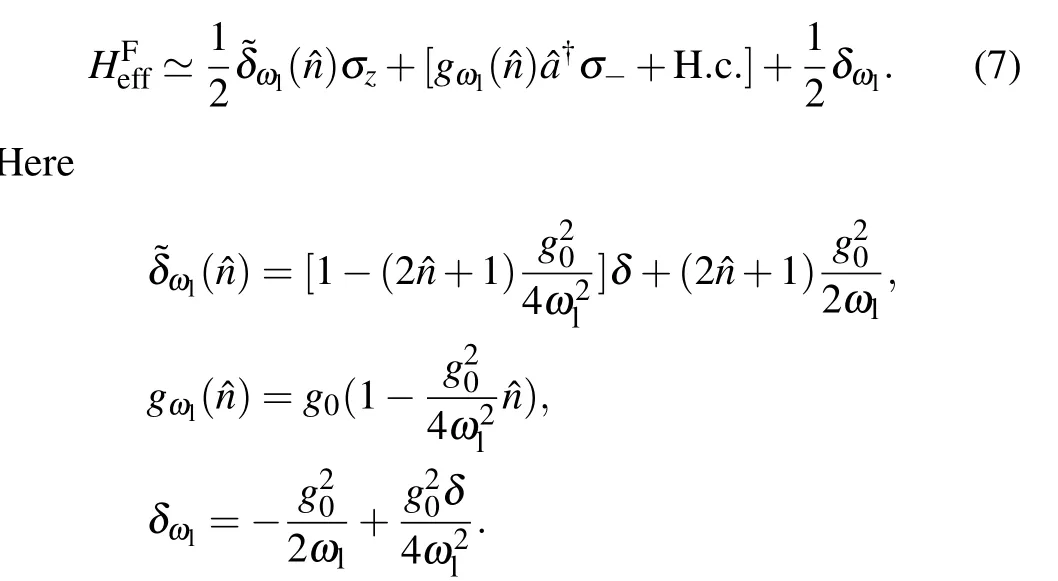
Now,we arrive at a high-frequency effective Hamiltonian given by One can see that compared to the JCM with RWA, both the effective detuningωl() and atom-light couplinggωl() are renormalized by the CRTs and depend on the photon numberas well as the light frequencyωl.
Equation (7) is the main result and the starting point of this paper, and we will see in the following that the nontrivial contributions brought by the CRTs on the energy and mean photon number of the JCM can be well captured in the effective model with high eigenstate fidelity up to the regime with ultra-strong coupling strength.
3. Results and discussion
Before going into details of the effective model, we first discuss the typical features of the quasi-energy bands of the JCM in the extended Floquet space. As shown in Fig.1, one can see that the quasi-energy in neighboring bands is separated by 2ωlas expected. Forg0/ωl?1,all energy branches in different bands are well separated, where the RWA can be applied. With the increasingg0/ωl, the energy branches of large excitation(photon)number in neighboring bands first get touched(energy gap closing)and then those of relative smaller excitations. Untilg0/ωl?1, all branches in different bands are involved. Forg0/ωl?1, most of the low-excitation energy branches are well isolated in each band,implying that the effect of CRTs can be included in the effective model to be shown in the following.
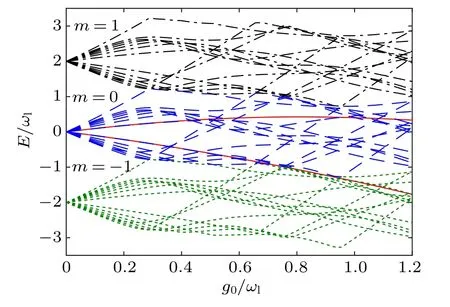
Fig. 1. The quasi-energy as a function of g0/ωl for m=?1 (green dotted),m=0(blue dashed)and m=1(black dash-dotted)band in the extended Floquet space for δ=0.The two energy branches of the effective model for excitation number Nex=1 are also plotted for illustration(red solid).
We now discuss the energy spectrum of the effective Hamiltonian (7). As the total excitation numberNexis conserved,Eq.(7)can be solved in the subspace spanned by two product states|g〉?|Nex〉and|e〉?|Nex?1〉for eachNex,
where|g〉(|e〉) denote the atomic ground (excited) state, and|Nex〉(|Nex?1〉)is the photon Fock state with photon numberNex(Nex?1). In this basis,Hamiltonian(7)is block diagonalized with each block taking the form of
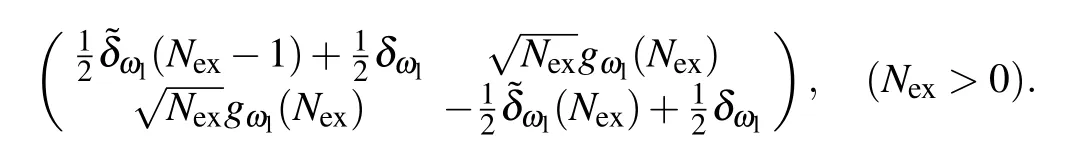
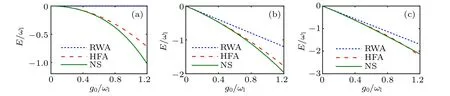
Fig.2. The lower-branch energy E?/ωl as a function of g0/ωl of the HFA(red dashed)for excitation number Nex =0(a),1(b),and 2(c)at resonance δ =0. The corresponding energy branches under RWA(blue dotted)and by numerical simulations(NS,green solid)are also plotted for comparison.
After a straightforward diagonalization, we can obtain two energy branches of the polariton for eachNex,
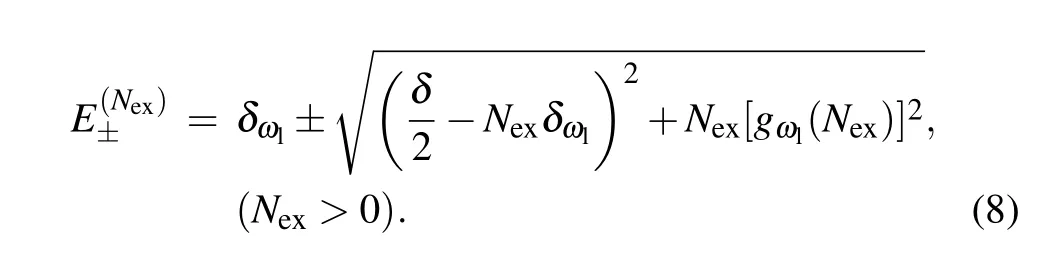
Notice thatNex=0 gives the ground state with energyEg=?δ/2+δωl.
In Fig.2,we plot the lower energy branchE?as a function of coupling strengthg0at resonanceδ= 0 for the interested low excitation numbersNex. For comparison, we have also presented the results from RWA and a full numerical simulation beyond high-frequency approximation (HFA)in the extended Floquet space(see Appendix B for detail). We can see that the RWA is mainly justified forg0/ωl?1, and the deviations from the numerical results become remarkable with the increasing atom-light coupling strengthg0,indicating the breakdown of RWA in a strong coupling regime. On the other hand, the effective Hamiltonian gives a quite good approximation forg0/ωl?0.6 and works qualitatively well up tog0/ωl≈1. The validity of the HFA in this regime resides in the well separation of quasi-energy bands for not too largeg0.While forg0/ωl?1,the different Floquet bands get involved and the HFA is no longer applicable.

Fig.3. The lower-branch energy E?/ωl as a function of atom-light detuning δ/ωl under RWA(blue dotted),HFA(red dashed)and NS(green solid)for coupling strength g0/ωl=0.2[(a),(d)],0.3[(b),(e)],and 0.4[(c),(f)]. Here,the excitation number is Nex=0 for(a)–(c)and Nex=1 for(d)–(f),respectively.


with
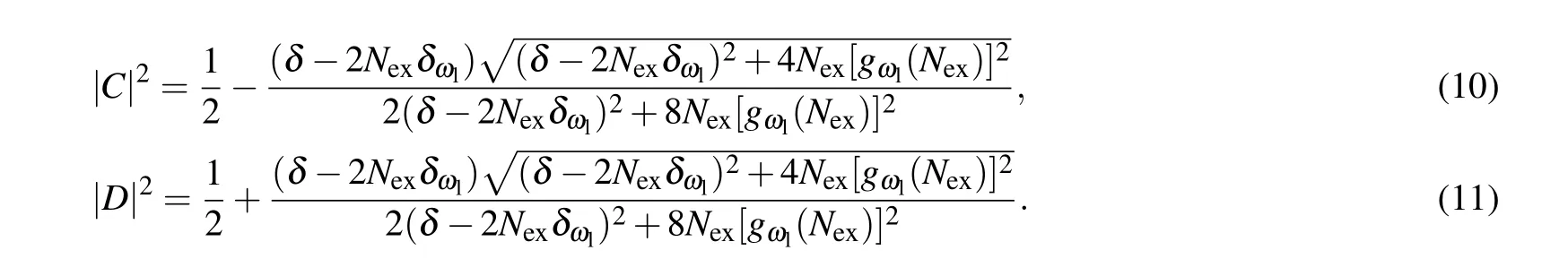
HereCandDare the complex amplitudes in the dressed excited and ground state respectively satisfying|C|2+|D|2=1.We introduce the time-averaged fidelityin a cycle between the eigenstate of the effective model|ψ〉Nexand the Floquet eigenstate|ψ(t)〉(see Appendix B),which is defined by
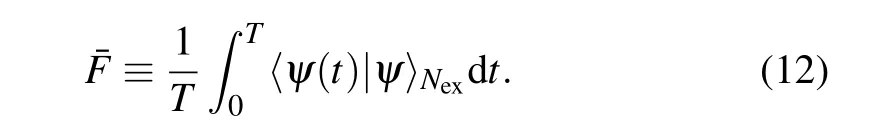
In Fig.4,we give the fidelity distribution in theg0–δplane for the lower branch ofNex=1. We find≥0.9 in a broad parameter regime, suggesting that the effective model is a quite good approximation of the JCM.
Fig.4.The time-averaged fidelity between the eigenstate of the effective model and the Floquet eigen-mode in the g0–δ plane for the lower branch with Nex=1. The red dashed line labels =0.9.
So far, we have discussed the polariton energy spectrum and the eigenstate fidelity of the effective model. It is also worthy to obtain the mean photon number of the polariton,which can be measured in experiment. Taking use of the explicit form of the eigenstate, the mean photon number of the lower branch is given by
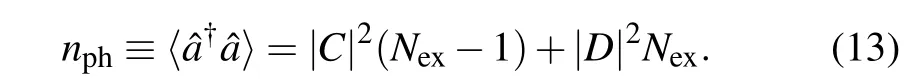
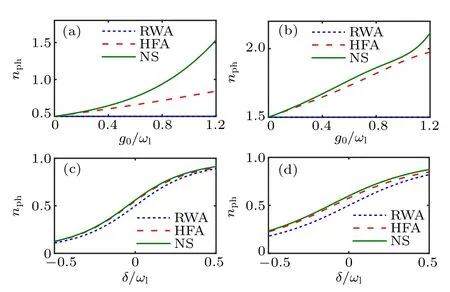
Fig.5.The mean photon number nph of the lower branch as functions of g0/ωl [(a),(b)]and δ/ωl [(c),(d)]under RWA(blue dotted),HFA(red dashed) and NS (green solid). Other parameters are: [(a), (b)] δ =0,Nex=1 and 2;[(c),(d)]Nex=1,g0/ωl=0.2 and 0.3.
In Figs. 5(a) and 5(b), we plot the mean photon numbernphas a function of coupling strengthg0at resonance for the lower branch of excitation numberNex=1 and 2. Different from the RWA which gives a coupling-independent constant value,the mean photon number in the lower branch of the effective model increases with the coupling strength, in accordance with the numerical results,due to the fact that the contributions from states with higher excitation numbers brought by CRTs become significant, which are incorporated in the photon-dependent coupling strength and detuning in the effective Hamiltonian (7). Figures 5(c) and 5(d) show the dependence of mean photon numbernphon the detuningδ. Similar to the energy discussed above, the mean photon number predicted by the effective model agrees quite well with the numerical simulation even for large detuning|δ|?0. Specific forδ ?0,the component~|e〉?|Nex?1〉in the wave function is dominated andnph→0. While forδ ?0,the atom is mainly in the ground state with a nearly free photon,|g〉?|Nex〉,giving rise tonph→1.
4. Conclusion
We have studied the JCM in the frame of Floquet theory.By treating the CRTs as periodic drives, we solve the model in the extended Floquet space and derive an effective Hamiltonian with enlargedU(1) symmetry in the regime of high“driving”frequency. We find that the energy spectrum as well as the mean photon number predicted by the effective model agrees well with the numerical simulations of high eigenstate fidelity in a broad parameter regime even for an ultra-strong atom-light coupling,where the coupling strength is comparable with the photon frequency and the RWA generally breaks down. The Floquet method developed in this work provides a systematic and efficient way to study the nontrivial physics brought by CRTs,and can also be applied to other situations,e.g.,the multimode atom-cavity systems,coupled atom-cavity arrays and dispersive atom-light couplings.
Appendix A:Derivation of the effective Hamiltonian
In this paper, the rotational Hamiltonian(2)can be written as

Appendix B: Numerical simulation in the extended Floquet space
B1. The matrix of the quasi-energy operator
In the extended Floquet space, the basis states for the HamiltonianH'can be written as|αm(t)〉={|e,n〉eimωt,|g,n〉eimωt}, wheren ∈N is the photon number andm ∈Z is the‘photon’index. The time-periodic-averaged matrix of the quasi-energy operatorG=H'?idtcan be written as[56]

As the parity of the excitation number in the HamiltonianH'is conserved (even or odd), we can diagonalize the above Hamiltonian in each subspace with fixed parity. Numerically,we have truncated the infinite matrix by choosingnmax=21,mmax=10 for odd space andnmax=20,mmax=10 for even space.
B2. Mean photon number
After diagonalizing the matrix (B1), we can obtain the eigenenergy (quasi-energy)εjand the corresponding eigenstate


- Chinese Physics B的其它文章
- Coarse-grained simulations on interactions between spectrins and phase-separated lipid bilayers?
- Constraints on the kinetic energy of type-Ic supernova explosion from young PSR J1906+0746 in a double neutron star candidate?
- Computational model investigating the effect of magnetic field on neural–astrocyte microcircuit?
- Gas sensor using gold doped copper oxide nanostructured thin films as modified cladding fiber
- Exact explicit solitary wave and periodic wave solutions and their dynamical behaviors for the Schamel–Korteweg–de Vries equation?
- Suppression of ferroresonance using passive memristor emulator

