Computational model investigating the effect of magnetic field on neural–astrocyte microcircuit?
Li-Cong Li(李利聰) Jin Zhou(周瑾) Hong-Ji Sun(孫洪吉) Peng Xiong(熊鵬)Hong-Rui Wang(王洪瑞) Xiu-Ling Liu(劉秀玲) and Chang-Yong Wang(王常勇)
1College of Physics Science and Technology,Hebei University,Baoding 071002,China
2Key Laboratory of Digital Medical Engineering of Hebei Province,Hebei University,Baoding 071002,China
3Department of Neural Engineering and Biological Interdisciplinary Studies,Institute of Military Cognition and Brain Sciences,Academy of Military Medical Sciences,Beijing 100850,China
4Brainnetome Center,Institute of Automation,Chinese Academy of Sciences,Beijing 100190,China
Keywords: magnetic stimulation, neural–astrocyte microcircuit, excitatory and inhibitory balance, computational model
1. Introduction
Extremely low-frequency magnetic field (ELF-MF,<300 Hz)therapy has proven to be a promising therapeutic tool in both physical and mental diseases.Specifically,transcranial magnetic stimulation(TMS)can modify the excitability of the brain in a painless and non-invasive fashion through the placement of a coil above the skull over regions of interest. Based on the high biological effectiveness,TMS is widely employed in both clinical applications and basic research related to depression,[1]epilepsy,[2]Alzheimer’s disease,[3]and Parkinson’s disease.[4]Nevertheless, numerous studies of magnetic stimulation (MS) conductedin vitroandin vivoshow that the stimulation parameters vary significantly among studies;therefore,it is difficult to interpret the results of certain treatments in the clinical setting.[5]The reasons for this variability remain unclear but several factors likely contribute, one of which is the interindividual and anatomical variability.[6–8]The surface of the brain is highly folded and the different neuronal populations vary considerably with respect to the orientation of MS-induced intracranial electrical fields,[9]which complicate the coil positioning and activation site.[10]Additional consideration is primarily due to the fact that the effects of MS on cellular function and cell–cell interactions are not completely clear.
To provide a better understanding of the mechanism underlying MS-based therapies,several studies have investigated MS-cell interactions. The results suggest that modification of synaptic plasticity, ion channels, resting membrane potential,and action potential threshold may be the potential mechanism for TMS.[11,12]New tools have been designed to study the influence of TMS on neurons in the brain.[13,14]In addition to these experimental studies, there exists a wealth of published computational models to investigate the mechanism underlying MS.These models overcome the limitations of single-scale research and strong electrical artifact,and can directly record the neuronal membrane potential during MS.[15–18]In particular,some studies explore the influence of a magnetic field on neuronal morphology and screen the related sensitive parameters of neurons.[19]Taken together,these data indicate that MS has a direct effect on neuronal excitability; nevertheless, it is challenging to integrate these experimental and computational results into a unified framework in terms of putative physiological mechanisms.This may be due to the fact that MS studies concentrate heavily on modeling neuronal functions and largely overlook the potential influence on non-neuronal cells,including one type of glial cell: astrocytes.
Indeed,neurons are surrounded by astrocytes,leading to the “tripartite synapse (TpS)” model consisting of pre- and post-synaptic neurons and astrocytic processes.[20]Accordingly,the tight morphological arrangement renders astrocytes likely cellular effectors of TMS.Recent advances have demonstrated that the viability and morphological properties of astrocytes are not affected during MS treatment under different parameters,while the concentration of calcium in astrocytes significantly increases.[21–23]These experimental findings have also been observed during deep brain stimulation (DBS) and transcranial direct current stimulation (tDCS).[24,25]In cultured astrocytes and hippocampal slices,intracellular calcium(Ca2+) elevation causes the release of multiple gliotransmitters such as glutamate,ATP,and GABA,which have the ability to send signals to neighboring neurons and regulate neuronal activity and synaptic behavior(for reviews,see Refs.[26–28])The change in Ca2+dynamics shows the ability of astrocytes to respond to electromagnetic activity directly or indirectly,suggesting a potential role for astrocytes in mediating the therapeutic effect of MS on synaptic efficacy. However,no study has completely described the impact of MS on astrocytes and neurons,leaving some important questions unanswered. How do astrocytes respond to MS at different frequencies? What are the effects of astrocytes on excitatory neurons during MS?What are the key factors of magnetic field regulation on neurons and astrocytes?
Here,we attempted to address these issues by devising a biophysical computational model to investigate the effects of MS on neuron–astrocyte interactions. The employed model architecture is based on the physiological and anatomical features of the CA subfield of pyramidal cell-interneuron circuit in the hippocampus,[29]which is one of the main targets of TMS. In contrast to previous models, which either focused on constructing large scale models of the neuronal network or modeling the effects of TMS on simple pyramidal cells with arbitrary morphology, we focused on neurons and astrocytes as the cellular targets of MS with a view to providing a realistic explanation under actual biological conditions. Numerical results show that the neuronal magnetic threshold and synaptic coupling strength profoundly affect the effects of MS.Under different parameters,MS can induce an astrocyte response,thereby dynamically modulating neuronal excitability to maintain the neuronal excitatory–inhibitory balance. Our study developed the first computational model that offers new clues to understanding the physiology of MS by demonstrating the biophysics acting on neural–astrocyte microcircuits in the hippocampus.
2. Methods
In the present study, we used a modified version of the neural–astrocytic microcircuit model initially developed by Nardkarni and Jung to describe the interaction between neuronal and astrocytic activity.[30]The model comprises a pyramidal cell,an interneuron,and an astrocyte,as shown in Fig.1.The interneuron is connected to the pyramidal cell through a GABAareceptor-mediated inhibitory postsynaptic current(IPSC) and the pyramidal cell is connected to the interneuron through NMDA and AMPA receptor-mediated excitatory postsynaptic currents (EPSC). Depending on the location of the astrocyte, we added slow inward currents (SICs) induced by the astrocyte to regulate the interneuron and pyramidal neuron. Subsequent sections describe the mathematical formulas in detail.
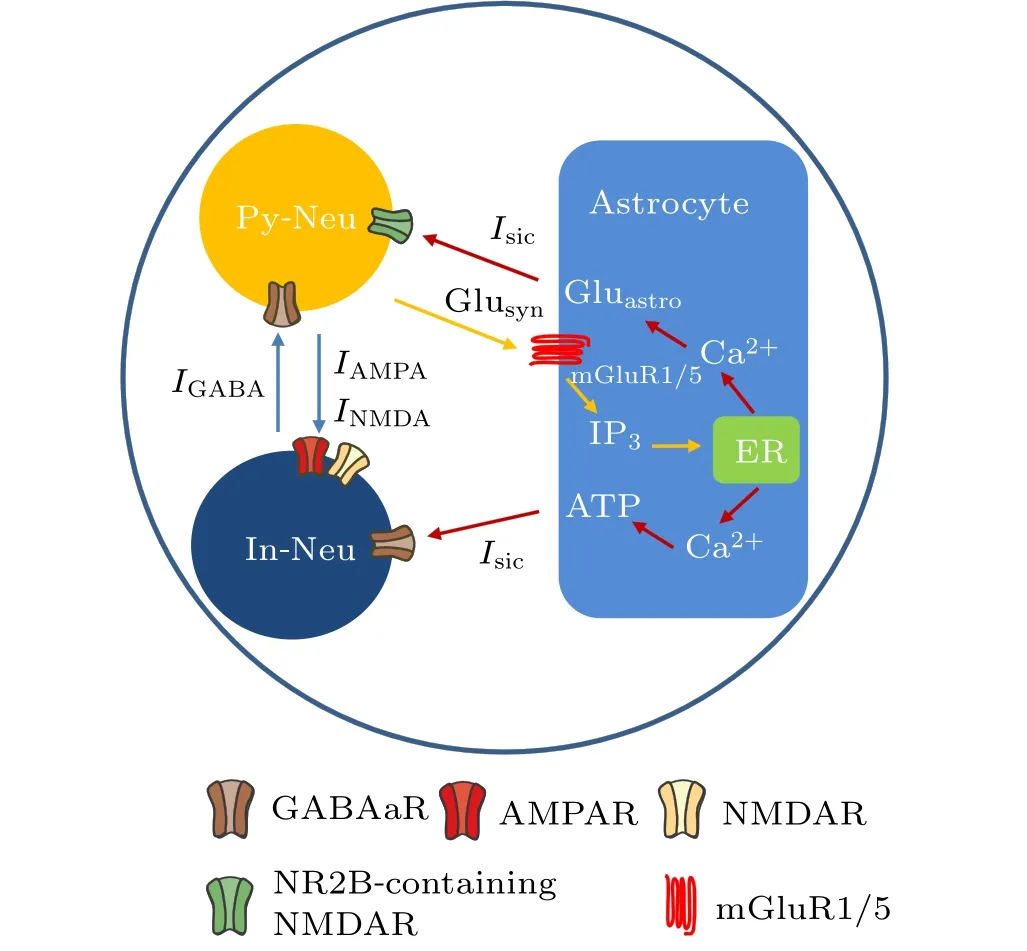
Fig.1. The main pathways of magnetic field action on the tripartite synapse model. Py-Neu and In-Neu represent pyramidal neuron and interneuron,respectively. Inhibitory synaptic current (IGABA) and excitatory synaptic currents (INMDA and IAMPA) are mediated by the corresponding receptors GABAaR, NMDAR, and AMPAR. Glusyn and Gluastro represent glutamate released from presynaptic terminal and astrocyte, respectively. ER refers to the endoplasmic reticulum. The blue, orange, and red arrows represent synaptic currents, astrocyte activation, and astrocyte regulatory pathways to neurons, respectively. Noteworthy, the locations of astrocytic and neuronal receptors in this figure do not represent their exact physiological distribution.
2.1. Excitatory pyramidal neuronal model
Previous modeling and experimental studies have demonstrated that the initial segment of MS may be different, occurring within the soma,descending axon,or both.[9,31]Thus,the minimum individual neuronal unit used to investigate the effects of a magnetic field has at least two spatially separated compartments. In the present study, we used the twocompartment Pinsky–Rinzel model (P–R) for hippocampal pyramidal cells,[32]which consists of a dendritic and a somatic compartment, as shown in Fig.2. The model is described by the following current-balance equations:

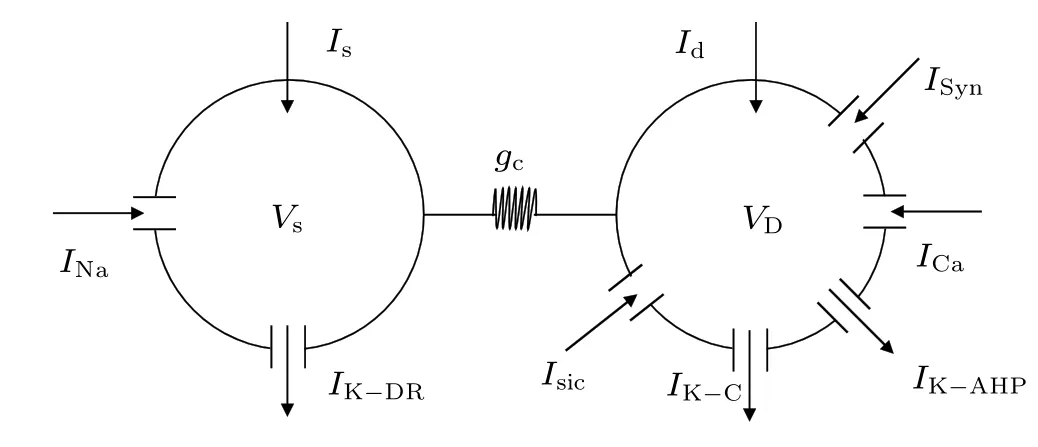
Fig. 2. Schematic diagram of a two-compartment model for a single P–R neuron.
The parameters used in the pyramided neuron model are listed in Table 1.
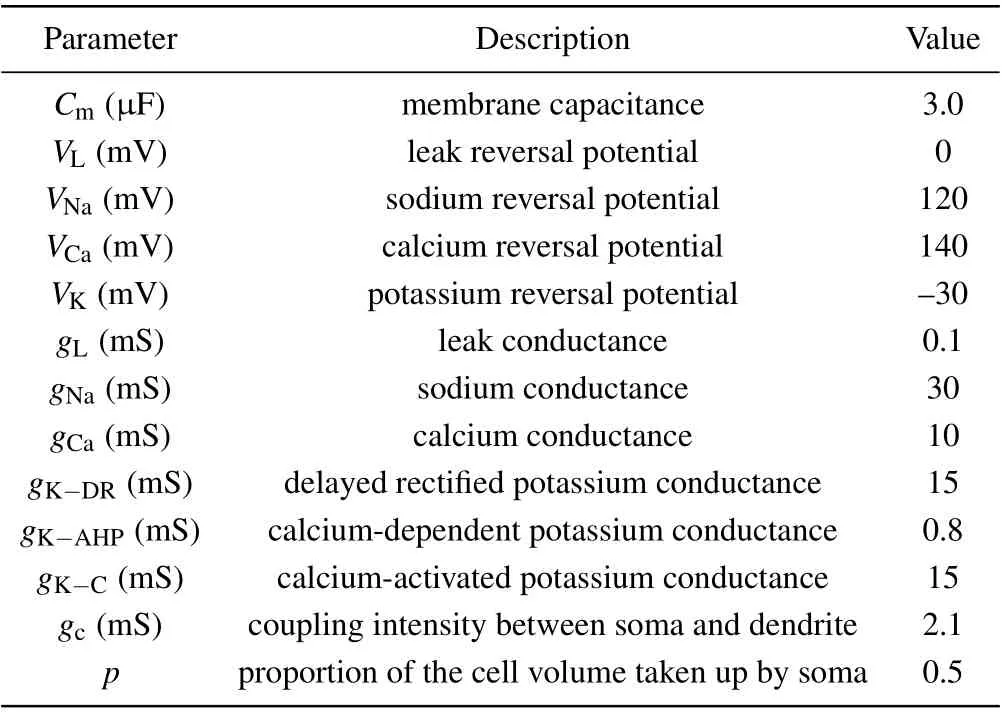
Table 1. Parameters used in the pyramidal neuron model.[32]
2.2. Inhibitory interneuronal model
Interneurons are commonly thought of as local circuit neurons and exist as diverse types.[33]In this study, the interneuron is described by a single compartment model developed by Wang and Buzsaki,[34]whose kinetics and maximal conductance fit to hippocampal fast spiking interneurons. The dynamic equations are given below:

The parameters used in the interneuronal model are given in Table 2.
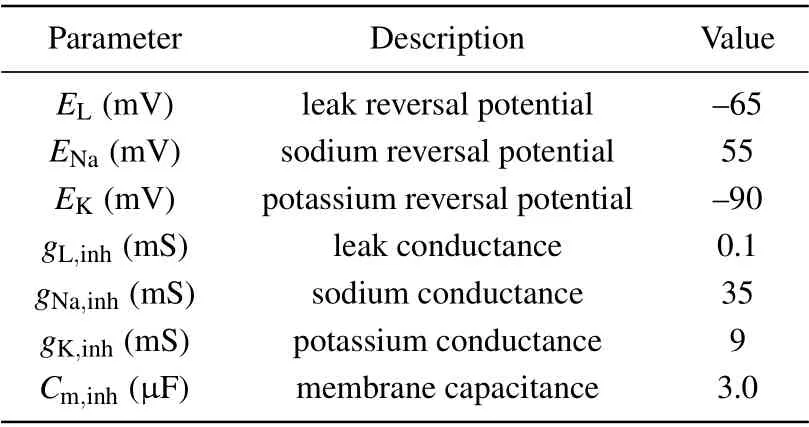
Table 2. Parameters used in the interneuronal model.[34]
2.3. Magnetic field model
According to Faraday’s law, the time-varying magnetic field(MF)B(t)applied to the brain can induce a time-varying electric field(EF)E(t),which may result in small changes in the membrane potential of neurons,thereby producing biological effects.
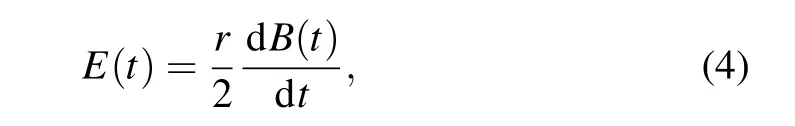
whereris the radius of exposure. The induced EF exerts alternating forces on free ions,F=E(t)zqesinωt(z, the ion’s valence;qe=1.6×10?19C,the electron’s charge;ω=2π f,circular frequency).[35]In this way, the oscillating ions may be able to disrupt the membrane’s electrochemical balance,altering membrane potential. Numerous electrophysiological studies show that field-induced membrane depolarization ?vis induced by EF.[36]
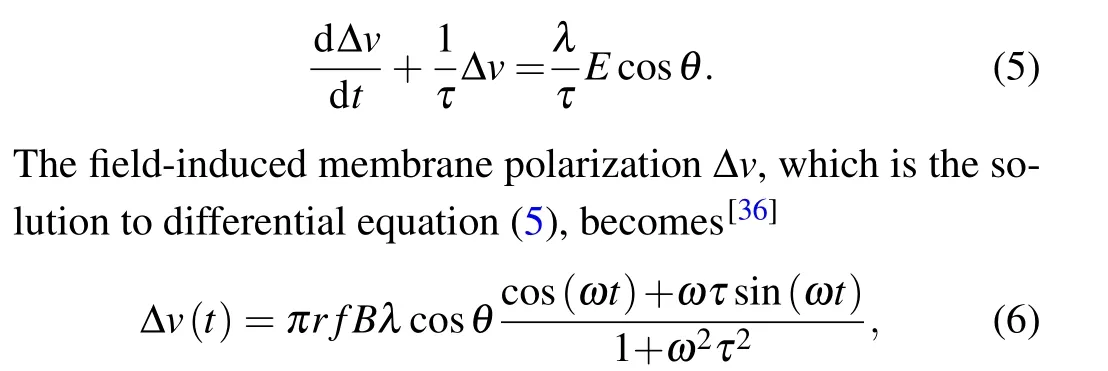
whereλdenotes the polarization length 0.5 mm,τis the Maxwell–Wagner time constant 10?4s,Bis the intensity amplitude of MF,andris the radius of exposure with 10 cm.θis the angle between the axis of the EF and the neurons. Given that the size of the neurons is much smaller than the range of magnetic field, to simplify, our model hypothesized that MF and its induced EF were uniformly distributed throughout the neuron, and the neurons are completely affected by the electric field,i.e.,cosθ=1. Subsequently,the perturbation ?vof the membrane potential was integrated into the models of neuronal dynamics described above in Eqs.(1)–(3). Based on the function of TimedArray in Brian2 simulator,[37]pulse width of magnetic field was modeled with 10-ms duration.[38]Thus,we can calculate the field-induced perturbation of neuronal membrane potential at any time under pulse MF as shown in Fig.3.
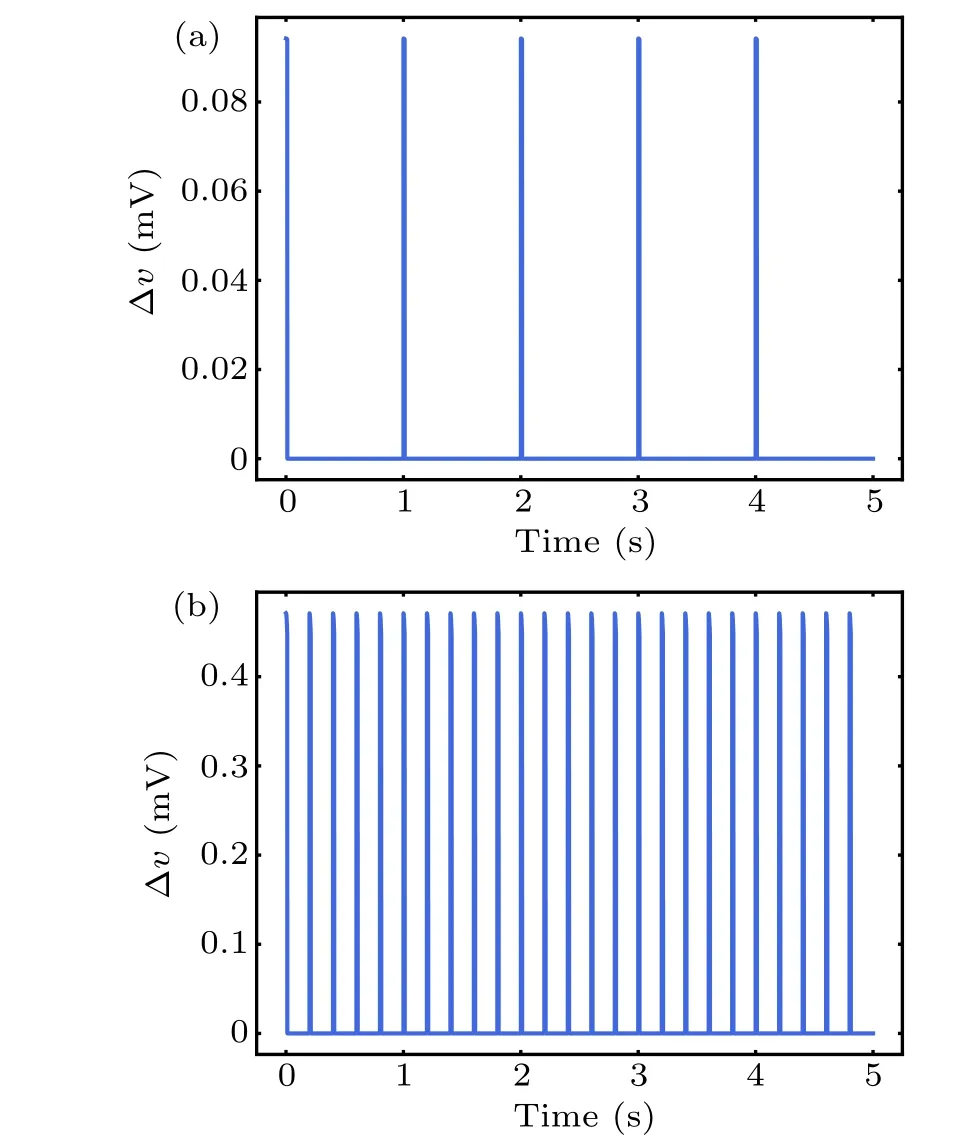
Fig. 3. Perturbation ?v of neuron membrane potential by series of pulsed magnetic field with 1 Hz(a)and 5 Hz(b).
2.4. Synaptic currents model
In most biophysical computational models, neurons are connected by chemical synapses, which are activated by action potentials triggered by presynaptic neurons. Upon the arrival of an action potential at the presynaptic terminal, neurotransmitters are released into the synaptic cleft. Here, the phenomenological model originally introduced by Tsodyks–Markram.[39]was used to describe the amount of released glutamate or GABArsat timetk, which can be read by the following set of equations:
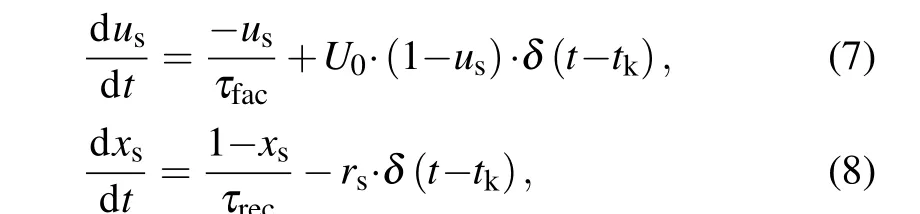
whereusis the available neurotransmitter resources“docked”for release and decay to zero at a rate of 1/τfac;xsrepresents the fraction of total neurotransmitter available for release and recovery to one at rate of 1/τrec.The equations for the released fraction of neurotransmitters read

wheregcis the clearance rate of the neurotransmitter;ρeis the vesicular to mixing volume ratio;andYTrepresents the total vesicular neurotransmitter concentration in the presynaptic boutons.
Glutamate and GABA in the synaptic cleft bind postsynaptically to corresponding receptors, giving rise to synaptic currents. The kinetics of the fast-type glutamate and GABA receptors can be represented by the following two-state diagram:[41]

whereCandOrepresent the unbound and bound states of the channel to neurotransmitter, respectively;Tis the glutamate or GABA concentrationGs;andαandβare the forward and backward rate constants, respectively. The fraction of receptors in the open stateris described by the following first-order dynamic equation:
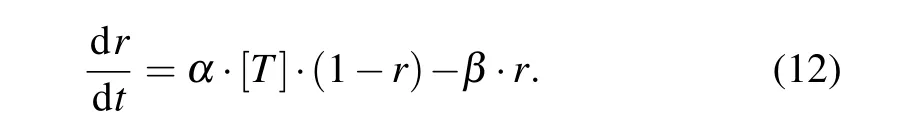
Then, NMDA-, AMPA-, and GABAa-mediated postsynaptic currents are expressed as functions ofr(t)and the membrane potentialvby the following equations:[41]

2.5. Astrocytic model
In contrast to the membrane model for neurons, the astrocytic model is nonelectrical and cannot generate action potentials. The excitability of astrocytes is represented by transient and repetitive elevations in intracellular calcium concentration.A plethora of examples of strategies for modeling gliotransmission or astrocyte–neuron interaction depend on astrocytic Ca2+levels.[43]In our model,the calcium oscillations are subjected to synaptically released glutamate and external stimulation by an MF.At the cellular level,the main processes underlying the signaling pathways of neuron–astrocyte interplay involve multiple successive events,as shown in Fig.1. Glutamate is released from presynaptic terminals of glutamatergic neurons and binds to types 1 and 5 metabotropic glutamate receptors on the astrocytic membrane. The activation of astrocytes triggers the production of the second messenger inositol 1,4,5-trisphosphate(IP3),which modulates the intracellular concentration of calcium ions. Subsequently, an elevation in IP3concentration induces the release of Ca2+from the endoplasmic reticulum(ER)to the astrocytic cytosol,thereby triggering Ca2+-dependent gliotransmitters release into the extracellular space,which in turn influences the dynamics of the neurons. The production of intracellular IP3is modeled by[44]
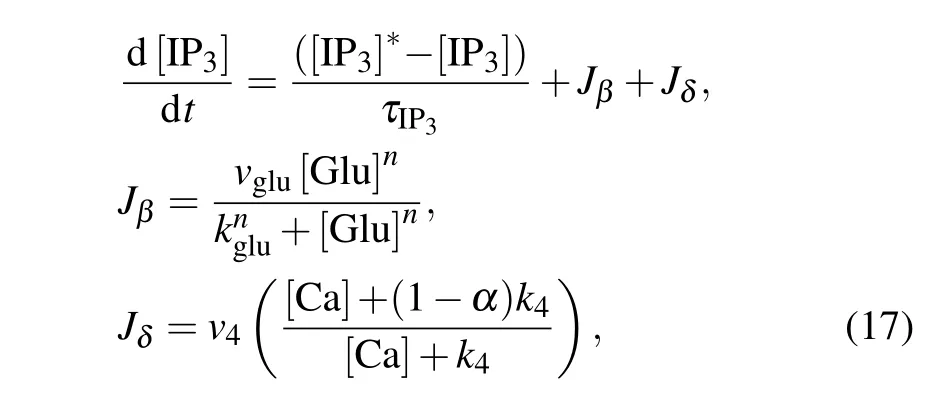
where the first equation describes IP3degradation and enforces a steady state at a degradation rateτIP3=7 s and an equilibrium concentration[IP3]?=0.16μM.The second and third equations describe IP3production by phosphoinositidespecific phospholipase C(PLC-β)and Ca2+-activated PLC-δ.The effective rate of IP3production depends on the amount of glutamate in the synaptic cleft[Glu].
A peculiar feature of intracellular Ca2+dynamics in astrocytes is its coupling with IP3receptor channels.Experimental results have clearly demonstrated that calcium is released from intracellular stores after exposure to an MF.[21]We used the Li–Rinzel model to describe Ca2+exchange and release in astrocytes.[45]This process contains three fluxes across the ER membrane: Ca2+flux release from the ER through the IP3Rgated ion channelsJchannel, Ca2+uptake from the cytosol to the ER by ATP-dependent pumpJpump, and Ca2+leak from the ERJleak. The astrocyte calcium model is described by the following equations:
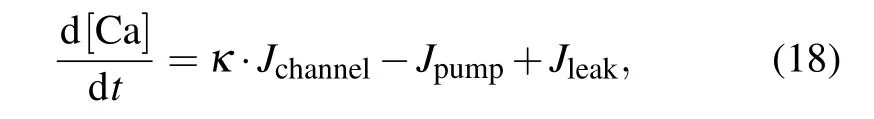
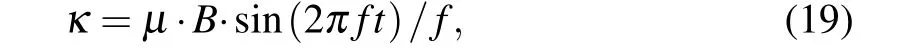
where we introduce the coupling coefficientκto describe the effects of an MF on the IP3R-gated Ca2+channels in the ER andμis the Ca2+permeability in the range of 3.5 μM·s?1.For the sake of simplicity, the expansions and parameters of terms are described in supplementary materials.
When the Ca2+concentration exceeds a certain thresholdCθ, gliotransmitters are released extra-synaptically via vesicular exocytosis. Astrocytes alter the state of the nearby synapses and affect neuronal excitability by injecting slow inward currents.[46]Nadkarni and Jung fit their experimental data using the following current function to model the effect of the astrocytic Ca2+concentration on neuron excitability:[47]
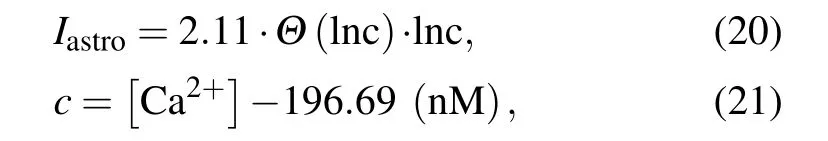
whereΘis the Heaviside function. In the present study,astrocytes fail to feed currentsIastroback to the neurons when the Ca2+concentration is less thanCθ.
Numerous physiological studies have shown that a single astrocyte can decode neuronal activity,[48]and release distinct gliotransmitters,[49]such as glutamate and ATP. ATP released from astrocytes can directly activate hippocampal interneurons,[50,51]whereas astrocyte-derived glutamate can enhance pyramidal neuronal excitability.[52,53]These findings indicate that astrocytes have the ability to differentially regulate neurons:


3. Results
Based on the components mentioned above, we simulated the neural–astrocyte microcircuit computational model.The entire model of differential equations was implemented in Brian 2.0,[37]and the simulations used a fourth-order Runge–Kutta algorithm with a time step of 0.01 ms.
3.1. Magnetic field affects single neuron firing
To clarify the cellular effects of MS on neurons, we first focused on the single neuronal activity in response to MF with a fixed frequency. The MF intensity was a fixed value of 600 mT in the present study. A constant current of amplitudeIapp=0.17μA andId=0.2μA was injected into the interneuron and pyramidal neuron,respectively. Corresponding neuronal firing in response to MF injection of 50 Hz is shown in Figs.4(b)and 4(d). Both the spike times and inter-spike intervals(ISIs)of the neurons were perturbed by MF exposure.The interneuron and pyramidal cell presented regular spiking at a frequency of 4.2 Hz and 3.9 Hz, respectively, in the absence of MF exposure in Figs. 4(a) and 4(c). And the corresponding ISIs sequences distributed at a value of 248.19 ms and 281.67 ms. In the presence of MF as shown in Figs.4(b)and 4(d),the scenario could be changed. The spike frequency of the interneuron and pyramidal cell was 16.7 Hz and 6.5 Hz,respectively. The ISIs of the pyramidal cell was 160 ms, and the ISIs of the interneuron were decreased to an approximate value of 60 ms, suggesting perturbation of spike timing induced by MF exposure.[17]
Figure 5 shows the perturbance of spike count of a single interneuron and pyramidal neuron by MF at varying frequencies. Here, we can differentiate the observed neuronal spikes into two phases. Phase 1 is the subthreshold stimulus of the neuron at low frequencies with interneuron less than 4 Hz and pyramidal cell less than 20 Hz, in which the firing activities were hardly affected. In phase 2, both inhibitory and excitatory neurons were activated at higher frequencies and the spike count nonlinearly increased in a saw shape, leading to the gradual decrease of ISIs value as shown in Figs.5(b)and 5(c).Noted worthily,at frequencies 5 Hz–20 Hz,low-threshold inhibitory interneuron was activated, while the pyramidal with higher magnetic threshold cell was unaffected. These results are consistent with the experimental observation that interneurons are more sensitive to the MF due to possession of a lower magnetic threshold,[19]suggesting that interneurons and pyramidal neurons respond differently to MS.
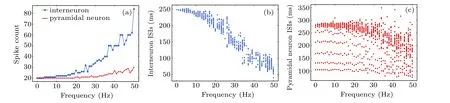
Fig.5. The spike count of single neuron in response to variation in magnetic field frequency(a)and the corresponding ISIs sequences of interneuron(b),and pyramidal neuron(c).
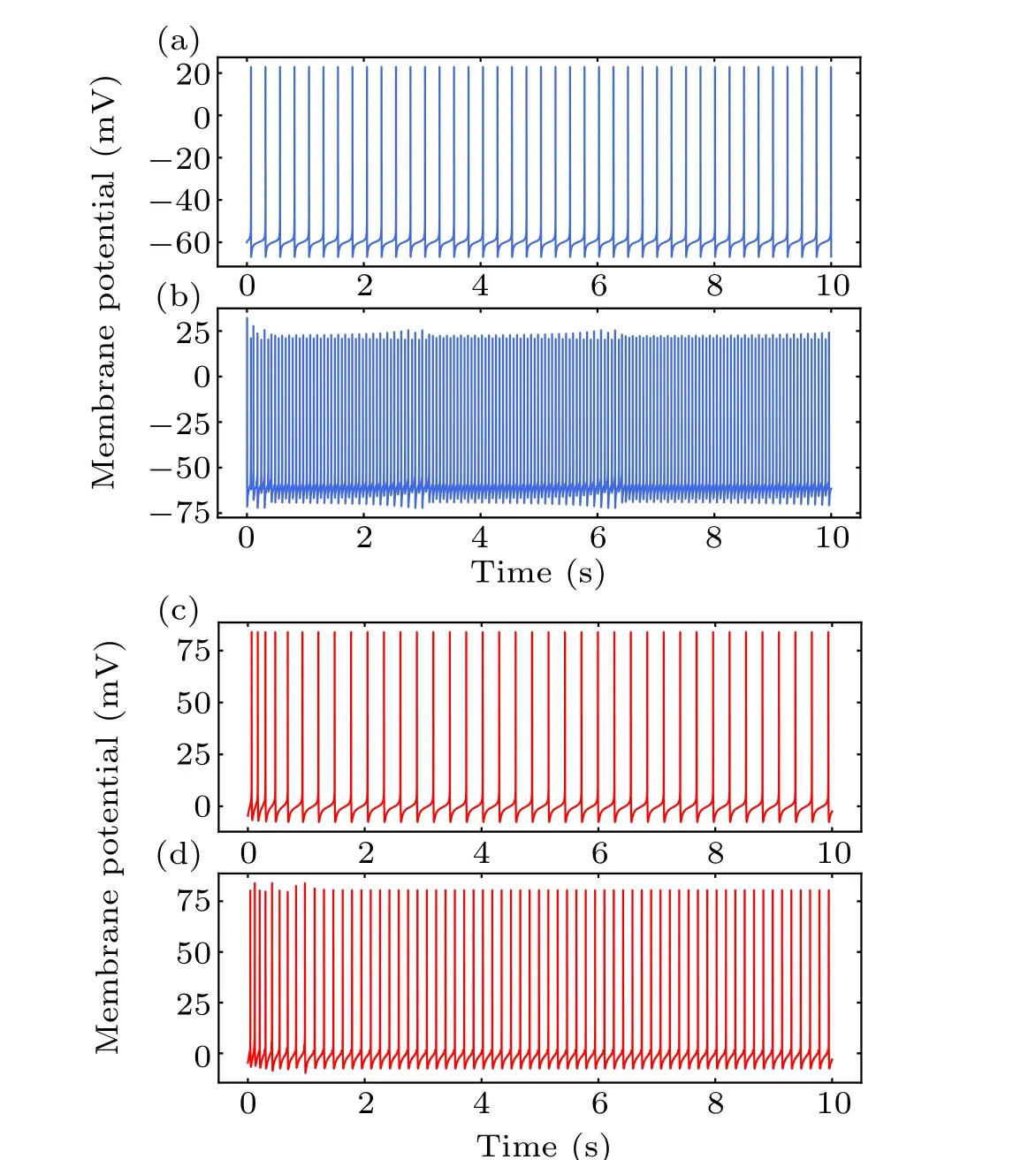
Fig.4. The membrane potential of single interneuron(blue)and pyramidal neuron(red)without(a),(c)and with magnetic field(b),(d).
3.2. Synaptic strength of coupled neurons alters the effects of magnetic stimulation
Pyramidal cell and interneuron interaction underlies hippocampal physiological function.[55]Thus, we recorded the coupled neurons in the absence of modulation of astrocytes by MS,i.e.,λ=0, overlooking the effects of astrocyte current on neurons. Changes in the firing of coupled neurons with variation in magnetic field frequency is shown in Fig.6.Although pyramidal neurons cannot be directly activated by low-frequency MF as shown in Fig.5(a),interneurons may be the primary activators of an MF and impose inhibitory input to pyramidal cells in the neuronal microcircuit through inhibitory synaptic connections. Low-frequency MS target interneuron signals, possibly corresponding to feedforward information processing. In a high-frequency MF (>25 Hz), involving a mechanism of downregulation of GABAergic action,[56]we adjusted the inhibitory synaptic conductance from 0.4 mS to 0.01 mS to decrease inhibition effect of interneuron, which resulted in a reduction in inhibitory synaptic current and pyramidal neuronal firing at high frequency, as shown in Fig. 6(black arrow). These results indicate that the effect of MS on pyramidal neurons was mediated by the action of inhibitory interneurons,[57]supporting the idea that inhibitory circuits play a vital role in the action of MS and this may contribute significantly to excitability modulation.[58]
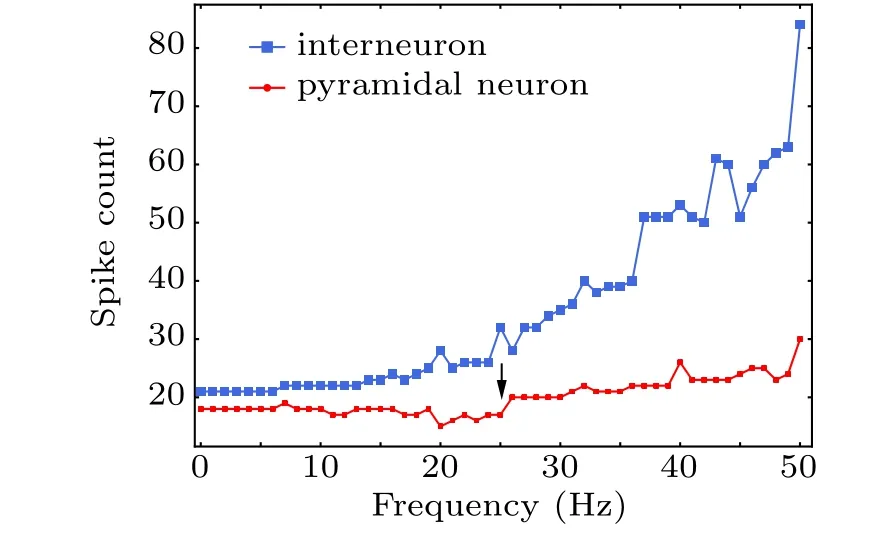
Fig.6. Spike count of coupled neurons during treatment with different magnetic field frequencies.
To further assess the influence of MF on the information transmission from an interneuron to a pyramidal cell,we tuned the synaptic coupling strength by changing the GABAaR conductance. The results with a strong conductance(0.4 mS)are illustrated in Figs.7(b)and 7(d). In this case,strong inhibitory inputs led to hard pyramidal neuron depolarization, even at high frequencies. In contrast,the presence of a weak GABAaconductance (0.01 mS) yielded a large increase in pyramidal neuronal firing and a shift in inhibition toward excitation with increasing frequency. The variation in neuronal firing may reflect either a change in the membrane excitability of pyramidal and excitatory interneurons or a change in the synaptic efficacy between neurons. These results reveal a correlation between the MF and synaptic coupling strength,suggesting that changes in synaptic strength could lead to a reduction in pyramidal neuronal excitability as a result of enhanced interneuronal excitability.
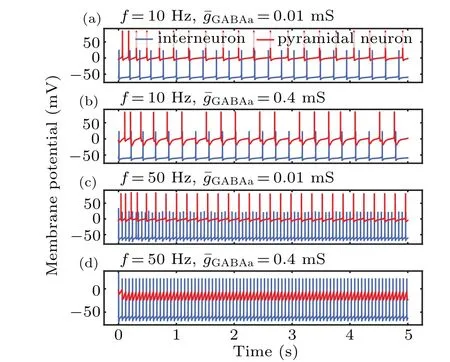
Fig. 7. Time series of membrane potential in pyramidal neurons and interneurons at different synaptic coupling strengths and magnetic field frequencies.
3.3. Magnetic stimulation increases intracellular calcium levels in astrocytes
Increased intracellular Ca2+concentration is unanimously considered a significant signal for astrocytic activity.To investigate the cellular mechanism of MF-induced Ca2+surges,we simulated the response of a single astrocytic model during MF exposure at different frequencies. The black line in Figs. 8(a) and 8(b) shows the astrocytic IP3and calcium signals evoked by glutamate release from the presynaptic terminal in physiological condition. The direct response of astrocytes during MF exposure without neuronal modulation is shown in Fig.8(colored lines),in which we omitted the production of synaptically induced IP3. The single astrocyte in this case is impervious to neuronal action potentials and can be thought of as a purified astrocyte in culture. In contrast to glutamate-activated astrocytes,it can be seen that MF-evoked calcium surges occurred in a faster manner at higher amplitudes. Consistent with previous reports,[21]we found a significant increase in the Ca2+concentration during treatment with different MF frequencies. These results illustrate involvement of the MF in the modulation of astrocyte Ca2+signals and support frequency-dependent effects of MF on astrocytes. Therefore, activation of a single astrocyte by an MF is sufficient to induce Ca2+elevation,thereby releasing gliotransmitters to regulate neurons.
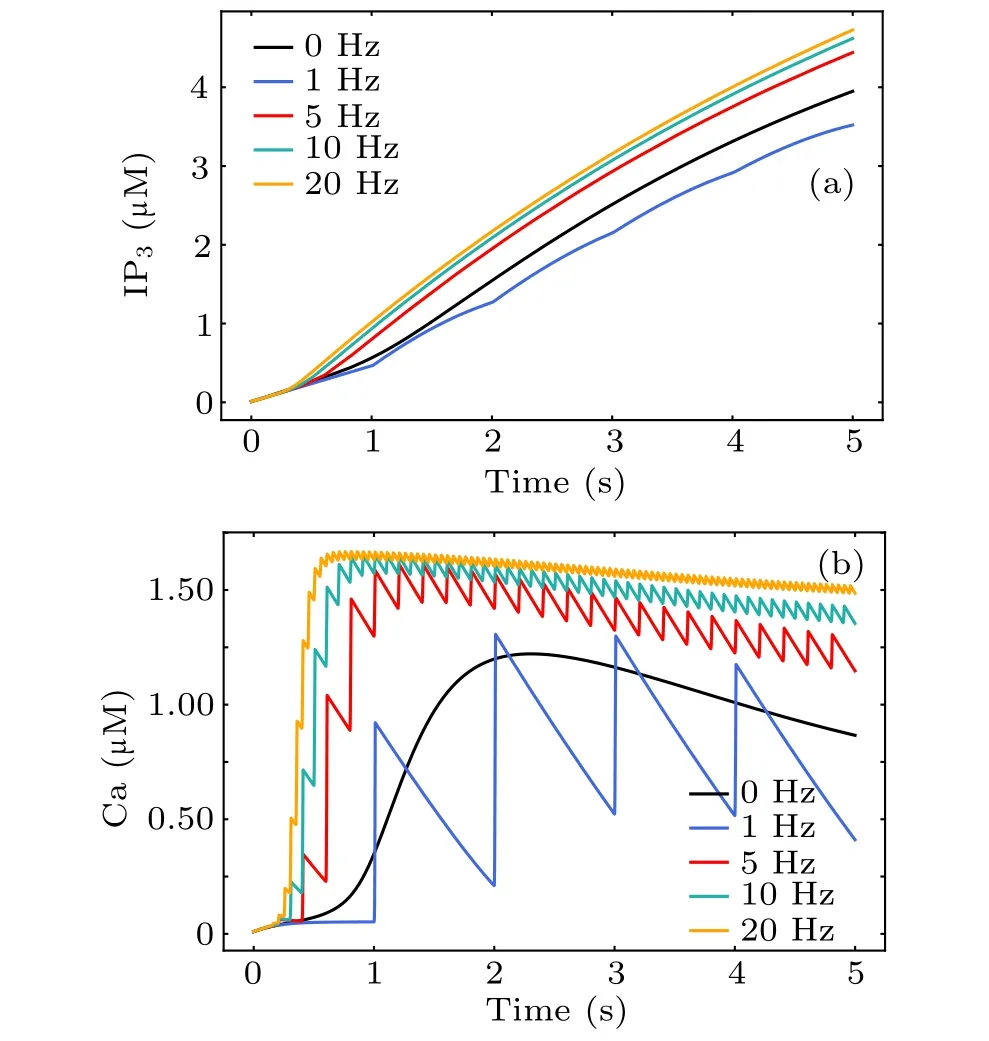
Fig.8. The dynamical response of astrocytic IP3 (a)and Ca2+ (b)to magnetic stimulation during treatment with different magnetic field frequencies.
3.4. Astrocytes can either enhance or decrease neuronal activity at different magnetic field frequencies
A schematic of the neural–astrocyte circuit is presented in Fig. 1. When astrocytes are involved in the neural–astrocyte microcircuit, the situation becomes more complicated. The slow inward currentIsicare mediated by astrocytic ATP and glutamate,which can activate interneurons and pyramidal cells to form feedback loops, respectively. In principle, these two independent routes lead to multiple possible scenarios to regulate the strength of neuronal responses via critical parametersλGluandλATP. For the sake of clarity, we restricted our attention to the simpler cases of the presence or absence of the astrocytic glutamate and ATP signaling pathways. There are three cases of neuronal modulation: glutamatergic gliotransmission (λATP=0) and ATP gliotransmission (λGlu=0) and co-existing gliotransmissions.
Astrocyte interacts with both pyramidal neurons and interneurons to regulate their excitability under different stimulation paradigms. Depending on the value of the parametersλGluandλATP,Iastroinduced by astrocytic gliotransmitters can either increase or decrease pyramidal neuronal excitability. Following the release of astrocytic glutamate (λGlu=1,λATP=0), the firing of pyramidal neurons in this case was strongly augmented as shown in Figs. 9(a) and 9(d). Such an increase in excitability may counteract (at least partly)the resulting boost in interneuronal firing triggered by lowfrequency MS in Figs.9(c)and 9(f). The opposite effect was observed forλATP=1,λGlu=0 in Figs. 9(b) and 9(e). ATP released from astrocytes excites interneurons, resulting in increased synaptic inhibition within intact hippocampal circuits.Astrocyte-enhanced inhibition of pyramidal neuron through interneuron partly counteracts MS-enhanced excitation,which prevents pyramidal neurons from overfiring at high frequency MS. Astrocytes may play a critical role in circuit function of the hippocampus by modulating the activity of interneurons and pyramidal neurons.In addition,these results show that the calcium dynamics in astrocytes strongly affect neural activity.These data provide a case for the involvement of astrocytes in mediating this effect of MS on neuronal excitability. Astrocytes are one of the key regulators of neuronal excitability and synaptic functions, exerting a powerful action on excitation–inhibition balance.[59]
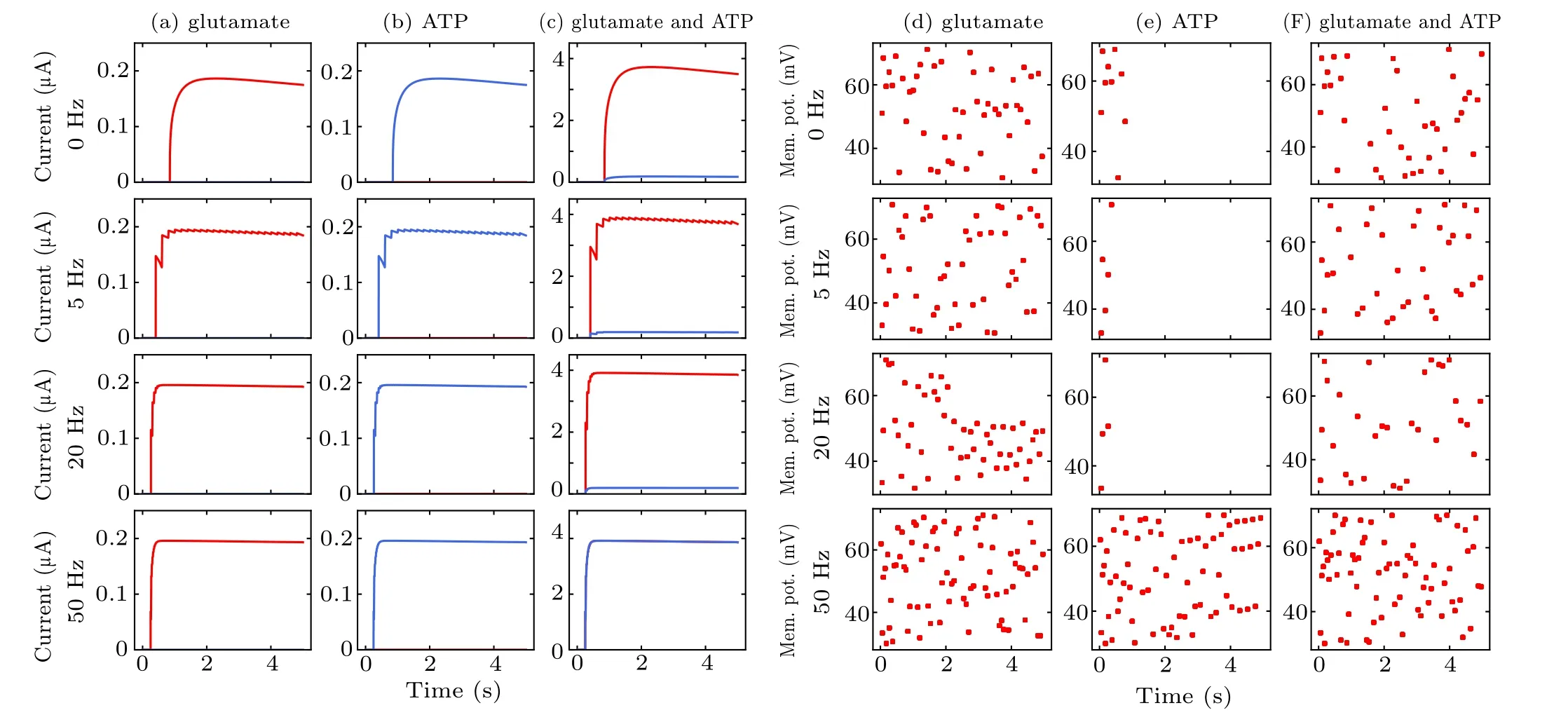
Fig.9. Variations in SIC and neuronal spike during the three cases of modulation by astrocyte-derived glutamate(a),(d),astrocyte-derived ATP(b),(e)and co-existing condition (c), (f). The dots in (d)–(f) represent each pyramidal neuron spike event. Interneuron firing is omitted for clarity. The abbreviation“Mem. pot.” in the figure represents membrane potential.
4. Discussion and conclusion
A growing body ofin vitroandin vivoevidence collected over recent decades strongly suggests that astrocytes play a vital role in neuronal excitability and synaptic transmission,giving important insight into the possible mechanism underlying MS.However,the functional details of astrocytic modulation of neurons from experimental data using MS remain to be elucidated and demand both experimental and numerical modelings. In the present study, we developed a neural–astrocyte microcircuit computational model based on experimental results obtained in the hippocampus with a view to uncovering the function and responsiveness of non-neuronal cells to MS.This is an important issue regarding the mechanism of MS on brain tissue,and the results presented herein provide important clues to the involved signaling machinery.
The numerical results of our model disclose multiple key factors that affect the efficacy of MS in neural–astrocyte microcircuits, yielding several predictions. First is the observation that interneurons and pyramidal neurons have different magnetic thresholds of activation. This is likely due to morphological and structural differences,such as ion channels and the number of dendrites,leading to different responses of neurons to different frequencies of MF.[19]The second prediction arises instead from analysis of the coupled neurons, in which the interneurons have a strong influence on pyramidal neuronal output firing by generating IPSC.In accordance with our previous experimental observations during TMS treatment on cerebellar slices utilizing the MultiElectrodes Array (MEA)system,[60]the model reproduced the general pattern of inhibition at low frequencies and excitability at high frequencies;however,the frequency ranges are not exactly consistent. This may be due to the large difference in the number of synaptic connections between our model and physiological conditions.In fact, the neuronal response to MS depends on the state of network activity.[61]These results demonstrate that the effect of MS correlates with cell type and network state.[9]
It is well accepted that fluctuations in Ca2+concentration are important measurements of astrocytic activity and result from the influx of extracellular[Ca2+]ovia plasma membrane transit and the release of intracellular[Ca2+]ifrom internal stores. MS may influence astrocytic calcium regulation in both ways.[21,22]Although the mechanism remains to be elucidated,our results suggest that by changing the parameters of MS,astrocyte Ca2+activity can directly respond to an MF,influencing the dynamics of Ca2+and hence Ca2+homeostasis.The kinetics and amplitudes of the MS-evoked Ca2+signals differed from spontaneous astrocytic activity,[62]in which astrocyte Ca2+events occur in a slow and prolonged manner under physiological conditions.[63]This is likely due to the full intracellular cascade in astrocytes requiring successive events including receptor activation, second messenger IP3production, and astrocyte Ca2+elevation, whereas an MF can directly regulate ion channel activity.[35]Nevertheless,there are no experimental data available to precisely quantitate the coupling changes in IP3R and Ca2+channels during MF exposure,which may have broad implications for astrocyte Ca2+concentration and neuron–glia communication.[64]Further experimental studies are required to elucidate the exact mechanism of Ca2+release from intracellular stores during MS.
Another significant prediction of our modeling framework is that MF produces an activity-dependent biological effect on astrocytes. Astrocytes immersed in the circuits can decode external stimuli and exert diverse modulatory actions to influence synaptic transmission in multiple forms.This is consistent with experimental observations and numerical results in the hippocampus,[49,65]where astrocyte-released gliotransmitters can transiently decrease or increase the synaptic response to stimulation. Therefore,we can conclude that the existence of astrocytes is a crucial condition for the neuronal excitation–inhibition balance,especially following disturbance by an external MF.In fact,the therapeutic effect of TMS in counteracting depression or epilepsy has been largely attributed to the potentiation of glutamatergic or GABAergic transmission.[66,67]The calcium dynamics of MF activation in astrocytes strongly affect neural activity;accordingly,an intervention of the Ca2+signaling pathway in astrocytes may be a potential therapeutic target of MS for certain neurogenic diseases.
Overall, the modeling studies performed in the present paper provide valuable information regarding the mechanism of action of MS on cells, including the interaction between neurons and astrocytes. Our future work will focus on modeling pathological conditions to investigate individual neuronal and network properties during and after the application of TMS protocols.
- Chinese Physics B的其它文章
- Coarse-grained simulations on interactions between spectrins and phase-separated lipid bilayers?
- Constraints on the kinetic energy of type-Ic supernova explosion from young PSR J1906+0746 in a double neutron star candidate?
- Gas sensor using gold doped copper oxide nanostructured thin films as modified cladding fiber
- Exact explicit solitary wave and periodic wave solutions and their dynamical behaviors for the Schamel–Korteweg–de Vries equation?
- Suppression of ferroresonance using passive memristor emulator
- Suppression of ice nucleation in supercooled water under temperature gradients

