劉靖子喆,張文鵬

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言

眾所周知,Fibonacci序列{Fn}為

F0=0,F1=1,Fn=Fn?1+Fn?2(n≥2).

改變它的初始項(xiàng),即得到Lucas序列{Ln}:

L0=2,L1=1,Ln=Ln?1+Ln?2(n≥2).

文獻(xiàn)[1]研究了關(guān)于Fibonacci序列{Fn}和Lucas序列{Ln}的一些二項(xiàng)式系數(shù)和的恒等式.

文獻(xiàn) [2]考慮了關(guān)于雙周期 Fibonacci序列和雙周期 Lucas序列的一些二項(xiàng)式系數(shù)和的恒等式.文獻(xiàn)[3]進(jìn)一步研究了關(guān)于廣義雙周期Fibonacci序列和廣義雙周期Lucas序列的一些二項(xiàng)式系數(shù)和的恒等式.

因此,自然地希望得到關(guān)于廣義三周期Fibonacci序列和廣義三周期Lucas序列的二項(xiàng)式系數(shù)和的恒等式.設(shè)a,b,c,d都為實(shí)數(shù).廣義三周期Fibonacci序列{un}定義為

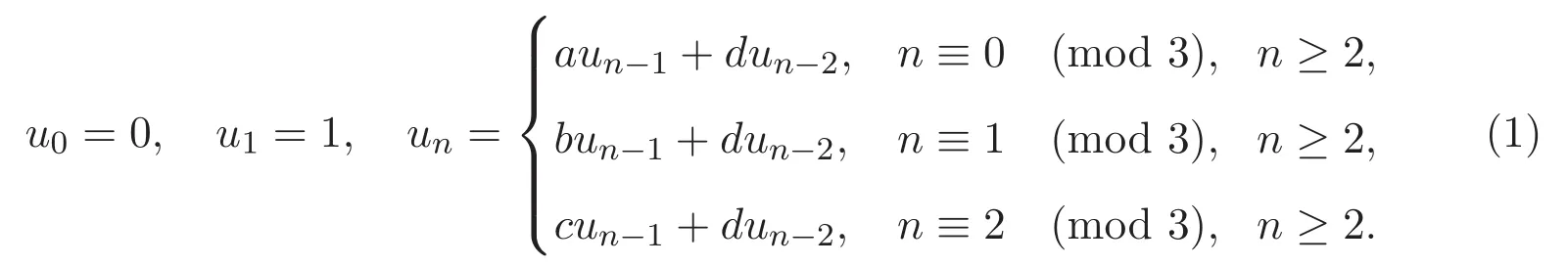
對(duì)應(yīng)地,廣義三周期Lucas序列{vn}表示為

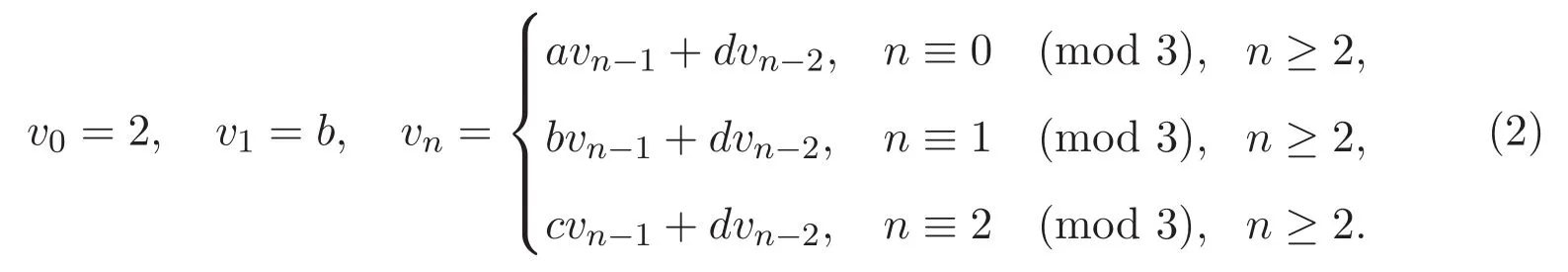
矩陣方法對(duì)于研究Fibonacci序列的恒等式是非常有用的,如文獻(xiàn)[4-5].它在本文的討論中也起著重要的作用.

本文第二節(jié)構(gòu)造了廣義三周期Fibonacci序列{un}的通項(xiàng)公式.第三節(jié)中,在一定限制條件下,利用矩陣方法在給出一系列性質(zhì)之后,得到了關(guān)于廣義三周期Fibonacci序列和廣義三周期Lucas序列的一些二項(xiàng)式系數(shù)和的恒等式.

2 廣義三周期 Fibonacci序列的通項(xiàng)公式

在本節(jié)中,構(gòu)造廣義三周期Fibonacci序列的通項(xiàng)公式.

由文獻(xiàn)[6]可知,廣義三周期Fibonacci序列{un}的生成函數(shù)為

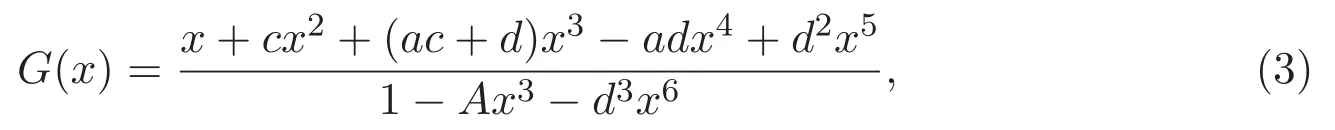
其中A=abc+ad+bd+cd.

定義

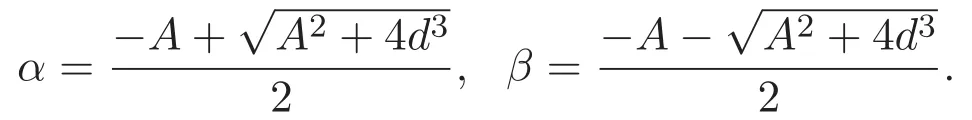
要求A2+4d30,即α,β是 x2+Ax?d3=0兩個(gè)不同的根.有下列性質(zhì):

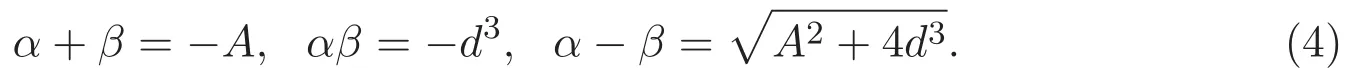
定理 2.1 廣義三周期Fibonacci序列{un}的通項(xiàng)公式為

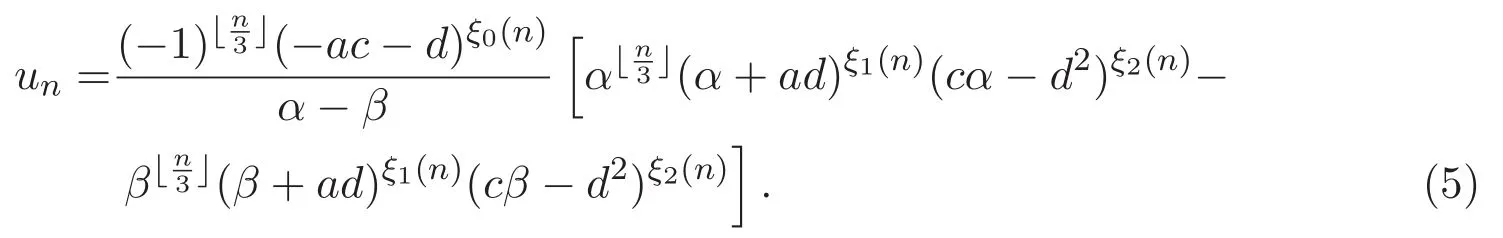
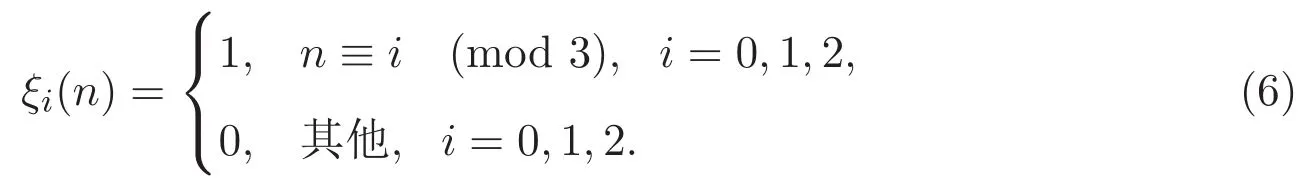
證明 對(duì)生成函數(shù)G(x)作部分分式分解,得到

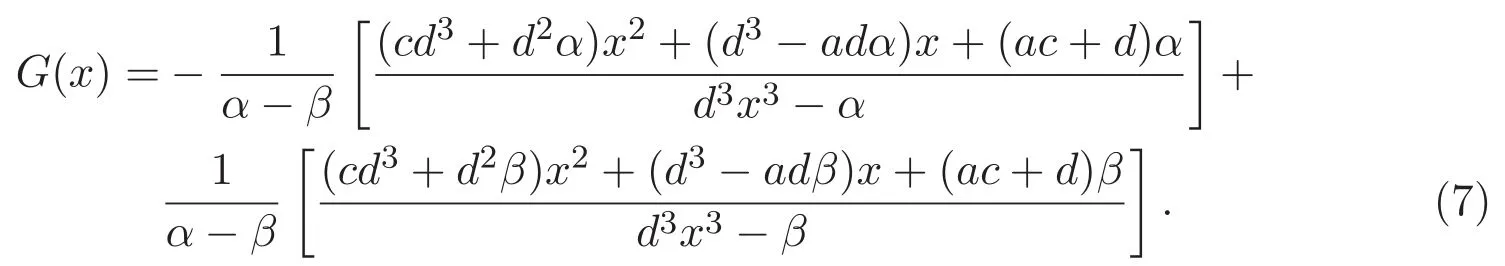
計(jì)算冪級(jí)數(shù)展開(kāi)式,G(x)可化為

其中

同理可得

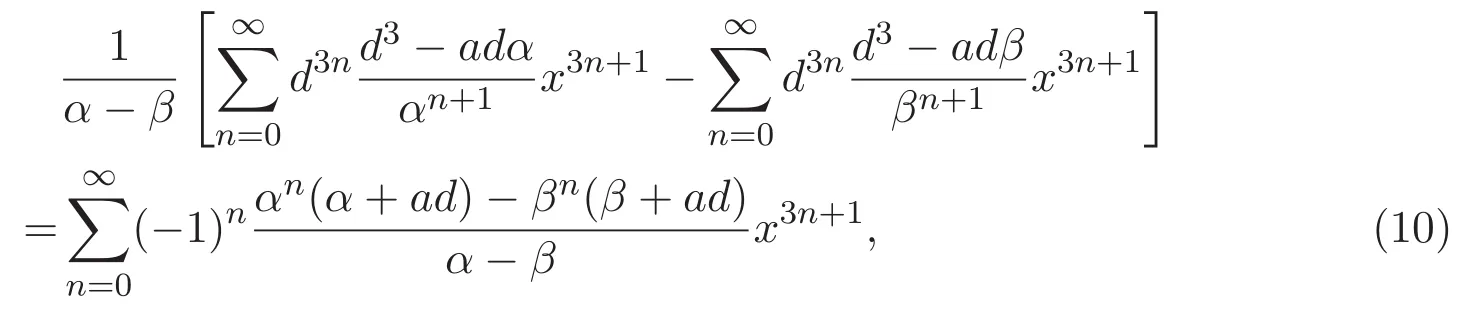
和

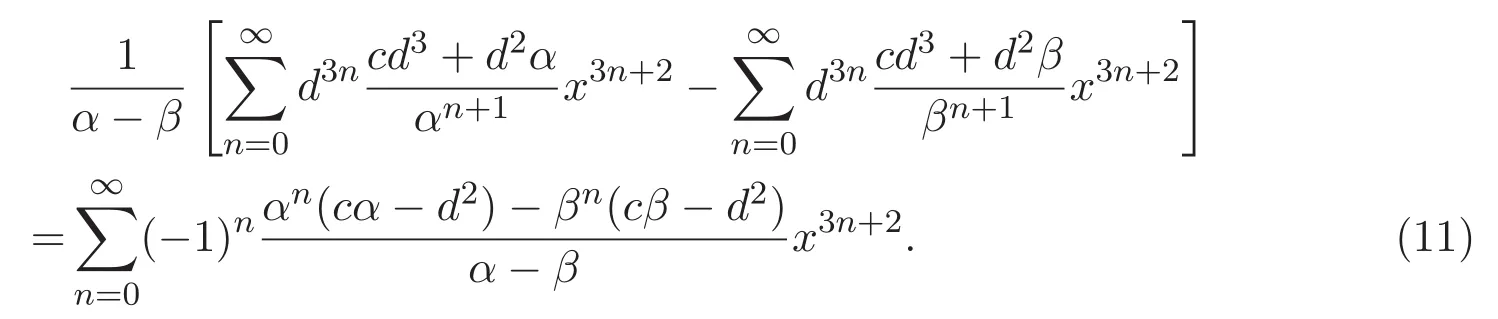
結(jié)合(9)-(11)式,得到

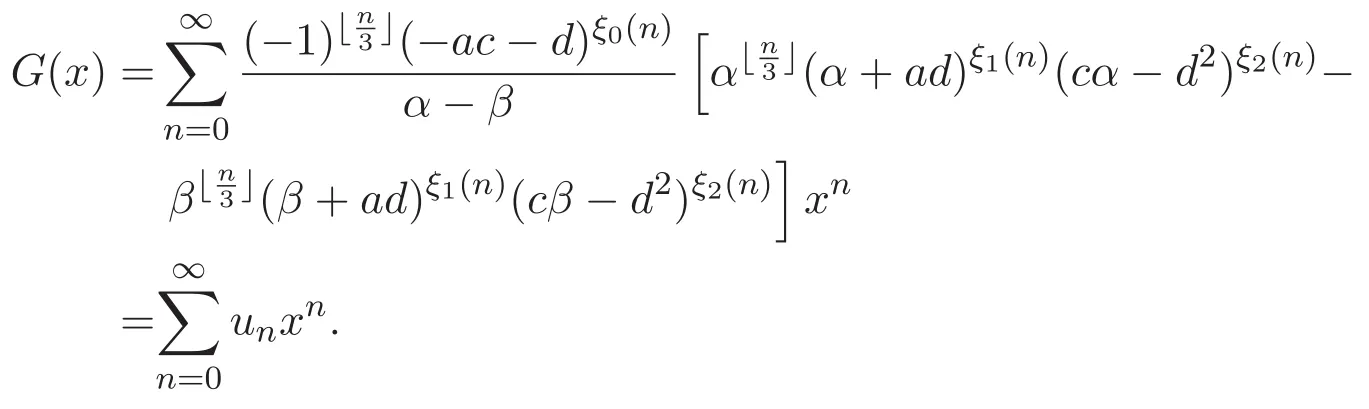
因此得到(5)式.證畢.

用相同的方法,得到廣義三周期Lucas序列{vn}的通項(xiàng)公式

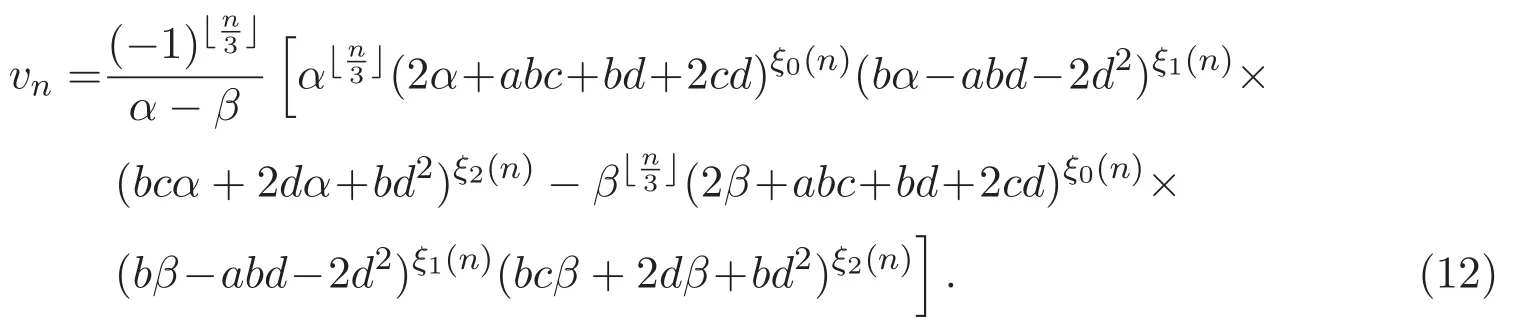
3 關(guān)于廣義三周期Fibonacci序列的二項(xiàng)式系數(shù)和的恒等式

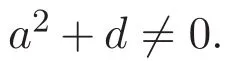
首先注意到此時(shí)A=a2b+bd+2ad.

由 (4)式 α+β=?A,可知 α?β=2α+A,β?α=2β+A.則

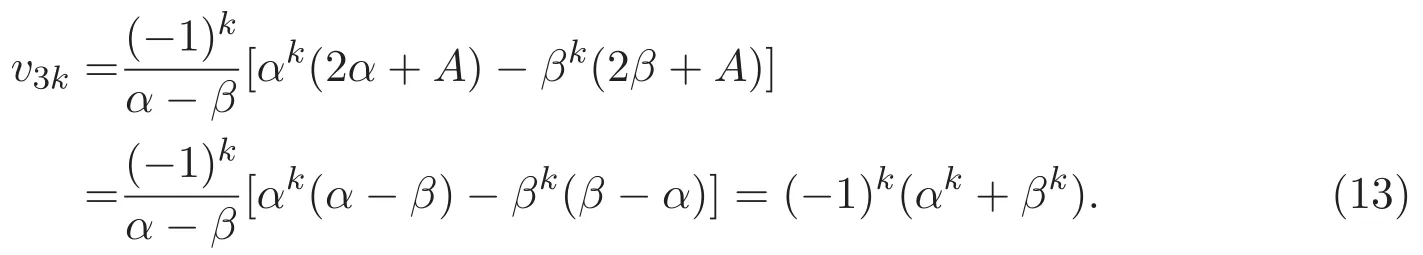
引理 3.1 設(shè)非負(fù)整數(shù)m和n至少有一個(gè)被3整除,則有恒等式:

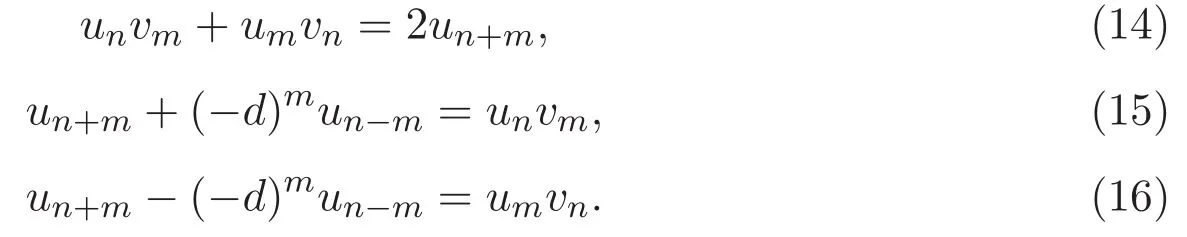
證明 僅給出(16)式中n=3k,m≡1(mod 3)的情形,其他情形方法相似,在此從略.當(dāng)n=3k,m≡1(mod 3)時(shí),

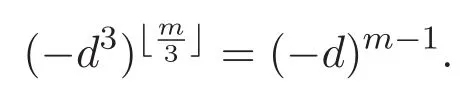
由(13)式得到

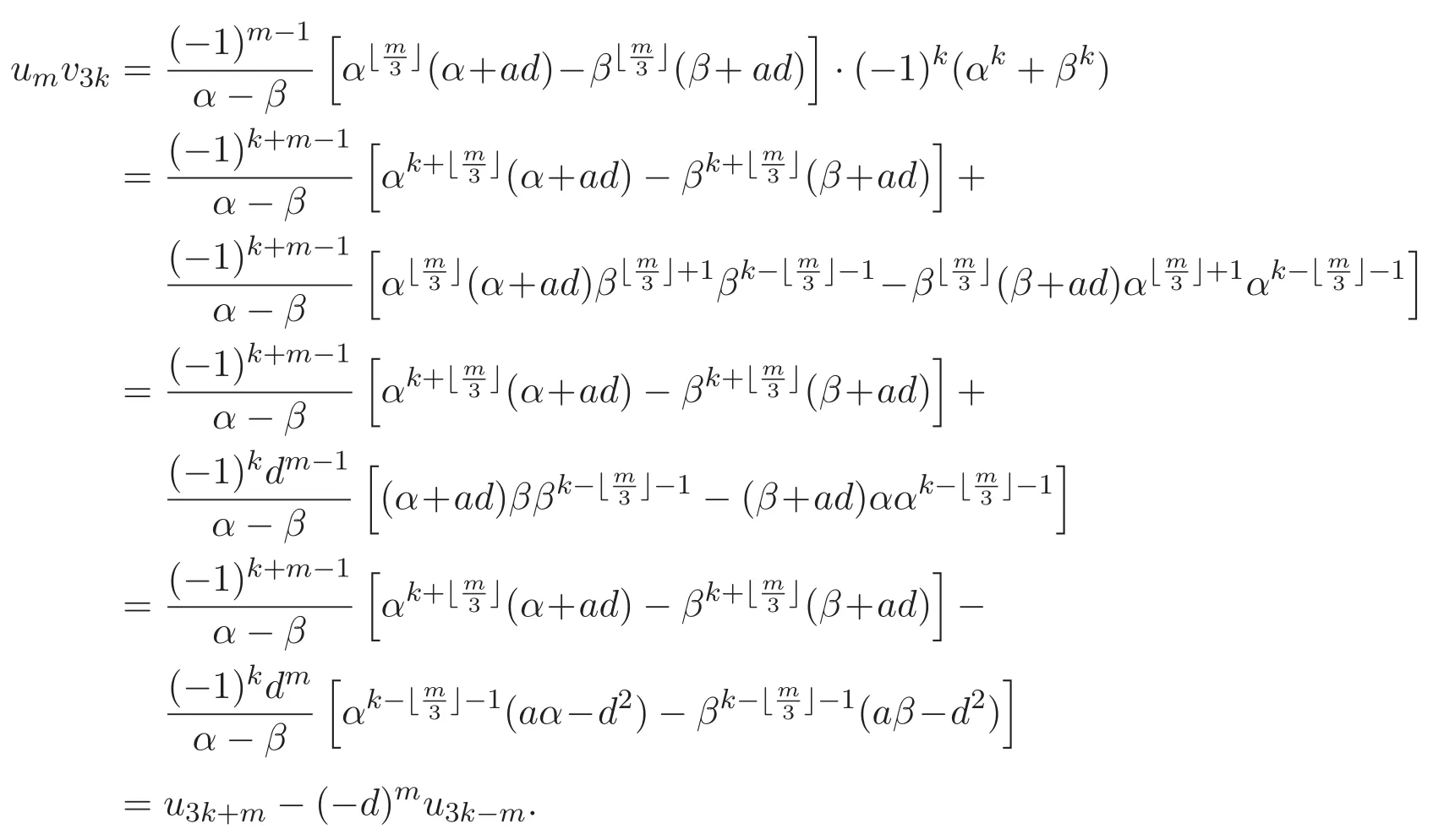
證畢.

對(duì)于任意正整數(shù)k,定義2×2矩陣

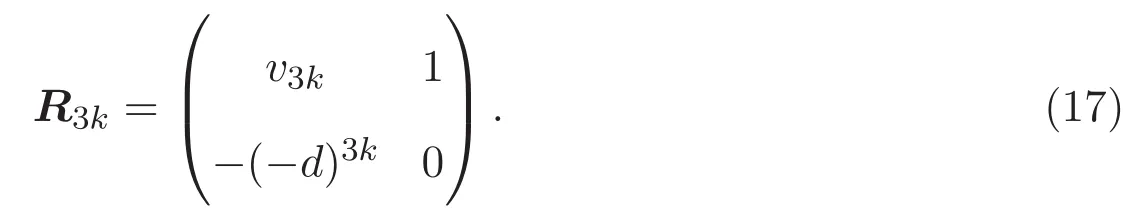
要求 a2+d0,確保了 u3k0.因此有如下引理:

引理 3.2 對(duì)于非負(fù)整數(shù)n,有

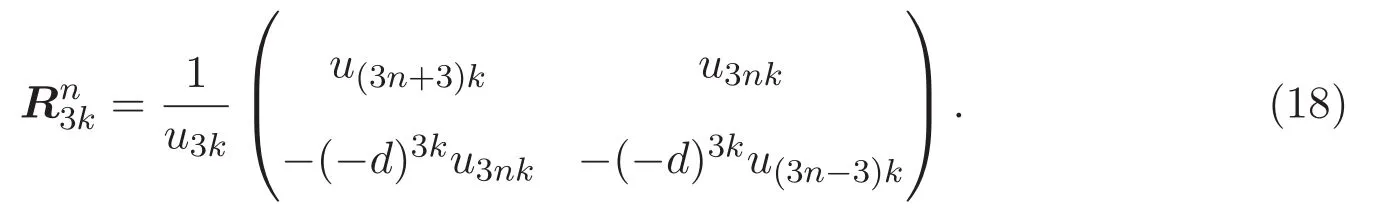
證明 使用數(shù)學(xué)歸納法.當(dāng)n=1時(shí),由(14)式知,顯然成立.假設(shè)(18)式對(duì)于任意正整數(shù)n成立,只需證明(18)式對(duì)于n+1成立即可.由(15)式知,

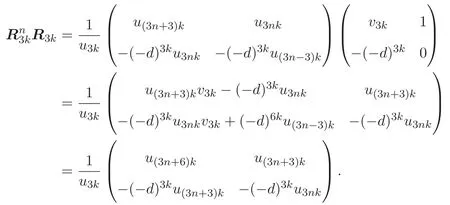
因此(18)式對(duì)于n+1成立,證畢.

引理 3.3 設(shè)m,n和q為非負(fù)整數(shù),且m和n被3整除.則

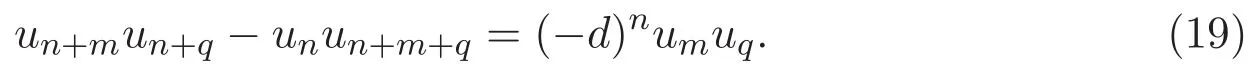
證明 對(duì)于n=3k,m=3p,q≡1(mod 3),有

對(duì)于q≡0(mod 3)和q≡2(mod 3)的情形,同理可證.

由引理3.3,直接得到

推論 3.1 設(shè)k為非負(fù)整數(shù),整數(shù)t≥3k.則有

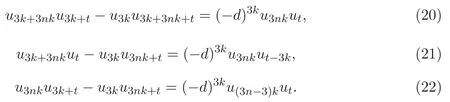
對(duì)于整數(shù)t≥3k,定義 2×2矩陣Pt為

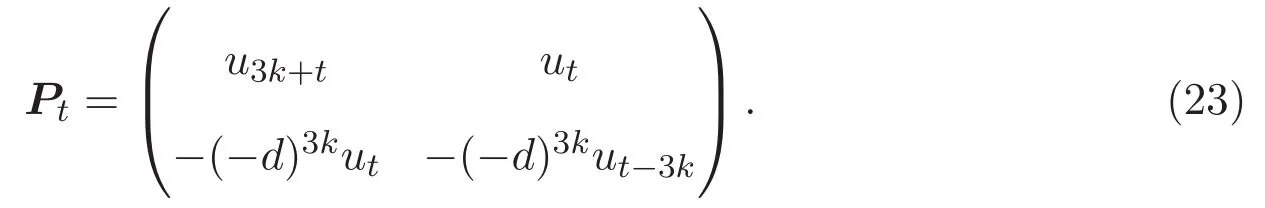
由(20)-(22)式以及引理3.2,計(jì)算得到

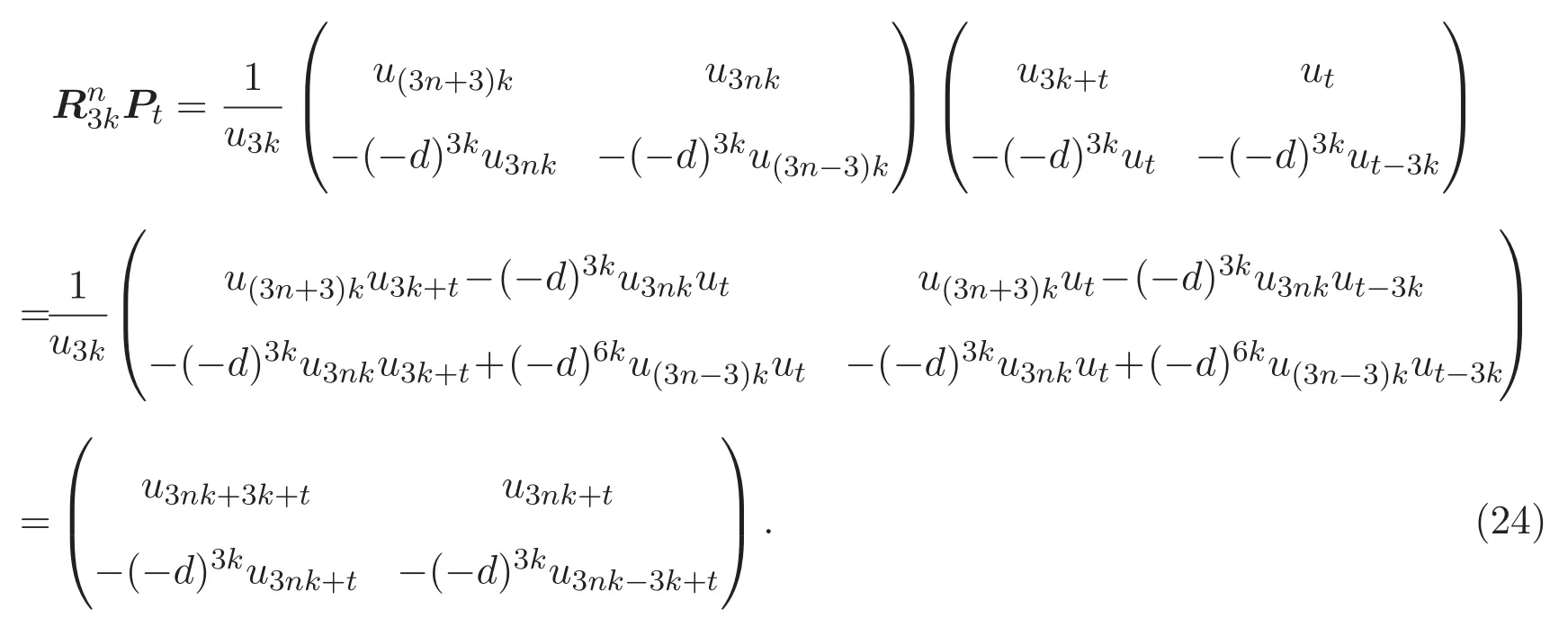
由Cayley-Hamilton定理知,矩陣R3k的特征方程為

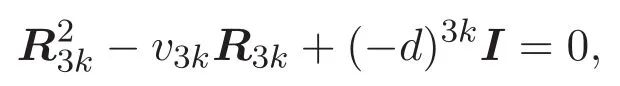
其中I為二階單位矩陣.因此

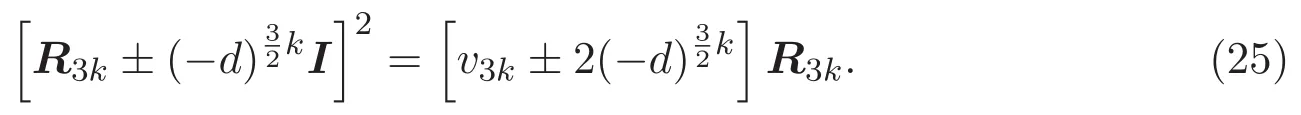
引理 3.4 對(duì)于非負(fù)整數(shù)k,則有

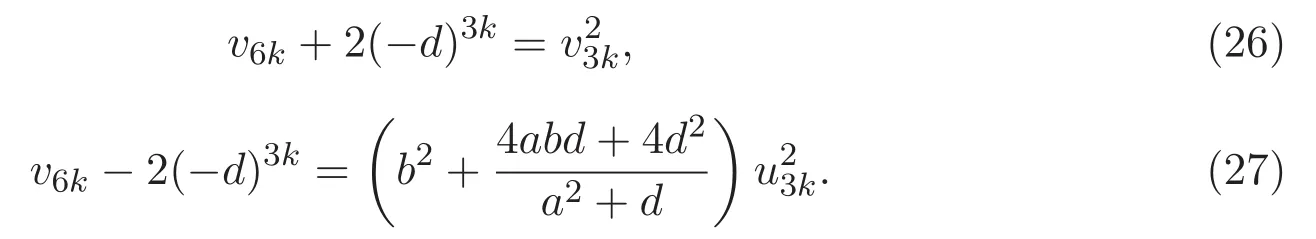
證明 對(duì)于(26)式,由(14)式可知

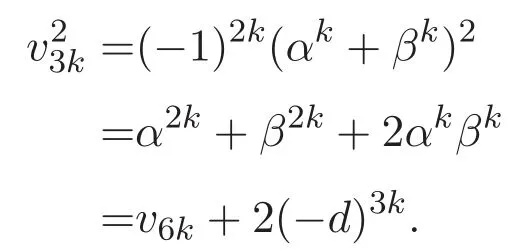
對(duì)于(27)式,得到

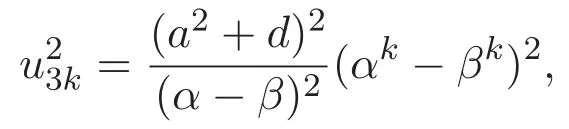
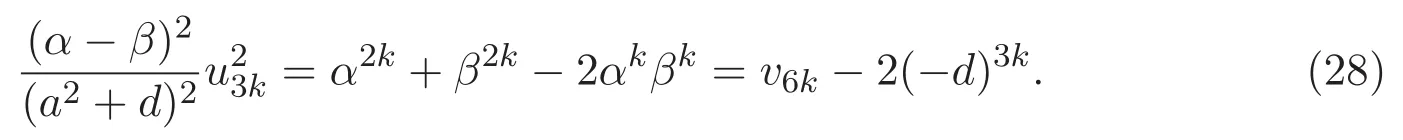
由(4)式知,

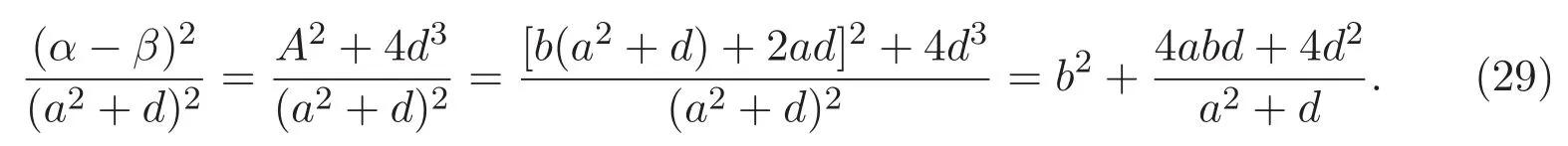
結(jié)合(28)-(29)式,即得(27)式.證畢.

定理 3.1 設(shè)m,n和k為非負(fù)整數(shù),則有如下矩陣恒等式:

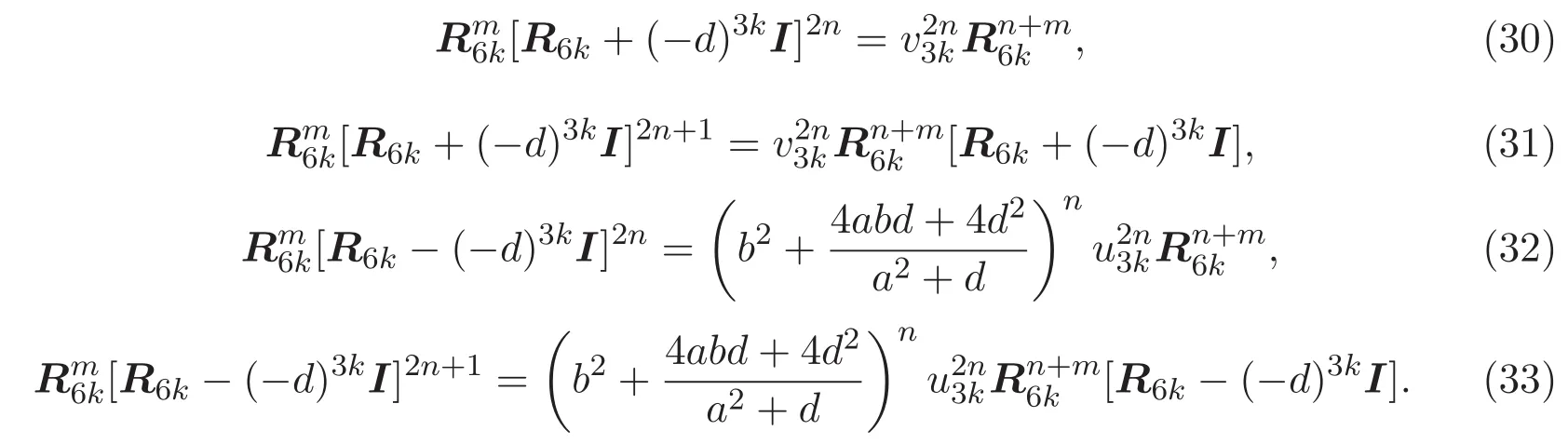
證明 僅證明(31)式.其他三式方法相似,在此從略.由引理3.4和(25)式,得到

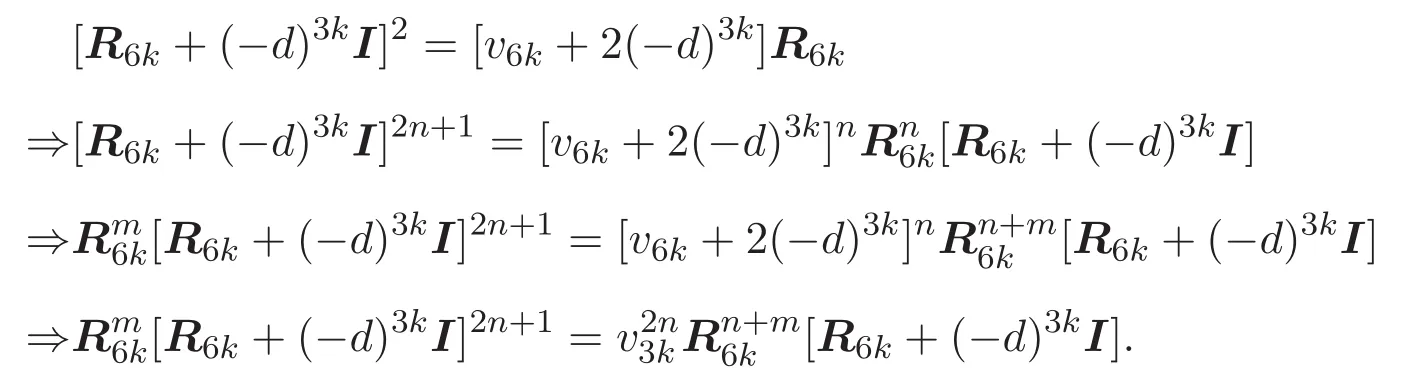
證畢.

定理 3.2 設(shè)m,n和k為非負(fù)整數(shù),整數(shù)t≥3k.則下列二項(xiàng)式系數(shù)和的恒等式成立:

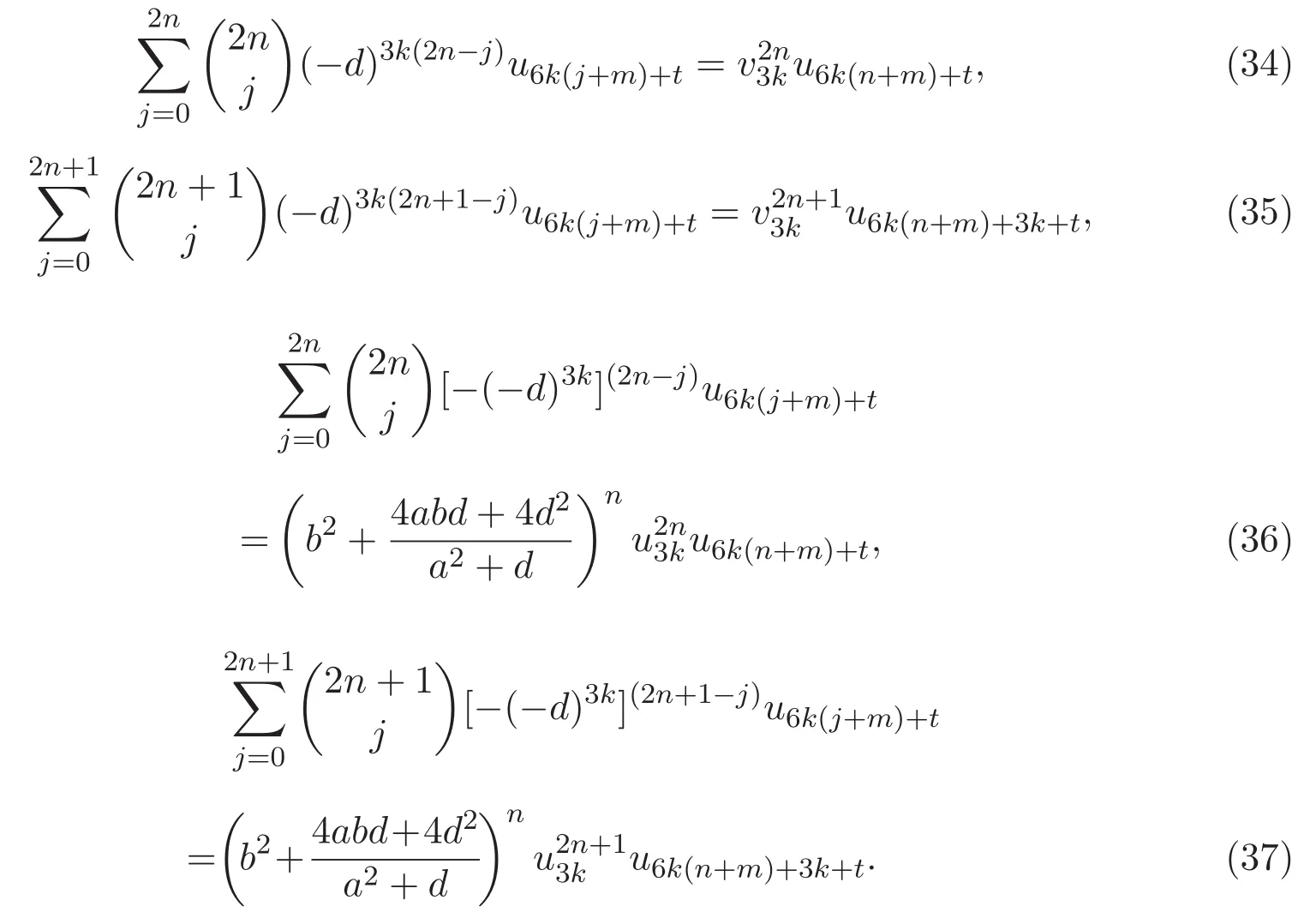
證明 同樣僅證明(35)式.對(duì)(31)式進(jìn)行二項(xiàng)式展開(kāi),有

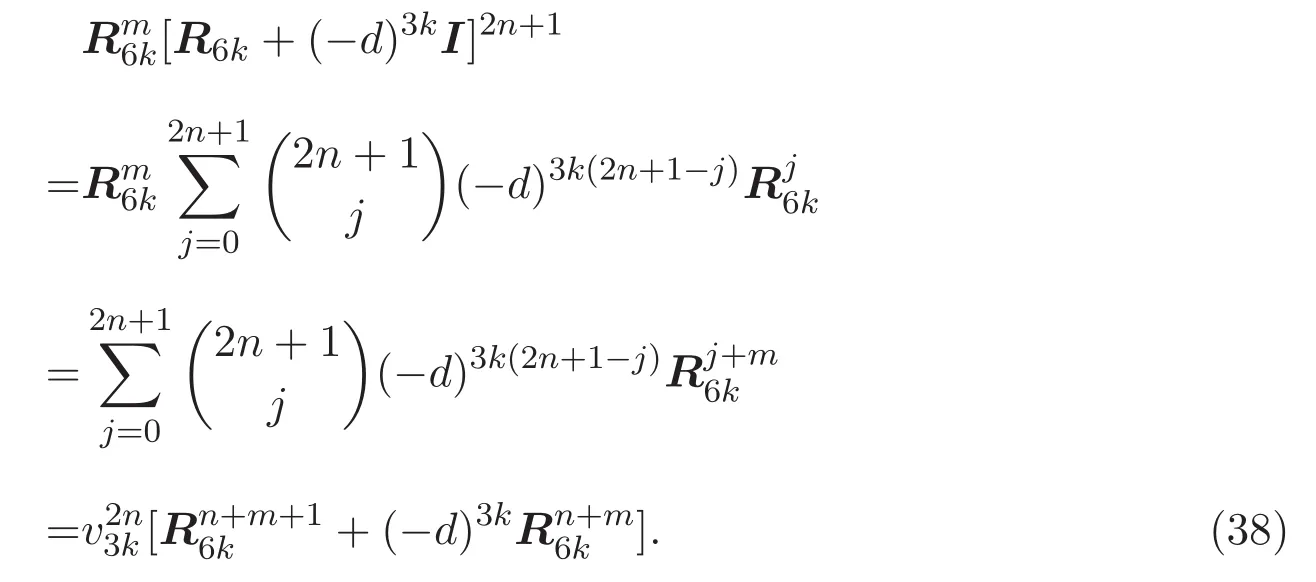
對(duì)(38)式最后一個(gè)等號(hào)兩端右乘矩陣Pt,左右兩端所得矩陣右上角元素對(duì)應(yīng)相等,再結(jié)合(15)式,得到

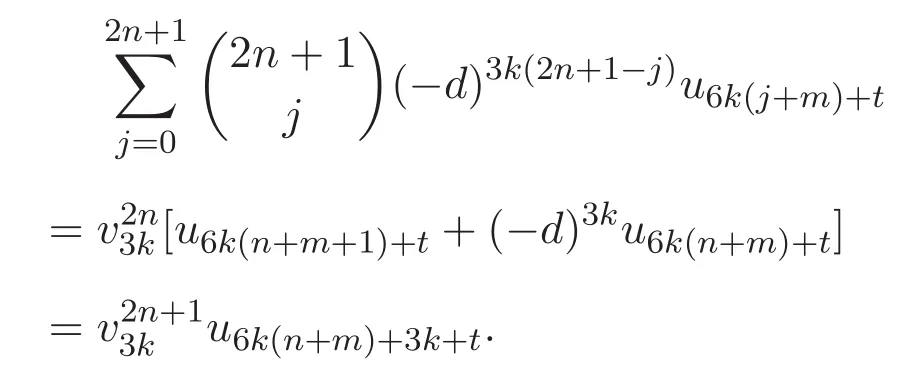
證畢.