邱凱捷,楊勝良

(蘭州理工大學(xué)理學(xué)院,甘肅 蘭州 730050)

1 引言

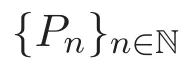
許多學(xué)者從不同的角度對Pell數(shù)進(jìn)行了研究.文獻(xiàn)[1]用Riordan矩陣來計(jì)數(shù)三種不同的Pell路,且這些Riordan矩陣的行和就是Pell數(shù).本文主要在文獻(xiàn)[1]的基礎(chǔ)上,對第3類Pell路添加新步伐,得到幾種新格路,并得出相應(yīng)的Riordan矩陣,以及這些矩陣行和滿足的遞推關(guān)系.下面給出本文要用到的定義以及相關(guān)定理.

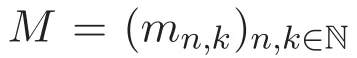
Riordan矩陣的集合在其乘法法則下構(gòu)成一個(gè)群.Riordan群的乘法法則如下:

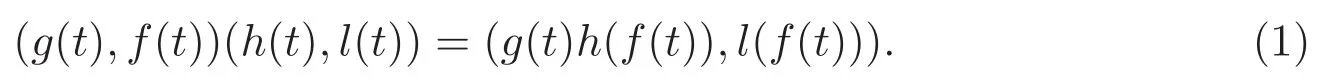
引理 1.1[3-4]設(shè) M=(g(t),f(t))為一個(gè) Riordan矩陣,D=(d0,d1,d2,···)T是一個(gè)列向量,則M 和D的乘積也是一個(gè)列向量,且發(fā)生函數(shù)為

這里的d(t)是列向量D的發(fā)生函數(shù).

由引理1.1可得以下關(guān)于Riordan矩陣的一條重要性質(zhì):

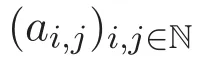
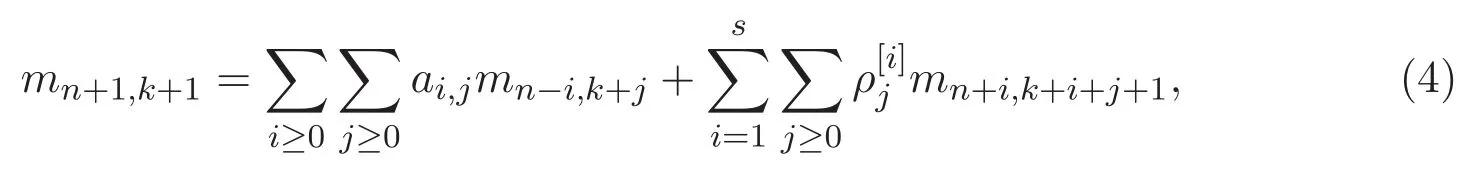
若Φ[i](t)表示A-矩陣的第i行的發(fā)生函數(shù),Ψ[i](t)表示序列

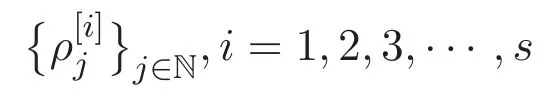
的發(fā)生函數(shù),則f(t)可以定義為

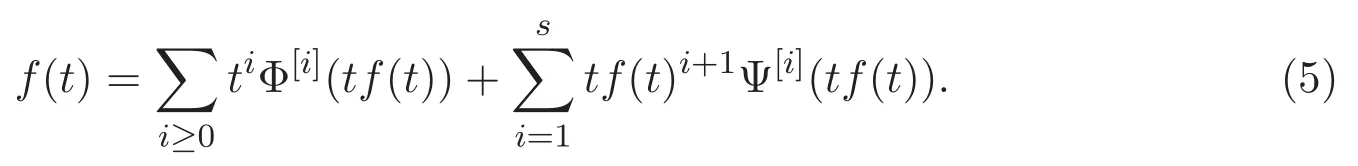
若Riordan矩陣M的第0列定義為

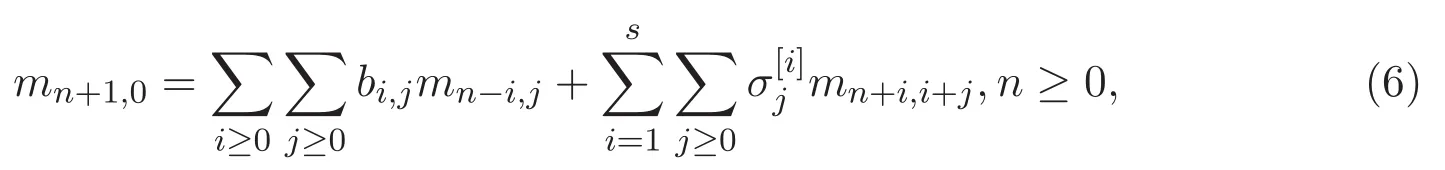
則g(t)可由以下公式得到

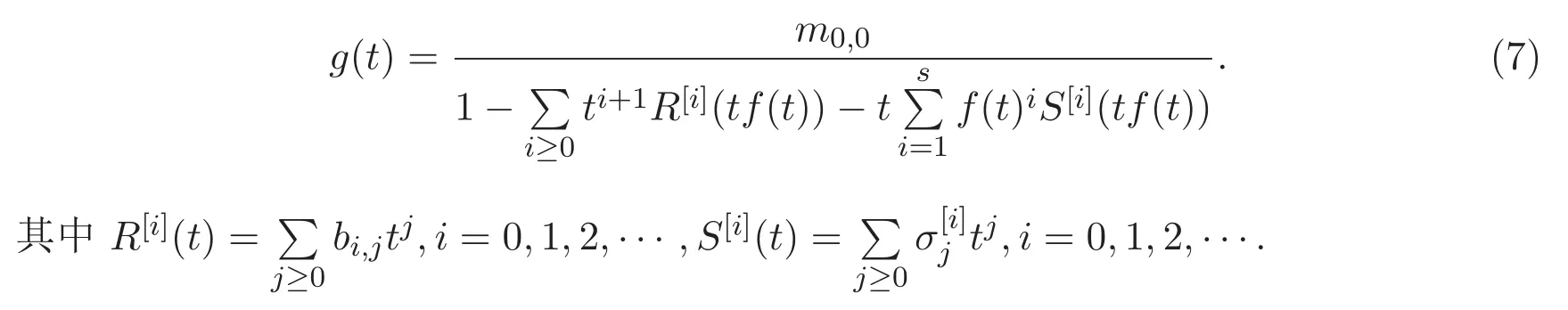
2 Riordan矩陣和 Pell數(shù)

本文利用Riordan矩陣的A-矩陣,討論了Pell路滿足的Riordan矩陣,及該矩陣的行和是Pell數(shù),在此基礎(chǔ)上將格路限制在對角線上方得出其Riordan矩陣的一般表達(dá)式.

設(shè)C是從(0,0)到(n?k,k)使用步伐為(0,1),(1,0)及(2,0)的格路組成的集合,C中的格路稱做Pell路,cn,k是C中元素的個(gè)數(shù).cn,k的前幾項(xiàng)的值如表1所示:

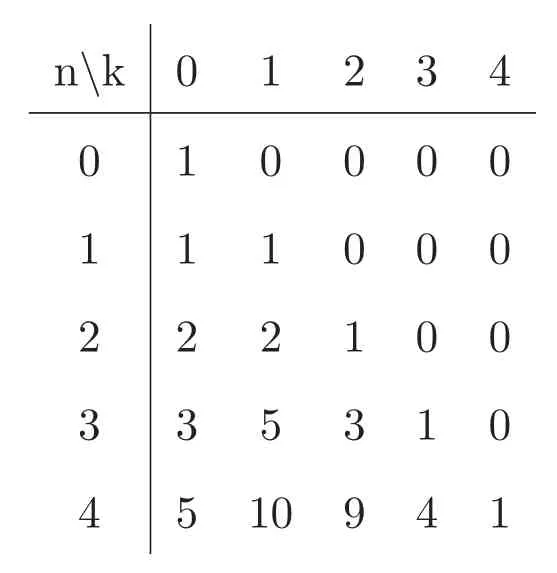
表1 矩陣C的前幾項(xiàng)的值

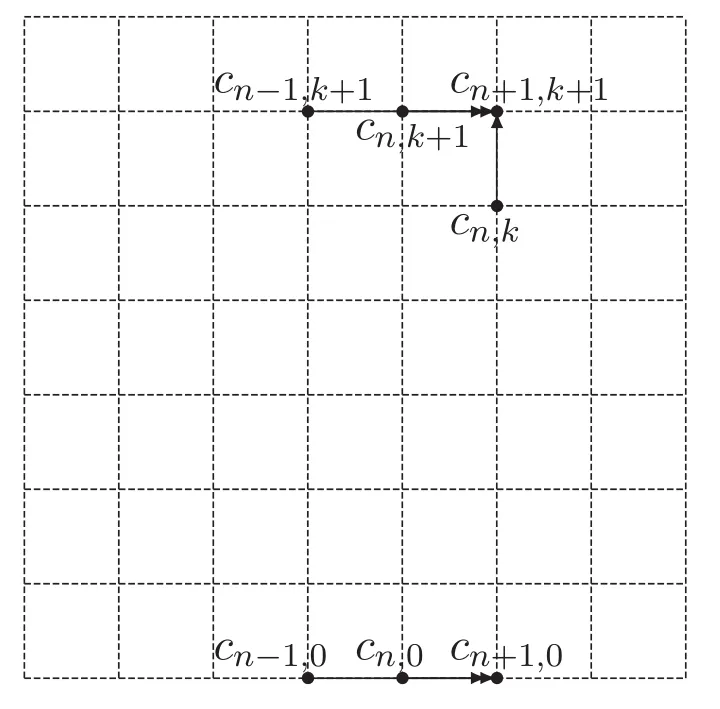
圖1 矩陣C的遞推關(guān)系

由圖1可知cn,k滿足如下遞推關(guān)系:

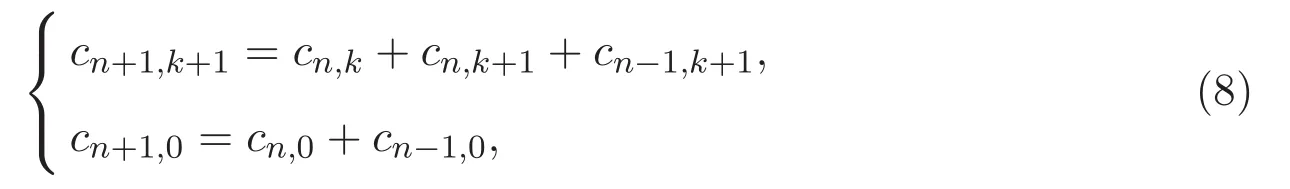
利用引理1.2可得

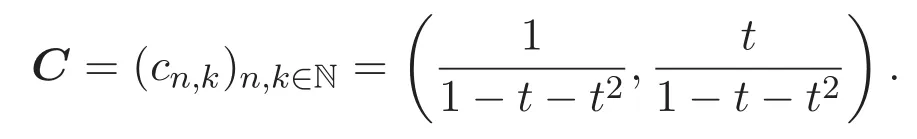
因此可得如下結(jié)果:

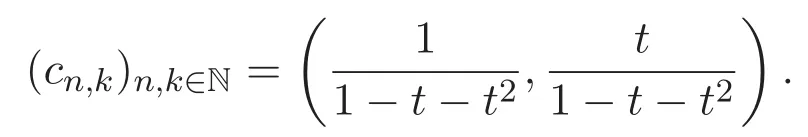
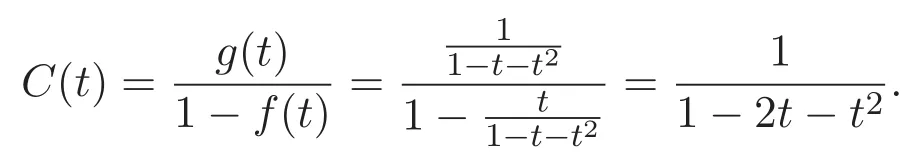
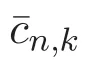
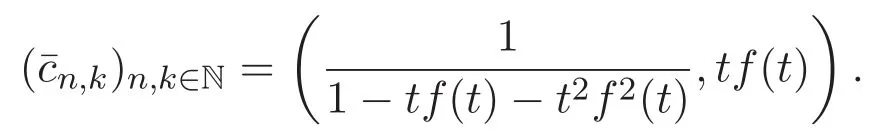
其中f(t)是函數(shù)方程f(t)=1+tf2(t)+t2f3(t)的解.

表2 矩陣的前幾項(xiàng)的值

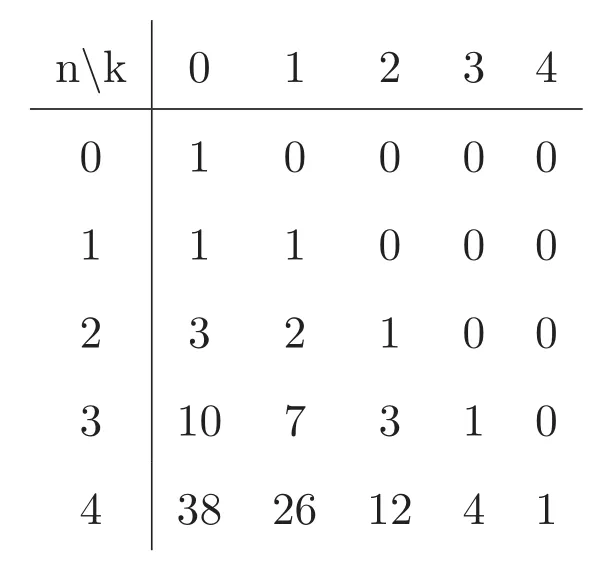
表2 矩陣的前幾項(xiàng)的值

nk 0 1 2 3 4 0 1 0 0 0 0 1 1 1 0 0 0 2 3 2 1 0 0 3 1 0 7 3 1 0 4 3 8 2 6 1 2 4 1

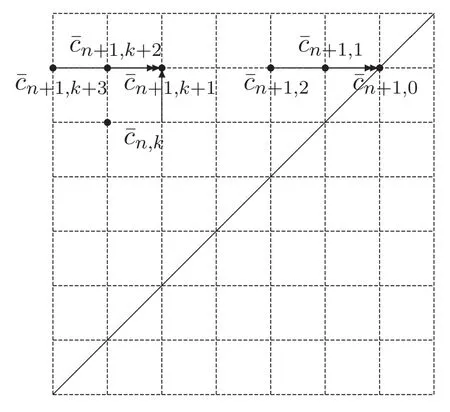
圖2 矩陣的遞推關(guān)系

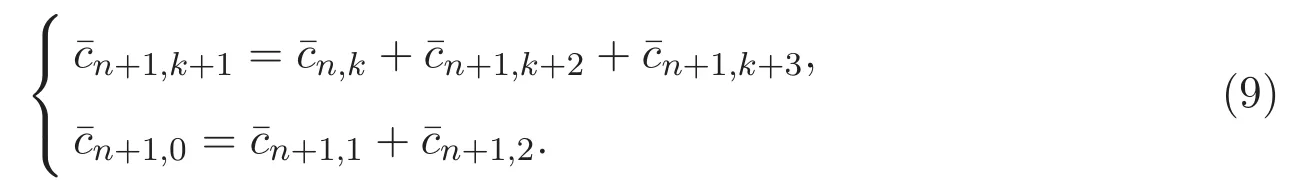
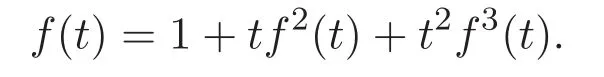
同理可得

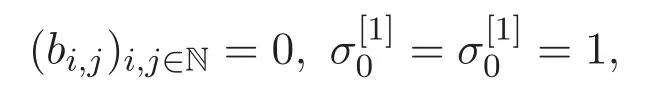
即 R[i](t)=0,S[1](t)=1+t,帶入方程(7)得

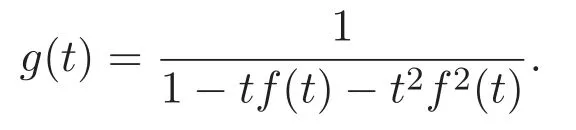
即證

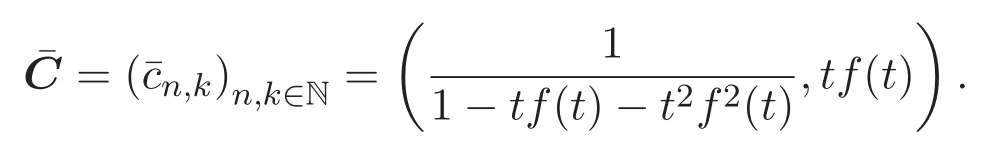
3 Riordan矩陣和廣義的 Pell路

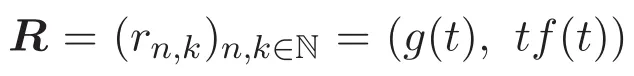
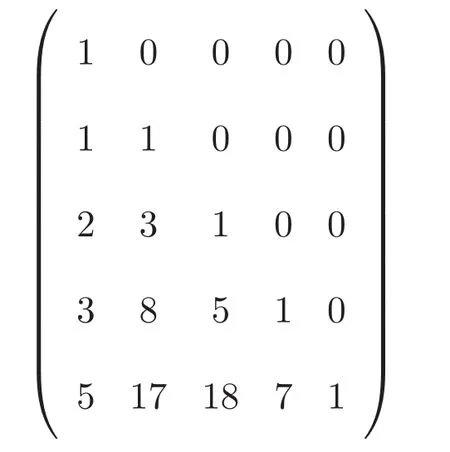
如圖3所示,矩陣R的一般元滿足以下遞推關(guān)系:

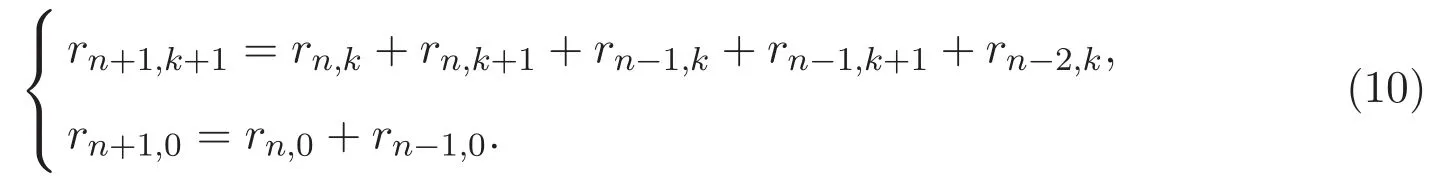
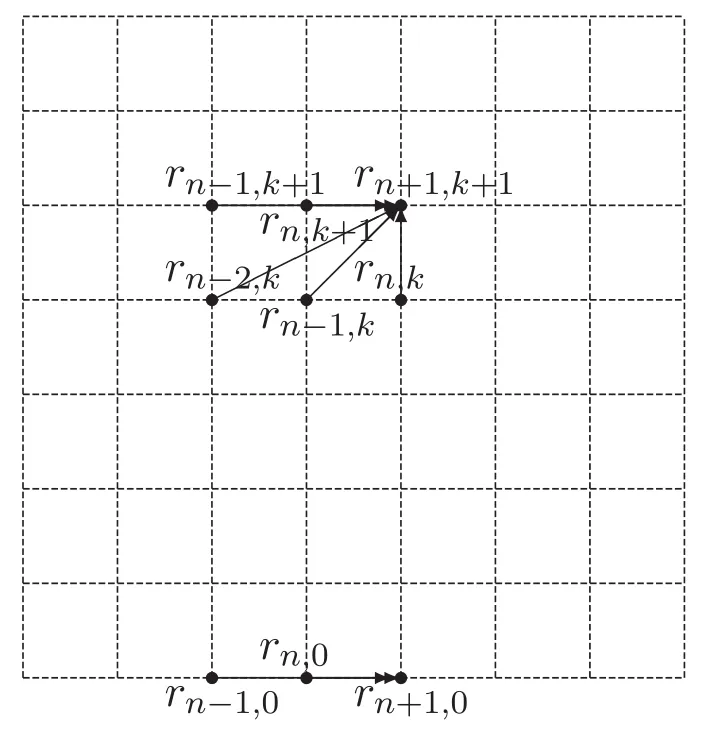
圖3 矩陣R的遞推關(guān)系

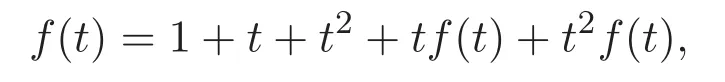
移項(xiàng)合并得

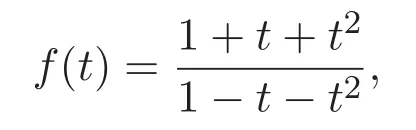
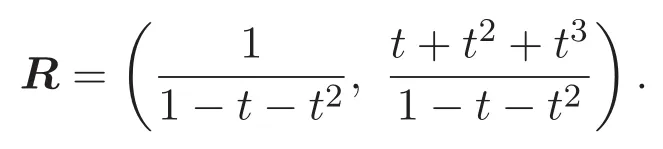
因此可得如下結(jié)果.

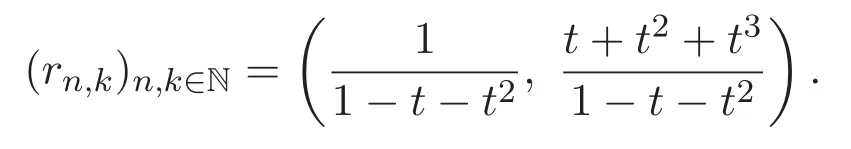
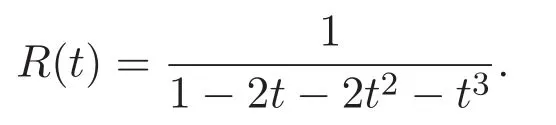
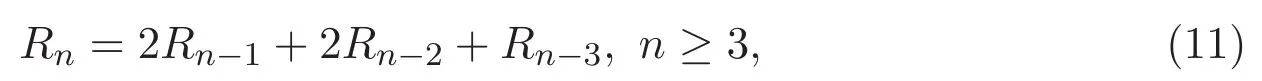
其中R0=1,R1=2,R2=6,序列Rn的前幾項(xiàng)如下:

1,2,6,17,48,136,385,1090,3086,8737,···(見文獻(xiàn) [7]中的序列 A077936).

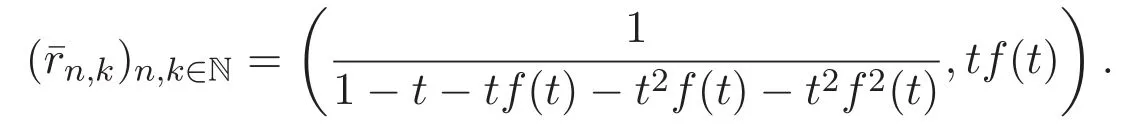
其中f(t)是函數(shù)方程f(t)=1+tf(t)+t2f(t)+tf2(t)+t2f3(t)的解.

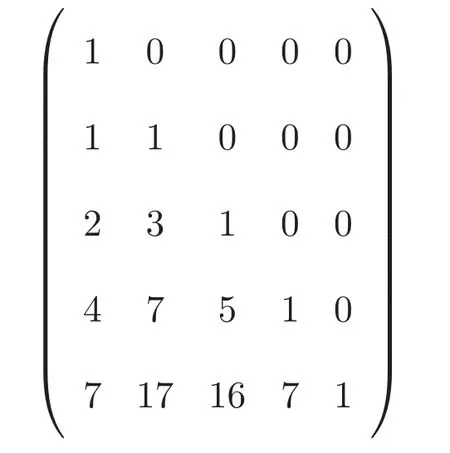
如圖4矩陣S的遞推關(guān)系如下:

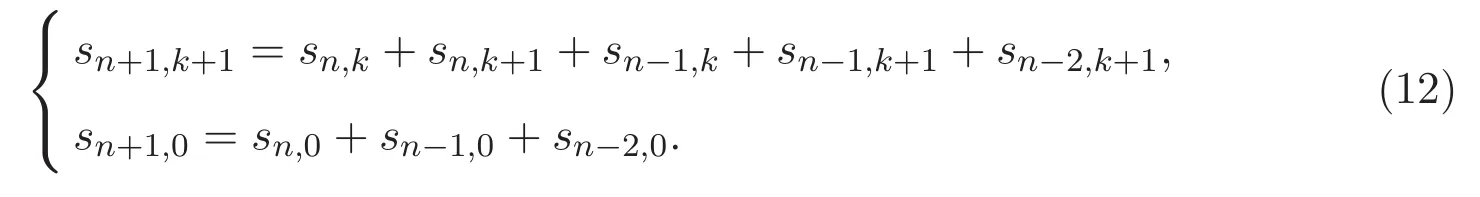
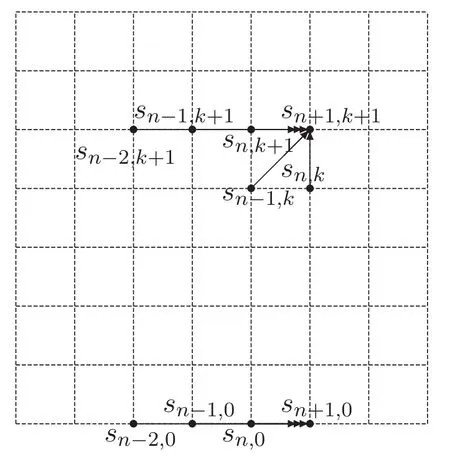
圖4 矩陣S的遞推關(guān)系

利用引理1.2可以得到矩陣S的形式如下:

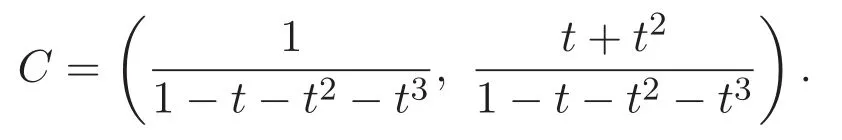
因此可得如下結(jié)果.

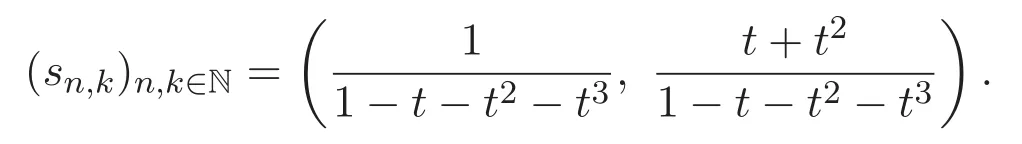
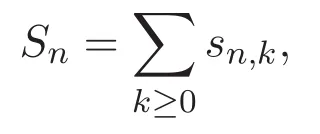
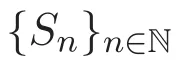
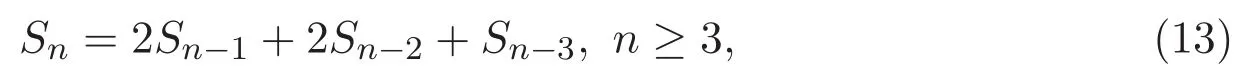
其中S0=1,S1=2,S2=6,序列Sn的前幾項(xiàng)如下:

1,2,6,17,48,136,385,1090,3086,8737,···(見文獻(xiàn) [7]中的序列 A077936).

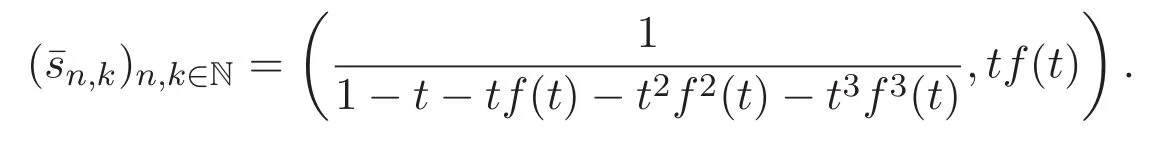
其中f(t)是函數(shù)方程f(t)=1+tf(t)+tf2(t)+t2f3(t)+t3f4(t)的解.