Qin Wu(吳琴)

School of Biomedical Engineering,Guangdong Medical University,Dongguan 523808,China

Keywords: ponderomotive squeezing light,optomechanical system,coupled resonators

1. Introduction

The optomechanical system has sparkled the interest of a vast scientific community due to its distinct applications, ranging from sensing of masses, forces, and displacements at the ultimate quantum limits to tests of the validity of quantum mechanics at a macroscopic level, up to the realization of quantum interfaces for quantum information networks.[1–6]In a typical optomechanical system,a movable mirror couples the cavity field by the radiation pressure, and this coupling can lead to many remarkable effects, for example,the optomechanically induced transparency(OMIT),[7–13]the quantum ground state cooling of the nanomechanical resonators,[14–17]entanglement between cavity modes and/or mechanical modes,[18–25]and squeezed states of the light or the mechanical modes.[26–34]

On the other hand, the squeezed light, with quantum fluctuations below the level of vacuum noise or the standard quantum limit, is particularly useful for ultra-sensitive force measurements,[35]gravitational wave detection,[36]and is also an important resource in quantum information science for continuous-variable information processing.[37]Over twenty years ago,an optomechanical cavity was proposed to generate the so-called ponderomotive squeezing of light[38,39]due to its similarity to a Kerr nonlinear medium. The mechanical element is shifted by the radiation pressure,proportionally to the intracavity intensity of optical field, which in turn modulates the phase of light leading to the correlations between the amplitude and phase quadratures of light. Therefore the optomechanical system behaves similarly to a cavity filled with a nonlinear Kerr medium. It is known that when a cavity containing a Kerr medium is driven by an intense laser,one can obtain appreciable squeezing in the spectrum of quadrature fluctuations at the cavity output. The above analogy therefore suggests that a strongly driven optomechanical cavity will also be able to produce quadrature squeezing at its output. So far,various schemes have been put forward for generating squeezed states either in the light[40,41]or the mechanical system[42,43]and,quite recently, squeezing of the optical field has been experimentally realized in optomechanical systems.[44–47]Experimental realization of the squeezed states is also extended to create and stabilize entangled states,[48]which are important for quantum information processing and precision measurements.

In this paper, we demonstrate a tunable two-mode squeezed light observable in a coupled-resonator optomechanical system, where the two resonators are coupled through photon hopping. One cavity is coherently driven by the pump laser field and the other cavity couples to a high-Q mechanical oscillator via radiation pressure. In such a system, the introduction of two coupled resonators owning tunable coupling strength will present distinct features. One of the features is double-optomechanical induced transparency.[49]Here we show the feature of the squeezing spectrum and discuss in detail the dependence of squeezing properties(including optimal squeezing position,squeezing degree and squeezing range)on system parameters, such as the detuning between the cavity and pump laser, the coupling strength between the two resonators,the power of the pump laser,the environment temperature,and the decay of cavity. We find that the single peak in squeezing spectrum turns to two peaks due to the stronger tunneling strength. Compared to previous studies,[50–53]where the ponderomotive squeezing is generated in an optomechanical cavity assisted by an atomic ensemble or two movable mirrors, our scheme owns some favorable features. First, the two-mode squeezed light generated in our scheme is created by the introduction of the two tunneling resonators. In addition, the tunneling strength is tunable by adjusting the positions of the resonators. Second, strong squeezing spectrum with wide squeezing frequency range can be obtained by appropriate choice of parameters present in our optomechanical system. Finally, both the cavity decay and environment temperature play a positive role in generating better pondermotive squeezing light, which means that the squeezing light in our model is more easily to be observed in experiments.

The rest of this paper is organized as follows. In Section 2 we describe the model studied, derive the analytical expressions and the quantum Langevin equations of the optomechanical system. In Section 3, we give explicit relations for the ponderomotive squeezing spectrum of the transmitted field, and discuss the squeezing properties of the system. A conclusion of our findings is given in Section 4.

2. Model and solution

For an optomechancial system consisting of two coupled optical resonator as shown in Fig.1,two cavity fields are coupled via the photon tunneling interaction. The cavity on the left is driven by the pump laser field, and the cavity on the right couples to the motion of oscillator through the radiation pressure. In the rotating frame of pump laser frequency ω0,the Hamilton is given by

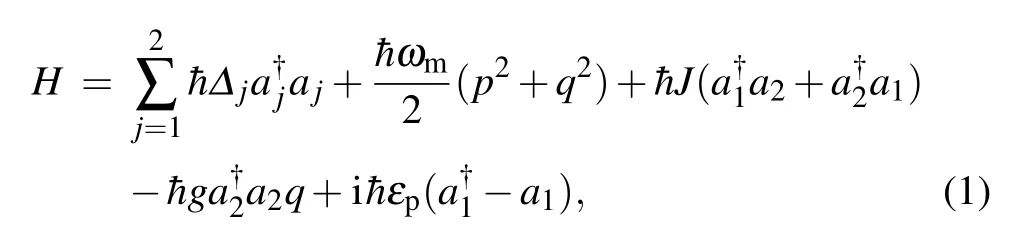
Using the Heisenberg equations of motion and taking into account the corresponding damping and noise terms, we can reach the quantum Langevin equations for the operators of the mechanical and optical modes

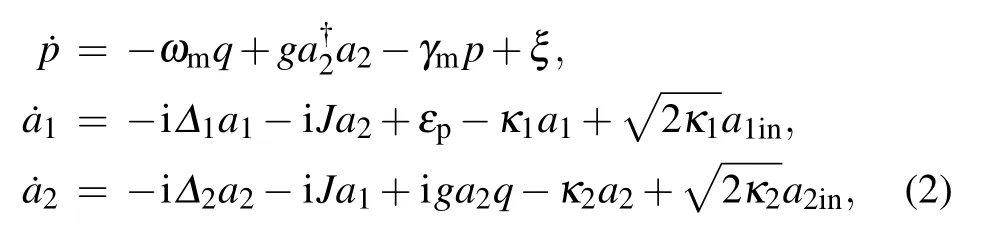
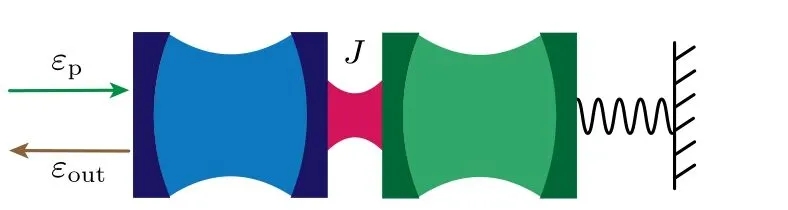
Fig.1. Coupled-resonator optomechanical system consisting of two tunneling-coupled optical cavity modes a1 and a2,and a movable mirror coupled to the mode a2 via radiation pressure. The system is driven by a pump filed εp from the left side with frequency ω0.

We can rewrite each Heisenberg operator as a steady-state value plus an additional fluctuation operator with zero-mean value, aj= ajs+δaj(j = 1,2), q = qs+δq, p = ps+δ p.Then we substitute these expressions into the Langevin equations and obtain the steady-state values

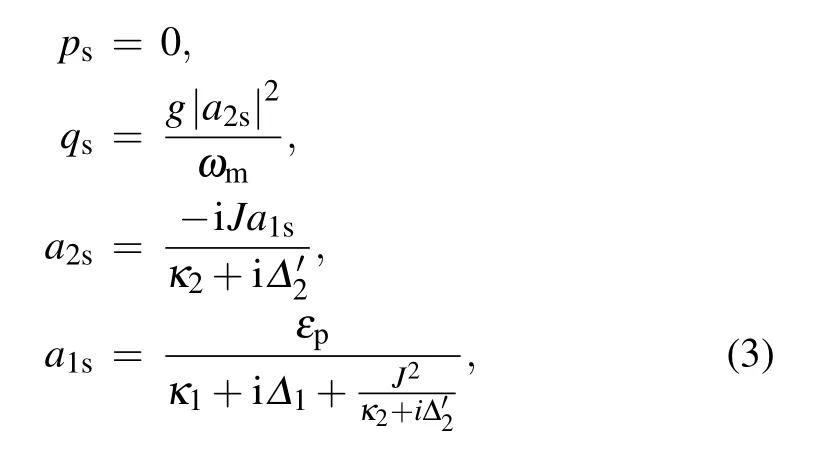
Retaining only first-order terms in the small quantities δo(o = a1,a2,q,p), the linearized Langevin equations are given as follows:

where G0=ga2sis the effective coupling strength.

It is more convenient to work in the frequency domain because, experimentally, fluctuations of the electric field are more convenient to be measured in the frequency domain than in the time domain. For calculation in frequency domain, we introduce the Fourier transform for an operator u(u=δa1, δa2, δq, δ p, a1in, a2in,ξ)as

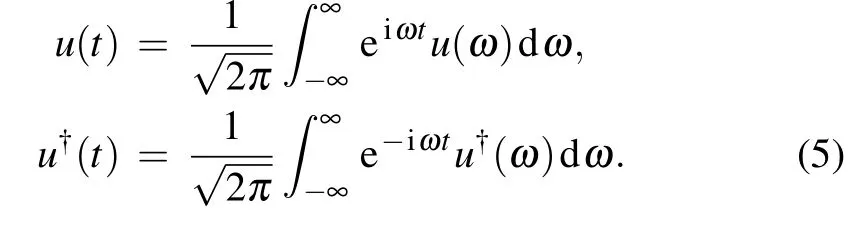
Then we rewrite Eqs.(4)in the frequency domain as

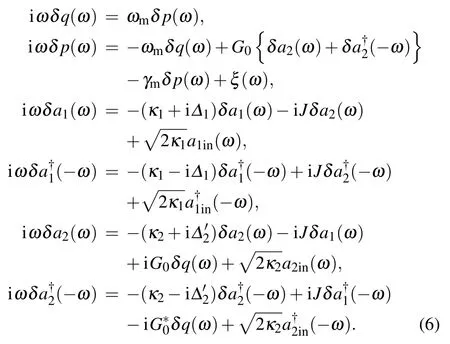
By solving the above equations,we obtain

where the coefficients are given as follows:

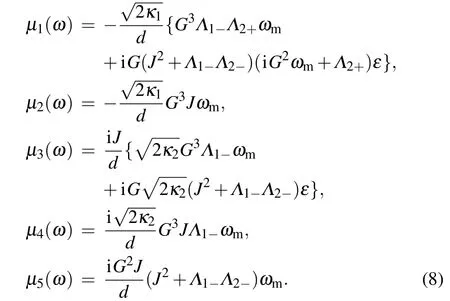
Here we have defined

In the following, we will study the ponderomotive squeezing numerically in the frequency domain.

3. Ponderomotive squeezing

It was shown that the optomechanical coupling can lead to squeezing of the nanomechanical motion, which can be inferred by measuring the squeezing of the transmitted microwave field.Here we analyze the squeezing properties of the transmitted field,which is accessible to experiment and useful for practical applications.[44–46]The squeezing spectrum of the transmitted field is given by[39]

Using the results of Eq.(7),and the following correlation functions in the frequency domain:

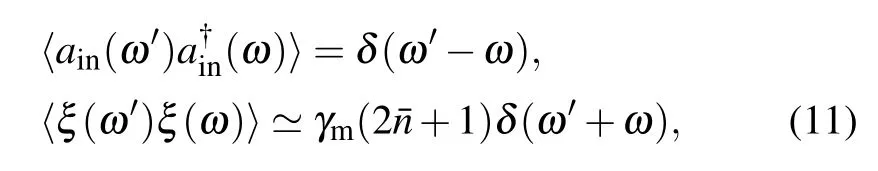
we can obtain

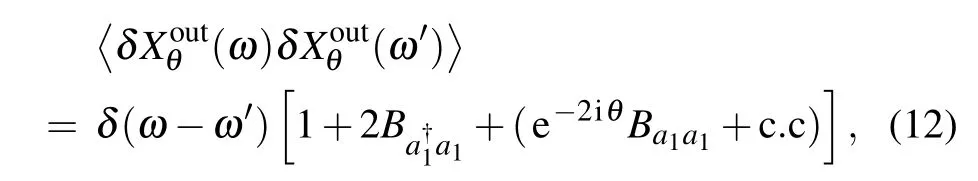
where

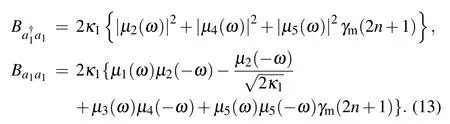
Substituting Eq.(12)into Eq.(10)yields the squeezing spectrum in a simple form

As the phase angle θ is an adjustable parameter, we choose appropriate θ by solving dSθ(ω)/dθ =0,then we obtain

Here, we choose the negative value to optimize the degree of squeezing. Thus the squeezing spectrum can be rewritten as

Now we turn to discuss the feasibility of the squeezing spectrum in the coupled-resonator optomechanical system,and the relationship of the squeezing properties to the system parameters, such as the detunings between cavities and the pump laser, the tunneling strength of the two resonators, the power of pump laser,the environment temperature,and decay rate of the cavity. For simplicity, we assume that two cavity fields have the same decay rate,i.e.,κ1=κ2=κ. To demonstrate the numerical results, we use the experimentally realizable parameters:[54,55]λc=1064 nm, ωm=2π×107Hz,γm=628 Hz,L=1 mm,m=12 ng.

Fig.2. The squeezing spectrum with different detunings between the cavities and the pump laser when T =15 mK, P=10 mW, J =κ =0.5ωm: (a) ?1 = =ωm; (b) ?1 =?ωm, =ωm; (c) ?1 =ωm,=?ωm;(d)?1==?ωm.

With the enhancement of the tunneling strength of the two resonators, two peaks appear in the transmitted field, which can be easily seen from Fig.3. This is due to the fact that an additional hybrid energy level is effectively introduced into the original three-level system by the stronger tunneling coupling between the optomechanical resonator and the left resonator. It is worth mentioning that our proposal is quite different from the previous idea,[51,52]where two-mode squeezed light is caused by the frequency difference between the two movable mirrors[51]or the Coulomb coupling between the two movable mirrors.[52]The introduction of tunneling coupling between the two resonators also leads to a split in the OMIT window, as reported in Ref.[49]. Comparing the four curves in Fig.3,we can find that the degree of squeezing at the point ω ?±ωmincreases and the point where the maximal squeezing occurs shifts slightly to the right side with the tunneling strength between the two resonators.

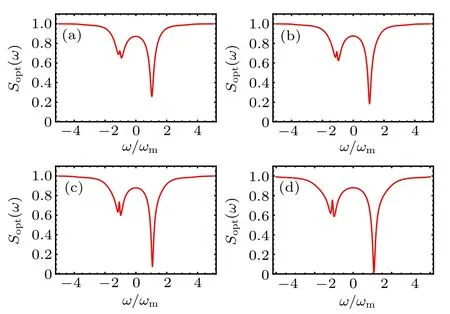
Fig.3. The squeezing spectrum with different tunneling strength J of two resonators when T =15 mK,P=10 mW,κ =0.5ωm,?1=?′2=ωm: (a)J=2.3ωm;(b)J=2.5ωm;(c)J=2.7ωm;(d)J=2.8ωm.

Then we show the effect of the pump laser power on the squeezing spectrum in Fig.4. It can be easily seen that the maximal squeezing degree remains unchanged with the increase of the pump laser power. However, the spectral range of the squeezed light becomes wider and wider by increasing the power of the pump laser. The half height width of the squeezing spectrum at frequency ω ?ωmis about 0.35ωmin the case of P=10 mW (Fig.4(a)). With the increase of the pump laser power,the half height width of the squeezing spectrum at frequency ω ?ωmchanges to 0.9ωm(P=40 mW),1.4ωm(P=80 mW),and 2.1ωm(P=200 mW),which means that the frequency range of squeezing becomes wider with the increase of pump laser power. Especially, the frequency range of squeezing is about ?5 ≤ω/ωm≤5 in the case of P=200 mW. This is due to the fact that a larger power will input amount photons which will effectively overcome the effects of thermal noise.

The robustness of squeezing dependent on the environment temperature T is shown in Fig.5. Here we choose the power of pump laser is 1 mW and the other parameters are same as those used for Fig.3. Figure 5 displays perfect two-mode squeezing spectrum at frequencies ω =±ωmwith different squeezing degree. In the case of T =15 mK and T =55 mK,the squeezing degree at ω=?ωmis smaller than that at ω =ωm. However,the squeezing degree at ω =?ωmis larger than that at ω =ωmin the case of T =225 mK,and the squeezing degrees at these two points ω =±ωmare equal to each other in the case of T =125 mK.In other words, the squeezing degree at ω=?ωmincreases with the temperature,while the squeezing degree at ω=ωmdecreases with the temperature.

Fig.4. The squeezing spectrum with different power of pump laser when T =15 mK,J=2.3ωm,κ=0.7ωm,?1=?′2=ωm:(a)P=10 mW;(b)P=40 mW;(c)P=80 mW;(d)P=200 mW.

Fig.5. The squeezing spectrum at different temperatures when P=1 mW, J =2.3ωm, κ =0.5ωm, ?1 ==ωm: (a) T =15 mK; (b)T =55 mK;(c)T =125 mK;(d)T =225 mK.

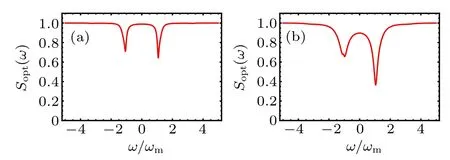
Fig.6. The squeezing spectrum with different cavity decay rates of the cavities when T =15 mK,P=10 mW,J=2.3ωm,?1==ωm: (a)κ =0.1ωm;(b)κ =0.4ωm.

Finally, we show the squeezing spectrum with different decay rate κ of the cavities in Fig.6. Comparing Fig.6(a)(κ=0.1ωm),Fig.6(b)(κ=0.4ωm)and Fig.4(a)(κ=0.7ωm),we can find that not only the squeezing degree is enhanced but also the squeezing range is widened with the decay of the cavity. This indicates the squeezing robustness with respect to the decay of the cavity. The optimal squeezed light can be even observable in the bad cavities. Therefore, the squeezed light spectrum in our model is easy to be achieved experimentally.

4. Conclusion

We have analyzed the properties of the ponderomotive squeezed light observable in an optomechanical system with two coupled resonators. We show that a two-mode tunable squeezed light can be achievable in this system due to the large tunneling strength between the two resonators. In the case of small tunneling strength where the squeezing spectrum presents only a single peak,the squeezing orientation is influenced by the detuning between the left cavity and the pump laser. We also find that the squeezing degree can be flexibly controlled by adjusting the tunneling strength, the decay of the cavities and the environment temperature. Especially, the larger the cavity dissipation,the higher the squeezing degree.In addition, the frequency range of squeezing becomes wider with the increase of laser power and cavity decay. In other words, even the cavity dissipation and environment temperature play a positive role in the generation of good squeezing light. Thus,the squeezed light spectrum in our model is easy to be observed experimentally.

Acknowledgment

We thank Henan Key Laboratory of Electromagnetic Transformation and Detection for the support.