(Hiwing Satellite Operation Division of China Aerospace Science and Industry Corporation,Bejing 100070,China)

Abstract: The design of random media access control (MAC) protocol has been attracting great attention for satellite communication networks,where the propagation delay is long and the traffic load is varying.Advanced coded random access schemes tend to provide resource allocation strategies for massive uncoordinated devices,where multiple packet replicas from each user are transmitted in random slots of the frame and successive interference cancellation (SIC) iterations are tracked to recover collided packets at the receiver.It is assumed that each active user just has a single information packet to be transmitted.In this paper,an MAC layer random access scheme named Multi-Packets Transmitted Irregular Repetition Slotted Aloha (M-IRSA) is proposed.Different from the existing advanced random access schemes,the M-IRSA scheme supports various number of packet transmission per user by using pre-coding procedure.Joint decoding combined with SIC iterations and local decoding is analyzed.The simulation results show that the proposed scheme is more efficient compared with the IRSA scheme without packet loss rate(PLR)loss.

Keywords:Aloha; coded random access; MAC; satellite network; successive interference cancellation

1 Introduction

Recent years have witnessed the explosion of wireless machine-type communications (MTC) in satellite networks.Typical MTC networks involve a massive set of battery-powered or harvesting-powered devices autonomously transmitting small data,i.e.,short messages.Current multiple access control (MAC) layer solutions for MTC networks tend to privilege scheduled and coordinated transmissions,in compliance with the classical information-theoretic assumptions[1].Traditionally,the coordinated multiple access schemes can take efficient usage of the available bandwidth.However,it requires control signaling that may even outnumber data[2],which is particularly challenging.Opposed to coordinated schemes,random access schemes provide a common channel to be dynamically and opportunistically shared by a population of users without coordination requirements.

As a practical and effective solution to massive uncoordinated multiple access,coded random access has been the subject of several investigations in the past few years,combining user packet replication (or packet coding) with successive interference cancellation (SIC) at the receiver.The Collision Resolution Diversity Slotted Aloha (CRDSA) protocol[3]was the first scheme to exploit SIC to resolve collisions on a random access channel,where the users repeat their transmission twice in a frame.The Irregular Repetition Slotted Aloha (IRSA) was introduced in Ref.[4] to provide a further throughput gain over CRDSA,by optimizing the transmission repetition rate for each packet.An extension of IRSA access strategy named Dubbed Coded Slotted Aloha was proposed in Ref.[5],where the packets are encoded prior to transmission in the MAC frame,instead of being simply repeated.Since then,coded random access emerging as a new paradigm has been the subject of several investigations[6-10].With this paradigm,the throughput is substantially increased,which makes it a practical and efficient solution to support for uncoordinated access.In the coded random access schemes,each information packet is repeated mutiple times and transmitted over time slots.However,compared with the Aloha schemes,they require more energy for transmission.Furthermore,in the coded random access schemes mentioned above,each user is able to transmit only one packet per frame even the user has multiple packets to transmit.

As a potential application,users acting as relays in a cellular network have various number of packets to transmit per frame; the sizes of data are different according to the types of platforms.Reservation-CRDSA (R-CRDSA) with access control[11]was designed for the case in which the user has multiple fragmented packets to transmit.A specific slot of each frame is reserved for the user until the end of the last packet.Without SIC,collisions cannot be cancelled in unreserved slots,leading to low throughput performance.The Multiple Reservation-CRDSA (MR-CRDSA)[12]scheme was developed based on the R-CRDSA scheme,where multiple slots are reserved under low traffic loads.The users with one information packet will have no opportunities to access the channel if all of the slots are reserved,which is not practical in communication systems.

We investigate the application where users who have various number of packets to transmit per frame and propose a scheme named Multi-Packets Transmitted Irregular Repetition Slotted Aloha (M-IRSA),where no load control mechanism or load estimation procedure is needed.Multiple information packets from the same user are pre-coded before transmission.The decoding method is a joint one that combines SIC iterations and local decoding procedure.The proposed scheme promises higher efficiency without packet loss.

2 IRSA Scheme and SIC Procedure

In IRSA schemes,the repetition rate of each user is optimized compared with that in the CRDSA schemes.Each user sends several replicas according to a probability distribution instead of two replicas in CRDSA.The IRSA scheme and SIC procedure is shown in Fig.1.

In Fig.1a,useru1has three replica packets (u1.1,u1.2andu1.3),all of them having the same information data.The SIC iterative procedure in IRSA is similar with the decoding process for LDPC codes over the erasure channel,which is represented by the bipartite graph (Fig.1b).In each replica,the information about the position of other replicas is included,e.g.in a dedicated header field.If one packet replica is recovered,the positions and the content of the other replicas will be known.This way,the interference of this packet can be canceled.For example,u1.2andu1.3can be recovered by the receiver as the interference ofu1.1is removed.

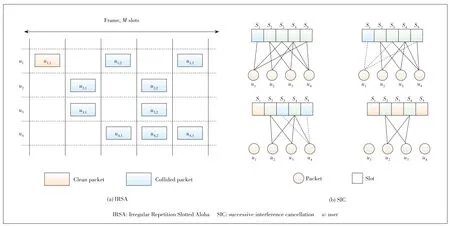
▲Figure 1.IRSA scheme and SIC procedure.

The traffic loadGrepresents the average number of information packets per slot.The threshold is defined as the maximum value ofGthat the bursts shall be recovered with a probability close to 1.WhenGis above the threshold,the SIC procedure will fail and the packet loss rate (PLR) shall increase.The threshold can be calculated by“and-or”tree.

The IRSA scheme promises quite a remarkable throughput.However,two of its characteristics should be considered.First,IRSA has lower critical points compared to the slotted Aloha.When the offered load increases above a critical point,the throughput will decrease rapidly; in other words,the critical point is the offered load level,where the maximum throughput is attained.Second,each user in an IRSA system performs a single transmission within each MAC frame.When the number of users is low while they have a lot of packets to transmit,the channel resources cannot be used efficiently.

3 Proposed M-IRSA Scheme

3.1 System Model

The M-IRSA framework is inspired in the situation where a large number of un-cooperated users are seeking access to a receiver.A slotted and framed random access system is considered at the MAC layer,where each frame is divided intoMtime slots.The users form a population sizeUand attempt transmission at the beginning of a new frame.It is assumed that thei-th user haski(ki≥0) information packets to be transmitted.(Thei-th user has no packet to transmit ifki=0.)Accordingly,the total number of information packets to be transmitted is.The number of information packets to be transmitted is random and independent with each other,so the total number of information packetsNis unknown to the receiver.We define a parameterDito present the normalized information packet data size of thei-th user,which is given byDi=ki/M.

The normalized traffic loadGis given by,which represents the average number of information packet transmission per slot.

In this paper,a classical MAC collision channel model is used.The packet loss is only caused by collisions,which means the collided packets can be recovered if the interference from other packets is removed.This assumption is reasonable since the bursts have been encoded via the (4096,1992) concatenated extended Bose-Chaudhuri-Hocquenghem(BCH) structured irregular repeat accumulate (S-IRA) code and transmitted with quadrature phase shift keying (QPSK)modulation.The results atEb/N0=2 dB confirm that the performance degradation with the actual IC algorithm is negligible in both the low and the high PLR regions.

3.2 Operation of M-IRSA

For thei-th user,kiinformation packets are pre-coded via linear block coding before transmission.The coded packets are transmitted to the receiver.

A zero (M,ki) generating matrix is initialized,where theMrows denote the positions of slots and thekicolumns represent information packets.The coding degree of information packets follows a given distribution {Λl},where Λldenotes the probability of an information packet choosinglpositions out ofMrows randomly.Thei-th user sends the output coded packets to the corresponding slots respectively.The indexes of information packets and their corresponding positions are included in the header of output coded packets.In practical implementations,the overhead due to the inclusion of pointers in the header of the coded packet may be reduced by adopting more efficient techniques.A more elegant approach to address this issue is to embed in each coded packet the number of information packets and a user-specific seed of a pseudorandom generator known both to the user and the receiver.Once a coded packet is resolved,the receiver can use the knowledge of the generator and the obtained seed to determine the generation matrix.Since the positions are selected randomly,it happens that some positions are not chosen by the information packets.The actual number of coded packets is denoted byhi(hi≤M).We define the pre-coding rate of thei-th user asRi=ki/hi.

It is assumed that each user has one buffer.Before transmitted,the information packets are preserved in the buffers.Therefore,it is possible that the users are aware of the number of information packets.The information packets are pre-coded via linear block coding before transmission.The generating matrix is random.But the maximum length of coded packets is fixed,which is equal to the frame length.

(1)Example 1.

As shown in Fig.2,there are 2 active users,where the useru1contains 3 information packets (circles),by an index{k1,1,k1,2,k1,3},and the useru2contains 2 information packets(circles),by an index{k2,1,k2,2}.The first information packet ofk1,1selects positionS1andS3; the information packetk1,2selects positionS2,S3andS5; the information packetk1,3selects positionS1andS4.Thus,the generating matrix ofu1is

In the same way,the generation matrix ofu2is

The useru1generates 5 coded packets,by an information index{h1,1,...,h1,5},and transmits them toS1,S2,S3,S4andS5.The useru2generates 3 coded packets,by an information index{h2,1,...,h2,3},and transmits them toS1,S2andS6.The precoding rates of the two users areR1=3/5 andR2=2/3.

▲Figure 2.An Multi-Packets Transmitted Irregular Repetition Slotted Aloha(M-IRSA)example with frame size m= 6 slots and 2 active users.The first user u1 contains 3 information packets and generates 5 coded packets.The user u2 contains 2 information packets and generates 3 coded packets.Slots s1 and s2 suffer from collisions.

At the receiver,singleton slots are the ones with only one coded packet transmitted to each slot.A collision takes place in a slot when two or more coded packets are simultaneously transmitted to the slot.Such a slot is called collision slot.In the meanwhile,once a collision is detected,no more information about the number and content of colliding packets can be achieved by the receiver.The decoding procedure at the receiver combines SIC iterations and local decoding procedure.It is conducted iteratively as follows until all of the information packets are recovered or collisions persist with no further information packets being recovered.As seen in Fig.2,S1andS2are collision slots,whileS3,S4,S5andS6are singleton slots.

·Round 1(SIC procedure):Coded packetsh1,3,h1,4,h1,5andh2,3are known by the receiver,asS3,S4,S5andS6are singleton slots.It also means thatk1,1⊕k1,2,k1,3,k1,2andk2,1⊕k2,2are known by the receiver.Once a coded packet is received by the receiver,the generating packets will be cracked.

·Round 1(local decoding procedure):The information packetsk1,1,k1,2,andk1,3will be recovered based on the knowledge ofk1,1⊕k1,2,k1,3andk1,2.Then the coded packetsh1,1(k1,1⊕k1,3)andh1,2(k1,2)will be known by the receiver.

· Round 2 (SIC procedure):The contributions of interference due toh1,1andh1,2are canceled respectively,makingS1andS2new singleton slots.Coded packetsh2,1andh2,2will be known by the receiver.

·Round 2(local decoding procedure):The generating packets ofu2are cracked during round 1(SIC procedure).Then the information packetsk2,1andk2,2will be recovered based on the knowledge ofh2,1andk2,2.

(2)Example 2.

As seen in Fig.2,S1andS2are collision slots,whileS3,S4,S5andS6are singleton slots.Coded packetsh1,3,h1,4,h1,5andh2,3are recovered asS3,S4,S5andS6are singleton slots (Step 1).Then the correctly recovered coded packets help to recover the information packets,making information packetsk1,1,k1,2andk1,3recovered.Hence,the coded packetsh1,1andh1,2are known by the receiver (Step 2).Next,the contributions of interference due toh1,1andh1,2are canceled respectively,makingS1andS2new singleton slots (Step 3).A second decoding iteration is then triggered.

4 Performance Analysis

4.1 Pre-Coding Rate

In the pre-coding procedure,the information packets'degree distribution is given by,whileis denoted as the average packet repetition rate.On the other side,the position's degree distribution tends to be the Binomial distribution,which is expressed as.The average number of information packets per position is.It is easy to verify that the probability that a generic user sends an information packet within a given position is

The probability that one coded packet haslinformation packets is given by

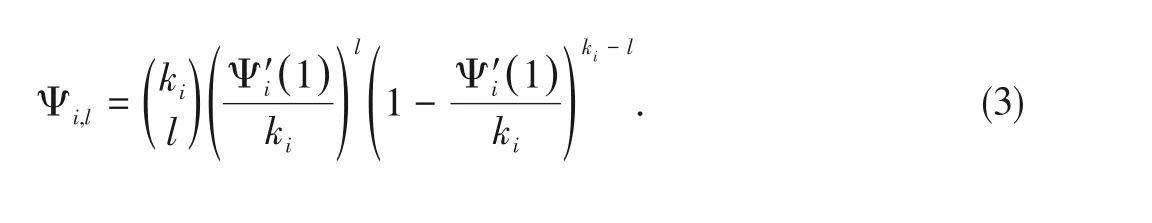
Mi,Iis defined as the expected number of positions with no information packets,which is given by

It is assumed that information packetskiare generated by coded packetshiand sent to time slotshiby the userui.Obviously,we havehi≥ki.The expected length of coded packets is E[hi]=max(ki,M-Mi,I).Hence,the expected rate ofRiis

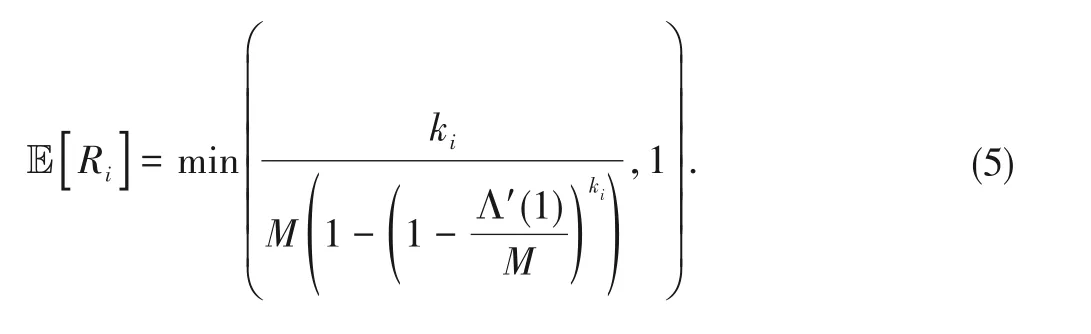
In the IRSA scheme,each user has only one information packet to transmit,which meanski=1.According to Eq.(5),we have the expected coding rate of the IRSA scheme as:

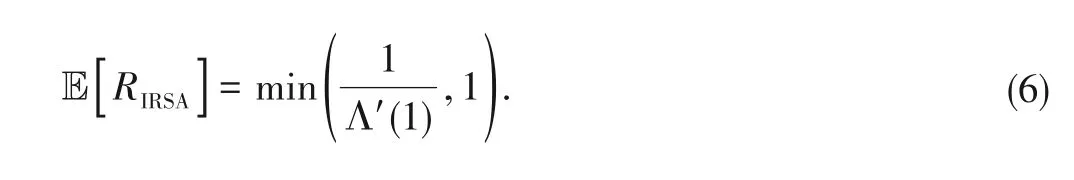
It should be noted that the proposed M-IRSA scheme becomes a typical IRSA scheme when each user only has one information packet to transmit.The pre-coding rate turns to be 1/Λ'(1).

Moreover,the approach is actually peer-to-peer transmission when there is only one active user.The maximum precoding rate 1 can be achieved as there is no interference from other users.

4.2 Packet Loss Rate and Throughput

We analyze the evolution of the interference subtraction in the proposed scheme in the asymptotic case whereNtends to infinity.In the“AND-OR”tree,each OR node evaluates logical OR operation on the value of its children and each AND node evaluates logical AND operation on the value of its children.One edge of the OR node is revealed once one of the other edges connected to the node has been revealed; on the contrary,one edge of the AND node is revealed whenever all the other edges connected to the node have been revealed.In the proposed multiple access scheme,information packets act like the OR nodes; time slots act like the AND nodes; coded packets act like the OR nodes in SIC iterations and act like the AND nodes in local decoding procedure.

We define thatqis the probability that an edge of information packet is unknown,tis the probability that an edge of coded packets connected to one information packet is unknown,?is the probability that an edge of coded packets connected to one time slot is unknown,andpis the probability that an edge of one time slot is unknown.

Now the edges between information packets and coded packets are considered,withλldenoting the probability that an edge is connected to an information packet of degreelandρldenoting the probability that an edge is connected to a coded packet of degreel.They can be expressed byλl=

It is supposed that there are two active users (u1andu2) in the system,whereu1hask1information packets generated toh1coded packets andu2hask2information packets generated toh2coded packets.After transmission,some coded packets are collided.It is assumed that (1-?1)h1out ofh1coded packets and(1-?2)h2out ofh2coded packets are received by the receiver without collisions.It is easy to verify that the number of collision slots is?1h1=?2h2.All of the information packets have the same edge degree distributionλl,whileρ1,landρ2,lare the coded packets'edge degree distribution ofu1andu2respectively.

One edge connected to one information packet is unknown when all of the other edges connected to the same information packet are unknown.One edge connected to one un-collided(un-erased) coded packet can be known when all of the other edges connected to the same coded packet are known.The edges connected to collided (erased) coded packets do not transfer information during the local decoding procedure.Therefore,during thej-th iteration,for the useru1,we have

The recovery of information packets may help to recover the collided (erased) coded packets.One collided (erased) coded packet turns to be known when all of the connected edges from information packets to the coded packets are known.?1is the probability that an edge of coded packet connected to one slot is unknown,which can be expressed as

In the same way,for the useru2,we have

4.2.2 SIC Procedure

The recovery of collided (erased) coded packets then helps the implementation of the SIC procedure.New clean slots appear since the interference from the recovered coded packet is canceled.Hence,the collision (erasure) probability is updated.One edge connected to a collided time slot is known only when the other edge connected to the same slot is known.Therefore,we have 1-?1,j=1-?2,j-1and 1-?2,j=1-?1,j-1.

The local decoding procedure and the SIC procedure implement iteratively.According to the equations above,we get the expressions ofqandtas follows.

I went back to the nurses station and mentioned we had a homeless family in the waiting room-a mother and four children between four and ten years of age. The nurses, grumbling about working Christmas, turned to compassion12 for a family just trying to get warm on Christmas. The team went into action, much as we do when there s a medical emergency. But this one was a Christmas emergency.

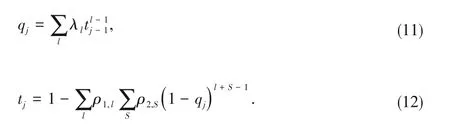
By lettingN→∞(k1→∞;k2→∞),the coded packets'degree distribution follows a Poisson distribution.For the useru1,we have

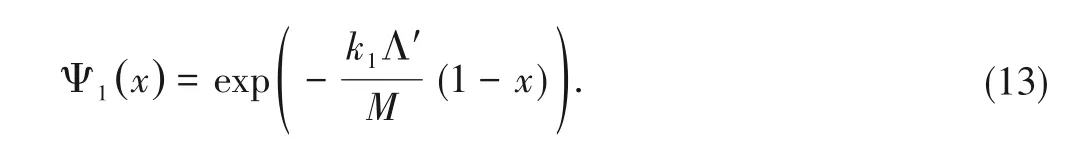
The polynomial representation of edge degree distribution of coded packets is

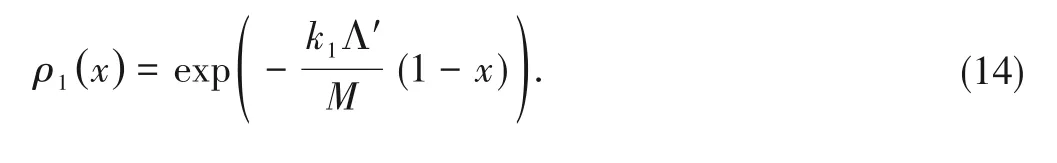
Similarly,foru1andu2,we have

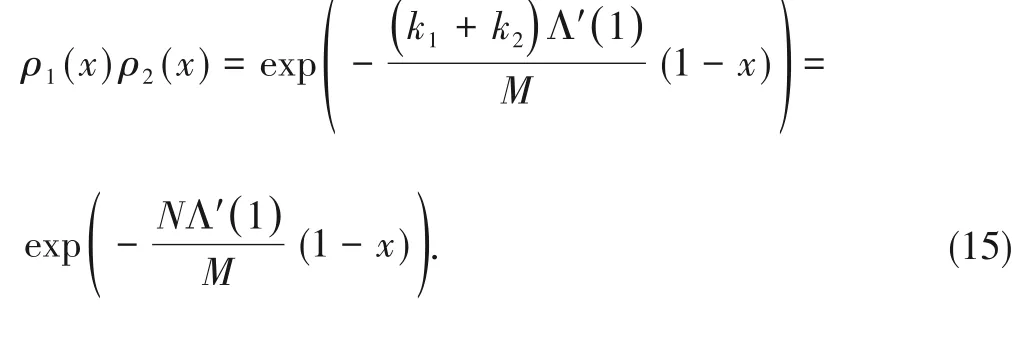
The evolution iteration after the iteration of the probabilityqis given by

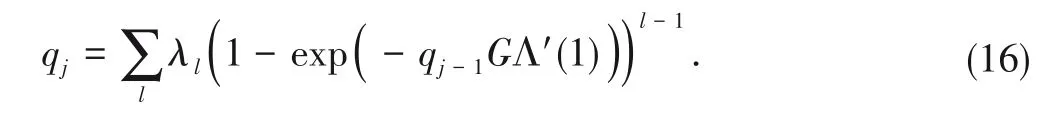
The theoretical analysis of the M-IRSA scheme can be extended to multiple users (more than two users),which is verified in the next section by numerical results.According to Ref.[4],the probabilityqin the proposed M-IRSA scheme has the same expression with that in the IRSA scheme.

The normalized throughputTis defined as the probability of successful information packet transmission per slot,which is given by.In this way,PLR can reflect the performance of throughput.

5 Simulation Results

In this section,numerical results are illustrated.We consider an MAC frame sizeM=200 slots and a user population sizenpop=200.There are two kinds of users in the simulation:each of 100 out ofnpopusers has 2 information packets to transmit once each of the other 100 users has 5 information packets to transmit once activated.Each user becomes active at the beginning of any frame with probabilityp,independent of the other users and regardless of the user's activation history.The repetition rate of each user is following the distribution Λ(x)=0.5x2+0.28x3+0.22x8.

Fig.3 shows the expected pre-coding rate versus the normalized packet data size.The x-axis represents the average normalized information packet data size of the users.The y-axis represents the average pre-coding rate.In a typical IRSA scheme,each information packet is transmitted repeatedly with a given distribution,so the pre-coding rate is constant versus the normalized packet data size and only rates 0 ＜R＜12 can be obtained.As shown in the figure,the expected coding rate of the IRSA scheme is E[RIRSA]=1/0.5× 2 +0.28× 3+0.22 × 8,which means the users are expected to transmit 3.6 coded packets for one information packet.On the other hand,the expected coding rate of the M-IRSA scheme is varied according toDi(the normalized information packet data size of the user).It needs less coded packets for one information packet,which means the proposed M-IRSA scheme is more effective than the IRSA scheme especially with large normalized packet data size in the pre-coding procedure.

Figs.4 and 5 show the PLR and throughput performance comparison of the proposed scheme and typical IRSA scheme when the traffic loadGis fixed.It can be seen that the proposed scheme is more effective without PLR.

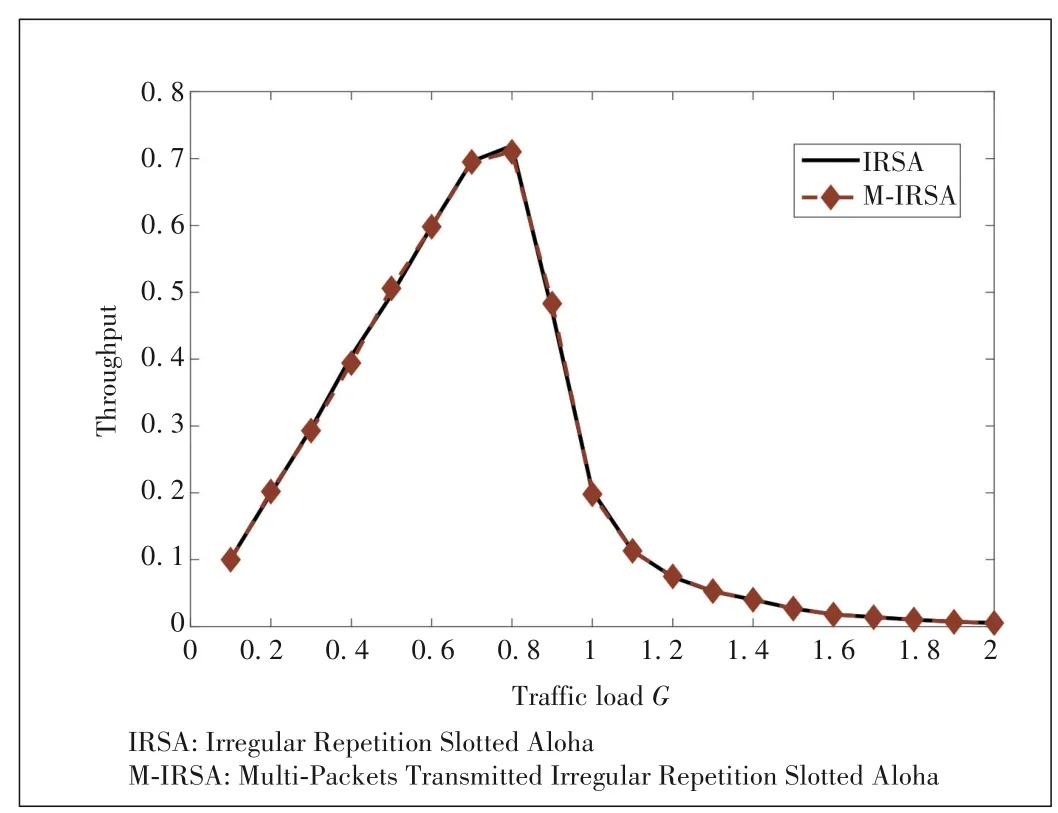
▲Figure 5.Throughput performance comparison between M-IRSA and IRSA schemes.

6 Conclusions

A pre-coding based random access scheme named M-IRSA is proposed,where no channel load estimation or additional central controller is needed to allocate the channel resource.Joint procedure of SIC iterations and local decoding is analyzed.Compared with the existing advanced random access scheme IRSA,the proposed scheme is more effective without PLR loss.