(The 54th Research Institute of China Electronics Technology Group Corporation,Shijiazhuang 050081,China)

Abstract: The high speed of low earth orbit (LEO) satellites makes the terminals at each beam tend to switch rapidly and frequently.The predictable trajectories of LEO satellites allow for predictable terminal switching,therefore a simple and highly accurate orbit prediction model is required to swiftly obtain accurate switching time.This study utilizes the simplified general perturbations (Version 4) (SGP4) model to predict the LEO satellite trajectory of WT-1,an LEO satellite developed independently by the 54th Research Institute of China Electronics Technology Group Corporation (CETC).The obtained prediction results are compared with the actual telemetry data of the WT-1,which gives the accuracy of the SGP4 predicted satellite trajectory within 1 km.The terminal entry/exit beam timing is simulated by using the SGP4 model-predicted orbit and the satellite's own telemetry data.The simulation result shows that the error between the SGP4 model-predicted terminal entry/exit beam timing and the actual timing is less than 1 s.The influence of terminal motion on prediction is discussed.The results show that the error caused by the movement of the ground terminal on the prediction is less than 0.687 s,and the SGP4 model has a definitely practical value for terminal switching determination in the LEO constellation.

Keywords:LEO;switching;SGP4;WT-1

1 Introduction

Low earth orbit (LEO) satellites operate at a low altitude,providing a low transmission delay and a low transmission loss in the satellite-ground link.Furthermore,multiple LEO satellites can form an LEO constellation to achieve a seamless global coverage.Featuring the abovementioned advantages,LEO satellite communications have been favored by more and more countries[1].However,the terminal under an LEO satellite beam has to switch to other beams for continuous communication because of the constant high-speed movement of LEO satellites.The quality of the switching method will directly affect the terminal switching delay,switching frequency,quality of service,switching failure rate,and other indicators,consequently affecting the entire system performance,which is one of the most challenging problems in the field.The satellite orbit is predictable,and thus the exact timeframe that the terminal enters a specific beam can also be predicted.It calls for excellent guidance for terminal switching,for which the critical factor is the sufficient prediction accuracy.This study utilizes the LEO satellite ephemeris[2]to predict the WT-1 satellite trajectory using the SGP4 model.The prediction results are then compared with the actual telemetry data of the WT-1 satellite to verify the SGP4 model's prediction accuracy.Then,the terminal entry/exit beam timing will be simulated with the SGP4 model's predicted-orbit and the WT-1 satellite's telemetry data.Finally,the influence of the movement of the ground terminal on the prediction will be discussed.

2 Related Research

DIAO et al.[3]verified the prediction accuracy of the SGP4 model and evaluated the accuracy of the SGP4 prediction values and the simulation results of satellite tool kit (STK) software in his study.Based on historical two-line element (TLE)data,XU et al.[4]statistically counted and generated a large number of target track prediction errors based on the fixedtrack standard prediction method,and then provided the mean and mean-variance of the track prediction errors of the SGP4 model over 7 days as a function of time.When this paper was in the works,XU et al.proposed the method[5]of comparing the historical TLE orbits of challenging minisatellite payload(CHAMP) satellites with global positioning system (GPS) precision ephemeris,which was found to be similar to our method of verifying the forecast accuracy of SGP4.However,XU et al.did not discuss the feasibility of using the SGP4 model for LEO satellite terminal switching.For the LEO satellite terminal switching,a few studies are related to the terminal switching determination based on ephemeris.SU[6]deduced the latitude and the longitude of all satellites in real time in accordance with the latitude and the longitude of an LEO satellite and narrowed down the candidate range of the target satellites on the basis of the terminal's geographic location.The satellite with the shortest distance from the terminal was selected from the candidate satellites as the switching target.However,the problem of switching between different beams of the same satellite could not be solved with this method.

3 Terminal Switching Scenarios of LEO Satellites

The terminal switching scenarios of LEO satellites are described as below.

(1) Switching between different beams of the same satellite,which is similar to the station switching in terrestrial cellular mobile communications.

As shown in Fig.1a,the source and target beams are in the same satellite.When the terminal is at the edge of the source beam,the source beam is unavailable to provide services to the terminal,and hence the terminal must switch to the adjacent target beam.When the switching occurs,the system reallocates the available channels for the terminal.

(2)Switching between two different satellites,which is similar to the station-to-station switching in terrestrial cellular mobile communications.

As shown in Fig.1b,when the terminal is at the edge of the source satellite,it must be switched to an adjacent satellite,where the inter-satellite switching is performed.When the terminal switches,a switching request is initiated to the target satellite via the interstellar link.

4 Satellite Trajectory Predictions by the SGP4 Model

The SGP4 orbital model was developed by Ken CRANFORD in 1970 for near-earth objects with flight periods that are no longer than 225 min.This model is a simplification of the extensive analytic theory of LANE and CRANFORD.It considers the following perturbations:(1) atmospheric perturbations based on a static,non-rotating,spherically symmetric atmosphere,the density of which can be described by the power law; (2) fourth-order potential harmonics (J2,J3,and J4);(3) spin-orbit resonances in synchronous and semi-synchronous orbits; and (4) the influence of the solar and lunar gravity.Among the perturbations,(3)and(4)have less influence on the LEO satellite prediction than the other two.The code of the SGP4 model is open to the public,which is very convenient for academic research and has relatively high prediction accuracy.

The TLE orbital report released by the North American Aerospace Defense Command (NORAD) in 2005 considered the effects of Earth being a non-standard sphere and various perturbations (e.g.,atmospheric resistance,solar gravity and lunar gravity),with each TLE representing a particular target in space.The position coordinates problem of the satellite in the true equator mean equinox (TEME) system can be solved by combining the TLE with the SGP4 model.This study is based on the WT-1 LEO satellite developed independently by the 54th Research Institute of CETC.Table 1 presents the main orbital parameters of the WT-1 satellite.

The TLE of the satellite for March 12,2020 was downloaded from the website:http://celestrak.com.The coordinates of the satellite's position from 11:44:10 on March 13,2020 to 11:54:10 on March 13,2020 were predicted,as shown in-Table 2.

And when you have had enough and don t want the little table any more, you have only to say, Little goat, bleat, Little table, away, and then it will vanish

5 Conversion from the WGS84 to TEME System

The telemetry data of the satellite from 11:44:10 on March 13,2020 to 11:54:10 on March 13,2020 were obtained to verify the accuracy of the satellite trajectory prediction by the SGP4 model.The satellite position coordinates under the World Geodetic System 1984 (WGS84) system are generated by the satellite's own GPS and considered to be accurate,as shown in Table 3.

The position coordinates of the WGS84 system satellite will be compared with those predicted by the SGP4 model.However,WGS84 and TEME belong to two different reference systems and must be converted to the coordinates of the same coordinate system for a comparison.First,the satellite position coordinates of the WGS84 system(B,L,H) were converted into the position vectorrECEFof the corresponding satellite in the earth-centered and earth-fixed(ECEF)system.Next,the corresponding satellite position vectorrJ2000in the J2000 system(which belongs to the earth centered inertial system) was obtained using the relevant formula.Finally,the corresponding satellite position vectorrTEMEin the TEME system was calculated.Fig.2 illustrates the conversion process.

A detailed presentation of the conversion process is showed in Ref.[7],where the satellite position coordinates of the WGS84 system were converted to the position coordinates of the TEME system through the abovementioned process that is showed in Ref.[7].Table 4 shows the results and Table 5 presents the differences from the position coordinates predicted by the SGP4 model.

The comparison shows that the difference between the satellite position coordinates predicted by the SGP4 model and the actual satellite position coordinates is within the range of 1 km.Meanwhile,the distance between the predicted and actual sub-satellite points by the SGP4 model did not exceed,where ΔrTEMEis defined as the difference between the satellite position vector predicted by the SGP4 model and the actual satellite position vector.Ris the Earth radius,andhis the satellite altitude,which is negligible compared with the satellite beam size.

6 Terminal Entry/Exit Beam Simulation

The satellite beam distribution was known.The terminal's position can be obtained from the terminal's GPS,which canbe applied to calculate the angle in the terminal-satellitebeam center and compare the angle with the radiation half-angle of the beam to determine whether the terminal enters or exits the beam.Fig.3 illustrates a beam of an LEO satellite.PointOis the intersection of the beam centerlineSOand thetangent plane of sub-satellite point.The beam radiation halfangle isα.The angle between the beam centerlineSOand thez-axis is denoted byθ.The beam centerlineSOprojection in theySxplane isSO'.The angle between theSO'and thexaxis is denoted byβ.Meanwhile,α,θ,andβwere known at the time when the antenna design was completed.Andhis the satellite altitude.The coordinates of pointO(xO,yO,zO) in the satellite's centroid orbit coordinate system were calculated as follows.

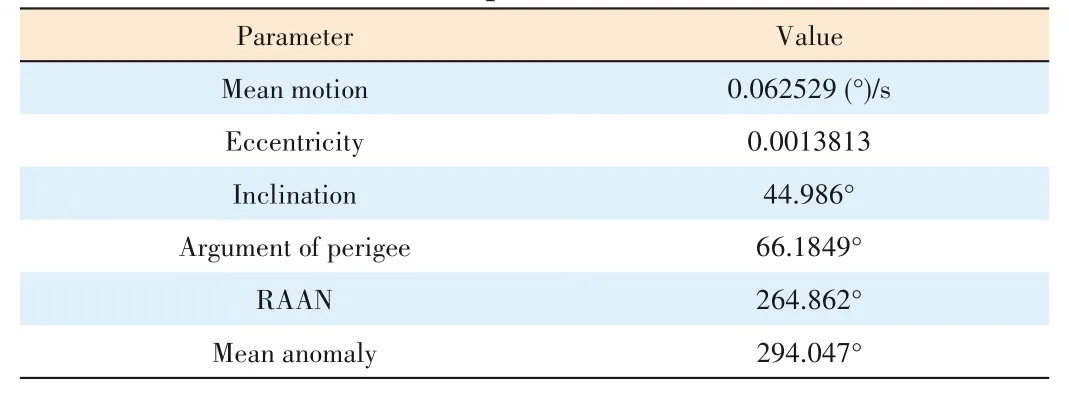
▼Table 1.WT-1 satellite orbital parameters

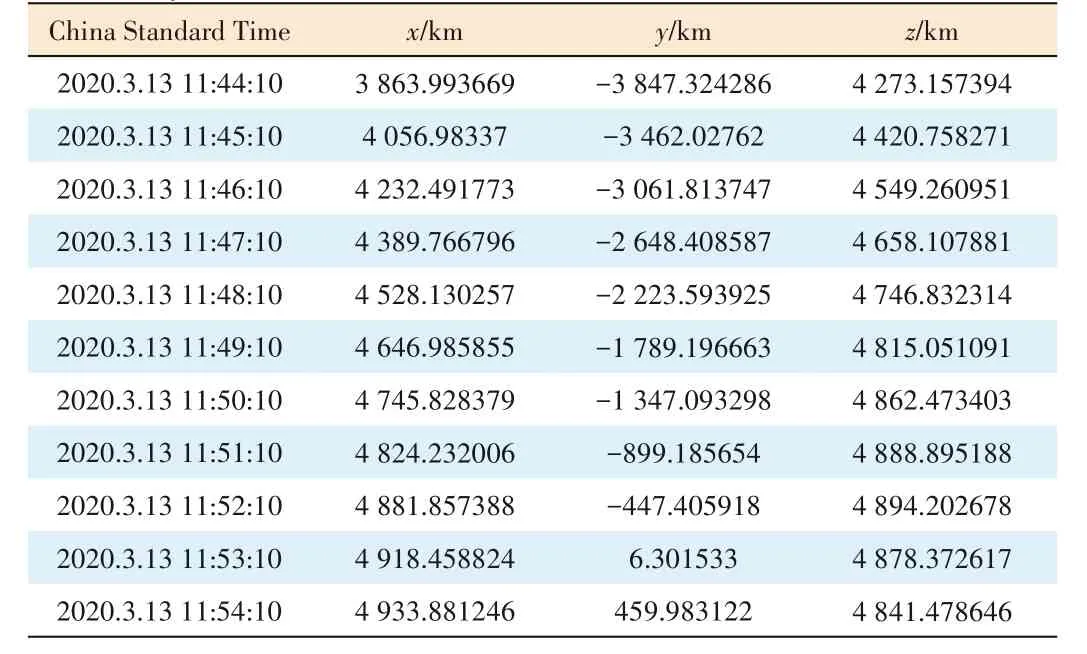
▼Table 2.Satellite locations under the true equator mean equinox(TEME)system

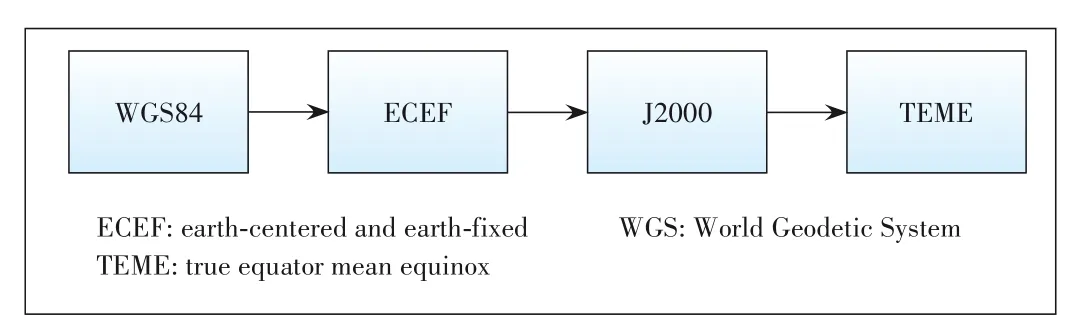
▲Figure 2.Conversion process from the WGS84 to the TEME line.

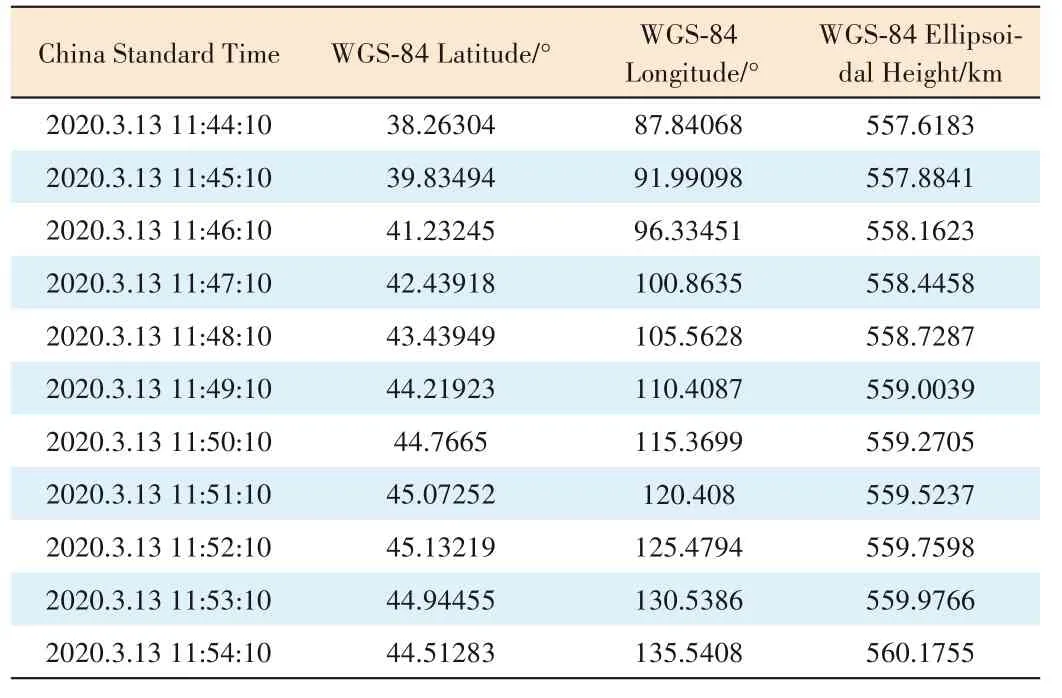
▼Table 3.Satellite locations under the WGS84 system

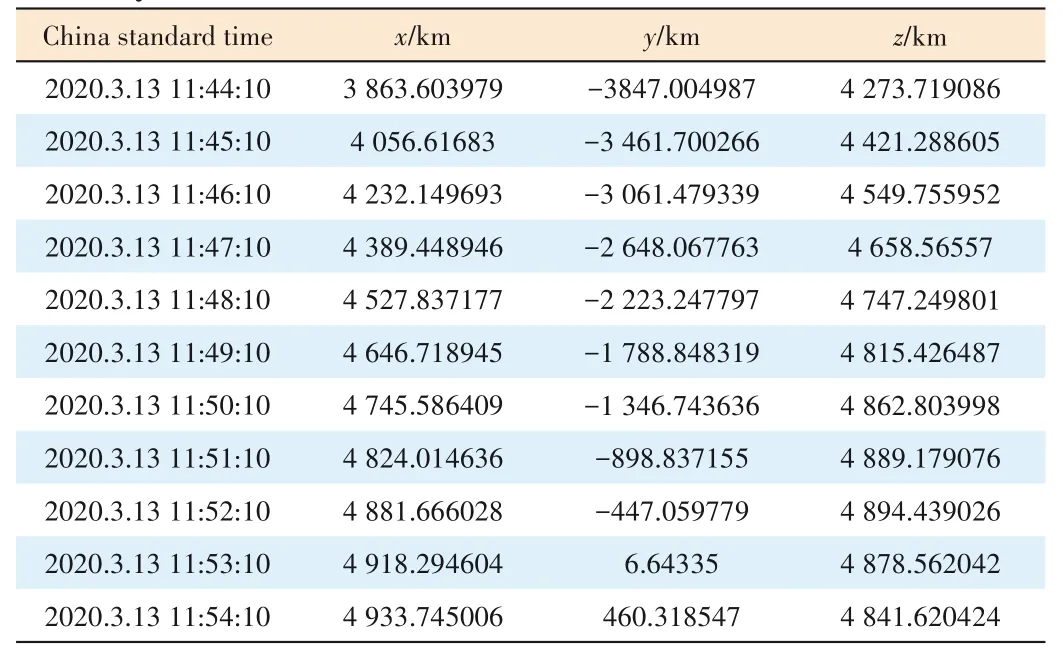
▼Table 4.Coordinates of the WGS84 system after conversion to the TEME system

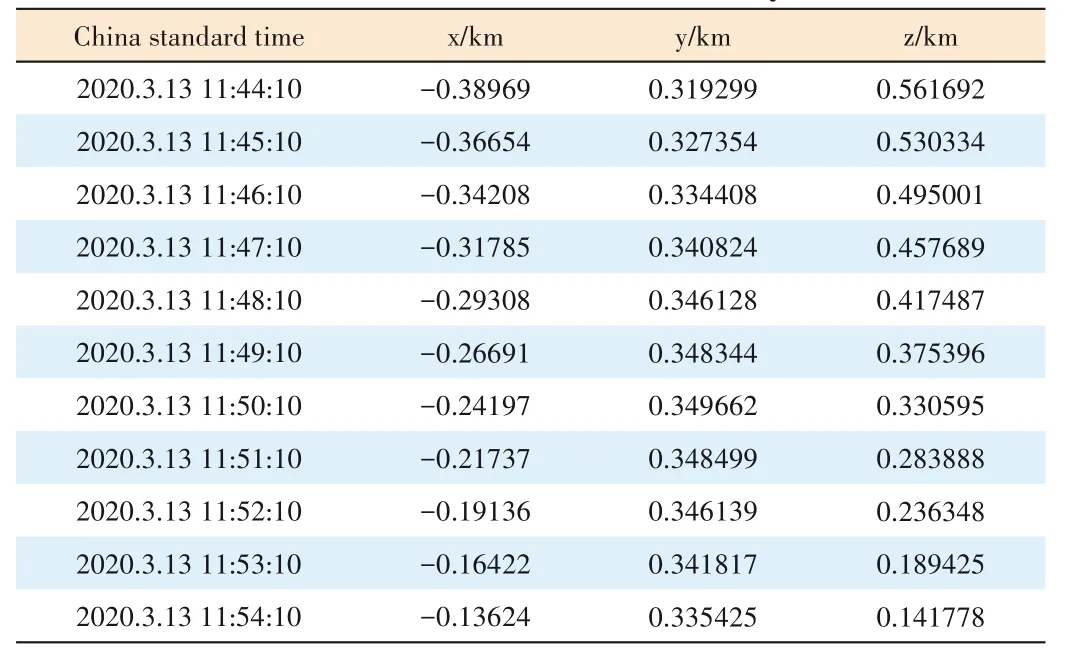
▼Table 5.Difference between the predicted coordinates of the SGP4 model and the converted coordinates of the WGS84 system

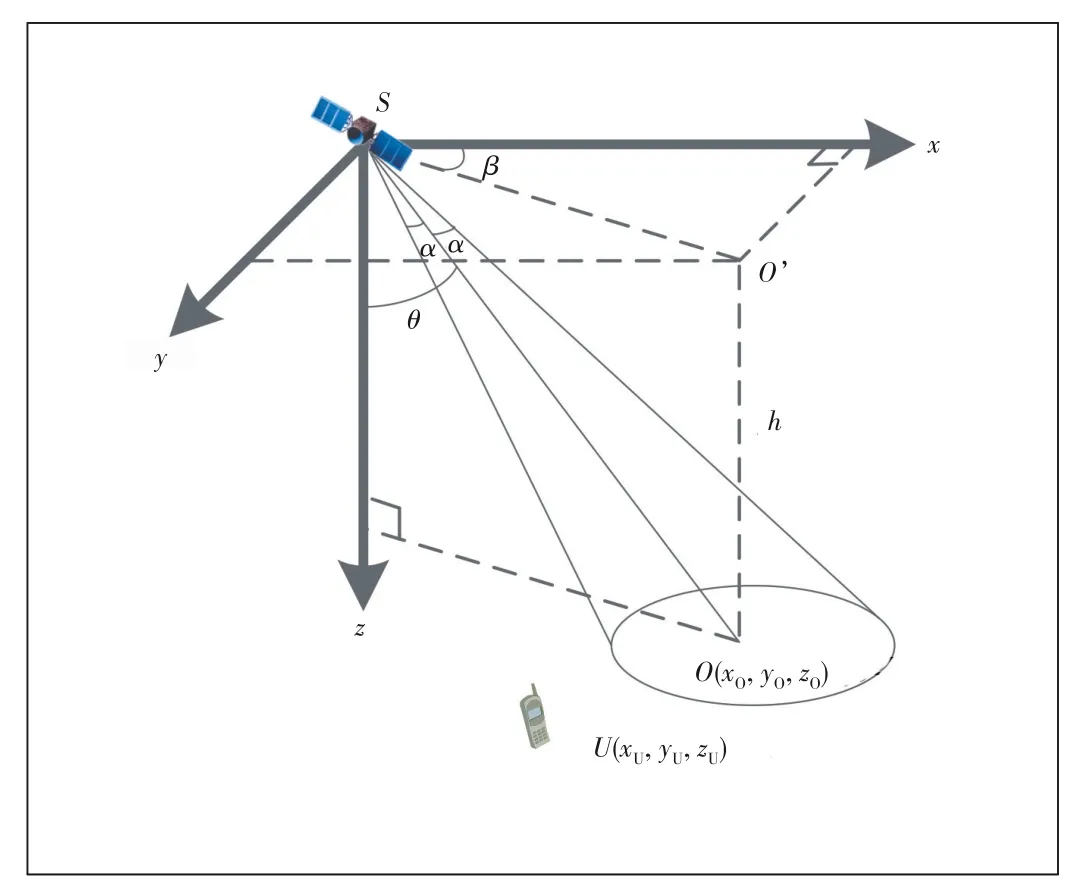
▲Figure 3.Relationship between the terminals and the satellite beams.

The terminal's coordinates are in the WGS84 reference system,while the satellite beam distribution is in the centroid orbit coordinate system.The terminal coordinates must be converted into a satellite centroid orbit coordinate system to calculate the angle in the terminal-satellite-beam center.The satellite's centroid orbit coordinate system is centered on the satellite's mass point.Thez-axis is pointed to the Earth's center by the satellite,thex-axis is the tangential direction of the satellite operation,and they-axis conforms to the right-hand rule.By makingrandvas the absolute position and the absolute velocity vectors of the reference satellite in the geocentric inertial coordinate system,theδr0=(x0,y0,z0)Tvector of the terminal relative to the satellite in the centroid orbit coordinate system can be calculated according to the following Eqs.(5),(6)and(7)[8].

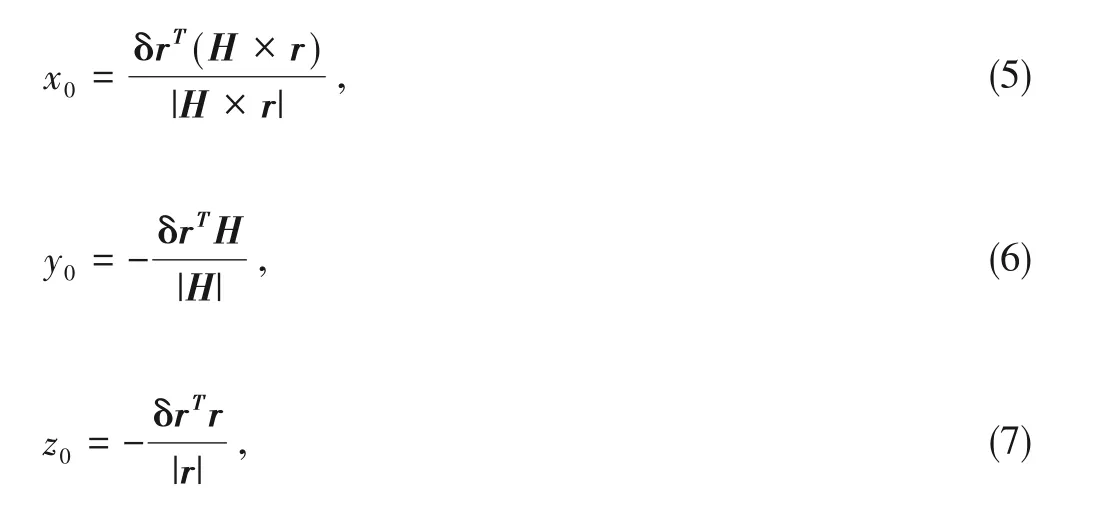
whereH=r×v.Hererandvdenotes the position and velocity vectors of the satellite in the geocentric inertial coordinate system,andδris the position vector of the terminal relative to the satellite in the geocentric inertial coordinate system.

The terminal obtains its position coordinates via GPS and converts the coordinates toU(xU,yU,zU) using the above conversion formula,where

With the satellite movement,the terminal is within the beam coverage area when ∠USO≤∠α,otherwise,it is not.Similarly,the timing of the terminal's entry/exit of all beams from and to the satellite can be calculated based on the same method.

This simulation was implemented using the C programming language.The flowchart is shown in Fig.4.

We assumed herein that the satellite has six beams to achieve 0° to ±60° coverage of the circular region as shown in Fig.5.

The terminal coordinates are as follows:latitude:37°,longitude:113° and altitude:0 m.A simulation of the terminal's entry/exit beam timing was performed by using the SGP4 modelpredicted satellite trajectory,and Table 6 presents the results.A simulation of the terminal's entry/exit beam timing was also performed using the satellite telemetry data,and Table 7 shows the simulation results.

The sampling period of the telemetry data was 1 s,and thus,the calculation of the terminal entry/exit beam moment can only be accurate to seconds.A conclusion that the error between the SGP4-predicted orbit simulated terminal beam and the actual telemetry data simulated terminal beam was not greater than 1 s could be reached by comparing Tables 6 and 7.

7 Influence of Terminal Speed on SGP4 Model Prediction

The terminals discussed in this study are limited to ground terminals.When the terminal is a ground fixed terminal,only the SGP4 model error and the TLE error will affect the prediction.But if the speed of the terminal is not zero,the movement of the terminal will also cause errors in the prediction.The scenario of using the SGP4 model to predict the terminal entry/exit beam is shown in Fig.6.

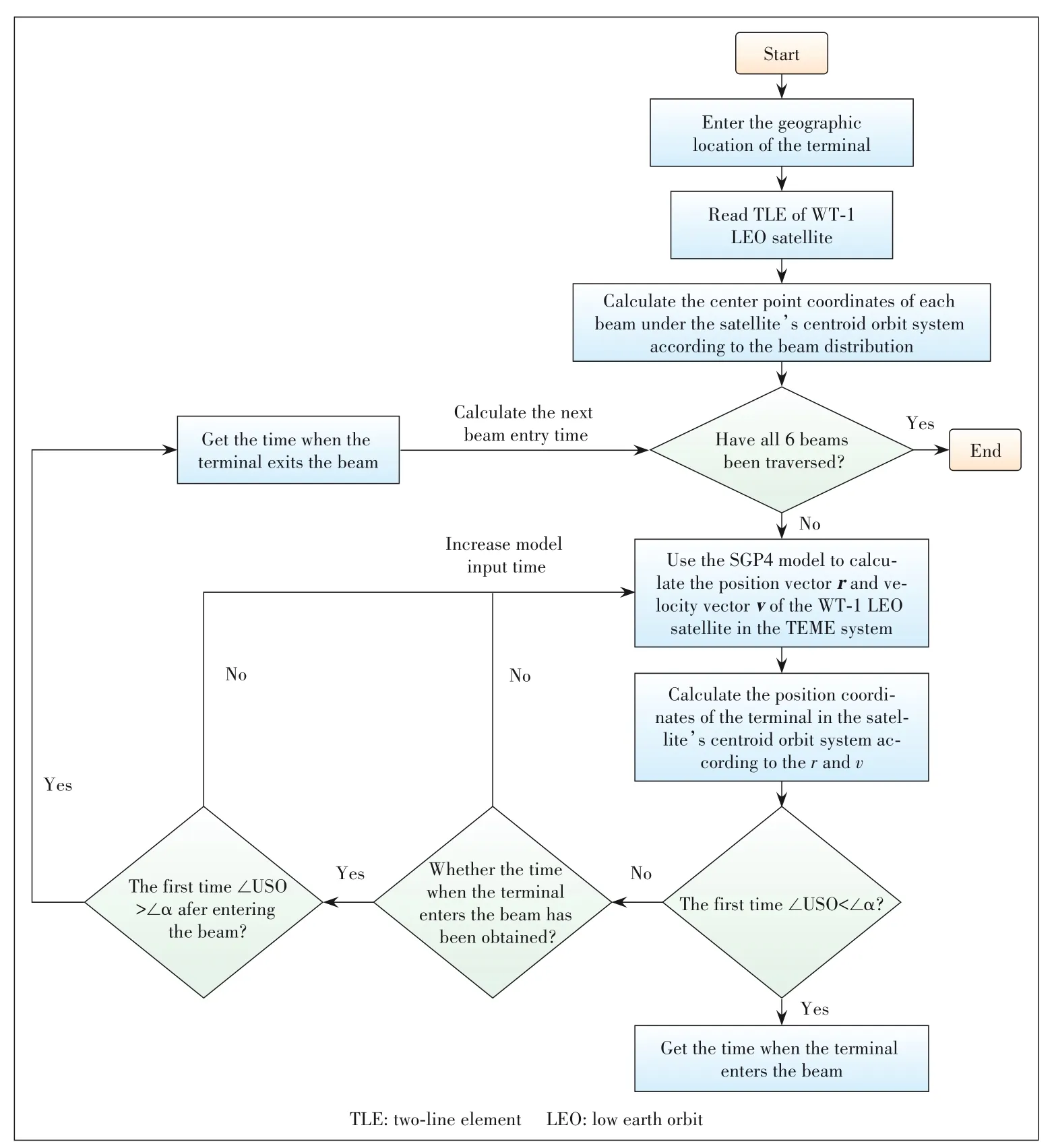
▲Figure 4.C language programming implementation flowchart.

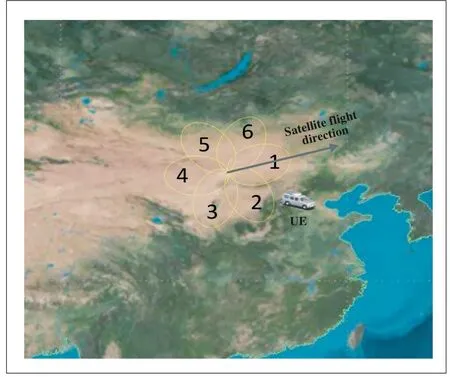
▲Figure 5.Satellite beam distribution.

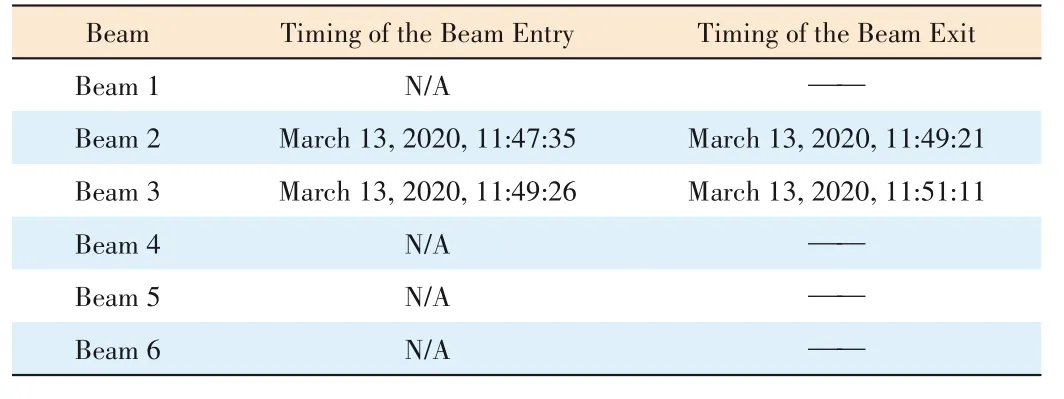
▼Table 6.SGP4-predicted orbital simulation of the terminal entry/exit beam timing

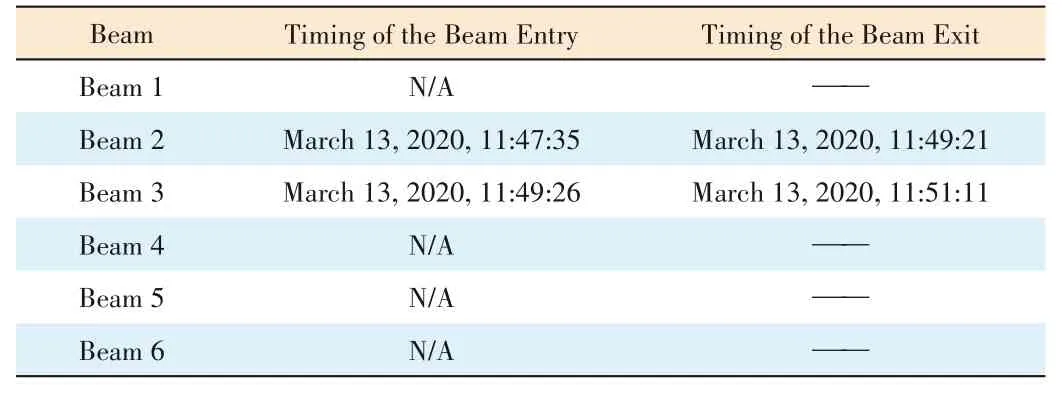
▼Table 7.Telemetry data of the terminal entry/exit beam timing simulation

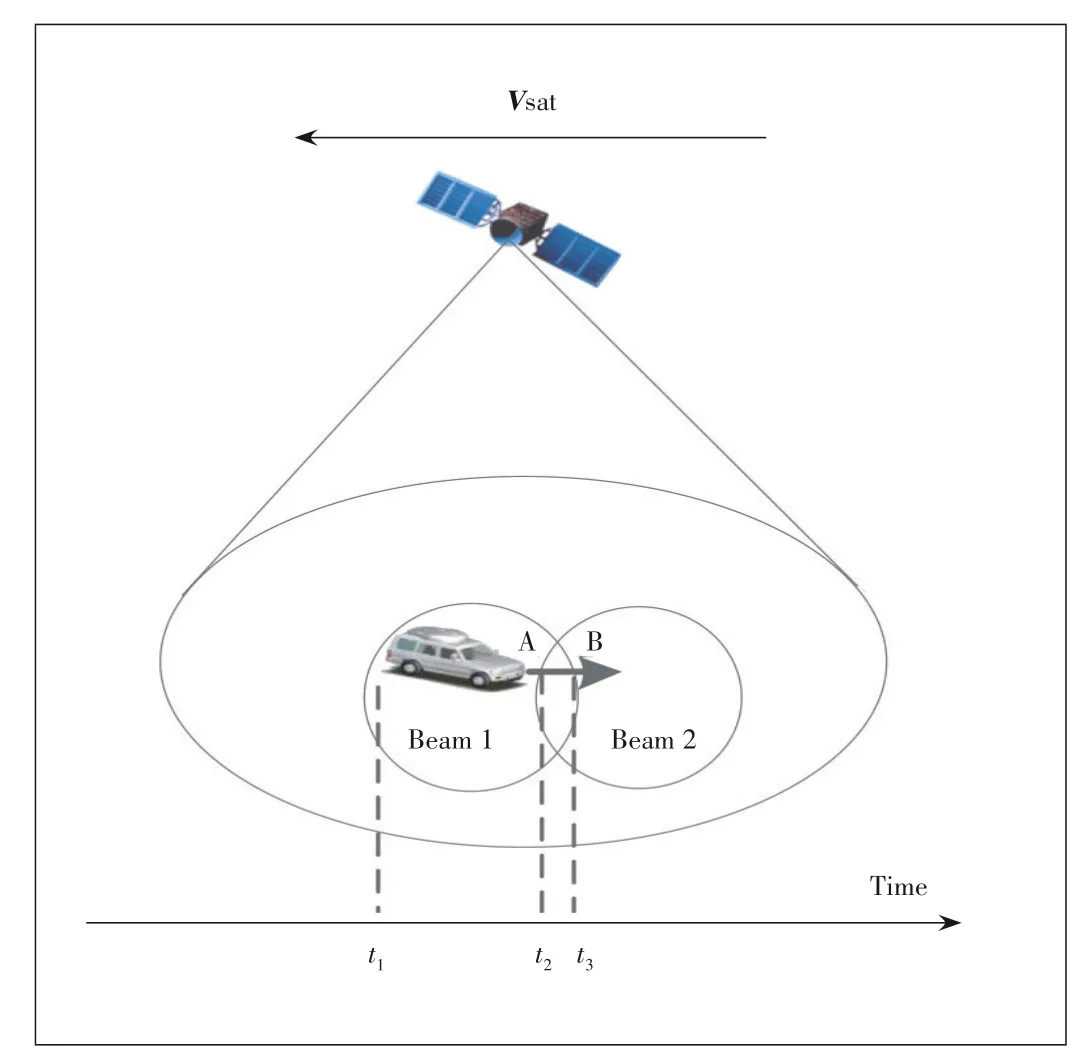
▲Figure 6.Predicted terminal entry/exit beam scenario.

In Fig.6,t1is the moment when the SGP4 model is invoked andt2is the moment when the terminal enters Beam 2.Point A is the position where the terminal enters Beam 2,andt3is the moment when the terminal leaves Beam 1.Point B is the position where the terminal enters Beam 1.t2,t3,A and B are all predicted values of SGP4 model.Assume the speed of terminal isvUE,and its magnitude and direction remain constant.Then,the distance error between the terminal and point A after time(t2-t1)is:

The speed of the satellite relative to the terminal isv,and its value is:

Then,when the satellite movement distance is|vsat|×(t2-t1),considering terminal motion,the time taken is:

So,the predicted time error of entering Beam 2 due to the terminal speed is:(t2-t1) -t.

Take Iridium as an example,the orbit altitude of the satellite is 780 km,and the moving speed of the satellite is about 7.52 km/h.Each satellite carries 3 L-band antennas,which generate 48 spot beams on the ground,and the diameter of each spot beam coverage area is about 400 km.The diameter of a single satellite coverage area is about 4 500 km[9].Generally,the overlap area of satellite beams accounts for about ten percent of the entire beam coverage area[10].Without considering the terminal speed,the time for the terminal to pass through the overlap area is about 5 s.The fastest speed of highspeed trains can reach 350 km/h.When the high-speed train is connected to Beam 1,the SGP4 model is called,hence,t2-s and.When the terminal and the satellite move towards or relative to each other,the absolute value of the time error is the largest,that the time error caused by the movement of the terminal is much smaller than the time for the terminal to pass through the overlap area.

8 Conclusions

This study adopts the SGP4 model to predict the TLE satellite trajectory.Furthermore,we verify that the prediction accuracy of the SGP4 model on the trajectory of the LEO satellite is less than 1 km through a comparison with the telemetry data of the LEO satellite itself.The simulation of the terminal entry/exit beam timing between the predicted orbit and the telemetry data of the satellite itself shows that the error between the predicted and actual terminal entry/exit beam timing is within 1 s.Finally,we discuss the impact of terminal motion on prediction.The error caused by the movement of the ground terminal on the prediction does not exceed 0.687 s.The time error caused by the SGP4 model and the movement of the terminal is much smaller than the time for the terminal to pass through the overlap area.Furthermore,the SGP4 model is less complex,indicating that it has a certain practical value for determining the terminal switching of LEO constellation.