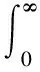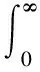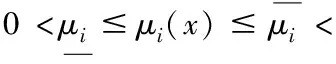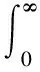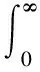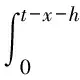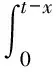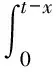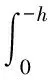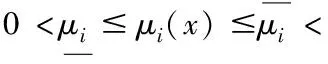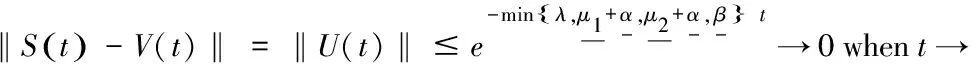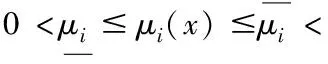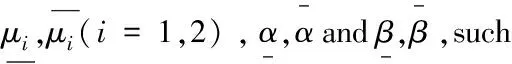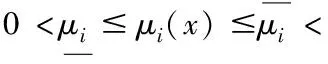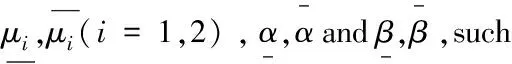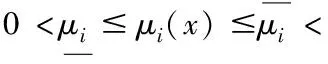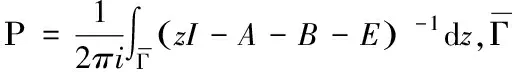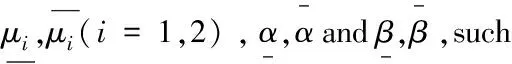Alim MIJIT, Oghuljan AINI

(1.Xinjiang Radio & TV University,Urumqi 830049,China;2.No.2 Middle School of Urumqi,Urumqi 830000,China)

Abstract:We consider an M/G/1/1 queueing model with unreliable server and no waiting capacity in this paper.Firstly we show that the underlying operator corresponding to the M/G/1/1 queueing model generates a positive contraction C0-semigroup T(t)and verify that T(t)is a quasi-compact operator.Next,we derive that the imaginary axis points beside zero belongs to the corresponding operator’s resolvent set.Thus,by these above results we conclude that the nonnegative time-dependent solution of the M/G/1/1 queueing system converges strongly to the steady-state solution of the system.

Key words:M/G/1/1 queueing model with unreliable server and no waiting capacity;quasi-compact operator;resolvent set

The different kinds of M/G/1/1 queueing systems have been widely used in management science,operations reasearch problems,communication networks and computer modeling,because of their wide applicability[1-4,7-9].

In 2002 KUMAR et al.consider an M/G/1/1 queueing system with no waiting room,and by using supplementary variable technique[5]established the corresponding system model.In this paper,use the same idea of the paper[6],we discuss the asymptotic behavior of the system solution of the M/G/1/1 queue with no waiting room by analyzing quasi-compactness of the system operator.

According to paper[7-8],the M/G/1/1 queueing model with unreliable server and no waiting room can be described by the following group of equations:

(1)

(2)

(3)

P1(0,t)=λP0(t),

(4)

(5)

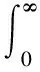
(6)

P0(0)=1,Pi(x,0)=0,i=1,2,F,

(7)

here(x,t)∈[0,)×[0,);P0(t)as the probability that at momenttthere is no any customer in the queue and server in the system is idle;Pj(x,t)represents the probability at momenttit is providingjthtype service(j=1,2)with an elapsed service timex;PF(x,t)gives the probability that the server in the model is being repaired at the momenttwith the elapsed repair timex;numberλrepresents constant mean arrival rate of the arrivals of the customers;pgives the probability that after finishing the regular service,the customer desires to receive the optional service;qgives the probability that after finishing the regular service,the customer immediately leaves the queueing system;wherep+q=1;α(x)dxgives probability the server in this model will fail in the interval(x,x+dx)under the condition that the server has not failed untill timex;β(x)dxdenotes probability the server in this queue will end the repair during(x,x+dx)by the condition that the repair of the server has not completed untill timex;μj(x)dx(j=1,2)gives the conditional probability that the regular(or optional)service will be finished between the interval(x,x+dx)on the condition that the same service has not finished untill timex.

1 Formulation of the system

Firstly,the mathematical model of this sytem converted as an abstract Cauchy problem(ACP)by defining a corresponding state space.For to do that,we introduce

and denote the state spaceXas follows

It is not difficult to prove thatXis a Banach space.Next,we define some operators and the operators domains.

Then the above system of integro-differential equations(1)-(7)can be described as an ACP in the state spaceX:

(8)

In paper[8],the author obtained the following result by using strong continuous semigroup theory.

Theorem1 Nonnegative contractionC0-semigroupT(t)is generated by the operatorA+B+E.

By applying the proof process as same as Theorem 1.1 in[8],we immediately conclude the following corollary.

Corollary1 OperatorA+Bgenerates a nonnegative contractionC0-semigroupS(t).

2 Main Results

Lemma1 If forφ∈X,P(x,t)=(S(t)φ)(x)is a solution of the following system

(9)

then

whenx

whenx>t.WherePi(0,t-x)(i=1,2,F)are given by(4)-(6).

Proof SincePis a solution of the system(9),soP(x,t)satisfy

(10)

(11)

(12)

P1(0,t)=λP0(t),

(13)

(14)

(15)

P0(t)=φ0,Pi(x,0)=φi(x),i=1,2,F.

(16)

If we setζ=x-tandQi(t)=Pi(ζ+t,t),then from(11)and(12),we obtain

(17)

(18)

Ifζ<0(equivalentlyx

Qi(-ζ)=Pi(-ζ+ζ,-ζ)=Pi(0,-ζ)=Pi(0,t-x)(i=1,2,F),

and using new integral variabley=ζ+τ,we deduce

(19)

(20)

Ifζ>0(i.e.x>t),then integrating(17)and(18)from-ζtot,using

Qi(0)=Pi(ζ,0)=φi(ζ)=φi(x-t)(i=1,2,F),

and using new integral variableη=ζ+τwe derive

(21)

(22)

(19)-(22)show that the result of this lemma is right.

Forφ∈X,if we define two operators as follows,

thenS(t)φ=U(t)φ+V(t)φ,?φ∈X.

In[10],the author deduced the result in the following:

Lemma2 AssumeYis a closed subset ofXandYis bounded,thenYis relativlely compact when and only when it satisfies the following two conditions:

Proof From the definition ofV(t)and the above Lemma 2,it suffices to prove that the conditions(1)in above Lemma 2.Forx,h∈[0,t),x+h∈[0,t),we have

(23)

If the right side of above(23)can be proved converges to zero uniformly,then we deduce our desired result.So,next we will estimate each term in(23).

By using(13)-(15)and Lemma 1 we have

|P1(0,t-x-h)|=|λP0(t-x-h)|=λ|φ0|e-λ(t-x-h)≤λ|φ0|≤λ‖φ‖X.

(24)

(25)

(26)

By(24)-(26)we will estimate that the first term and third term of the(23)as follows:

→0 as |h|→0,uniformly forφ.

(27)

(28)

Next,we will estimate that the second term and the fourth term in(23).

By using Lemma 1,(13)-(15)and Lipschitz continuity(without loss of generality assume that the Lipschitz constants is equal to 1)we derive

|P1(0,t-x-h)-P1(0,t-x)|=λ|P0(t-x-h)-P0(t-x)|

=λ|φ0‖e-λ(t-x-h)-e-λ(t-x)|≤λ‖φ‖X|e-λ(t-x-h)-e-λ(t-x)|

→0 as |h|→0,uniformly forφ.

(29)

|P2(0,t-x-h)-P2(0,t-x)|

+ph‖φ‖X→0 as |h|→0,uniformly forφ.

(30)

|PF(0,t-x-h)-PF(0,t-x)|

+2h‖φ‖X→0 as |h|→0,uniformly forφ.

(31)

Therefore,by combining(27)-(31)with(23),we obtain forx,h∈[0,t),x+h∈[0,t)

(32)

Ifh∈[-t,0),x∈[0,t),then fromPi(x+h,t)=0(i=1,2,F)forx+h<0,we derive

(33)

Sincex+h∈[0,t)forx∈[0,t),h∈[-t,0),similar way to(32)we have for the first term in(33)

(34)

By using Lemma 1,(24)-(26)we estimate the second term in(33)as follows:

(35)

By the same way we deduce

(36)

Combining(34)-(36)with(33)we obtain,forh∈[-t,0)

(37)

(32)and(37)show that the result of this theorem is right.

thenU(t)satisfies

Proof For anyφ∈X,from the definition ofU(t),Lemma 1 and using new integral variableτ=x-t,we deduce

(38)

(38)shows that the result of this theorem is right.

By applying above Theorem 2 and Theorem 3 in this paper we have

From above result and the Definition 2.7 in Nagel[11],we conclude the result in the following:

thenS(t)is a quasi compact operator on the state spaceX.

OperatorEis a compact operator on the state spaceX,because of the operatorE:X→R4is a linear and bounded operator,therefore from the Theorem 4 in this paper and the Proposition 2.9 in Nagel[11],we conclude

thenT(t)is a quasi-compact operator onX.

In paper[8],Mijit obtaineds(A+B+E)=0.This result together with Corollary 2,Theorem 1 and Remark 2.2(c)and Theorem 2.1 in[11],we conclude the result in the following.

then there exists suitable constantδ>0 and Μ>1 and positive projection Ρ with rank 1,such that

‖T(t)-Ρ‖≤Μe-δt,

By Combining Lemma 4.1 and Lemma 4.3 in paper[8],Theorem 1,Corollary 2 in this paper with Proposition 2.9 and Theorem 2.10 in[11]we know:

{γ∈σ(A+B+E)|Reγ=0}={0}.

In other words,{γ∈C|Reγ>0orγ=ic,c≠0,c∈R} belongs to the resolvent set ofA+B+E.Thus by using Theorem 1.96 in[12],we deduce the result in the following:

then the dynamic solution of the queueing system(8)strongly converges to the steady-state solution of the system,that is

where theP(x)in the limit is an eigenvector,which is corresponding to the underlying operator’s eigenvalue 0.

If the expression of the projection Ρ in the Theorem 5 can be obtained,then we will conclude that the dynamic solution of the queueing system(8)exponentially converges to the steady-state solution of the queueing system,which is the next research work of ours.