白瑞蒲, 吳嬰麗

(河北大學(xué) 數(shù)學(xué)與信息科學(xué)學(xué)院, 河北 保定 071002)

1 引言與預(yù)備知識(shí)

目前, 關(guān)于多元李代數(shù)分類的研究已有很多結(jié)果： 文獻(xiàn)[1-3]研究了多元李代數(shù)的結(jié)構(gòu); 文獻(xiàn)[4-6]分別對(duì)特征2域上(n+1)-維n-李代數(shù)及特征零域上(n+2)-維n-李代數(shù)和度量n-李代數(shù)進(jìn)行了分類, 證明了不存在特征2域上單的(n+2)-維n-李代數(shù); 文獻(xiàn)[7-8]從n-李代數(shù)的生成指標(biāo)出發(fā), 對(duì)具有生成指標(biāo)為n的n-李代數(shù)進(jìn)行了分類. 本文主要研究特征零域F上β(L)=m-n+1的m-維非交換n-李代數(shù)[9-10]的結(jié)構(gòu), 并對(duì)具有特殊導(dǎo)代數(shù)維數(shù)的n-李代數(shù)進(jìn)行分類, 其中β(L)是非交換n-李代數(shù)L的Abel理想的最大維數(shù)[11].

n-李代數(shù)L[9]是域F上具有線性運(yùn)算[,…,]:L∧n→L的線性空間, 且對(duì)任意x1,…,xn,y2,…,yn∈L, 滿足下列恒等式:

設(shè)L是n-李代數(shù),A是L的子空間, 若A滿足[A,…,A]?A([A,L,…,L]?A), 則稱A為L(zhǎng)的子代數(shù)(理想)[10]. 若[A,…,A]=0([A,A,L,…,L]=0), 則稱A為L(zhǎng)的交換子代數(shù)(Abel理想). 特別地, 由[x1,…,xn]生成的子代數(shù)稱為L(zhǎng)的導(dǎo)代數(shù), 記為L(zhǎng)1, 其中x1,…,xn為L(zhǎng)中的任意元素. 若L1≠0, 則稱L為非交換n-李代數(shù).Z(L)={x∈L|[x,y1,…,yn-1]=0, ?y1,…,yn-1∈L}稱為L(zhǎng)的中心. 顯然,Z(L)是L的Abel理想. 設(shè)L為非交換的n-李代數(shù), 記β(L)為L(zhǎng)的Abel理想的最大維數(shù).

引理1[11]設(shè)L為m-維非交換n-李代數(shù), 則m≥n,β(L)≤m-n+1, 且當(dāng)β(L)=m-n+1時(shí),L1?I, 其中I是任意滿足dimI=β(L)的Abel理想.

本文規(guī)定F是特征為零的域,L是F上的n-李代數(shù),I是L的具有最大維數(shù)的Abel理想, 對(duì)S?L, 記〈S〉為S張成的子空間.

2 主要結(jié)果

2.1 dim L1=1時(shí)n-李代數(shù)的分類

定理1設(shè)L為m-維n-李代數(shù), 且β(L)=m-n+1, dimL1=1, 則dimZ(L)=m-n, 且在同構(gòu)意義下有且僅有如下兩類: 1) [x2,xm-n+2,…,xm]=x1; 2) [x1,xm-n+2,…,xm]=x1. 其中{x1,…,xm}為L(zhǎng)的一組基.

證明: 由引理1可知L1?I. 設(shè){x1,…xm}是L的一組基, 其中x1,…,xm-n+1∈I,L1=Fx1, 則有

L1=[L,…,L]=[I,xm-n+2,…,xm]=Fx1.

如果L1?Z(L), 不妨設(shè)[xi,xm-n+2,…,xm]=λix1,λi∈F,λ2=1, 2≤i≤m-n+1. 做x1,…,xm的基變換, 將xi置換成xi-λix2, 則有[xi,xm-n+2,…,xm]=0,i≥3, 得到1), 并且Z(L)=〈x1,x3,…,xm-n+1〉, 因此dimZ(L)=m-n. 如果L1Z(L), 不妨設(shè)[xi,xm-n+2,…,xm]=λix1,λi∈F,λ1=1, 1≤i≤m-n+1. 同理討論可得2), 并且Z(L)=〈x2,…,xm-n+1〉, dimZ(L)=m-n. 根據(jù)L1是否含于Z(L)可知1)與2)不同構(gòu). 證畢.

2.2 dim L1=2 時(shí)n-李代數(shù)的分類

定理2設(shè)L為m-維n-李代數(shù), 且β(L)=m-n+1, dimL1=2, 則dimZ(L)=m-n-1, 且在同構(gòu)意義下有且僅有如下幾類：

其中{x1,…,xm}為L(zhǎng)的一組基.

證明: 由引理1可知L1?I. 設(shè){x1,…,xm}為L(zhǎng)的一組基, 且I=〈x1,…,xm-n+1〉,L1=〈x1,x2〉. 下面分3種情形討論:

(i)L1?Z(L). 此時(shí)[x1,L,…,L]=[x2,L,…,L]=0. 不妨設(shè)[x3,xm-n+2,…,xm]=x1+μx2, [x4,xm-n+2,…,xm]=λx1+x2, [xi,xm-n+2,…,xm]=λix1+μix2, 其中λ,μ,λi,μi∈F, 5≤i≤m-n+1. 做x1,…,xm的基變換, 將x1,x2,xi分別置換成x1+μx2,λx1+x2,xi-λix3-μix4, 5≤i≤m-n+1, 則有[xi,xm-n+2,…,xm]=0,i≠3,4, 得到1), 并且Z(L)=〈x1,x2,x5,…,xm-n+1〉, dimZ(L)=m-n-1.

(ii)L1Z(L)且L1∩Z(L)=Fx1. 此時(shí)[x2,xm-n+2,…,xm]≠0, 不妨設(shè)

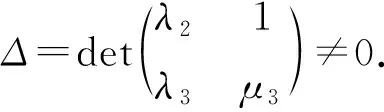
(iii)L1∩Z(L)=0. 此時(shí)[x1,xm-n+2,…,xm]與[x2,xm-n+2,…,xm]為線性無關(guān)的向量. 設(shè)A=〈x1,x2,xm-n+2,…,xm〉, 則A是(n+1)-維子代數(shù), 且dimA1=2. 由文獻(xiàn)[5]中定理3.2可知, 在同構(gòu)意義下A僅是如下情形之一:

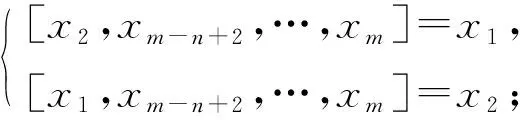
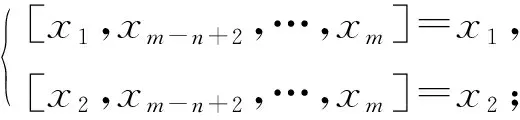
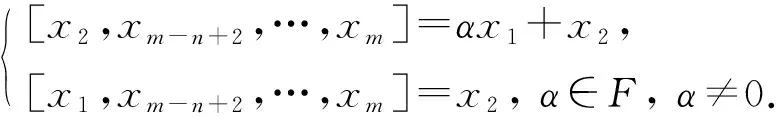
與上述討論類似可知, 當(dāng)A分別為情形①,②,③時(shí),L分別同構(gòu)于4),6),5), 且Z(L)=〈x3,…,xm-n+1〉, dimZ(L)=m-n-1. 證畢.

2.3 dim L1=3時(shí)n-李代數(shù)的分類

定理3設(shè)L為m-維n-李代數(shù), 且β(L)=m-n+1, dimL1=3, 則dimZ(L)=m-n-2, 且在同構(gòu)意義下有且僅有如下幾類:

其中{x1,…,xm}為L(zhǎng)的一組基.

證明: 假設(shè)I=〈x1,…,xm-n+1〉為L(zhǎng)的(m-n+1)-維Abel理想, 則L=I〈xm-n+2,…,xm〉, 且L1=[I,xm-n+2,…,xm]?I. 不妨設(shè)L1=〈x1,x2,x3〉.

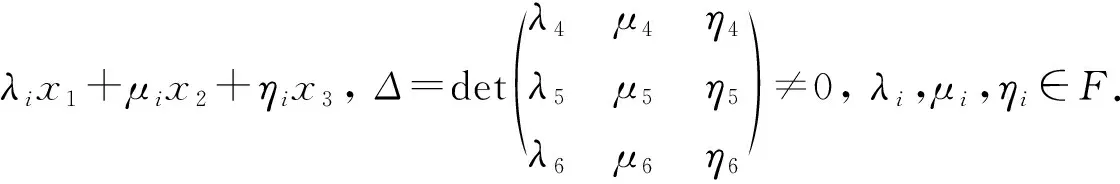
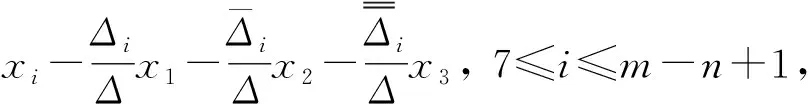
(ii)L1Z(L)且dim(L1∩Z(L))=1. 此時(shí)A=〈x1,x2,x3,xm-n+2,…,xm〉為(n+2)-維子代數(shù), 且dimA1=2. 由文獻(xiàn)[5]中定理3.2可知,A同構(gòu)于下列情形之一:

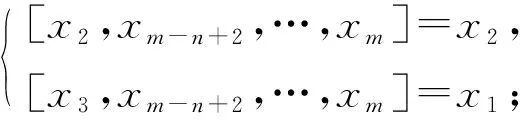
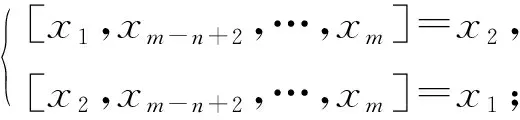
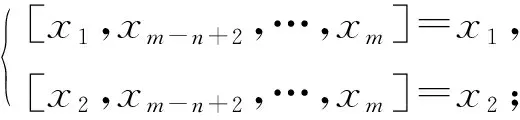
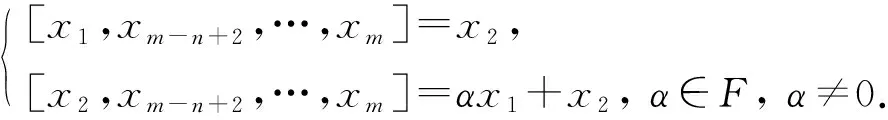
不妨設(shè)[xi,xm-n+2,…,xm]=λix1+μix2+ηix3,λiμiηi∈F,η4=1, 4≤i≤m-n+1.

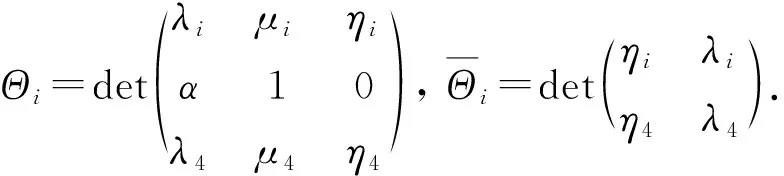
(iii)L1≠Z(L)且dim (L1∩Z(L))=2. 此時(shí)[x3,xm-n+2,…,xm]≠0, 且A=〈x1,x2,x3,xm-n+2,…,xm〉為(n+2)-維子代數(shù), dimA1=1. 由文獻(xiàn)[5]中定理3.2可知,A僅為如下情形:

[x3,xm-n+2,…,xm]=x1或[x3,xm-n+2,…,xm]=x3.

因此,L是如下兩種情形:

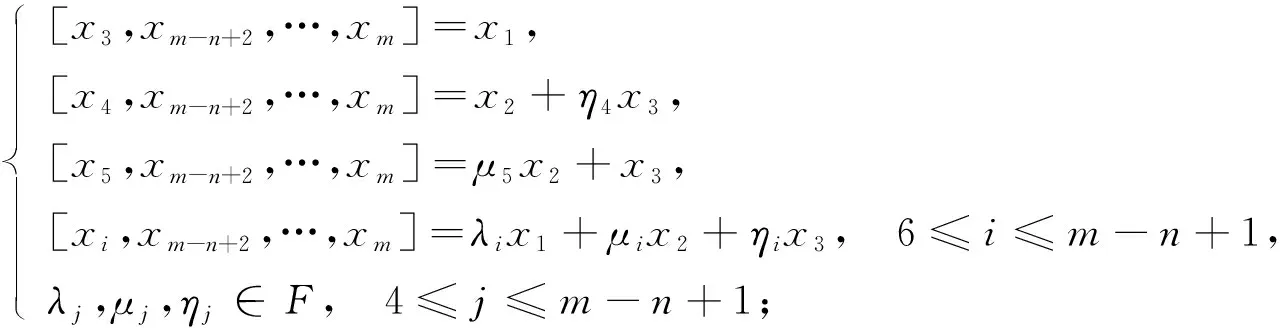
(1)

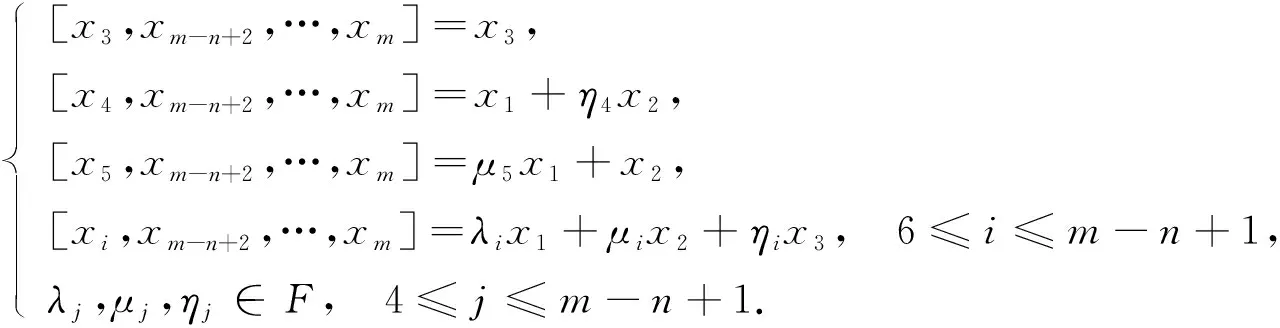
(2)

如果L為式(1), 則將x2,x3,xi分別置換成x2+η4x3,μ5x2+x3和xi-λix3-μix4-ηix5, 6≤i≤m-n+2, 得到3), 且Z(L)=〈x1,x2,x6,…,xm-n+1〉, dimZ(L)=m-n-2. 如果L為式(2), 則將x1,x2,xi分別置換成x1+η4x3,μ5x1+x2,xi-λix4-μix5-ηix3, 6≤i≤m-n+2, 得到2), 且Z(L)=〈x1,x2,x6,…,xm-n+1〉, dimZ(L)=m-n-2.

由于3)的冪零性可知2)不同構(gòu)于3).

(iv)L1∩Z(L)=0. 此時(shí)[xi,L,…,L]≠0(i=1,2,3)是線性無關(guān)的向量. 因此,A=〈x1,x2,x3,xm-n+2,…,xm〉為(n+2)-維子代數(shù), 且dimA1=3. 由文獻(xiàn)[5]中定理3.2可知,L有且僅有如下情形:

類似討論各種情形, 分別做適當(dāng)?shù)幕儞Q可得不同構(gòu)的n-李代數(shù)9)～11), 且Z(L)=〈x4,…,xm-n+1〉, dimZ(L)=m-n-2. 證畢.

2.4 β(L)=m-n+1且Z(L)?L1時(shí)n-李代數(shù)L及其導(dǎo)代數(shù)L1的維數(shù)

定理4設(shè)L為m-維n-李代數(shù),β(L)=m-n+1,Z(L)?L1, 則當(dāng)dimL1=1時(shí),n≤m≤n+1; 當(dāng)dimL1=2時(shí),n+1≤m≤n+3; 當(dāng)dimL1=3時(shí),n+2≤m≤n+5.

證明: 當(dāng)dimL1=1,2時(shí), 分別由定理1和定理2可得結(jié)論. 當(dāng)dimL1=3時(shí), 根據(jù)定理3可知, 當(dāng)L是1)時(shí),m=n+5;L是2)和3)時(shí),m=n+4; 如果L是4)～8), 則m=n+3; 如果L是9)～11), 則m=n+2. 證畢.

定理5設(shè)L為m-維n-李代數(shù), 且β(L)=m-n+1,Z(L)?L1. 如果dimL1=r, 則(m-n+1)/2≤r≤m-n+1.

證明: 假設(shè)dimZ(L)=t, 則0≤t≤r. 設(shè){x1,…,xt,…,xm-n+1,xm-n+2,…,xm}是L的一組基, 其中I=〈x1,…,xm-n+1〉,Z(L)=〈x1,…,xt〉,L1=〈x1,…,xr〉. 不妨設(shè)