Some Results on Rewritability in Modal Logics over Tree Models*
Shanshan Du
Abstract.We have investigated locally equivalent and m-conservative rewritabilities in modal logics over tree models.The modal languages studied in this paper are ML,MLI,MLG and MLGI.
1 Introduction
Over the past 100 years,many artificial languages in distinct expressiveness powers and complexity degrees have been introduced.They range from classical first-order and higher-order predicate languages to a large variety of modal languages.
Different types of languages may be“expressed”by other languages.For example,it is well known that each ML-formula is locally equivalently rewritable into a first-order formula over models.However,the converse does not hold:
? There are fisrt-order formulas that cannot be locally equivalently rewritable into an ML-formula.
van Benthem Characterization Theorem in[2]characterizes when exactly a first-order formula is locally equivalently rewritable into an ML-formula.Following van Benthem Characterization Theorem,(locally)equivalent rewritability has become an important and active research problem in modal logic([4])and computer science([11,12])over the past 40 years.
E.Rosen has proved characterization theorems on(locally)equivalent rewritability over finite Kripke models in [16].Characterization theorems over any class of Kripke models are proved by M.Otto in[14],where different versions of characterization theorems for MLI,ML plus a global modality and MLI plus a global modality are also proved.M.de Rijke proves characterization theorems for MLG in[15].Otto proves similar theorems forμML1The modal languageμML is ML plus a monadic least fixed point operator.in[13].A.Dawar and Otto proves several characterization theorems over kinds of classes of frames in[6].A model-theoretic characterization of MSO2MSO represents“monadic second-order”.toμML is proved by D.Janin and I.Walukiewicz in[9].G.Fontaine proves a model-theoretic characterization of MSO toμML over tree models in[7].Some theorems on globally equivalent rewritability of MLI to ML,MLG to ML,ML to EL3ML is the standard modal language;MLI is ML plus inverse modalities;MLG is ML plus graded modalities; MLGI is ML plus graded and inverse modalities; EL is a tractable modal language.For reference,see[17].over models are proved by F.Wolter in[17].
Equivalent rewritability is an important notion,but it is rather strict for it cannot introduce additional non-logical symbols.So it is necessary to introduce a weaker notion admitting additional non-logical symbols,i.e.,“conservative rewritability”,which aims at a conservative extension rather than an equivalent one.Conservative rewritability is often studied in description logics([1]).Some important theorems in this area are proved by[10]and[12].[7]resolves the global case of m-conservative(i.e.,model conservative)rewritability of MSO toμML over tree models.The locally m-conservative rewritability of MLG to ML over tree models can be inferred from some results in [7].[17]characterizes the global cases of s-conservative4S-conservative rewritability is another notion of conservative rewritability,being different from m-conservative rewritability.However,it is not studied in this paper.For reference,see[10].and mconservative rewritability of MLI to ML,MLG to ML and ML to EL over models.
Local equivalent and m-conservative rewritability over tree models are studied in this paper.Modal lauguages considered include ML,MLI,MLG and MLGI.Section 3 of this paper proves that each MLI-formula is equivalently rewritable into an MLformula at roots over tree models.Section 4 resolves whether each MLGI-formula is equivalently rewritable into an MLG-formula at roots over tree models.Section 5 characterizes the equivalent and m-conservative rewritability of“MLGI to MLI”over tree models.Section 6 resolves m-conservative rewritability of“MLGI to ML”over tree models.
2 Preliminaries
SyntaxML-formulas are formed according to the rule:
φ::=5represents ≥1.
wherepis a propositional variable.Other connectives are defined as follows:φ ∨ψ::=?(?φ ∧?ψ),::=p ∨?p,⊥::=,::=.
MLI is ML plus,6?represents ?≥1.MLG is ML plusand MLGI is ML plusand.It should be noticed that
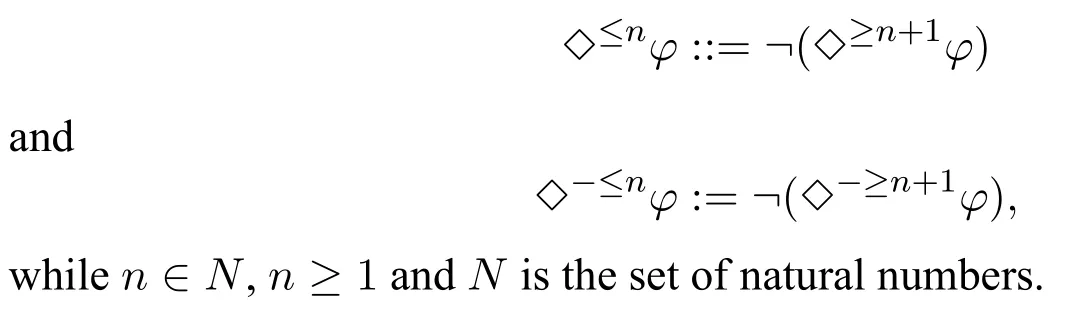
ModelA(Kripke)frame Fis a pair(W,R)and a(Kripke)model Mis a triple(W,R,V),whereWis a non-empty set of states,Ris a binary relation onWandVis a valuation.A pointed model is a pair(M,d),whereMis a model andd ∈W.
LetRrtbe the reflexive transitive closure ofR.If there is a uniqued?∈Wsuch thatd?Rrtdfor eachd ∈W,then the frame(W,R)is calledrootedandd?is its root.A rooted frame(W,R)withd?being its root is atreeif each stated ∈Wis reachable fromd?by a uniqueR-pathd?R···Rd.A model (W,R,V) is a tree model if its underlying frame(W,R)is a tree.
The truth-relations for ML-formulas(MLI-formulas,MLG-formulas and MLGIformulas)are defined in the familiar way for the atomic and boolean cases.The other cases are as follows:
? (M,d)|=iff(M,d′)|=αfor at leastndifferent pointsd′ ∈Wsuch thatdRd′;
? (M,d)|=iff(M,d′)|=αfor at leastndifferent pointsd′ ∈Wsuch thatd′Rd;
V(φ)is defined as{d ∈W:(M,d)|=φ}for each formulaφ.
RewritabilityLetLi(i ∈{1,2}) be a modal language.AnL1-formulaφislocally equivalently rewritableinto anL2-formula(or a set ofL2-formulas ??)over a class of modelsCif there is anL2-formulaψ(or a set ofL2-formulas ??)such that
? for each modelM=(W,R,V)∈Candd ∈W,(M,d)|=φiff(M,d)|=ψ(or(M,d)|=??).
AnL1-formulaφislocally m-conservatively rewritable7For reference,see[10].into anL2-formula(or a set ofL2-formulas ??)over a class of modelsCif there is anL2-formulaψ(or a set ofL2-formulas ??)such that
? for each modelM=(W,R,V)∈Candd ∈W,if(M,d)|=ψ(or(M,d)|=??),then(M,d)|=φ.
? for each modelM=(W,R,V)∈Candd ∈Wsuch that (M,d)|=φ,there is a modelM′ ∈Csuch thatM′=(W,R,V ′)andM=sig(φ)M′and(M′,d)|=ψ(or(M′,d)|=??).
HereM=sig(φ)M′means thatV(p)=V ′(p) for each propositional variablep ∈sig(φ)andsig(φ)represents the set of propositional variables occurring inφ.
According to the definition of locally m-conservative rewritability,the unique difference betweenMandM′is valuations of propositional variables,i.e.,M=M′iffV=V ′.Therefore,if anL1-formula is locally equivalently rewritable into anL2-formulaψ(or a set ofL2-formulas ??)over a class of modelsC,then it is locally m-conservatively rewritable into theL2-formulaψ(or the set ofL2-formulas ??)over the class of modelsC.
WhenCis the set of all Kripke models,“over a class of modelsC” is omitted.WhenC={(M,d?) :Mis a tree model andd?is its root},anL1-formulaφis said to be equivalently (or m-conservatively) rewritable into anL2-formula (or a set ofL2-formulas)at roots over tree models.
DegreeThe degree of an MLGI-formula is defined as follows:
?Deg(p)=0,
?Deg(⊥)=0,
?Deg(?φ)=Deg(φ),
?Deg(φ ∧ψ)=max{Deg(φ),Deg(ψ)},
?Deg()=Deg(φ)+1,
?Deg()=Deg(φ)+1.
The degree of an MLI-formula(or an MLG-formula)is defined similarly.
BisimulationLetM1=(W1,R1,V1)andM2=(W2,R2,V2)be two Kripke models.
A non-empty relationS ?W1×W2isa bisimulation8For reference,see[5].between(M1,d1)and(M2,d2)if the following conditions are satisfied:
? (d1,d2)∈S;
? if(u,v)∈S,uandvsatisfy the same propositional variables;
? if(u,v)∈SanduR1x1,there is anx2such thatvR2x2such that(x1,x2)∈S(the forth condition);
? if(u,v)∈SandvR2x2,there is anx1such thatuR1x1such that(x1,x2)∈S(the back condition).
A non-empty relationS ?W1× W2isan i-bisimulationbetween (M1,d1) and(M2,d2)ifSsatisfies all the conditions for bisimulation and the following conditions:
? if(u,v)∈Sandx1R1u,there is anx2such thatx2R2vsuch that(x1,x2)∈S(the inverse forth condition);
? if(u,v)∈Sandx2R2v,there is anx1such thatx1R1usuch that(x1,x2)∈S(the inverse back condition).
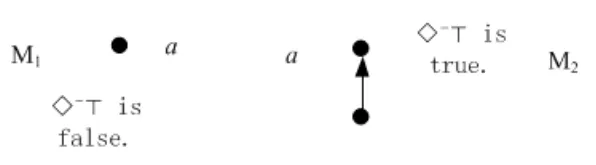
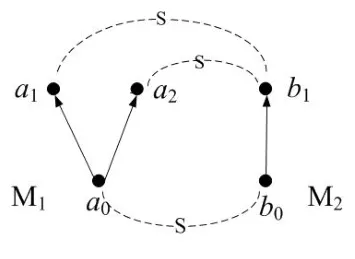
A non-empty relationS ?W1×W2isan n-bisimulationbetween(M1,d1)and(M2,d2)9For reference,see[5].if there is a sequence of relationsSn ?···?S0such that:S=and for each 0≤i ? (d1,d2)∈Sn; ? if(u,v)∈S0,uandvsatisfy the same propositional variables; ? if (u,v)∈ Si+1anduR1x1,there isx2such thatvR2x2and (x1,x2)∈Si(the forth condition); ? if (u,v)∈ Si+1andvR2x2,there isx1such thatuR1x1and (x1,x2)∈Si(the back condition). A non-empty relationS ?W1×W2isan n-i-bisimulationbetween(M1,d1)and (M2,d2) if there is a sequence of binary relationsSn ?··· ?S0such thatS=and it satisfies all the conditions forn-bisimulation and the following conditions,i.e.,for each 0≤i ? if (u,v)∈ Si+1andx1R1u,there isx2such thatx2R2vand (x1,x2)∈Si(the inverse forth condition); ? if (u,v)∈ Si+1andx2R2v,there isx1such thatx1R1uand (x1,x2)∈Si(the inverse back condition). van Benthem Characterization Theorem equivalently rewrites a first-order formula into an ML-formula by bisimulation.(See[2]and[3].) Theorem 1(van Benthem Characterization Theorem).A first-order formula A(x)is invariant under bisimulations iff it is locally equivalently rewritable into the standard translation of an ML-formula. A non-empty binary relationS ?W1×W2isa counting bisimulationbetween(M1,d1)and(M2,d2)if the following conditions are satisfied: ? (d1,d2)∈S; ? if(u,v)∈S,uandvsatisfy the same propositional variables; ? if(u,v)∈SandX1?u↑is finite10x↑={y ∈W :xRy}.,there is anX2?v↑such thatScontains a bijection betweenX1andX2(the forth condition); ? if(u,v)∈SandX2?v↑is finite,there is anX1?u↑such thatScontains a bijection betweenX1andX2(the back condition). A non-empty binary relationS ?W1×W2isan nm-counting bisimulation11If“m”is changed into“finite”,it is an n-counting bisimulation.between(M1,d1)and(M2,d2)if there is a sequence of binary relationsSn ?···?S0such thatS=Siand it satisfies the following conditions,i.e.,for each 0≤i ? (d1,d2)∈Sn; ? if(u,v)∈S0,uandvsatisfy the same propositional variables; ? if(u,v)∈Si+1,| X1|≤mandX1?u↑,there is anX2?v↑such thatSicontains a bijection betweenX1andX2(the forth condition); ? if(u,v)∈Si+1,| X2|≤mandX2?v↑,there is anX1?u↑such thatSicontains a bijection betweenX1andX2(the back condition). A non-empty binary relationS ?W1× W2is annm-ik-counting bisimulation12If“k”is changed into“finite”,it is an nm-i-counting bisimulation.If“m”and“k”are both changed into“finite”,it is an n-i-counting bisimulation.between(M1,d1)and(M2,d2)if there is a sequence of binary relationsSn ?··· ?S0such thatS=Siand it satisfies the conditions fornm-counting bisimulation and the following conditions,i.e.,for each 0≤i ? if(u,v)∈Si+1,|Y1|≤kandY1?u↓13x↓={y ∈W :yRx}.,then there is aY2?v↓such thatSicontains a bijection betweenY1andY2(the inverse forth condition); ? if(u,v)∈Si+1,| Y2|≤kandY2?v↓,then there is aY1?u↓such thatSicontains a bijection betweenY1andY2(the inverse back condition). Let us discuss these different but resembled bisimulations.According to their definitions,it is known that ? each counting bisimulation is also a bisimulation.However,the inverse does not hold,i.e.,not each bisimulation is a counting one. ? each(n-)i-bisimulation is also an(n-)bisimulation sinceionly means the extra conditions for predecessors.However,it is obvious that the inverse does not hold. ? eachnm-ik-counting bisimulation is also annm-counting bisimulation.The inverse does not hold. ? whenm=1,thenm-counting bisimulation becomes ann-bisimulation.It means that ann-bisimulation is in fact a special case ofnm-counting bisimulations whenm=1. ? whenm=1 andk=1,thenm-ik-counting bisimulation becomes ann-ibisimulation.In fact,ann-i-bisimulation is a special case ofnm-ik-counting bisimulation whenm=1 andk=1.It should be noticed that eachnm-ikcounting bisimulation between two tree models is in fact annm-i1-counting bisimulation since any point,except the root14The root of a tree model has no predecessor.,in a tree model has only one predecessor. Figure 1 gives an example of 22-i1-counting bisimulationS.LetM1=(W1,R1,V1)andM2=(W2,R2,V2)be two(tree)models showed in Figure 1 withV1(p)=V2(p)for each propositional variablep.Define a sequence of binary relationsS2?S1?S0as follows: S2={(a0,b0)} S1={(a0,b0),(a1,b2),(a2,b1),(a3,b2)} S0={(a0,b0),(a1,b2),(a2,b1),(a3,b2),(a4,b3),(a5,b4),(a6,b4)}. LetS=Si.It is easy to prove thatSis a 22-i1-counting bisimulation betweenM1andM2. Figure 1 Ap-morphismfrom(M1,d1)to(M2,d2)is a special bisimulationS15For reference,see[5].between(M1,d1)and(M2,d2)ifSis a surjective function fromW1toW2. Ani-p-morphismfrom (M1,d1) to (M2,d2) is a speciali-bisimulationSbetween(M1,d1)and(M2,d2)ifSis a surjective function fromW1toW2. Let Σ be a set of propositional variables.Each type of#-bisimulation is called a Σ-#-bisimulation,if no truth of propositional variables except those in Σ are considered. InvarianceAnL-formulaφisinvariant under#-bisimulations over a class of models C16#represents a type of bisimulation.,if (M1,d1)|=φiff(M2,d2)|=φ.17If it is substituted by“if(M1,d1) |= φ,then(M2,d2) |= φ”,then it means“preservation under#-bisimulations over a class of models C”. for each#-bisimulation between(M1,d1),(M2,d2)∈C. AnL-formulaφislocally preserved under inverse(i-)p-morphisms over a class of models Cif there is a(n)(i-)p-morphismffrom the pointed model(M1,d1)∈Cto the pointed model(M2,f(d1))∈Csuch that(M2,f(d1))|=φ,then(M1,d1)|=φ.WhenCis the class of all models,“over a class of modelsC”is omitted. This paper focuses on the class of all tree models.In some sections,the case thatC={(M,d?) :Mis a tree model andd?is its root}will be considered and it says to beinvariant(or preserved)under#-bisimulations at roots over tree models. Clearly invariance(or perservation)under bisimulations implies invariance(or perservation)undern-bisimulations for eachn ∈N.18For reference,see p.265 in[8]. The following theorem is proved in this section:“each MLI-formula is equivalently rewritable into an ML-formula at roots over tree models”.However,Lemma 1 has to be proved first. Lemma 1From each bisimulation between tree models with their roots being mapped to each other,ani-bisimulation is constructed between the same two tree models with their roots being mapped to each other. ProofLetM1=(W1,R1,V1) andM2=(W2,R2,V2) be two tree models withbeing their roots respectively.Assume thatSis a bisimulation between(M1,) and (M2,) with ()∈S.NowSi ?S(i ∈N) is defined as follows: Since eachSi ?S,S??S.For constructingS?,those pairs having no predecessor pairs that belong toSare deleted fromS. Assume that (d,e)∈S?anddR1d′.Then (d,e)∈Sifor somei ∈N.So(d,e)∈S.By the assumption thatSis a bisimulation between(M1,)and(M2,)with()∈S,there is a pointe′ ∈W2such thateR2e′and(d′,e′)∈S.By the definition ofS?,(d′,e′)∈Si+1and then(d′,e′)∈S?.That is,S?satisfies the forth condition.The back condition can be proved similarly.Now consider the inverse forth and inverse back conditions.SinceM1andM2are both tree models,each point except their roots has only one predecessor.If a pair inS?is not the root pair(),the inverse forth and back conditions hold by the definition ofS?.If a pair inS?is the root pair(),the inverse forth and back conditions also hold because the roots have no predecessors at all. □ Proposition 2 follows from Lemma 1 directly. Proposition 2From eachn-bisimulation between tree models with their roots being mapped to each other,ann-i-bisimulation is constructed between the same two tree models with their roots being mapped to each other. Proposition 3Each MLI-formulaφwithDeg(φ)≤nis invariant undern-i-bisimulations. ProofLetφbe an MLI-formula withDeg(φ)≤n.Assume that there is ann-ibisimulationS0with a sequenceSn ?··· ?S0between(M,w)and(M′,w′)and(w,w′)∈Sn.We should prove that We prove(1)by induction on the construction of MLI-formulas.The basis and boolean cases are trivial. Now consider the case thatφ=.Assume that (M,w)|=φ.Then there is a successorvofwinMsuch that (M,v)|=ψ.By the definition of ann-ibisimulation,there is a successorv′ofw′inM′such that(v,v′)∈Sn?1.So there is an(n ?1)-i-bisimulationS0withSn?1?···?S0between(M,v)and(M′,v′)and(v,v′)∈Sn?1.SinceDeg(ψ)≤n ?1,by induction hypothesis, (M,v)|=ψiff(M′,v′)|=ψ. By (M,v)|=ψ,we have that (M′,v′)|=ψ.Thus (M′,w′)|=φ.The inverse is proved similarly. Now consider the case thatφ=.Assume that(M,w)|=φ.Then there is a predecessorvofwinMsuch that (M,v)|=ψ.By the definition of ann-ibisimulation,there is a predecessorv′ofw′inM′such that (v,v′)∈Sn?1.Then there is an (n ?1)-i-bisimulationS0withSn?1?··· ?S0between (M,v) and(M′,v′)and(v,v′)∈Sn?1.SinceDeg(ψ)≤n ?1,by induction hypothesis, (M,v)|=ψiff(M′,v′)|=ψ. By (M,v)|=ψ,we have that (M′,v′)|=ψ.Thus (M′,w′)|=φ.The inverse is proved similarly. □ We introduce characteristic ML-formulasin[8]. Definition 4(Characteristic ML-Formula)Let Φ be a finite set of propositional variables and(M,d)be a pointed model withM=(W,R).The characteristic MLformula(n ∈N)is defined as follows: The main result of this section Theorem 5 is proved now. Theorem 5.Each MLI-formula is equivalently rewritable into an ML-formula at roots over tree models. ProofAssume thatφis an MLI-formula andDeg(φ)≤n.LetCbe the class of tree models(M,d?)withd?being its root such that(M,d?)|=φ.Assume that(M1,)∈Cand there is ann-bisimulationSbetween the tree model(M1,)and a tree model(M′,d′)withd′being its root such that(,d′)∈S.By Proposition 2,ann-i-bisimulationS?between(M1,)and(M′,d′)with(,d′)∈S?is constructed.Then by Proposition 3,(M1,)∈Cand(M1,)|=φ,we have that(M′,d′)|=φ.Therefore,(M′,d′)∈C.That is,Cis closed undern-bisimulations at roots over tree models.By Corollary 34 of[8]19Corollary 34 in[8]says that a class of pointed Kripke structures being closed under n-bisimulations is definable by an ML-formula in a finite vocabulary.,sinceCis closed undern-bisimulations,Cis definable by the ML-formula with Φ=sig(φ)20The ML-formula is finite as there are only finitely many suchof Definition 4.Therefore,the MLI-formulaφis equivalently rewritable into an ML-formula at roots over tree models. □ Proposition 6 follows directly from Theorem 5. Proposition 6Each MLI-formula is m-conservatively rewritable into an ML-formula at roots over tree models. However,is each MLI-formula equivalently rewritable into an ML-formulaat any pointover tree models? The answer is“No”,answered by Example 7.up to logical equivalence in the vocabularysig(φ)ofφ. Example 7Assume thatis equivalently rewritable into an ML-formulaψat each point over tree models,i.e., (M,d)|=iff(M,d)|=ψ for each tree model(M,d).Figure 2 says that(M1,a)and then(M1,a).The tree modelM1is a generated submodel ofM2in Figure 2.Sinceψis an MLformula,(M2,a).However,(M2,a)|=.Thusis not equivalently rewritable into an ML-formula at each point over tree models. Figure 2 For an MLGI-formulaφ,let Proposition 8Each MLGI-formulaφwithDeg(φ)≤n,Ind(φ)≤mandInd?(φ)≤kis invariant undernm-ik-counting bisimulations. ProofThis proposition is proved by induction on the construction of MLGI-formulasφwithDeg(φ)≤n,Ind(φ)≤mandInd?(φ)≤k.Assume that there is annm-ikcounting bisimulationSbetween(M,d)and(M′,d′).The basis and boolean cases are trivial. Now consider the case thatφ=.Assume that(M,d)|=φ.Then there are at leastldifferent successorsd1,···,dlofdinMsuch that (M,di)|=ψfor each 1≤i ≤l.By the definition of annm-ik-counting bisimulation,n ≥1 andl ≤m,there are at leastldifferent successorsofd′inM′such that(d1,),···,(dl,)∈S.Then there is an(n?1)m-ik-counting bisimulation?Sbetween(M,di)and(M′,)for each 1≤i ≤l.SinceDeg(ψ)≤n ?1,Ind(ψ)≤mandInd?(ψ)≤k,by induction hypothesis,(M,di)|=ψiff (M′,)|=ψfor each 1≤i ≤l.By(M,di)|=ψfor each 1≤i ≤l, for each 1≤i ≤l.Thus(M′,d′)|=φ.The inverse can be proved similarly. Now consider the case thatφ=.Assume that (M,d)|=φ.Then there are at leastldifferent predecessorsd1,···,dlofdinMsuch that(M,di)|=ψfor each 1≤i ≤l.By the definition of annm-ik-counting bisimulation,n ≥1 andl ≤k,there are at leastldifferent predecessorsofd′inM′such that(d1,),···,(dl,)∈S.Then there is an(n?1)m-ik-counting bisimulation?Sbetween(M,di)and(M′,)for each 1≤i ≤l.SinceDeg(ψ)≤n ?1,Ind(ψ)≤mandInd?(ψ)≤k,by induction hypothesis,(M,di)|=ψiff (M′,)|=ψfor each 1≤i ≤l.By(M,di)|=ψfor each 1≤i ≤l, for each 1≤i ≤l.Thus(M′,d′)|=φ.The inverse can be proved similarly. □ Proposition 9From eachnm-counting bisimulation between two tree models with their roots being mapped to each other,annm-ik-counting bisimulation (k ≥1) is constructed between these two tree models with their roots being mapped to each other. ProofLetM1=(W1,R1,V1)andM2=(W2,R2,V2)be two tree models withandbeing their roots respectively.Assume that Assume the contrary,i.e.,S′is not annm-i1-counting bisimulation.We can assume without loss of generality that there is a pair(1≤j ≤n)and a setD1?u′↑with|D1|≤m,but there is noD2?v′↑such thatS′contains a bijection betweenD1andD2.Sinceholds according to the definition ofS′.By the definition ofnm-counting bisimulation,there is a setD2?v′↑such thatScontains a bijection betweenD1andD2.According to the definition ofS′,S′contains a bijection betweenD1andD2,which is contrary to our assumption.So(1)holds.Since each point in a tree has only one predecessor,by the definition ofnm-ik-counting bisimulation,S′is anynm-ik-counting bisimulation for eachk ≥1 between(M1,)and(M2,)with their roots being mapped to each other. □ In order to prove the main theorem of this section Theorem 11,Theorem 4.11 of[15]is introduced first: Theorem 10 (Theorem4.11in [15]).Assume that the language of MLG contains finitely many propositional variables.Let K be a class of pointed models.Then K is definable by a single MLG-formula iff K is closed under nm-counting bisimulations for some n,m ∈N. Theorem 11.Each MLGI-formula is equivalently rewritable into an MLG-formula at roots over tree models. ProofGive an MLGI-formulaφwithDeg(φ)≤n,Ind(φ)≤mandInd?(φ)≤kforn,m,k ≥1.By Theorem 10,it needs to prove that each MLGI-formula is invariant undernm-counting bisimulations at roots over tree models.By Proposition 9,from eachnm-counting bisimulation between two tree models with their roots being mapped to each other,annm-ik-counting bisimulation is constructed between these two tree models with their roots being mapped to each other.By Proposition 8,it can be easily proved that each MLGI-formulaφis invariant undernm-counting bisimulations at roots over tree models. □ The following proposition follows directly from Theorem 11. Proposition 12Each MLGI-formula is m-conservatively rewritable into an MLGformula at roots over tree models. However,not each MLGI-formula is locally equivalently rewritable into an MLGformula at any point over tree models.Our example is stillin Example 7.is also an MLGI-formula.Since each MLG-formula is invariant under counting bisimulations at any point over tree models21For reference,see Proposition 3.3 in [15],which says that each MLG-formula is invariant under counting bisimulations.,ifcan be locally equivalently rewritable into an MLG-formula,it should be invariant under counting bisimulations at any point over tree models.Now Figure 2 shows that it is not the truth,for(M2,a)|=,(M1,a)and there is a counting bisimulationS={(a,a)}between the two tree models(M1,a)and(M2,a). Instead,the following theorem can be proved from Proposition 3.3 in[15],Theorem 10(i.e.,Theorem 4.11 in[15])and a similar proof of Theorem 17.22We should add“counting”before the word“bisimulations”in Theorem 17 and a quite similar theorem to Theorem 17 can be proved by a similar way of Theorem 17. Theorem 13.Let φ be an MLGI-formula with Deg(φ)≤n.Then the following conditions are equivalent: (i) φ is locally equivalently rewritable into an MLG-formula over tree models; (ii) φ is locally preserved(or invariant)under n-counting bisimulations over tree models; (iii) φ is locally preserved (or invariant) under counting bisimulations over tree models. Definition 14 (Height of States in Rooted Models)LetM=(W,R,V) be a rooted model with the rootd?.The heightH(d?) of the rootd?ofMis 0; if the heightH(d) ofdinMisn(n ∈N),then for each immediate successor23A successor y of x is an immediate successor of x ifx= y,?yRx and xRzRy implies z= x or z=y for each z ∈W.d′ofdinM,the heightH(d′)ofd′inMthat has not been assigned a height smaller thann+1 isn+1.The heightH(M)of a rooted modelMisnif the maximum height of points inMisn.Otherwise,H(M)is infinite. Definition 15 (Submodel of M Induced by X)The submodelM|Xof a modelM=(W,R,V) induced byX ?Wis defined asM|X=(X,R|X,V|X),whereR|X=R ∩(X ×X)andV|X=V(p)∩Xfor each propositional variablep. Proposition 16LetM=(W,R,V),d ∈WandX={e ∈W:H(e)≤max{H(d′) :d′ ∈Xd,n}},whereXd,n=d↑0∪··· ∪d↑n.Then there are ann-bisimulation and ann-i-bisimulation between(M|X,d)and(M,d). ProofA sequence of binary relationsSn ?···?S0is defined as follows(1≤i ≤n): It is easy to prove that(M|X,d)and(M,d)is bothn-bisimular andn-i-bisimular.□ The following theorem holds for MLGI-formulas,also for MLG-formulas and MLI-formulas. Theorem 17.Let φ be an MLGI-formula with Deg(φ)≤n.The following two conditions are equivalent: (i) φ is locally preserved(or invariant)under n-bisimulations over tree models; (ii) φ is locally preserved(or invariant)under bisimulations over tree models. ProofWe only need to prove(?).Assume that an MLGI-formulaφwithDeg(φ)≤nis locally preserved24The“invariant”-case can be proved similarly.undern-bisimulations over tree models.LetM1=(W1,R1,V1)andM2=(W2,R2,V2)be two tree models,Sbe a bisimulation between(M1,d)and (M2,e) and (M1,d)|=φ.By Proposition 16,there is ann-bisimulation between (,d) and (M1,d),whereX1={d′′ ∈W1:H(d′′)≤max{H(d′) :d′ ∈}}and=d↑0∪···∪d↑n.Sinceφis locally preserved undernbisimulations over tree models,by (M1,d)|=φ,we have that (,d)|=φ.Similarly,there is ann-bisimulation between(,e)and(M2,e),whereX2={e′′ ∈W2:H(e′′)≤max{H(e′):e′ ∈}}and=e↑0∪···∪e↑n.Define a sequence of binary relationsSn ?Sn?1···?S0as follows(1≤i ≤n): Since(d,e)∈S,S??S.Then it is easy to prove thatS?is ann-bisimulation between(,d)and(,e).By our assumption thatφis locally preserved undern-bisimulations over tree models,from(,d)|=φwe have that(,e)|=φ.Since there is ann-bisimulation between(,e)and(M2,e),(M2,e)|=φ.Therefore,φis locally preserved under bisimulations over tree models. □ Not each MLGI-formula is equivalently rewritable into an MLI-formula at roots over tree models.For example,2.Assume that2is equivalently rewritable into an MLI-formula at roots over tree models.Since each MLI-formula is invariant underi-bisimulations at roots over tree models,2should be invariant underibisimulations at roots over tree models.However,it is not the truth.We show it as follows. LetM1=(W1,R1,V1) andM2=(W2,R2,V2) be the two tree models in Figure 3 respectively.HereV1(p)=V2(p)=?for each propositional variablep.It is obvious that(M1,a0)|=2,(M2,b0)2,but there is ani-bisimulationS={(a0,b0),(a1,b1),(a2,b1)}between the two tree models(M1,a0)and(M2,b0). The following theorem is proved,instead. Figure 3 Theorem 18.Let φ be an MLGI-formula with Deg(φ)≤n.Then the following conditions are equivalent: (i) φ is equivalently rewritable into an MLI-formula at roots over tree models; (ii) φ is preserved(or invariant)under bisimulations at roots over tree models; (iii) φ is preserved(or invariant)under n-bisimulations at roots over tree models; (iv) φ is preserved(or invariant)under n-i-bisimulations at roots over tree models; (v) φ is preserved(or invariant)under i-bisimulations at roots over tree models. Proof2?3 can be proved by a very similar proof of Theorem 17. 3?4 is prove as follows:3?4 follows directly from the fact that eachn-i-bisimulation is also ann-bisimulation by the definitions ofn-bisimulation andn-i-bisimulation.4?3 follows from Proposition 2. 2?5 is proved as follows:2?5 follows directly from the fact that eachibisimulation is also a bisimulation by the definitions of bisimulation andi-bisimulation.5?2 follows from Lemma 1. Now we prove that 1?5.(1?5)Assume that an MLGI-formulaφis equivalently rewritable into an MLI-formulaψat roots over tree models.Since each MLIformula is preserved(or invariant)underi-bisimulations at roots over tree models,φis preserved(or invariant)underi-bisimulations at roots over tree models.(5?1)Assume thatφis an MLGI-formula withDeg(φ)≤nand is preserved (or invariant) underi-bisimulations at roots over tree models.There are only finitely many non-equivalent MLI-formulasβwithDeg(β)≤mandsig(β)?sig(φ) for eachm ∈N.For each tree modelM=(W,R,V) andd ∈W,let the MLI-formulabe the conjunction of all these finitely many non-equivalent MLI-formulasβwithDeg(β)≤m,sig(β)?sig(φ)and(M,d)|=β.Now let whereMis a tree model withdbeing its root such that(M,d)|=φ.Being a disjunction of finitely many non-equivalent MLI-formulas,αis a proper MLI-formula. Now we prove thatφis equivalently rewritable into the MLI-formulaαat roots over tree models.LetM?be a tree model andd?be its root.Assume that(M?,d?)|=φ.By the definition ofαand,it is clear that(M?,d?)|=and then(M?,d?)|=α. Now assume thatM?=(W?,R?,V ?) is a tree model,d?is the root ofM?and(M?,d?)|=α.Then there is a tree modelM′=(W′,R′,V ′)withd′being its root and(M′,d′)|=φsuch that(M?,d?)|=.Now we prove the following claim: ? There is ann-i-bisimulationSbetween(M′,d′)and(M?,d?)with(d′,d?)∈S. Since(M?,d?)|=,it is easy to prove that(M?,d?)|=δiff(M′,d′)|=δfor each MLI-formulaδwithDeg(δ)≤nandsig(δ)?sig(φ). Assume thatd?R?v.By(M?,v)|=and then(M?,d?)|=.From (M?,d?)|=,we have that (M?,d?)|=δiff (M′,d′)|=δfor each MLI-formulaδwithDeg(δ)≤nandsig(δ)?sig(φ).So (M′,d′)|=.Thus there is a pointv′ ∈W′such thatd′R′v′and (M′,v′)|=.Then for each MLI-formulaδwithDeg(δ)≤n ?1 andsig(δ)?sig(φ),(M?,v)|=δiff(M′,v′)|=δ.By a similar argument,we can also prove that ifd′R′v′,there is a pointv ∈W?such thatd?R?vand for each MLI-formulaδwithDeg(δ)≤n ?1 andsig(δ)?sig(φ),(M?,v)|=δiff(M′,v′)|=δ. Now letSn?1be the union ofSn={(d′,d?)}and the set of all the above selected pairs(v′,v)such thatd′R′v′,d?R?vand(M?,v)|=δiff(M′,v′)|=δfor each MLIformulaδwithDeg(δ)≤n ?1 andsig(δ)?sig(φ).Similarly,a sequence of binary relationsSn ?Sn?1?···?S0is defined as follows: for each 1≤i ≤n,Si?1is the union ofSiand the set of all the selected pairs(v′,v) satisfying thatw′R′v′,wR?vfor some (w′,w)∈Siand (M?,v)|=δiff(M′,v′)|=δfor each MLI-formulaδwithDeg(δ)≤i ?1 andsig(δ)?sig(φ).It is easy to prove that is ann-i-bisimulation between(M′,d′)and(M?,d?)with(d′,d?)∈S0. Sinceφis preserved(or invariant)underi-bisimulations at roots over tree models,by 2?5,2?3 and 3?4,φis preserved(or invariant)undern-i-bisimulations at roots over tree models.Then by(M′,d′)|=φ,we have that(M?,d?)|=φ. □ If being preserved(or invariant)at each point of a tree model is considered,we have the following theorem: Theorem 19.Let φ be an MLGI-formula with Deg(φ)≤n.Then the following conditions are equivalent: (i) φ is locally equivalently rewritable into an MLI-formula over tree models; (ii) φ is locally preserved(or invariant)under n-i-bisimulations over tree models; (iii) φ is locally preserved(or invariant)under i-bisimulations over tree models. Proof2?3 can be proved by a similar argument to the proof of Theorem 17.3?1 follows from a similar argument to the proof of 1?5 of Theorem 18. □ Lemma 2 follows from the fact that eachi-p-morphism is ani-bisimulation by their definitions and the fact that each MLI-formula is preserved(or invariant)underi-bisimulations. Lemma 2Let ?be a set of propositional variables,fbe a ?-i-p-morphism fromM1toM2.Then (M1,d)|=φiff (M2,f(d))|=φfor each MLI-formulaφwithsig(φ)??. We prove Theorem 20 by Lemma 2. Theorem 20.Let φ be an MLGI-formula,??be a set of MLI-formulas and?be a set of propositional variables such that sig(φ)??and sig(α)??for each MLIformula α ∈??.If φ is locally m-conservatively rewritable into??,then it is locally preserved under inverse?-i-p-morphisms. ProofLetφbe an MLGI-formula,??be a set of MLI-formulas and ?be a set of propositional variables such thatsig(φ)??andsig(α)??for each MLI-formulaα ∈??.Assume thatφis locally m-conservatively rewritable into ??and there is a?-i-p-morphismffrom a modelM1=(W1,R1,V1)to a modelM2=(W2,R2,V2)withd1∈W1,d2∈W2,f(d1)=d2and (M2,d2)|=φ.We need to prove that(M1,d1)|=φ.According to our assumption that(M2,d2)|=φand the definition of locally m-conservative rewritability,there is a pointed model(,d2)with=(W2,R2,)such that(,d2)|=??andM2=sig(φ).ByM2=sig(φ),we have that By the definition of locally m-conservative rewritability,(M,d)|=??implies(M,d)|=φfor each pointed model(M,d),then by(,d1)|=??we have that Give an MLGI-formulaφwithDeg(φ)≤?.Let Σ?(φ) be the set of all subformulas ofφ.Take new propositional variablesfor each subformla,and let Σ be the union ofsig(φ) and the set of all the new propositional variables.For eachχ ∈Σ?(φ),letχ?be the MLI-formula obtained fromχby replacing all the topmost subformulaswithpψand⊥respectively.is defined as the set of the MLI-formulaφ?and the following infinite many formulas for each: while eachψi(1≤i ≤n)is an MLI-formula withsig(ψi)?Σ and2irepresents a sequence ofioperators2(i ∈N). Now we can prove the main result Theorem 21 of this subsection. Theorem 21.Let φ be an MLGI-formula,??be a set of MLI-formulas and?be a set of propositional variables such that sig(φ)??and sig(α)??for each MLIformula α ∈??.Then the MLGI-formula φ is locally m-conservatively rewritable into??over tree models iff φ is locally preserved under inverse?-i-p-morphisms over tree models. Proof(?)It follows directly from Theorem 20.(?)Letφbe an MLGI-formula,Σ?(φ)be the set of all subformulas ofφ,Σ besig(φ)together with all the fresh propositional variablesbe the set of MLI-formulas being defined above.Assume that the MLGI-formulaφwithDeg(φ)≤?is locally preserved under inverse ?-i-p-morphisms over tree models withsig(φ)??andsig(α)??for each MLI-formulaα ∈.We prove thatφcan be locally m-conservatively rewritable into the setof MLI-formulas over tree models.We need to prove that Claim 1 for each tree modelM=(W,R,V)andd ∈Wsuch that(M,d)|=φ,there is a tree modelM′=(W,R,V ′)such thatM=sig(φ)M′and(M′,d)|=; Claim 2 for each tree modelM=(W,R,V) andd ∈W,if (M,d)|=,then(M,d)|=φ. To prove Claim 1,we should notice that each point in a tree model has only one predecessor,and then each MLGI-formula(n ≥2)is equivalent to⊥at each point of a tree model.Assume thatM=(W,R,V) is a tree model,d ∈Wand(M,d)|=φ.Let Then a new modelM′=(W,R,V ′) is constructed fromM.It is obvious thatM=sig(φ)M′and(M′,d)|=. Let’s consider Claim 2.Give a tree modelM=(W,R,V)withd ∈Wandd?being its root.Assume that(M,d)|=and(M,d)φ.LetS0={d′ ∈W:?k ∈N(d′ ∈d↓k)}.25d↓k= {d′ ∈W : ?d1···dk?1 ∈W(d′Rdk?1···d2Rd1Rd)} for k ∈N.When k=0,d↓0=syggg00.We should notice that the root of M belongs to S0,i.e.,d?∈S0.Assume thatS0?S1··· ?Snhave already been defined.Fix a pointe ∈Sn. Step(ii) For eachψ=∈Σ?(φ) (m ≥2) such that (M,e)|=pψ,selectmpointse1,···,em ∈Wsuch thateReiand for each 1≤i ≤m. Step(iii) For each subformulaofφ?such that(M,e)|=,select a pointe′ ∈Wsuch thateRe′and (M,e′)|=γ.For each subformulaofφ?such that(M,e)|=,select the only predecessore′ ∈Wofesuch that(M,e′)|=γ. Step(iv) For each subformulaofψ′?with∈Σ?(φ) (n ≥2) such that(M,e)|=,select a pointe′ ∈ Wsuch thateRe′and (M,e′)|=γ.For each subformulaofψ′?with∈Σ?(φ) (n ≥2) such that(M,e)|=,select the only predecessore′ ∈Wofesuch that(M,e′)|=γ. Repeat the above selection process for each pointe ∈Sn.LetSn+1contains all these pointseiore′selected by the above selection process(i)–(iv).Next,for each twod1,d2∈Snsuch thatd1is Σ-i-bisimilar tod2inM28Each point is Σ-i-bisimilar to itself in M.Therefore,if d1=d2,then d1 is definitely Σ-i-bisimilar to d2 in M.,ifand∈Sn+1,then each successor(or the only predecessor)ofd2being Σ-i-bisimilar toinMshould be added intoSn+1.LetSn+1be the smallest set of points satisfying all of the above conditions.Then the sequence of sets of pointsS0?S1···?Sn···is defined completely. The selection process (i)–(iv) may choose two successors of one point which are equivalent over MLI-formulasαwithsig(α)?Σ inMbut not Σ-i-bisimilar to each other inM.Assume that such a case occurs,i.e.,there are two successorsd1,d2∈Si+1ofd′ ∈Si(i ∈N)such thatd1,d2are equivalent over MLI-formulasαwithsig(α)?Σ inMbutd1is not Σ-i-bisimilar tod2inM.Let We delete the points of the setsfrom eachSi(i ∈N)for each two pointsd1,d2∈W.Let(i ∈N)be the remaining set of points after the above deletion process.Then a new sequenceis constructed from the sequenceS0?S1···?Sn···. Now a new modelM′=(W′,R′,V ′)can be defined as follows: According to the assumption thatMis a tree model withd?being its root,M′is also a tree model withd?being its root.29We should notice that d?∈S0 and d?won’t be deleted from each Si(i ∈N)since it is the root of M.So d?∈W′.Then by(M,d)φ,we have that(M′,d)φ.We need to prove that(M′,d)|=.Since we have Step(ii),the only cases inneeded to be considered are the formulas while eachψi(1≤i ≤nandn ≥2)is an MLI-formula withsig(ψi)?Σ. Assume the contrary,i.e.,there are a pointd′ ∈d↑m ?W′(0≤m ≤?)and MLI-formulasψ1,···,ψn(n ≥2) withsig(ψi)?Σ (1≤i ≤n) such that(M′,d′)pψfor someψ=∈Σ?(φ)and It means thatd′hasndifferentR′-successors that are not equivalent over MLIformulasαwithsig(α)?Σ inM′,and then not Σ-i-bisimilar to each other inM′.By the construction ofM′,ifd1∈W′is Σ-i-bisimilar tod2∈W′inM,thend1is Σi-bisimilar tod2inM′.Sod′hasndifferentR-successors that are not Σ-i-bisimilar to each other inM.We prove that thendifferentR-successors ofd′are also not equivalent over MLI-formulasαwithsig(α)?Σ inM. Assume the contrary,i.e.,there are two successors∈W′and∈W′ofd′ ∈W′satisfying thatare not equivalent over MLI-formulasαwithsig(α)?Σ inM′and not Σ-i-bisimilar to each other inM,but they are equivalent over MLI-formulasαwithsig(α)?Σ inM.Since Σ is finite30If Σ is finite,there are only finitely many non-equivalent MLI-formulas α with sig(α) ?Σ and Deg(α)≤2?.andare equivalent over MLI-formulasαwithsig(α)?Σ inM,is Σ-2?-i-bisimilar toinM.31The proof of this part is similar to Proposition 2.31 of[5].According to the construction of the sequenceis Σ-i-bisimilar toinM′.Therefore,is equivalent toover MLI-formulasαwithsig(α)?Σ inM′,which is contrary to our assumption thatare not equivalent over MLI-formulasαwithsig(α)?Σ inM′.Sod′ ∈d↑m(0≤m ≤?) hasndifferentR-successors that are not equivalent over MLI-formulasαwithsig(α)?Σ to each other inM. Since thesendifferentR-successors ofd′32These n points are also R′-successors of d′.satisfyψ′?inM′,according to the construction ofM′,each of them also satisfiesψ′?inM.Then there are MLI-formulaswithsig()?Σ(1≤i ≤n)such that Last,from(M,d)|=,d′ ∈d↑m(0≤m ≤?)?W′ ?Wand(0?),we have that(M,d′)|=pψ.It means that(M′,d′)|=pψby the construction ofM′,which is contrary to our assumption that(M′,d′)pψ.Therefore,(M′,d)|=is proved. Since“being Σ-i-bisimilar to”is an equivalence relation,let[e]={e′ ∈W′:(M′,e)is Σ-i-bisimilar to(M′,e′)}fore ∈W′.A new modelM′′=(W′′,R′′,V ′′)can be defined fromM′as follows: W′′={[e]:e ∈W′}, [d1]R′′[d2]iff there aree1∈[d1]ande2∈[d2]such thate1R′e2. V ′′(p)={[e]∈W′′:e ∈V ′(p)}for each propositional variablep ∈Σ. According to the construction ofM′andM′′,M′′is of finite outdegrees,i.e.,each point inM′′has only finitely many successors. Now we show thatf:[e]fore ∈W′and[e]∈W′′is a Σ-i-p-morphism fromM′toM′′.The valuation and the forth conditions are obviously satisfied by the definition ofM′′.We prove the back condition as follows: The inverse forth condition follows from the definition ofR′′.Now we prove the inverse back condition as follows: Therefore,f:e[e]fore ∈W′and[e]∈W′′is a Σ-i-p-morphism fromM′toM′′. We prove thatM′′is a tree model.SinceM′is a tree model withd?being its root,there is anR′′-path from[d?]to[e]for each[e]∈W′′.If[d?]33[d?]={d?}.has a predecessor inM′′,d?has a predecessor inM′according to the definition ofR′′,which is contrary to our assumption thatd?is the root of the tree modelM′.Therefore,[d?]is the root ofM′′.Now we prove that there is a unique path from [d?]to [e]for each [e]inM′′.Assume the contrary,i.e.,there is a[e]inM′′such that[e]has two different predecessors[d1]and[d2]inM′′.Sincefis a Σ-i-p-morphism fromM′toM′′,there are two points∈[d1]and∈[d2]such that.Since[d1][d2],is also different from.It means that the pointehas two different predecessors in the tree modelM′,which is contrary to the definition of a tree model.So there is only one unique path from[d?]to[e]for each[e]inM′′.Therefore,M′′is a tree model with[d?]being its root. Next we prove the following claims: Claim(1) (M′′,[d])|=; Claim(2) Let[u]and[v]be successors of a point[w]∈W′′inM′′.For each MLI-formulaαwithsig(α)?Σ,if (M′′,[u])|=αiff (M′′,[v])|=α,then[u]=[v]; Claim(1) (M′′,[d])|=φ. Claim(1)follows directly from Lemma 2 and(M′,d)|=.34We have proved that there is a Σ-i-p-morphism from M′ to M′′Claim(2)is proved as follows: Let[u]and[v]be successors of a point[w]∈W′′inM′′.Assume that for each MLI-formulaαwithsig(α)?Σ.SinceM′′is of finite outdegrees,[u]is Σ-i-bisimilar to[v]inM′′.35Since[u]and[v]has the same unique predecessor[w]in M′′,the proof of this part is similar to the proof of Theorem 2.24(i.e.,Hennessy-Milner Theorem)in[5].Since[u],[v]are successors of the point[w]inM′′and there is a Σ-i-p-morphism fromM′toM′′,there are pointsu1∈[u1]=[u]andv1∈[v1]=[v]such thatwR′u1andwR′v1.According to Lemma 2 and the fact thatf:e[e]fore ∈W′and[e]∈W′′is a Σ-i-p-morphism fromM′toM′′, for each MLI-formulaαwithsig(α)?Σ.Then by(1?),we have that for each MLI-formulaαwithsig(α)?Σ. Now we prove thatu1is Σ-i-bisimilar tov1inM′.Assume the contrary,i.e.,u1is not Σ-i-bisimilar tov1inM′.Sinceu1andv1has the same uniqueR′-predecessorwin the tree modelM′,we can assume without loss of generality that there is a point∈W′such thatand no successor ofv1is equivalent toover MLI-formulasαwithsig(α)?Σ inM′.Fromand the fact that there is a Σ-i-p-morphism fromM′toM′′,and thenby[u]=[u1].Since[u]is Σ-i-bisimilar to[v]inM′′,there is a point[v′]∈W′′such that[v]R′′[v′]andis Σ-i-bisimilar to[v′]inM′′.Then for each MLI-formulaαwithsig(α)?Σ.By Lemma 2 and the fact that there is a Σ-i-p-morphism fromM′toM′′, for each MLI-formulaαwithsig(α)?Σ.Thus,by(2?),we have that for each MLI-formulaαwithsig(α)?Σ.From[v]R′′[v′]and[v1]=[v],[v1]R′′[v′]holds.By the fact that there is a Σ-i-p-morphism fromM′toM′′,there is a point∈W′such thatand=[v′].Then from∈[v′]we get that for each MLI-formulaαwithsig(α)?Σ.Therefore,by(3?)and(4?), for each MLI-formulaαwithsig(α)?Σ.However,(5?)is contrary to our assumption that no successors ofv1is equivalent toover MLI-formulasαwithsig(α)?Σ inM′.Thusu1is Σ-i-bisimilar tov1inM′. Sinceu1is Σ-i-bisimilar tov1inM′,then [u1]=[v1].By [u1]=[u]and[v1]=[v],we finally get that[u]=[v].That is,Claim(2)is proved. We prove Claim(3)by showing that for eachψ=∈Σ?(φ) (n ≥2) and for each [d′]∈[d]↑0∪[d]↑1∪···∪[d]↑??Deg(ψ). SinceM′′is a tree model,we should notice that for each[e]∈W′′and for eachγ=∈Σ?(φ)(n ≥2).So we can assume without loss of generality that there are no such subformulasγ=(n ≥2) occurring in eachψ=∈Σ?(φ).36If such a subformula γ=?≥nγ′ (n ≥2)occurs in ψ,we can substitute γ with ⊥immediately.We prove (6?) by induction on the numbers of subformulas(t ≥2) occurring inψ′forψ=∈Σ?(φ)(n ≥2).Letψ=∈Σ?(φ) (n ≥2) andkbe the number of subformulas(t ≥2)occurring inψ′. Assume thatk=0.Thenψ′=ψ′?.Let[d′]∈[d]↑0∪[d]↑1∪···∪[d]↑??Deg(ψ).Assume that(M′′,[d′])|=pψ.By Claim(1)that(M′′,[d])|=and[d′]∈[d]↑0∪[d]↑1∪···∪[d]↑??Deg(ψ),we have that Assume that(M′′,[d′])|=ψ.Then[d′]hasndifferent successorssuch that(M′′,)|=ψ′(n ≥2)for each 1≤i ≤n.None ofis equivalent to another over MLI-formulasαwithsig(α)?Σ according to Claim(2).Therefore,there arendifferent MLI-formulasψ1,···,ψnwithsig(ψi)?Σ such that Fromψ′=ψ′?,we get that(M′′,[d′])|=pψ.That is,(6?)holds fork=0. Now assume that (6?) holds fork ≤m ∈N.Let’s consider the case thatk=m+1.Let[d′]∈[d]↑0∪[d]↑1∪···∪[d]↑??Deg(ψ).Let(q ∈N)be the topmost subformulas having the form(n ≥2)occurring inψ′.Letkibe the number of subformulas(n ≥2) occurring inδifor each 1≤i ≤q.By induction hypothesis that(6?)holds fork ≤mand the fact that eachki ≤k ≤mfor 1≤i ≤q,we have that Last,from (6?),Claim (1) andφ?∈,Claim (3) that (M′′,[d])|=φis proved. Sinceφis locally preserved under inverse ?-i-p-morphisms over tree models such thatsig(φ)??andsig(α)??for each MLI-formulaα ∈,from Claim(3)and the fact that there is a Σ-i-p-morphism fromM′toM′′,we have that(M′,d)|=φ,which is contrary to what we have prove that(M′,d)φ.Therefore,for each tree modelM=(W,R,V)withd ∈W,if(M,d)|=,then(M,d)|=φ,i.e.,Claim 2 is proved. □ Now we consider the problem of locally m-conservative rewritability of MLGI to ML over tree models. Theorem 22,the main result of this subsection,can be proved by Theorem 21. Theorem 22.Let φ be an MLGI-formula,??be a set of ML-formulas and?be a set of propositional variables such that sig(φ)??and sig(α)??for each MLformula α ∈??.Then the MLGI-formula φ is locally m-conservatively rewritable into??over tree models iff φ is locally preserved under inverse?-p-morphisms over tree models. Proof(?) This part can be proved by a similar one to the proof of Theorem 20.(?) Letφbe an MLGI-formula,??be a set of ML-formulas and ?be a set of propositional variables such thatsig(φ)??andsig(α)??for each ML-formulaα ∈??.Assume that an MLGI-formulaφis locally preserved under inverse ?-pmorphisms over tree models.Since eachi-p-morphism is also ap-morphism,φis locally preserved under inversei-p-morphisms over tree models.By Theorem 21 and the fact that each ML-formula is also an MLI-formula,φis locally m-conservatively rewritable into ??over tree models. □ Lemma 3 says,ap-morphism between two tree modelsfitself is also ani-pmorphism. Lemma 3LetM1andM2be tree models.Then eachp-morphism fromM1toM2is also ani-p-morphism fromM1toM2. ProofAssume thatM1andM2are tree models withbeing their roots respectively.Letfbe ap-morphism fromM1toM2.We prove thatfis also ani-p-morphism fromM1andM2.Assume the contrary,i.e.,fis not ani-p-morphism fromM1toM2.It means thatf(x)R2f(y) withx,y ∈W1but there is no pointz ∈W1such thatzR1yandf(z)=f(x).SinceM1andM2are tree models andby the definition ofp-morphisms,.Then there is anR1-path···R1xnR1yfromtoyinM1.Thus,according to the definition ofp-morphisms,there is anR2-pathR2f(x1)R2f(x2)R2···R2f(xn)R2f(y) fromtof(y)inM2.Since there is no pointz ∈W1such thatzR1yandf(z)=f(x),we have thatf(xn)f(x).Then the pointf(y) inM2has two different predecessorsf(x) andf(xn).It is contrary to our assumption thatM2is a tree model.Therefore,fitself is also ani-p-morphism fromM1andM2. □ From Theorem 22 and Lemma 3,the following theorem is got immediately,whose proof is omitted for its clearness. Theorem 23.Let φ be an MLGI-formula,??be a set of ML-formulas and?be a set of propositional variables such that sig(φ)??and sig(α)??for each MLformula α ∈??.The following conditions are equivalent for the MLGI-formula φ: (i) φ is locally m-conservatively rewritable into??over tree models; (ii) φ is locally preserved under inverse?-p-morphisms over tree models; (iii) φ is locally preserved under inverse?-i-p-morphisms over tree models.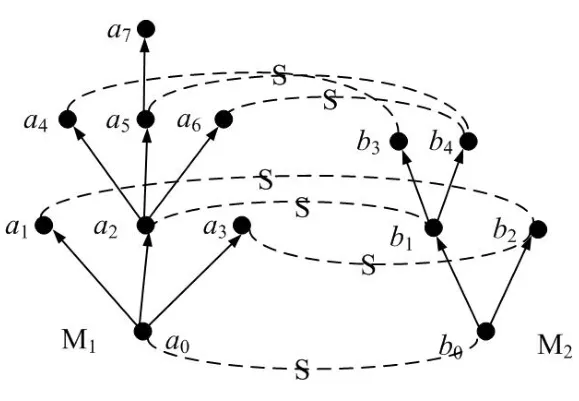
3 MLI to ML
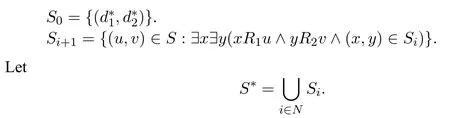
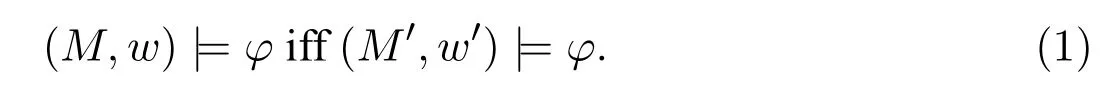
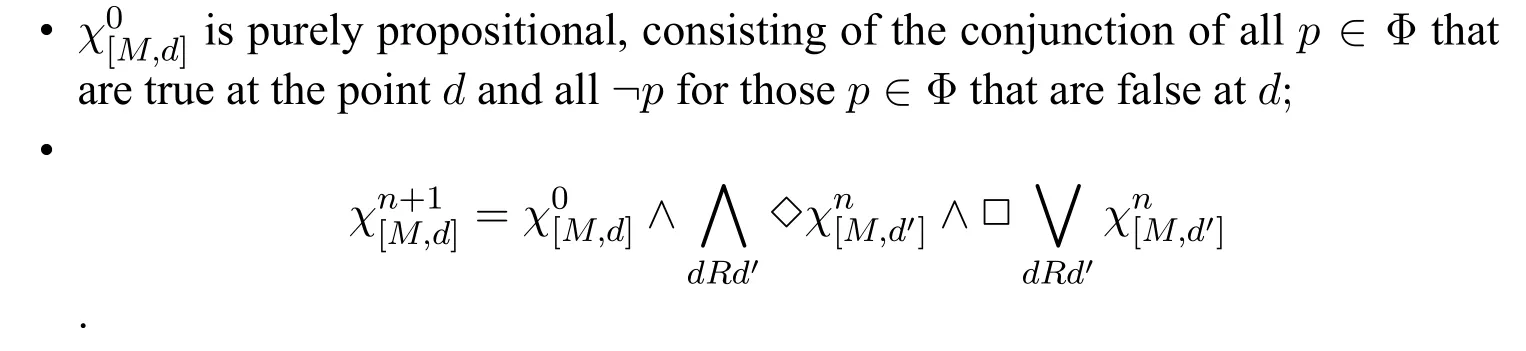
4 MLGI to MLG
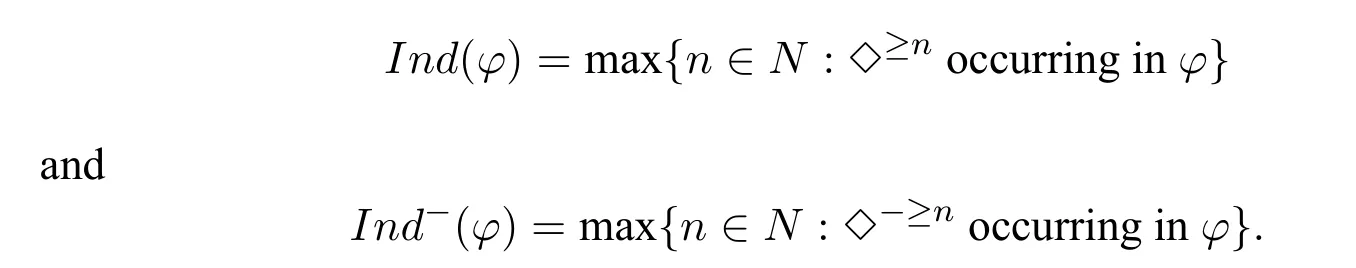
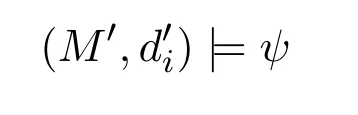
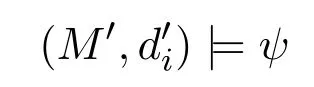

5 MLGI to MLI
5.1 Equivalent rewritability of MLGI to MLI
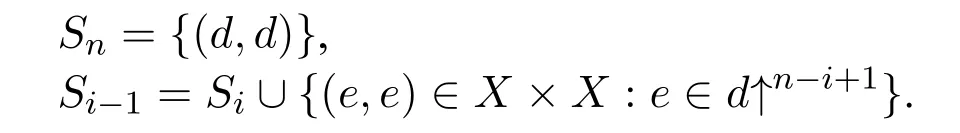
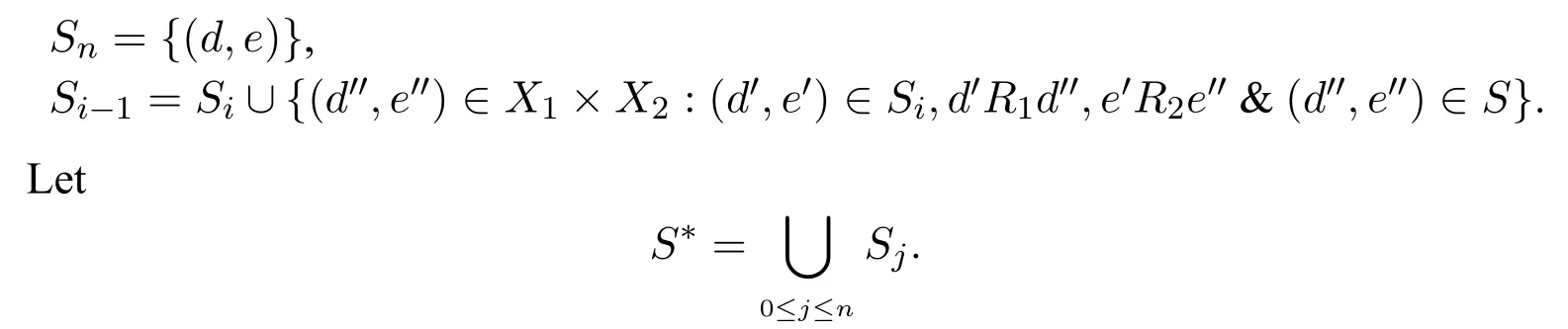
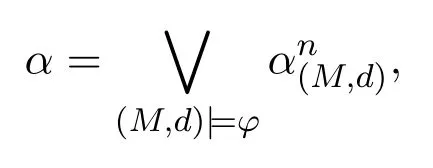
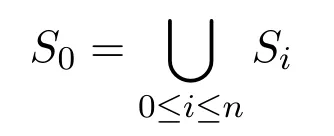
5.2 m-Conservative rewritability of MLGI to MLI
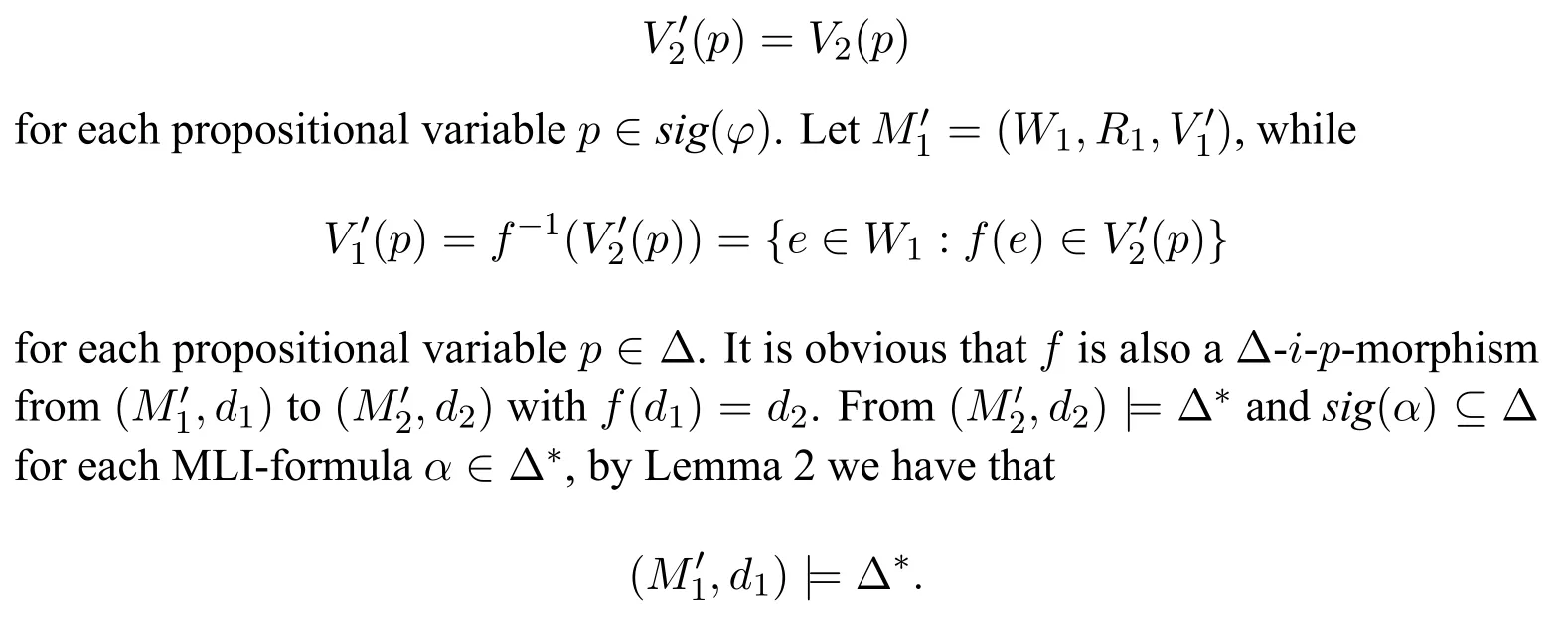
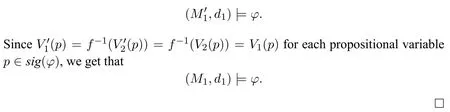
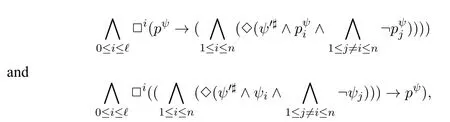

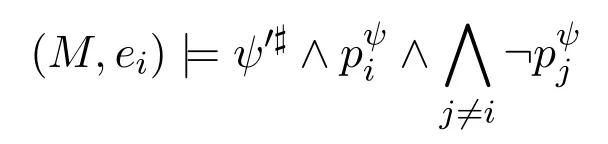
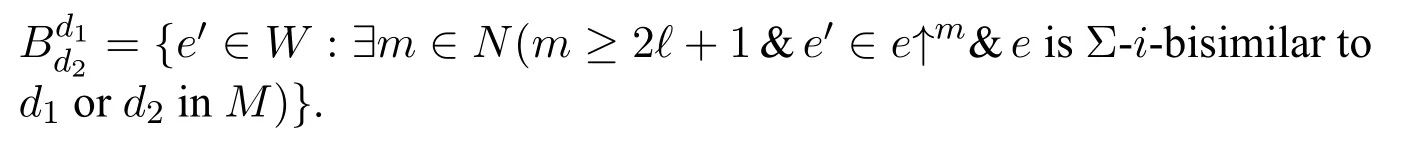
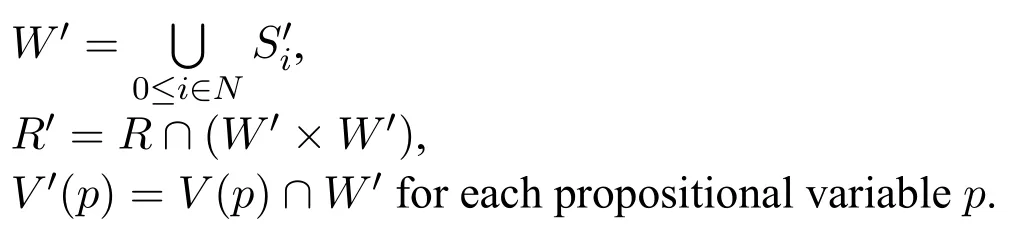
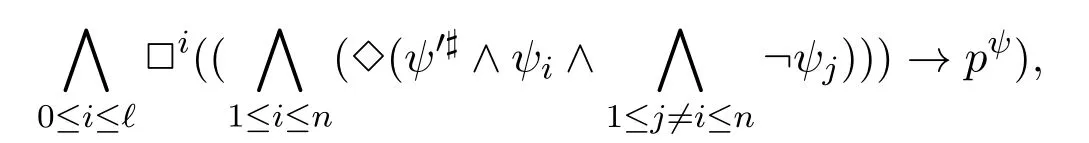
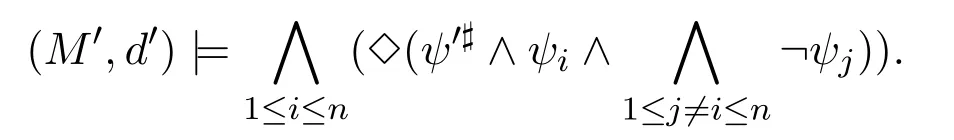
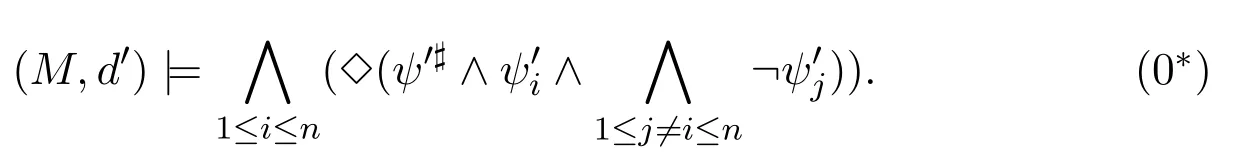


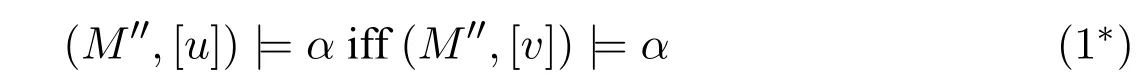
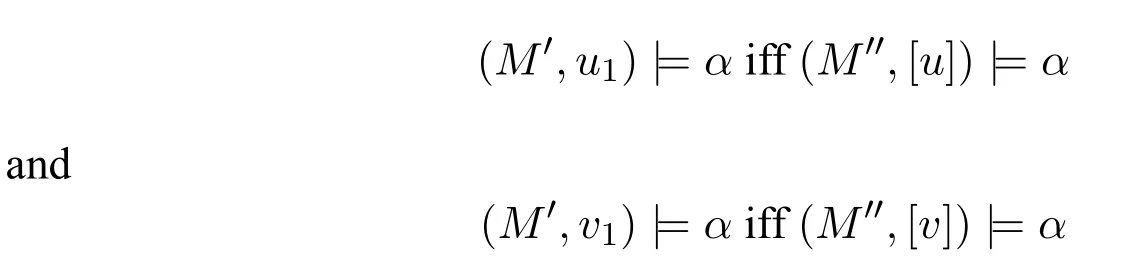
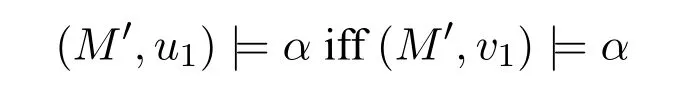
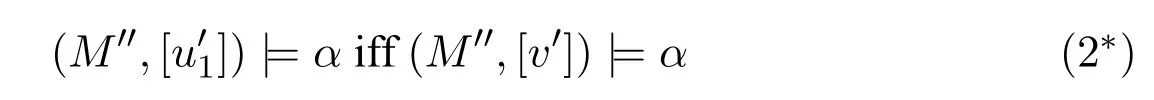
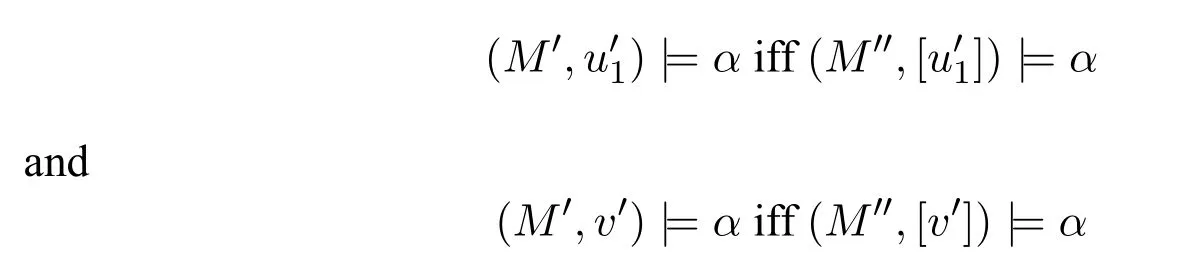
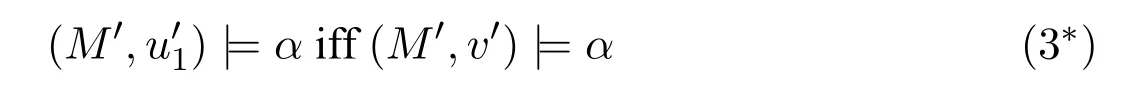
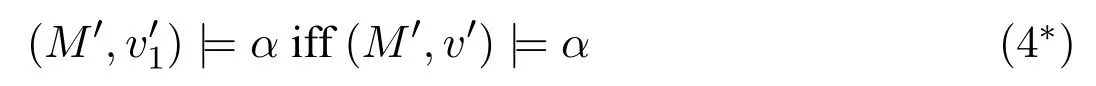
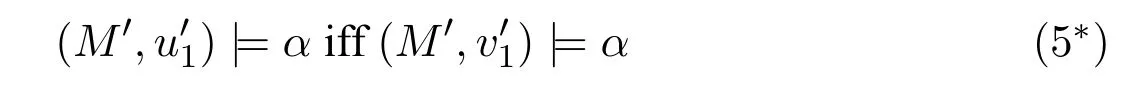
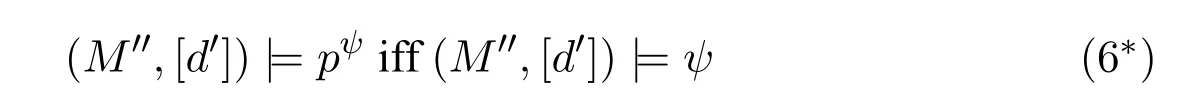
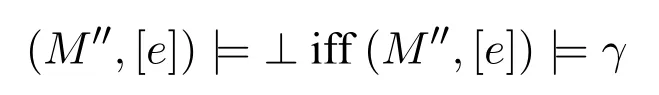

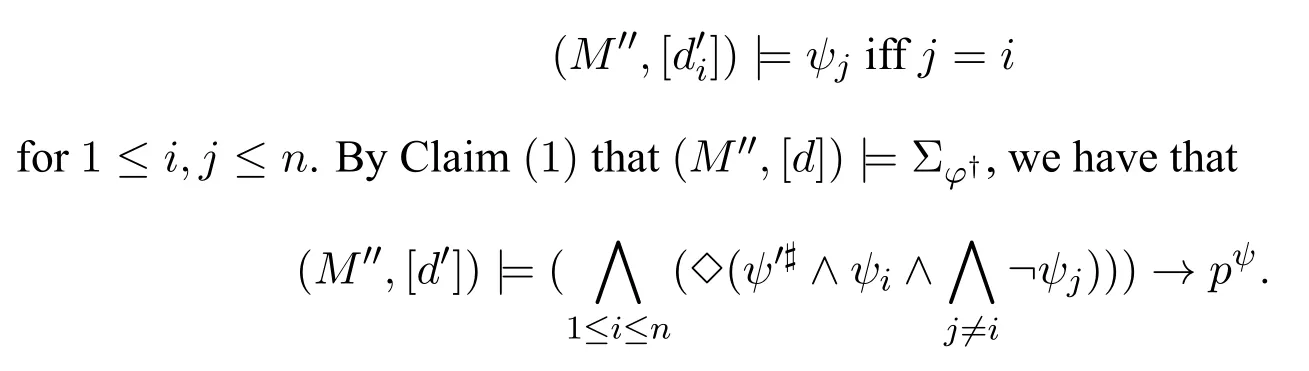


6 MLGI to ML

