A Logic that Captures βP on Ordered Structures*
Kexu Wang Xishun Zhao
Abstract.We extend the inflationary fixed-point logic,IFP,with a new kind of second-order quantifiers which have(poly-)logarithmic bounds.We prove that on ordered structures the new logic IFP captures the limited nondeterminism class βP.In order to study its expressive power,we also design a new version of Ehrenfeucht-Fra?ssé game for this logic and show that our capturing result will not hold in the general case,i.e.,on all the finite structures.
1 Introduction
In descriptive complexity theory,it is the most interesting task to find a logical characterization of a complexity class.But why do we need logics to characterize(or capture)complexity classes?
Logics speak directly about graphs and structures,whereas most other formalisms operate on encodings of structures by strings or terms.Hence a logical characterization of a complexity class is representation-independent.
—Martin Grohe([8])
We know in graph theory or database theory,more essentially we care aboutgraph properties(orBoolean queries),i.e.,the properties which do not depend on encoding.A graph property is always closed under isomorphism.This coincides with that the model class of a logic sentence is closed under isomorphism.Descriptive complexity theory intends to consider every logic sentence as a machine and vice versa.Thus every model of a sentence could be associated with an input of a corresponding machine and the logic(actually a class of sentences)would be related to a complexity class (actually a class of Turing machines).The precise definition will be given in 2.2.
In this paper,let’s turn to somelimited(orbounded)nondeterminismclasses,which are included in NP while including P.The idea of limited nondeterminism was first defined by Kintala et al.in[13].Then in[3]Cai et al.discussed a more general case,i.e.,the“Guess-then-Check”model.
Definition 1.1([3])

We care more about the second-order quantifiers with a logarithmic bound,written as.We call theselog-quantifiers.The new logicIFP is obtained by extending theinflationary fixed-point logicIFP with all the log-quantifiers.The main theorem will show thatIFP capturesβP on ordered structures.Anordered structureis a structure whose domain has a built-in linear order.One can notice that the log-quantifiers will act as the part“?v ∈{0,1}?,|v| ≤c·s(|u|)”in definition 1.1.The log-quantifiers“guess”and then the IFP formula will“check”.
Our characterization is a natural extension of the famousFagin’s theoremandImmerman-Vardi’s theorem.R.Fagin([5])showed that NP is captured by the existential second-order logic,which consists of formulas in the form
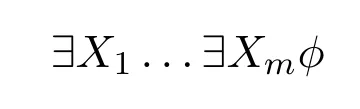
where?is first order andX1...Xmare relation variables.As a corollary of Fagin’s theorem,every layer of the polynomial time hierarchy,PH,is captured by a layer of the second-order logic.([4])The fundamental result of capturing P is Immerman-Vardi’s theorem.([11,16])It shows that IFP captures P on ordered structures.
The restriction on ordered structures is vital.Actually so far we do not know what logic can capture P without a built-in order.Logics are free from encoding,but when we intend to simulate a Turing machine with a logic sentence,it cannot be helped using a linear order to encode graphs or structures.This is related to a more fundamental and sophisticated problem,canonization(orcanonical labeling)of graphs(or structures).A canonization is an algorithm which returns the unique labeling of a graph no matter how we label the vertices of the graph initially.The P-computable canonizations do exist on some certain classes of graphs,for instance,trees([14]),planar graphs([14]),graphs of bounded treewidth([2]),graphs of bounded degree([1]).Researchers are also interested in using logics to define a canonization.There are IFP-definable canonizations on cycles([4]),grids([4])or 3-connected planar graphs([6]).That means on these classes IFP can provide a canonical linear order and captures P.An important approach is to extend IFP to capture P on some more general classes.For example,IFP with counting,denoted by IFP+#,on trees ([12]),planar graphs([6]),graphs of bounded treewidth([9]),graphs of bounded rank width([10]).
Neither IFP nor IFP+# can capture P in the most general case,i.e.,on all the finite structures.They were originally proved via the game method.Alongside this notion we will design a new Ehrenfeucht-Fra?ssé game and proveIFP fails to captureβP in the most general case,too.
2 Preliminaries
We assume that the readers are familiar with the basic concepts of computational complexity theory and mathematical logic.Asignature τis a finite class of relation symbols.For convenience we do not talk about constant symbols and function symbols.L[τ]is the formulas of logicLformed with symbols inτ.Aτ-structure(or structure overτ)Bexplains the symbols inτon a domainB.In this paper we only considerfinitestructures,i.e.,whose domain is a finite set.STRUC[τ]is the class of allτ-structures.Agraphis a structure over signature{E}whose domainVis a set of vertices.STRUC[τ] where “#”is used to separate two concatenated strings,for instance,“u#v”.are used for encoding in definition 2.1.None of the three auxiliary symbols are theoretically necessary and all strings can be represented binarily,i.e.,just with 0 and 1.However their attendance makes our proofs much easier. A Boolean queryQonτis a class of structures over the same signatureτ,and closed under isomorphism,i.e.,for anyA,B ∈STRUC[τ],if,then, For example,languages(classes of strings)are Boolean queries onτstr. In the following context,we often use the logarithmic function log(n),whose value is expected to be an integer,so we let log(n)=.Let[n]={0,1,...,n ?1}.Note that log(n+1)is the minimal length ofn’s binary expression.In this paper,for any formula?(x,X),means the valuea(resp.R)is substituted intox(resp.X)ifx(resp.X)is free.We abuse the notation|·|.Ifuis a string,|u|is its length.IfAis a set,|A|is its cardinal.Ifis ak-tuple,then=k. In order to represent the structures in a Turing machine,we need to encode structures as strings.W.l.o.g.,we take the following way of encoding: Definition 2.1(Enumerating encoding) For any signatureτ={R1,...,Rm},wherearity(Ri)=ri(1≤i ≤m),anyA ∈STRUC[τ] The length|enc(A)|is related to every cardinal.The machine needs the auxiliary symbols to parseenc(A)because it cannot know ahead of time how longis.The extra length of auxiliary symbols can be ignored in a big-Oh notation. Definition 2.2([7]) A logicL capturesa complexity classCon a classKof structures,if the following conditions are satisfied, 1.L[τ]is decidable,for any signatureτ. 2.There is an effective procedure to associate with eachL-sentence?aC-bounded Turing machine M,such that,for anyA ∈K,M can decide whether 3.For any Boolean queryQinC,there is anL-sentence?such that for anyA ∈K, (We assume thatKis closed under isomorphism.) IfKis the class of all structures,we simply sayLcapturesC. There are two most classical theorems in descriptive complexity theory. Theorem 2.3(Fagin’s Theorem,[5])captures NP. Theorem 2.4(Immerman-Vardi Theorem,[11,16]) IFP captures P on ordered structures. IFP is gotten by extending the first-order logic FO with the inflationary fixed-point operator.IFP inherits the formation rules of FO besides ? Ifψis a formula,then so iswhereYis a relation variable and=arity(Y) In logic we needn’t even study structures over all different signatures.We particularly care about STRING and graphs,which the structures over other signatures can be interpreted to. Definition 2.5LetLbe a logic.Letτ,σbe two signatures.σ={R1,R2,...,Rm},wherearity(Ri)=ri(1≤i ≤m).Ank-ary L-interpretationfromτtoσis a sieres ofL[τ]-formulas Lemma 2.6For any signatureτ,there is an FO-reductionIfrom STRUC[τ] Lemma 2.7Let?be a formula of IFP[σ], is ank-ary reduction from STRUC[τ]to STRUC[σ].?Iis obtained by ? replacing every variablexoccuring in?by a newk-tuple(which consists of all new variables,let’s denote it byxI), ? replacing every relationRiin?by, ? changing the subformula?x...in?to?xI(?uni(xI)→...), ? changing the subformula?x...in?to?xI(?uni(xI)∧...), whereY Iis anl·k-ary new relation variable. Then forA ∈STRUC[τ], These two lemmas tell us STRING and ordered structures are deeply related.LcapturesCon STRING if and only ifLcapturesCon ordered structures.In the following context,we will first prove our theorem on STRING,and naturally it holds on ordered structures. Here is an alternative definition ofβP prepared for our later proofs: Definition 3.1A languageLis in the classβkif there is a languageL′ ∈P together with an integerc >0 such that for any stringu,u ∈ Lif and only if?v ∈,u#v ∈L′.(whereis all the 0-1 strings of length at mostc·logk(|u|).) Sinceβ1=GC(log,P),in fact the“guess”part can be computed in time 2c·log,which is a polynomial.Thus we have It doesn’t matter how largearity(X) is.As long asarity(X) is a nonzero natural number,can be applied.Naturally Definition 3.2An formula ofIFP is in the form, wherem ≥0;k1,k2,...km >0;ψis an IFP-formula. Those formulas without any occurrences of log-quantifiers arelog-quantifierfree. Here are three parameters we will use.Themaximal variable arityof a formula,mva(?)=max{arity(X)| Xis a relation variable,free or bounded by a log-quantifier,in?}.Theheightof a formula,height(?)=max{k |occurs in?}.Thelog-quantifier rankof a formula, ?lqr(?)=0,if?is atomic ?lqr(?)=lqr(ψ),if?=?ψ ?lqr(?)=max(lqr(ψ1),lqr(ψ2)),if?=ψ1→ψ2 ?lqr(?)=lqr(ψ),if?=?xψ ?lqr(?)=lqr(ψ)+1,if?=Xψfork >0. Fork >0,IFP is the sublogic ofIFP,the heights of whose formulas are no larger thank. Theorem 3.3IFP capturesβP on STRING. Proof IdeaActually we will prove fork ≥1,IFP capturesβk+1on STRING.Note that anIFP[τstr]-sentence corresponds to aβk+1-bounded Turing machine,not aβk-bounded one.It is because for anyu ∈STRING and any relation varibleX,when we encode the value ofX,as we did in definition 2.1,|enc(X)|=|O(logk+1|U|)|.According to definition 2.2,our proof consists of three parts.The main idea is simple:we use“X”to simulate“?v ∈”in definition 3.1 and vice versa;then we apply Immerman-Vardi’s theorem. But here is a problem:for anyvin “?v ∈” in definition 3.1,can we have an IFP-reductionIsuch that there existsXin“X”andI(X)=v? Lemma 3.4Letk ∈N?{0} There is an encodingJsuch that for any stringuwith domainU,JUis asurjectionfrom{S |S ?U2and|S|≤logk(|U|)}to. And letτr=τstr∪{R1,R2,...Rr},whereR1,...Rrare binary relation symbols.There is an IFP-reductionIfrom STRUC[τr]to STRING such that for anyu ∈STRING and binary relations∈{S |S ?U2and|S|≤logk(|U|)}, Proof(of lemma 3.4) For anyS ∈{S | S ?U2and|S| ≤logk(|U|)},JU(S)is gotten by doing as follows 1.gettingenc(S); 2.removing the first element of each tuple ofSfromenc(S); 3.removing the log(|U|)-th bit of each consecutive binary substrings in the encoding; SoJU(S)=110000 in this example. It is easy to verify thatJUis a surjection. Now we construct the IFP-reductionI.With the help of the linear order Let=x1x2x3x4x5yz1...zlog(r).It’s an(log(r)+6)-ary tuple of variables.Now we define: Proof (of theorem 3.3) By definition 2.2,our proof consists of three parts.Letk >0. In the above proof,we can see only binary relation symbolsR1,...Rrare bounded by the log-quantifiers.So we obtain Corollary 3.5On ordered structures,every formula ofIFP is equivalent to a formula ofIFP whose bounded relation variables are binary. IFP fails on a very important P-decidable Boolean query,EVEN.([4])For any graphG,G ∈EVEN if and only if domain|V|is even.There isnosentence?of IFP[{E}]such that (EVEN is not definable in IFP.) So IFP fails to capture P (on all finite structures).Unfortunately,our strengthened versionIFP fails,too. Theorem 4.1EVEN is not definable inIFP. IFP’s failure was proven via the failure of the infinitary logic.The logicis similar to FO,but every formula incan have infinite length or infinite quantifier depth and contains at mostsvariables(free or bounded).Then For the details readers can turn to [4,ch.3].For every single IFP-formula,we can always construct an equivalentfor somes.So IFP is a sublogic of.Now we define a new logicL(Beware! It is notL!) as follows:for any formula? In order to prove theorem 4.1,we turn to the game method Definition 4.2Lis any logic.G is a game played by two players,the spoiler and the duplicator,on two structures.we say G is an Ehrenfeucht-Fra?ssé game forL,if for anyτ,anyAandB ∈STRUCT[τ],the following are equivalent, 1.A ≡L B 2.the duplicator wins G(A,B) where“A ≡L B”means for anyL[τ]-sentence?,A??if and only ifB??. The Ehrenfeucht-Fra?ssé game foris the pebble game withspairs of pebbles,denoted by PGs.In a play of PGs(A,B),there ares(or less)vertices in each ofAandBcovered by pebbles.In each move,each player can do nothing,move one pebble or add a new pebble(but on each structures there can be at mostspebbles).If the duplicator can make sure the two covered substructures are always isomorphic,then she wins PGs(A,B).For the details readers can turn to[4,ch.3]. Now letLm,r,k,sbe the sublogic ofLsuch that for any?in it, ?lqr(?)≤m, ?mva(?)≤r, ?height(?)≤k, ? at mostselement variables occur in?. Proposition 4.3Form ≥0,r,k,s >0,Gm,r,k,sis an Ehrenfeucht-Fra?ssé game forLm,r,k,s. ProofLetAandBbe two structures over a given signatureτ. Theorem 4.4EVEN is not definable inL. ProofIf EVEN is defined by a sentence?ofL[{E}],?should also work on empty graphs,namely on the graphs that have no edges.Now we assumeE=?in order to get a contradiction.There arem ≥0 andr,k,s>0 such that? ∈Lm,r,k,s[{E}].LetAandBbe two empty graphs such that|A|is a sufficiently large even number satisfying Readers might have noticed that the results can be extended onto other complexity classes.For example the existential and universal log-quantifiers can alternate several times in the formula so as to capture a correspondinglimited alternation class.Furthermore,not only log-quantifiers,we can also consider other second-order quantifier with a bound of cardinality.Letfbe a sublinear function on N.One can easily prove on ordered structures a logic“?fIFP”can captureβ(f·log),i.e.,the complexity classGC(f(n)·log(n),P),where the parameter“l(fā)og(n)”seems unavoidable.However none of the above can capture the corresponding complexity classes without a linear order.The proofs could be analogous to our theorem 4.4. We are not sure ? on whatnaturalclass of graphs,IFP can captureβP while IFP cannot capture P. ? whether there is a problem in P whichIFP can define while IFP cannot. These questions could be interesting.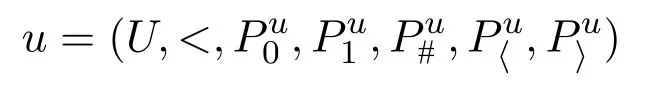
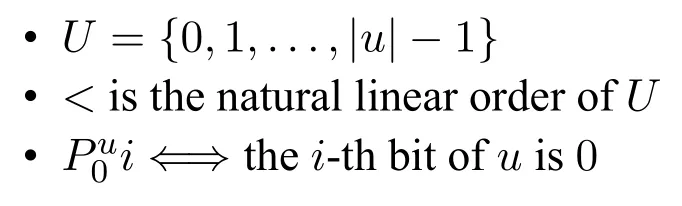


2.1 Encoding structures

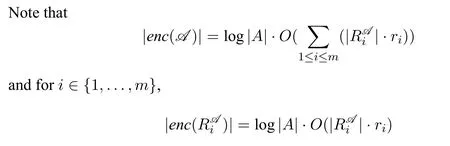
2.2 Logic characterization of complexity
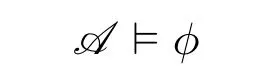
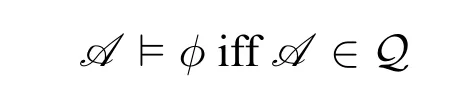

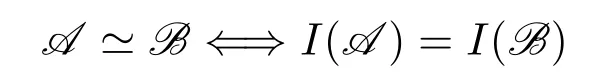
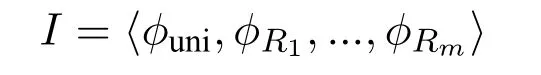
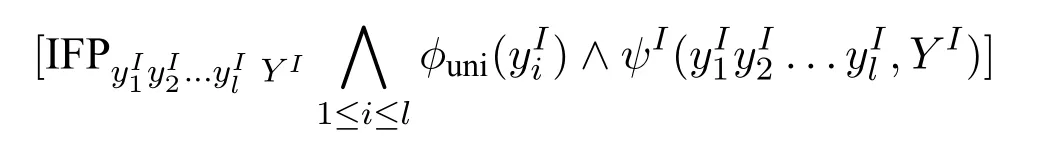
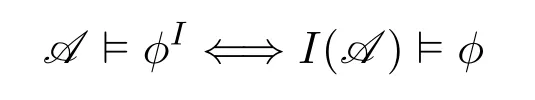
3 Capturing Results
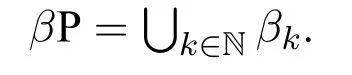
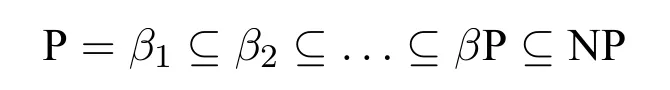
3.1 Logarithmic-bounded quantifiers
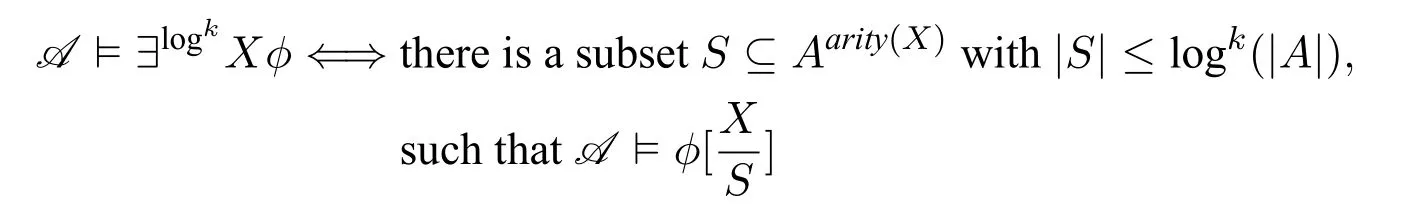
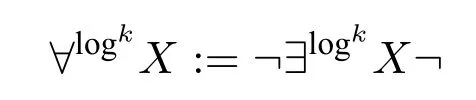
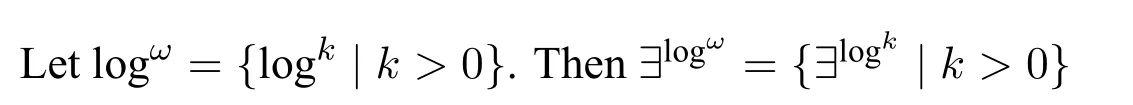
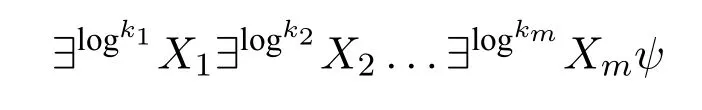
3.2 Main theorem
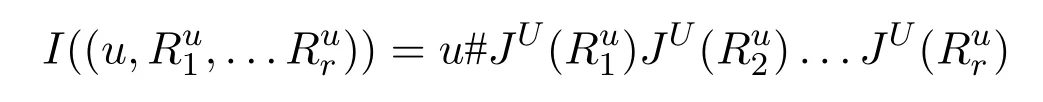




4 The Expressive Power
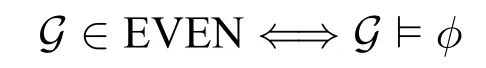
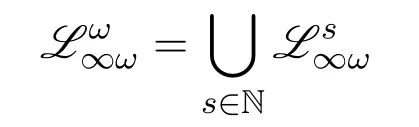


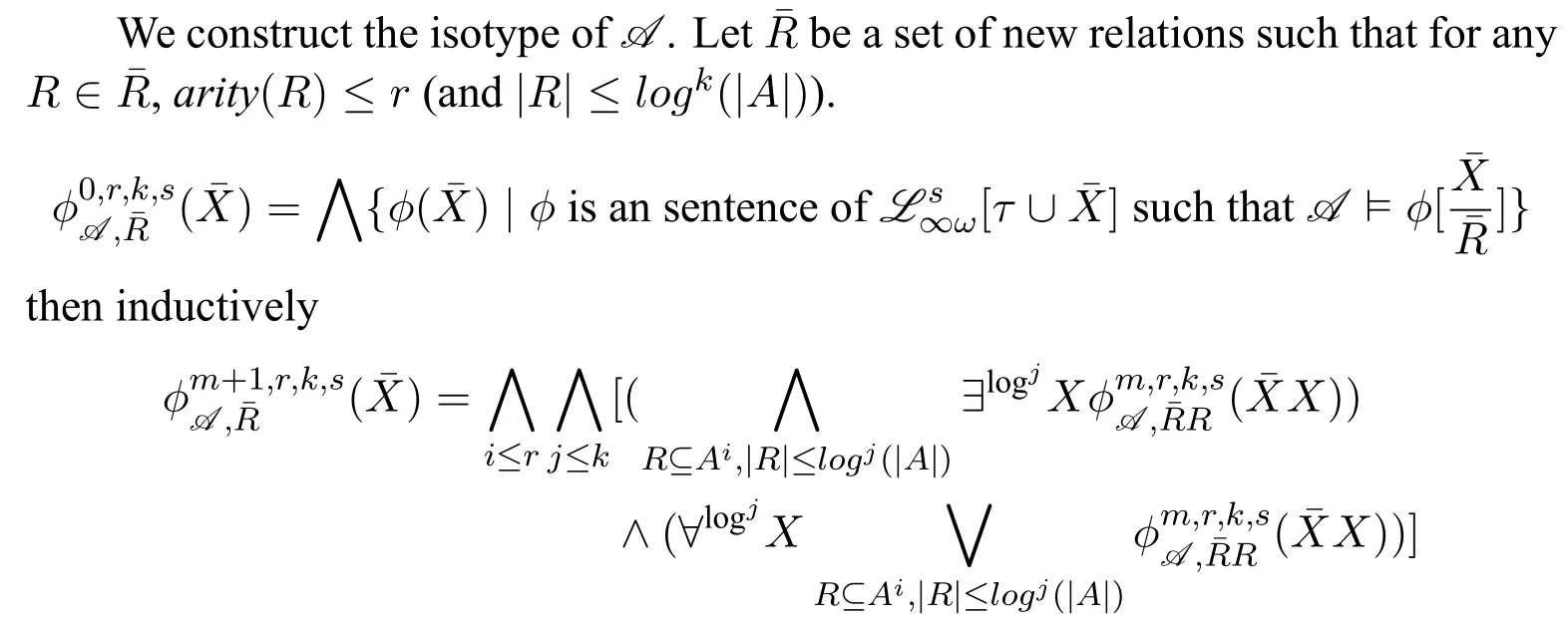


5 Furthur Discussion

