Difei Xu

Abstract.Fine (2016) provides some kinds of truth-maker semantics that explain how we understand our language,but these are controversial,especially in how we understand universal sentences.In his unpublished paper,Hale modifies Fine’s standard exact truth-maker semantics to explain how we understand law-like universal statements.In this paper,I suggest that if Hale insists that exact truth-maker semantics clauses for law-like universal statements differ from those for accidental universal statements,it would be better for Hale to formulate a lawlike generalization and an accidental generalization in different logical form,although the first entails the latter one.I also provide exact-truth-maker semantics for law-like generalization different from Hale’s.In the last part of this paper,locating universal statements in inexact truth-maker semantics,I compare the two formulations of the lawlike universal statements.

1 Truth-condition Semantics and Its Different Approaches

Frege first to formulated the meaning of a sentence according to its truth conditions.In Frege’s opinion,natural languages are so misleading that it quite difficult for us to explain how we understand them.For his philosophical aim,he set up a brand new logical language,transparent in its logical structure.One of his concerns was to explain the meaning of an artificial language that has atomic sentences which form all the complicated sentences are formed by the atomic sentences with connectives,quantifiers,and variables.Nowadays,it is well known that truth-condition semantics explains how truth conditions of complicated sentences depend on truth conditions of constituent sentences.

Truth-making semantics is a kind of truth condition semantics.

The main idea of truth-making is the idea of something on the side of the world—a fact,perhaps,or a state of affairs—verifying,or making true,something on the side of language or thought,a statement,perhaps or a proposition.As Fine([5])points out,this idea has figured prominently in contemporary metaphysics and semantics.Some philosophers,such as Armstrong,apply truth-making to arrive at a satisfactory metaphysics,asserting what on the side of the world makes statements or thoughts true.This application is a route from the language or thought side to the world side.In application of semantics,the main concern is how sentences are made true by what is in the world.This application is a route from the side of the world to the side of language.Fine’s truth-making semantics,from the very name,we know is the application of the truth-making idea to semantics.

Fine classified different approaches to truth-condition semantics.([5])Basically,truth-condition semantics has two kinds of approaches:the clausal approaches,the first such as suggested by Davidson ([4]),on which truth-conditions are not given as entities but by clauses specifying when a statement is true;and second,objectual approaches,according to which truth-conditions are not clauses but worldly entities that stand in truth making relation to statements they make true or false.In objectual approaches,we should also distinguish two kinds of approaches:one takes possible worlds as truth-makers,and the other takes states or situations as truth-makers.The main difference between a possible world and a state(or a situation)lies in that the former can decide any statement’s truth value,while the latter cannot.For example,the state of weather in Beijing cannot settle whether it is raining in Padua.Truth-maker semantics is ojectual,taking states as truth-makers.“Possible worlds semantics”received its first systematic application to natural language in the work of Montague.([7])“Situations or states semantics”received its first systematic development in the work of Barwise and Perry.([3])

Even states semantics contains further division,that is,exact truth-maker semantics,inexact truth-maker semantics,and loose truth-maker semantics.In this paper,I will focus on the first two,especially on truth-maker semantics for universal statements.But before our exploration,I provide a brief introduction to standard exact truth-maker semantics according to Fine.

2 Brief Introduction to Standard Exact Truth-maker Semantics

If we introduce constantsa1,a2,···into the language,for each of the distinct individualsa1,an,···inA,the clauses for exact truth-maker semantics for atomic and complex statements may be defined as follows:

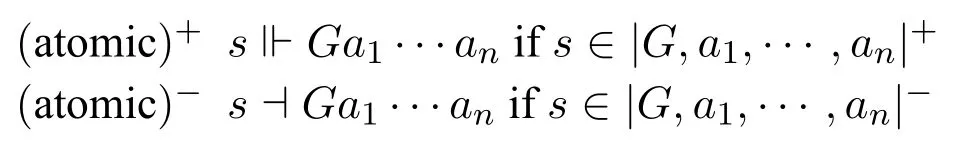
3 Some Features of Exact Truth-maker Semantics

3.1 States in semantics

The states in Fine’s standard truth-maker semantics are just terms of art that need not stand for a state in any intuitive sense of the term.

It should be noted that our approach to states is highly general and abstract.We have formed no particular conception of what they are;and nor have we assumed that there are atomic states,from which all other states can be obtained by fusion.([5],p.4)

Fine ([5]) suggests distinguishing truth-makers in metaphysics and semantics.He does not agree that the truth-making idea provides a guide to metaphysics.Fine’s truth-maker semantics,as he says,concerns how truth-makers(states of affairs)make statements in our language true.

The idea of truth-making is the idea of something on the side of the world,a fact,perhaps,or a state of affairs,verifying,or making true,something on the side of language or thought,a statement,perhaps,or a proposition.The idea of truth-making has figured prominently in contemporary metaphysics and semantics.In its application to metaphysics,the thought has been that we can arrive at a satisfactory metaphysical view by attempting to ascertain what it is,on the side of the world,that renders true what we take to be true(as in[1]and[2]);and,on the semantical side,the thought has been that we can attain a satisfactory semantics for a given language by attempting to ascertain how it is that the sentences of the language are made true by what is in the world.In the former case,truthmaking serves as a conduit taking us from language or thought to an understanding of the world;In the latter case,it has served as a conduit taking us from the world to an understanding of language.([5],p.4)

3.2 Exact truth-makers

According to Fine,the exact truth-maker of a statement should be wholly relevant to the statement.

Both exact and inexact verification require a relevant connection between state and statement.With inexact verification,the state should be at least partially relevant to the statement,and with exact verification,it should be wholly relevant.Thus,the presence of rain will exactly verify the statement‘it is rainy’;the presence of wind and rain will inexactly verify for the statement‘it is rainy’,though not an exact verifier;and the presence of wind will be a loose verifier for the statement’it is rainy or not rainy’(since the statement is true no matter whether rain is present),while failing to be an inexact verifier.

However it is wrong to think that an exact truth-maker of a statement is the minimal state that makes it true.Let us considerp ∨(p ∧q).According to exact truth-maker semantics,

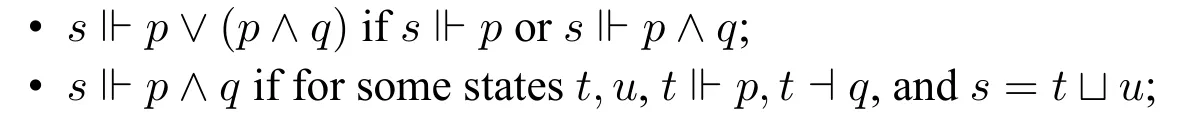
? therefore,the exact verifier ofpand the exact verifier ofp ∧qare both exact truth-makers ofp ∨(p ∧q),although the latter includes the first.

From this example,it is easy to see that a state could be an exact truth-maker for different statements1In this example,s is not only the exact verifying statement of p,but also of p ∨(p ∧q).,and a statement may have different exact truth making states.2In this example,p ∨(p ∧q)may have different states exactly verifying its truth.

4 Quantifiers

4.1 Two kinds of generalization

As for universal statements,Hale urges us to notice the difference between two kinds of generalization.To illustrate the difference,let us consider the two statements in the following:

Example 1

? All cats are born blind.

? All the students in my logic class are male.

The first statement is law-like,and we might think that there are no contractual instances for this universal statement;the second statement is accidental,and we might think of contractual instances of the universal statement.We represent these thoughts as the following statements:

Example 2

? If the cat were justly born,he would have been blind.

? If Alice were in my logic class,she would have been male.

These two examples may show the difference between the two kinds of generalization.However the standard exact truth-maker semantics for them are same.Hale thinks that an adequate semantics for generalization should tell the difference between the two kinds.But Fine’s standard truth-maker-semantics cannot account for the difference,and therefore we should fix that.

4.2 Hale’s Way

Hale does not suggest that the two universal statements in example 1 are in different logical forms,but he insists that although they are in the same logical form,the clauses for exact truth-makers in semantics for the two kinds of general statements should differ.The law-like and accidental universal statements have the same logical form:?x(Hx →Gx).For the exact truth-maker semantics of accidental universal statements,Hale,suggests we should extend the valuation|:|to assign to the paira pair,the former comprising states which verifyGof anyntuplea1,a2,···analso verifyFand the second comprising those states which falsifyGof anyn-tuplea1,a2,···anbut verifyF.We may denote the set of states of the first kind by,and the second by.

Hale’s modification of exact truth-maker semantics is a kind of restriction of the model.Firstly,we collect all individuals forsverifyingFofa.Secondly,forsif it is also the verification ofGfor all the collected individuals,thens ∈.Fors,ifsis a falsification ofGfor some collected individual,thens ∈.Exact truth-maker semantics for accidental universal statements essentially differ from law-like ones.From the above,we see that this semantics for accidental ones does not resort to the meaning of material implication.To contrast with the law-like ones,it is better to formulate the accidental ones in the form?x(Hx ?Gx)

For the law-like universal statements,Hale asks for different requirements.To simplify the explanation,it is better to introduce the connective→.Like classical semantics for material implication,Hale introducesH →Gas the abbreviation for?H ∨G.

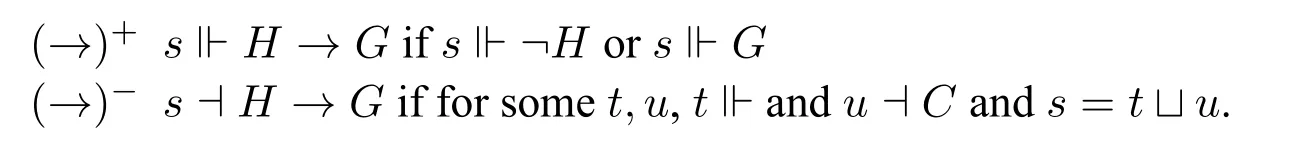
To make the explanation more easier,letFandGbe monadic predicate.

Hale suggests that ifsis a verifier of the law-like universal statement?x(Hx →Gx),thensshould be the verifier for the open statementHx →Gx,no matter which individualain the domain is taken as the value ofx.If a state verifies or falsifies the open statement,then the state is a generic state.

It is easy to prove that ifsis a general state verifying or falsifying a law-like universal statement,it is also a verifying or falsifying the universal statement as accidental statement.

5 My Modifications for Quantifiers

I agree with Hale that semantics should be adequate to account for the semantic difference between law-like and accidental universal-statements.I am also in sympathy with Hale’s proposal against taking the law-like generalization in necessary form.Drewery proposes that the law-like universal statement should have a logical form different from the accidental one’s,and her suggestion for the law-like involves necessity,and might be represented as the logical form □?x((Hx ∧Gx)?Gx).Here I do not wish to explain in detail why this kind of suggestion involving necessity like Drewery’s is not attractive.But the main reason I do not take this suggestion is that here,we wish to provide the exact verifier or falsifier of law-like universal statements,and the truth-maker for necessity is loose but not exact.Unless there are no exact truth-makers for universal statements,we do need to consider the exact truthmakers for the universal statements.There is no sufficient reason to deny the exact truth-makers of universal statements.

No matter what logical form represents a law-like universal statement,it entails?x(Hx →Gx).The main concern is how to explain semantic conditions for universal statements and more special requirements for law-like ones.I do not mean that the two statements in example 1 are in the same logical form,instead,I suggest,since their semantic requirements differ,they are take different logical forms.Hale suggests the two are in the same logical form,but at the same time gives different semantic clauses for the two kinds of universal statements.It might not be a big deal since we wish to explain the two kinds of universal statements,and even if we use the same symbols representing the two kinds of statements,the semantic clauses differ.Of course,once we explain the form in two different ways,the one form essentially represents two different forms.

Naturally,as for an accidental universal-statement,like“All the students in my logic class are male,”if we say thatsis the exact verifier of this statement,we expect thatsincludes statetverifying“a1is in my logic class;··· anis in my logic class”,includes some other states respectively verifying“a1is in my logic class,···,anis in my logic class”.The fusion of all the states iss.The fusion of the states is an upper-bound of these states,respective to the partial order?in semantics.It should also be noticed that the exact verifier is not hereditary in the sense that ifsis an exact verifier for a statement,andtincludess,then generallytis not an exact verifier of the statement.

In Hale’s modification,an exact verifiersfor a universal statement should be the exact verifier of all the instances.But there is no good reason whysshould be the exact verifier for the instances but not inexact instead.For an accidental statement,like “Tom is in my logic class,” “John is in my logic class.” Exact verifiers for the two statements are not supposed to have an internal relationship,and the fusion of the two verifiers is the conjunction of the two statements.However in Hale’s modification,if a state is an exact of some universal statement,no matter whether it is law-like or accidental,this state at least includes exact verifiers for the instances.Fatherly,the verifier for an accidental universal-statement should also include a statetcollecting all individuals thatFholds of.To decide whether it is true that all students in my logic class are male,I should see which are in my class and whether they are male.Therefore,tcollecting all individuals thatFholds,should be part of the verifier.Hale suggests extending the valuation is just to consider the state collecting all the individuals thatFholds.Therefore,I almost agree with his modification;the minor difference is that I require only that the verifier include verifiers for instances.Briefly,I suggest adopting Fine’s exact truth-maker semantics for?,and explain accidental“AllAs areBs”just by restriction to domain.I formulate this logical form as?x(A(x)B(x)).

I also agree with Hale that the law-like universal statements might not concern the domain of a model.“All cats are born blind,” no matter whether the cats are deceased,alive,or born in the future.As for this statement,we might not even collect all individuals being cat.Hale proposes that ifsis a verifier for the law-like universal in the form?x(Hx →Gx) should be a generic statement that is a verifier for the open statement in the formHx →Gx.My worry is the semantics for the connective of material implication.

The exact verifier“All cats are born blind”should also verify“Tom is not a cat,and he is not born blind”or“Cooky is a monkey,and he is unluckily born blind”,and etc.In Hale’s modification for the law-like,verifiers also take all individuals in the domain into account.Furthermore,the generic state is not only the verifier for this universal statement but also an exact verifier for“any individuals being cat are then being born blind.”

In my opinion,the law-like universal statement “allFs areGs” is about the relation between two concepts rather than individuals.I think Hale also agrees with that.He says:

For as I there suggested,even in cases where the domain of quantification is finite,but open ended,as with many ordinary non-accidental true generalizations,there is reason to doubt the availability of an instancebased explanation of their truth.If one accepts that such generalizations are true(and not merely that they will eventually—when the world ends—be true),and one further accepts that the states which make their instances true exist only if,and when,the objects involved in them exist,and that instances concerning as yet non-existent objects,even if stateable,cannot be made true by states which do not (yet) exist,then there is reason to doubt that those generalizations can be made true by states which are the fusions of states verifying each of their individual instances.([6])

The point is that,Hale’s resolution does not realize his wish.As I said before,in Hale’s modified semantics,the verifier of a law-like universal statement should take into account all individuals in the domain,and they cannot be beyond the domain.But I do not think it is promising to realize the wish in model theoretic semantics,as in the true-maker semantics.The main reason is that the universal quantifier is explained by the notion of domain.Unless we reject this idea,there is no hope to realize our wish.

Hale interprets the connective inH →Gas the abbreviation for?H ∨G.I would rather interpret it like this:The exact verifier ofFincludes the exact verifier ofG.Inspired by[5](in part II Application,§1),I first formulate semantic clauses forH ?G,and then introduceH →Gby abbreviation forH ∧G ?H.

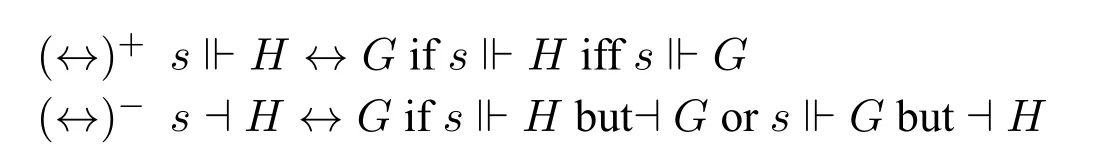
We define a verifier or falsifier of a statement by induction on its structure,and intuitively,truth-makers have some structure that also decides whether a state is a truth-maker of a given statement.For example,the verifiersofA ∧Bshould also witness the structure of states,for it requires thatsinclude an exact verifier ofB.Generally speaking,truth-maker semantics of complicated statements concerns the structure of states.

Intuitively,sis a verifier ofA ?Bif (sis a verifier ofAif and only ifsis a verifier ofB).Notice:These clauses for verifiers or falsifiers are defined by induction,and they are nested.As for?A,its verifier is just a falsifier ofA.Therefore the induction is two lateral,in contrast with the usual semantics,which is unilateral.Generally,Gdoes not mean ??Gor?G.

As for law-like universal statements in the form ofA →B,clauses could be formulated as in the following:

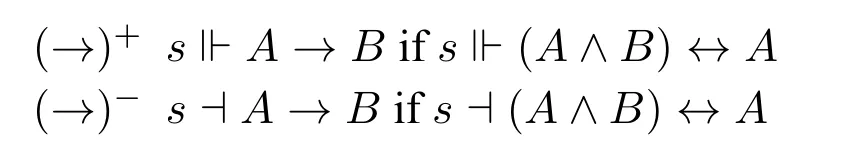
We could infer semantic clauses for law-like universal statements in the form?x(Hx →Gx)as in the following:

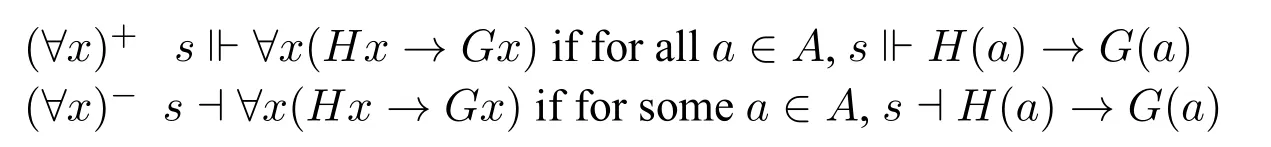
Although prima facie,here,semantic clauses for law-like universal statements are the same as Hale’s,they differ because the semantic clauses for→are different.

6 Comparison Between Hale’s and My Semantics for Law-like Universal Statements

6.1 The difference

To explain the difference between Hale’s and my semantic for law-like universal statements,let us consider the verifiersof?x(Fx →Gx)in Hale’s semantics:

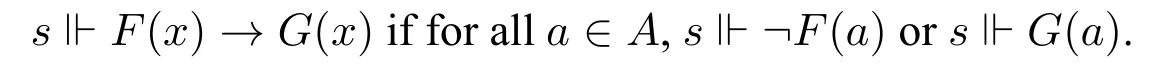
Now lets?F(a),if?x(Fx →Gx); then,because of the exclusiveness of semantics(scannot be both verifier and falsifier of any statement),s ?G(a).

However,in my semantics,this is not necessarily so.Again lets?F(a),if?x(Fx →Gx);then,s?F(a)∧G(a).Therefore,sshould include an exact verifiert,t?G(a).From this,we seesshould not necessarily be the exact verifier ofB.

This example sufficiently shows that Hale’s and my semantics differ.

6.2 The strength of the four logical forms

To make the explanation easier,in my modification,the law-like universal statement’s logical form is?x().

It is natural to ask the strength order of the four logical forms:s??x(Hx →Gx),s??x(),s??x(Hx ?Gx),s?Hx?Gx).

Claim 1s??x()ands??x(Hx →Gx)cannot infer each other.

ProofLets??x(Hx →Gx).From the requirement in Hale’s semantics,s ?H(a)ors?G(a)for alla ∈A.Ifs ?H(a),thens?G(a).So,for alla ∈A,ifs?H(a),thens?H(a)∧G(a).This does not means??x(Hx →Gx)can infers??x(),we need another direction.For anya ∈A,ifs?H(a)∧G(a),ands??x(Hx →Gx),then for somet,u,t?H(a),u ?G(a),ands=u ?t.But we cannot infers?H(a).Therefore,we cannot infers??x().

Now lets??x().For anya ∈A,ifs?H(a),thens?H(a)∧G(a).Neither could we infers?G(a).Therefore we cannot infers??x(Hx →Gx)froms??x().

From the above,we cannot compare the strength betweens??x()ands??x(Fx →Gx). □

Claim 2s??x()entailss??x(Hx ?Gx).

ProofNow lets??x().For anya ∈A,ifs?F(a),thens?F(a)∧G(a).sisalsothe exact verifier of instances ofF(a); thensshould exactly verify these instances beingG.Therefore,s??x()entails the corresponding accidental universal-statements??x(Hx ?Gx). □

Claim 3

(i)s??x(Hx →Gx)entailss??x(Hx ?Gx).

(ii)s??x(Fx ?Hx)entailss??x(Fx?Hx).

Proofs for the two claims are very easy.

7 Inexact Truth-makers

7.1 Hereditariness

Exact truth-makers are not hereditary in the sense that ift?A,andt ?s,thensmay not be an exact verifier ofA.Exact truth-makers?A ∧Bdoes not entails?A,ors?B.The following example may illustrate the feature well:

t1?Aandt2??A,t1?t2=s.Butsis not exact verifier or falsifier ofA.Althoughs?A ∧?A,this does not entail inconsistency in the semantic theory of truth-makers.sis a fusion oft1andt2,althought1andt2are incompatible.The basic rule for semantics is that a statement cannot be both an exact verifier and a falsifier of a statement.This example does not break the rule,forsis just an exact verifier ofA ∧?A,but not an exact verifier both ofAand of?A.

Unlike exact truth-makers,the inexact truth-maker is hereditary.Before I explain the hereditariness of inexact truth-maker semantics,Fine’s inexact truth-maker semantics should first be introduced.

Generally,an exact truth-makersof statementAis also an inexact truth-maker ofA.The exact truth-maker should be relevant as a whole to the statement that it makes true,but the inexact truth-maker should be relevant either in part or as a whole to the statement that it makes true.

∧:A state is an inexact truth-maker for the conjunctionA ∧Biff it is an inexact truth-maker for each conjunctBandC.

∨:A state is a falsifier for the disjunctA ∨Biff it is a falsifier forAandB.

?x:A state is a truth-maker for the universal quantification?xA(x)iff it is a truthmaker for eachA(a1),A(a2),···.

?x:A state is a falsifier for?xA(x) iff it is a falsifier for each-maker for eachA(a1),A(a2),···.

Clauses for negation,negative clauses for conjunction and universal quantification and positive clauses for disjunction and existential quantification are the same as exact semantics.

Let us state some basic rules for inexact semantics:

(i) (Exclusiveness)The state cannot be both a verifier and a falsifier of a statement.

(ii) (Hereditariness)If statementtis a truth-maker of statementA,andtis a part of states,thensis a truth-maker ofA.

7.2 Some basic features of connectives in inexact truth-maker semantics

From the inductive definition of the inexact truth-maker for the statements,there are some basic results in this semantics:

(i) There is nos,such thats?A ∧?A.

(ii) There is nos,such thats??(A ∨?A).

(iii) Ifsis an exact truth-maker of statementA,thensis an inexact truth-maker ofA.

7.3 Reconsider the law-like universal in inexact truth-maker semantics

In this semantics,let us reconsider the law-like universal statement in inexact truth-maker semantics.Following Hale’s proposal,

s??x(Fx →Gx)if for alla ∈A,s??Faors??Ga.

Claim 4s??x(Fx →Gx)entailss??x().

ProofSupposes??x(Fx →Gx).For anya ∈A,ifs?Fa,thensis not a verifier of?Fa.By Hale’s definition,s?Ga,sos?Fa ∧Ga.

Supposes??x(Fx →Gx).For anya ∈A,ifs?Fa ∧Ga,thens?A.

Therefores??x(). □

Supposes??x().For anya ∈A,sis a verifier ofFaiffsis a verifier ofFa∧Ga.Then,for anya ∈A,ifsis not a verifier of?F(a),thensis not necessarily a verifier ofF(a).At the same time,sis not necessarily a verifier ofGa.

Example 3Ais the domain of a model,andsis a state of this model.Butsis not a verifier ofF(a8),G(a8) nor a falsifierF(a8).But for anya ∈A,sis a verifier ofFaiffsis a verifier ofFa ∧Ga,sos??x().At the same timesis not a verifier of?F(a8)and not a verifier ofG(a8).Thereforesis not a verifier of?x(Fx →Gx).

This example shows that in inexact semantics,s??x() does not entails??x(Hx →Gx).

Definition 4(Exhaustiveness) If the valuation|:|of a model satisfies the condition:for any statementA,for any state in the model,sis verifier or falsifier ofA,then the valuation or the model is exhaustive.

Claim 5M is a model,andsis a state in the model.If M is exhaustive,then in the inexact semanticss??x()entailss??x(Hx →Gx).

ProofSupposes??x().For anya ∈A,sis a verifier ofHaiffsis a verifier ofHa ∧Ga.Then,for anya ∈A,ifsis not a verifier ofH(a),then by exhaustiveness,it is a falsifier ofH(a),that is,s??A,sos?H(a)→G(a).Ifsis a verifier ofH(a),then by definition ofs??x(),s?H(a)∧G(a).By the definition of∧,s?G(a),sos?H(a)→G(a).Therefores??x(Hx →Gx).□