基于擴(kuò)張狀態(tài)觀測器的車輛橫擺穩(wěn)定模型預(yù)測控制器設(shè)計(jì)
曲 逸 許 芳 于樹友 陳 虹李宗俐
(1.吉林大學(xué)汽車與仿真國家重點(diǎn)實(shí)驗(yàn)室,吉林長春 130025;2.吉林大學(xué)通信工程學(xué)院,吉林長春 130025;3.同濟(jì)大學(xué)新能源汽車工程中心,上海 201804;4.中國一汽集團(tuán)公司研究設(shè)計(jì)中心,山東青島 266000)
1 Introduction
In recent years,vehicle stability control has received significant attention and become a major research area.Under poor driving conditions,such as extremely wet and snowy roads,most drivers may show panic reactions and become unable to coordinate steering,braking and throttle commands in a timely and effective manner,so that the actual running state of the vehicle and the driver’s intention are greatly deviated.The deviations may result in vehicle offset and instability,which put passengers at risk.Therefore,it is necessary to design a vehicle stability control system to intervene the vehicle timely and correct its state before the danger occurs[1].
Nowadays,various methods have been studied for vehicle yaw stability control.The classical control method is PID controller for vehicle safety and stability[2].However,PID is still not suitable for some complicated and extreme maneuvers in vehicle systems.Hence,many modern control methods have been introduced such as fuzzy logic control,triple-step nonlinear method,sliding mode control and robust control.Fuzzy logic control[3]and triple-step nonlinear method[4]can simplify the nonlinear complexity of vehicle system design.However,the fuzzy rules of the control strategy and the map using in triple-step method are mostly decided by experience,which would be easily ineffective with unexpected maneuvers.Sliding mode control[5]can achieve fast dynamic response,but the undesirable chattering always exists in the practical application.To reduce the disturbance in vehicle systems,robust control[6–7]is presented.Since the design of robust control is generally based on the worst conditions of systems,the control performance can not get optimal for most situations.Nevertheless,in consider of the multiple requirements and constraints existing in the vehicle systems,model predictive control(MPC)has been introduced to these systems as an effective way to cope with such constrained optimal control problem[8].MPC is a model-based multivariable control method which aims at solving constrained control problems with optimization demands.Lots of successful papers show that MPC as a practical constrained control algorithm has been applied in many fields[9–11].Due to the nonlinear terms in vehicle stability control system,nonlinear model predictive control(NMPC)has been applied to achieve good control performance[12–13].However,there are still some problems that limit its application.For NMPC,the real-time capability should be advanced and the complexity of designing should be reduced[14].
For the past few years,some novel control schemes have been proposed to deal with the computational burden in the vehicle stability control systems using NMPC.An explicit NMPC is proposed in[15],in which the optimization problem is solved off-line.In [16–17],a fast NMPC approach is proposed using an approximated control function and derived by means of set membership (SM)techniques.In addition to the improvements in algorithm,a hardware acceleration is applied in [18]using the field programmable gate array (FPGA).However,compared with LMPC,NMPC is still not superior in computational efficiency.
In order to achieve good control performance on the basis of reducing the computational burden,an LMPC controller based on extended state observer (ESO)is proposed for yaw stability control of in-wheel-motored electric vehicle in this paper.An LMPC controller can be obtained by linearizing the two degrees of freedom(2–DOF)nonlinear vehicle model.The resulting disturbance after linearization is estimated by ESO.ESO is the key link toward the active disturbance rejection control(ADRC)proposed by HAN[19–20].It is tolerant for most uncertainties in a large degree and not a model based approach which needs accurate mathematical model[21–22].Based on the advantages above,ESO is added to the control in this paper.With the estimated disturbance compensated in the LMPC controller,the control performance is as good as NMPC approximately,and the computational efficiency is improved significantly compared to NMPC.The initial result on the LMPC controller based on ESO has been studied in our early work[23],which is for the simple single input single output system.To solve the vehicle yaw stability control problem,this paper extends it to a complicated multiple input multiple output system.The simulation results demonstrates its feasibility.
The structure of this paper is as follows.A 2–DOF vehicle model for controller design is built in Section 2.In Section 3,an LMPC controller based on ESO is designed in detail,and the stability of ESO is assessed.The simulation results and analyses are given in Section 4.Finally,the short conclusion is drawn in Section 5.
2 Modeling for controller design
In this section,the construction of 2–DOF vehicle model and tyre model are introduced respectively.
2.1 Vehicle model
Considering that the lateral and yaw motion of vehicle are related to stability closely,only these two degrees of freedom are modeled.The longitudinal speed of the vehicle is assumed to be constant.To simplify the vehicle model,the front two wheels are assumed to have same steering angle.Then the left and right wheels of each axles are lumped into a single wheel.Under the situation that drivers can only manipulate the front wheel steering,a control oriented 2–DOF vehicle model is obtained and shown in Fig.1.
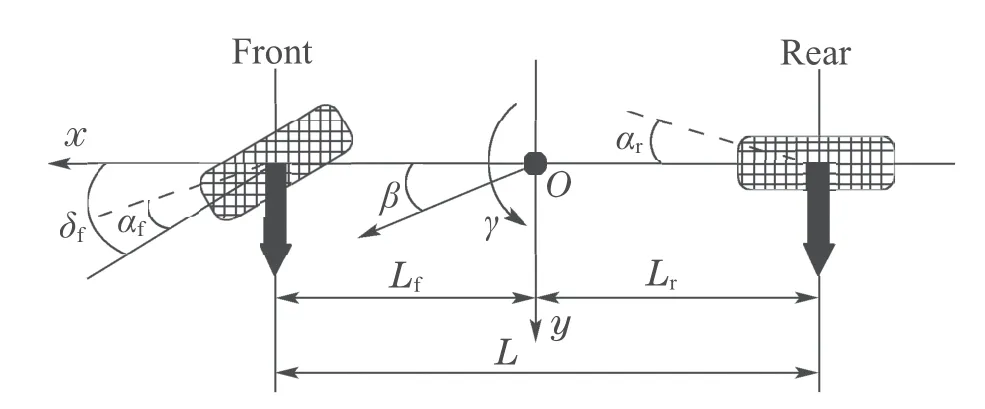
Fig.1 2–DOF vehicle model
Sideslip angleβand yaw rateγare selected as state variables.In the vehicle control system,the vehicle lateral motion and torque balance equations are as follows:
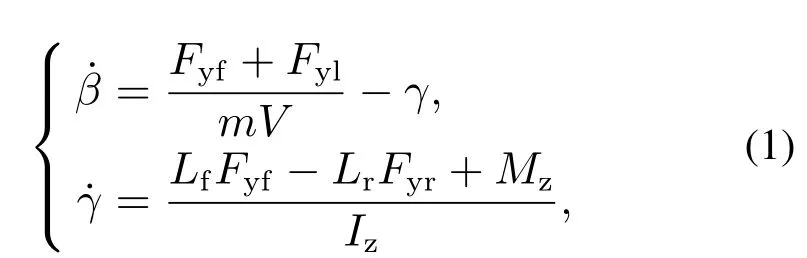
whereLfandLrare the distance from centroid to the front and rear axle respectively,Izis the moment of inertia,FyfandFylare the lateral forces of the front and rear wheels of vehicle respectively.The yaw moment of the vehicleMzcan be obtained as
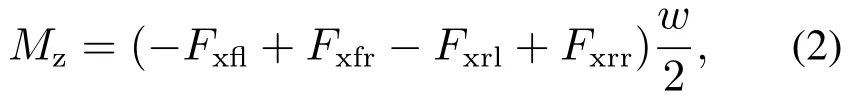
whereFxfl,Fxfr,Fxrl,Fxrrrepresent the tyre longitudinal forces,andwis the tread of vehicle.
2.2 Tyre model
Considering that the motion state of vehicle is directly determined by the comprehensive effect of tyre force,the modeling for tyre characteristics is particularly important.Among the typical tyre models,magic formula tyre model is a relatively mature one for vehicle stability control.It needs only one set of formula to realize the longitudinal and lateral simulation effects of the tyre.The magic formula is as follows:
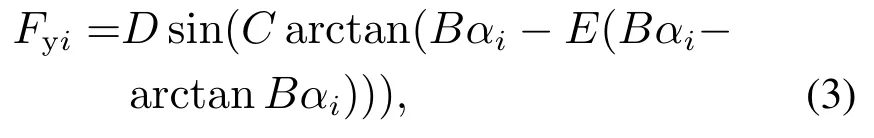
whereαiis the slip angle of tyre,andC,B,E,Drepresent the curve shape factor,stiffness factor,longitudinal stiffness and maximum factor respectively.Simplify the formula to suit the controller,then a cubic polynomial is obtained by Taylor expansion as follows:
KaandKbare obtained by tyre magic formula.According to the geometry of vehicle,the tyre sideslip angles of the front and real wheels are as follows:
In addition,although the pitch and roll motion of vehicle are not included in the vehicle modeling,their effects on the vertical load of the tyre still needs to be considered.Therefore,the vertical load of four wheels in an electric vehicle are calculated.The static loadsFzfandFzrcan be obtained as follows:
the dynamic load ?Fzfl,?Fzfr,?Fzrl,?Fzrrare calculated as follows:
whereaxandayare longitudinal and lateral acceleration respectively,his the height of center of gravity.
3 Control strategy
In this section,we will design an LMPC controller based on ESO in detail.The control requirements and schemes are introduced,and the reference model is presented.In addition,the designed ESO is proved to be stable.
The major reason for the instability of vehicle is that the tyre cannot provide sufficient steering centripetal force when the lateral force is saturated.The yaw rate and sideslip angle of the vehicle are two important variables describing the vehicle posture,which are related to vehicle stability closely.The yaw rate reflects the steady-state turning characteristics,and the sideslip angle reflects the stability of the vehicle.When the sideslip angle is relatively small,the turning speed and turning radius of vehicle are mainly determined by the yaw rate.On the contrary,it will become the main factor which changes the slip angle of tyre.Therefore,in the vehicle yaw stability control system,the main control target is to make the vehicle yaw rate track the desired yaw rate and the sideslip angle as close to zero as possible.A control structure of the vehicle yaw stability system is shown in Fig.2.
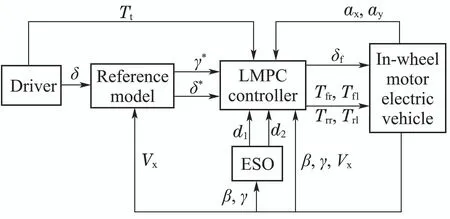
Fig.2 Control structure of vehicle yaw stability system
As the control structure diagram shows,the driver module is responsible for simulating the driver’s driving operation,and providing the steering wheel angle and the driver’s desired torque.The vehicle reference model determines the desired yaw rate and sideslip angle according to the steering wheel angle given by driver.Two disturbance signals are generated after linearization,and the disturbance observer is regarded as a multivariable ESO to compensate its real-time estimation to the linear controller.ESO is combined with LMPC controller as the overall controller of the system to provide the front wheel angle and the driving torque of four wheels.
3.1 Reference model
Since this paper studies on the integrated control system of active front steer(AFS)and direct yaw control(DYC),the reference model is described as follows:
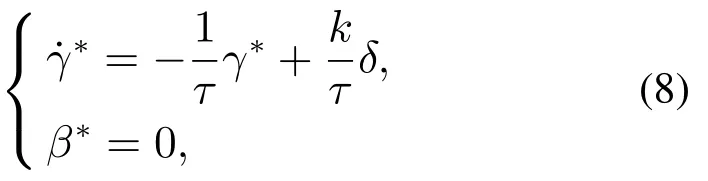
kandτare as follows:
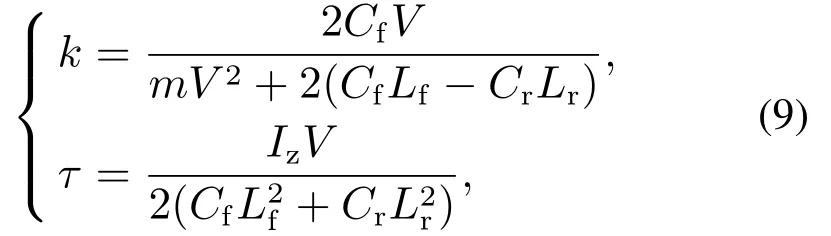
whereδis steering wheel angle,CfandCrare the cornering stiffness for front and rear wheel respectively,Vrepresents the vehicle longitudinal speed,mis vehicle mass andIzrepresents the moment inertia.
3.2 LMPC controller design
Considering that the yaw rate and sideslip angle are closely related to the vehicle yaw stability,they are chosen as the state variablesx=[β γ]T.Given that the drive unit contains four in-wheel motors and active steering devices,the front wheel steering angle and motor torque act as control inputsu=[δfTxflTxfrTxrlTxrr]T.Moreover,the state variables are also selected as the output variablesy=[β γ]T.It is assumed that the output variablesβandγcan be obtained by measurement or estimator.
Given that the vehicle yaw stability control system belongs to nonlinear system and the nonlinearity is mainly reflected in the lateral force of tyre as Equation(4)presents,it is necessary to make the linearization for LMPC design.Neglecting the nonlinear terms in Equation (4)directly,the linear expression of lateral force can be obtained as Equation(10).The disturbance term is defined asd=[d1d2]T,which represents the part estimated by ESO after the linearization.
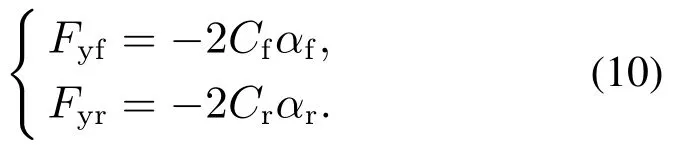
As the system model introduced in Section 2,the continuous-time model is obtained as follows:

To reduce static error,the continuous-time model is converted into incremental model during the process of discretization by Euler method:
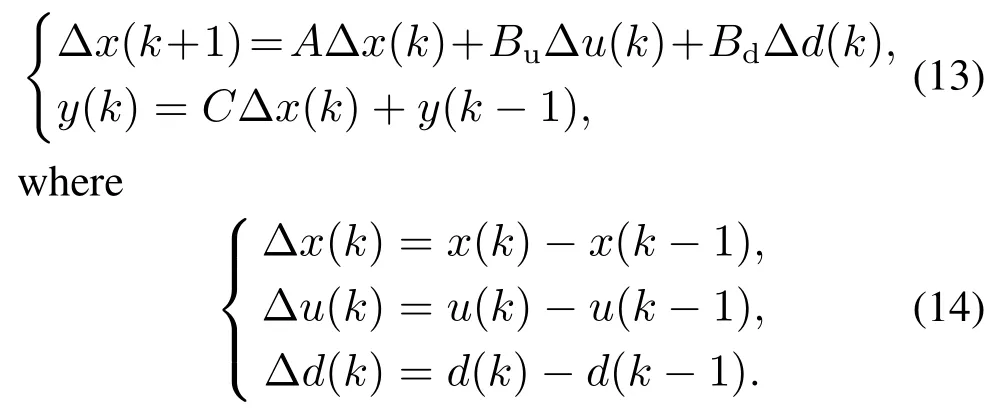
According to the MPC’s principle,mis defined as control horizon andpis defined as predictive horizon,mp.In this paper,vehicle velocity and disturbances estimated by ESO are supposed to be constant in predictive horizon.Based on the model described in Equation(13),incremental sequence of control input inpstep at timekis obtained as follows.It is chosen as an independent variable for constrained optimization problems:
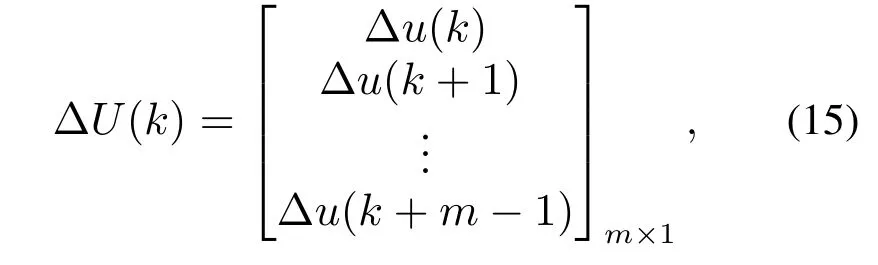
the predicted control output sequence is written as
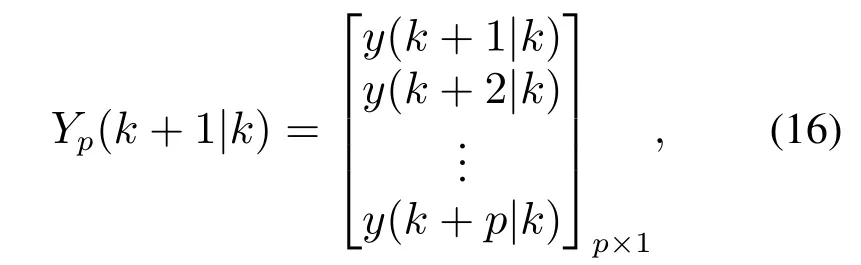
it can be calculated as
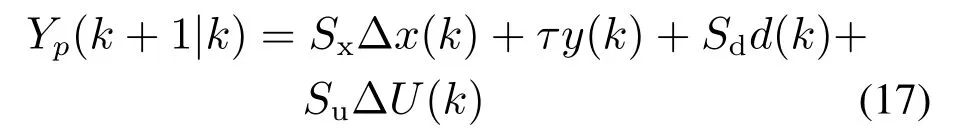
whereSx,SdandSucan be derived from the coefficients of Equation(13).
Moreover,according to the reference model introduced in Section 2,the control output reference sequence is obtained as

In consideration of control requirements,the outputYpis supposed to track the reference sequenceRclosely to achieve vehicle yaw stability.Therefore,the deviation between them should be minimized as much as possible,and the first cost function is obtained as
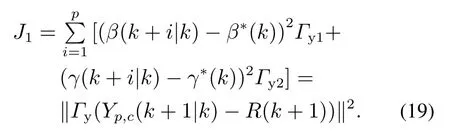
From another perspective,the second cost function is obtained to achieve smooth control.
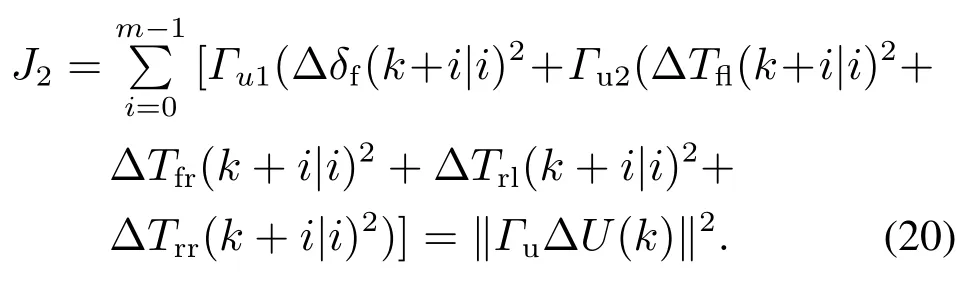
Furthermore,in order to minimize the energy consumption and the longitudinal force of tyre under the constraints,the third cost function can be obtained as
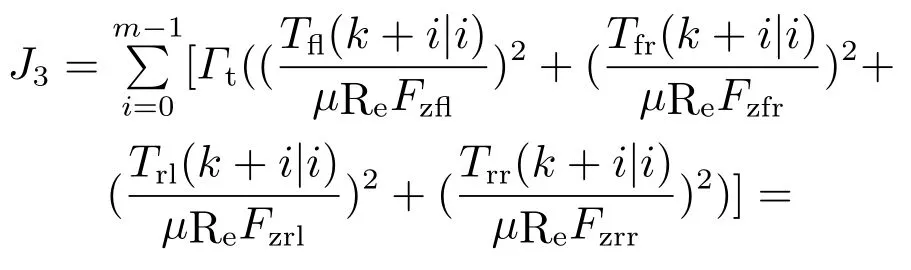
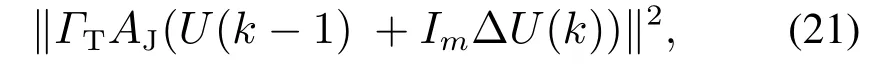
whereμ,ReandFzjare the friction coefficient,wheel radius and vertical load of the four wheels introduced in Section 2,andFzjare constant in the predictive horizon.Through the derivation,AJ,ImandΓTcan be obtained as follows:
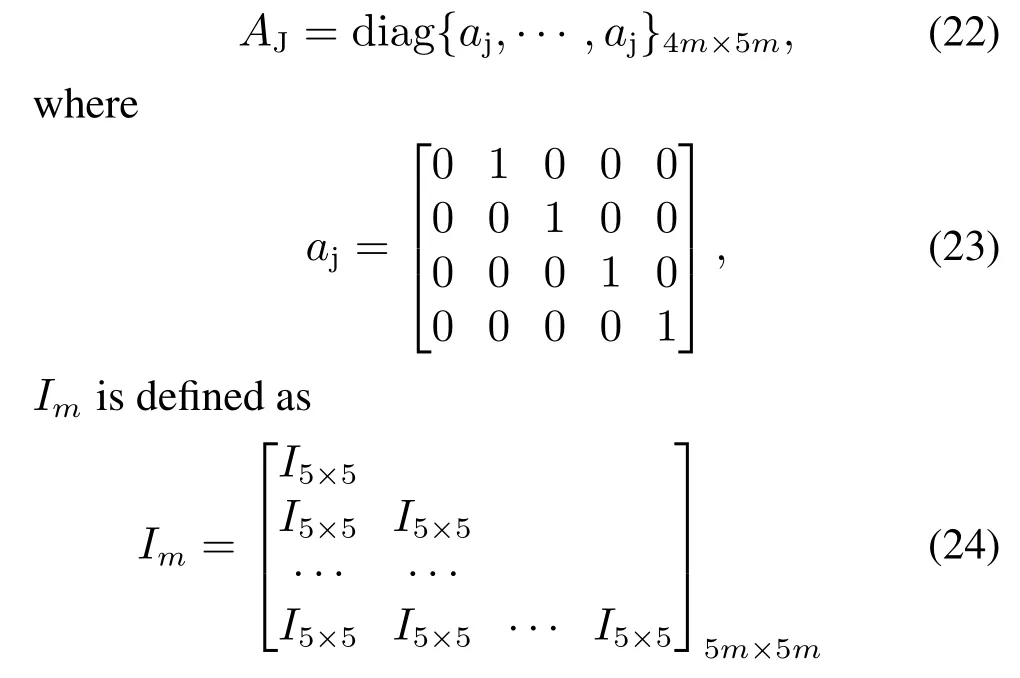
as forΓT,definethen we can obtain thatΓT=diag{ΓT1,ΓT2,ΓT3,ΓT4}.
Considering that MPC can deal with multiobjective optimization control problem,the three parts mentioned above can be integrated as
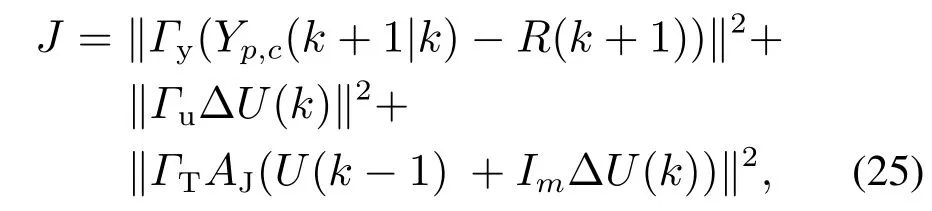
whereΓy,ΓuandΓTare weighting matrixes that can be used to adjust the control performance.Ignore the items which not related to ?U(k),the equivalent form of the optimization is obtained as
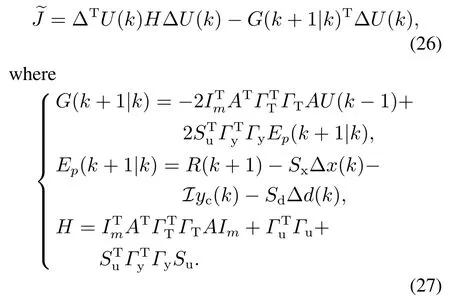
In addition,aiming at achieving desired control performance,the constraints should be considered in the design of MPC.Due to motor torque saturation,the system had better satisfy the following constraint:
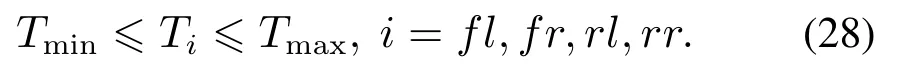
Simultaneously,the sum of torques for each motor are supposed to be equal to the total required one as follows:
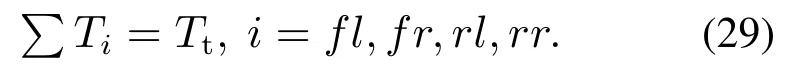
3.3 ESO Design
Owing to the plant-model mismatch caused by model linearization(Equation(10)),ESO is designed to capture the plant-model mismatch and external disturbance.Then the estimated disturbance is compensated in the LMPC controller to obtain a better performance.
For vehicle yaw stability control system in this paper,two disturbance variablesd1andd2in the linear predictive model are supposed to be extended into two new state variablesω1=d1andω2=d2to form the extended system as follows:
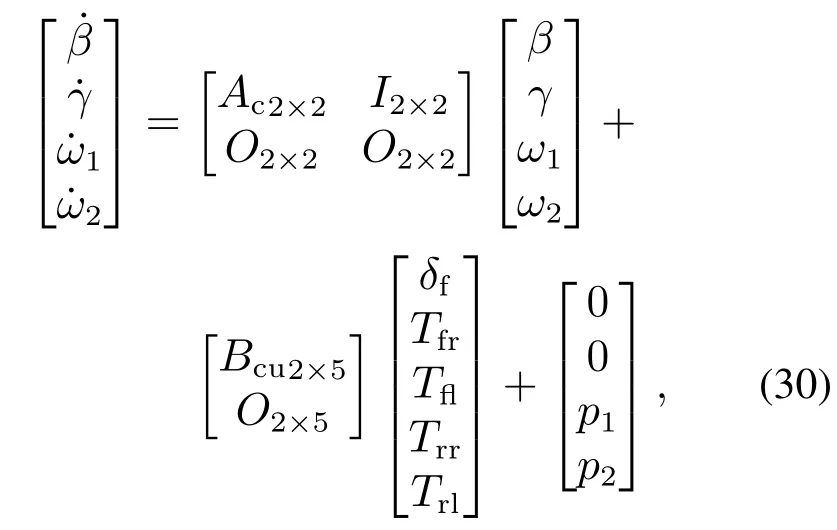
whereAc,Bcuare obtained by incremental model as Equation(11).In order to ensure the convergence of the observer,assume that ˙ω1=p1and ˙ω2=p2are both bounded by constant.For the extended linear predictive model,the following form of multi-variable ESO is designed.
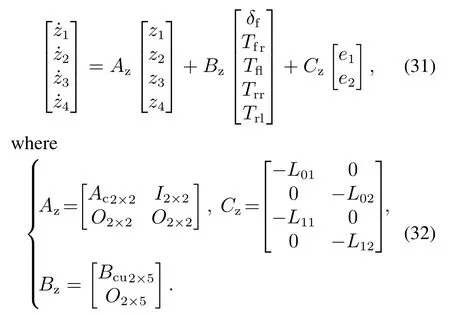
For the multi-variable ESO designed above,we can obtain thatz1,z2,z3andz4are dynamic estimations ofβ,γ,d1andd2respectively.Define the dynamics of the estimate error as
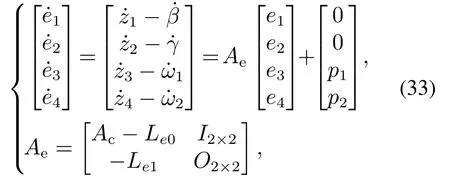
whereLe0=diag{L01,L02},Le1=diag{L11,L12}.As long asAeis chosen to be Hurwitz matrix,the dynamics of the estimate error is input-to-state stable forp1andp2.
Remark 1The related works of disturbance observer based MPC was reported in[24–27],which utilizes numerical solutions in the optimization problem.The offset-free MPC by augmenting the system with disturbance model was studied in [24]and [25]for linear systems,in [26]for nonlinear systems,and in [27]for reference tracking problems.These works took the disturbance estimation and its prediction into account in the receding optimization process and achieved zero offset.The recursive feasibility of the optimization problem was guaranteed by tightening the terminal region and the input constraint was studied in[28]for tracking the wheeled mobile robot.Based on aforementioned methods,the stability analysis of the combination of LMPC and ESO will be our future work of the paper.
4 Simulation
In this section,the simulation results in Simulink/MATLAB are presented to verify the method proposed in this paper.A seven degrees of freedom(7–DOF)vehicle model including the yaw of longitudinal,lateral and vertical of the vehicle and the rotation of 4 wheels is built on the simulation platform as follows in Fig.3.The specific model parameters are shown in Table 1.
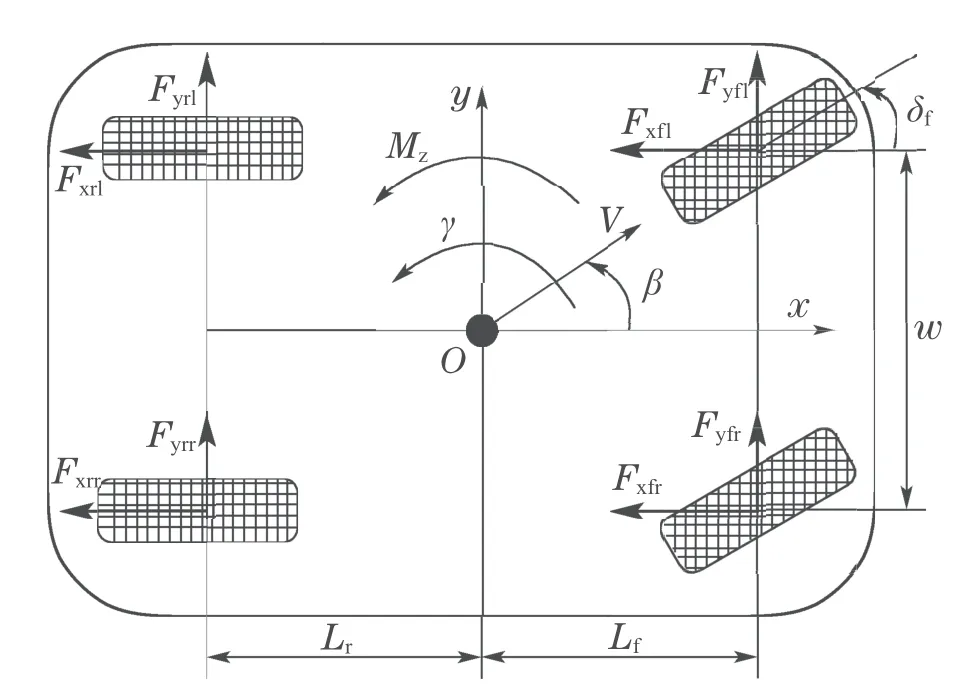
Fig.3 7–DOF vehicle model
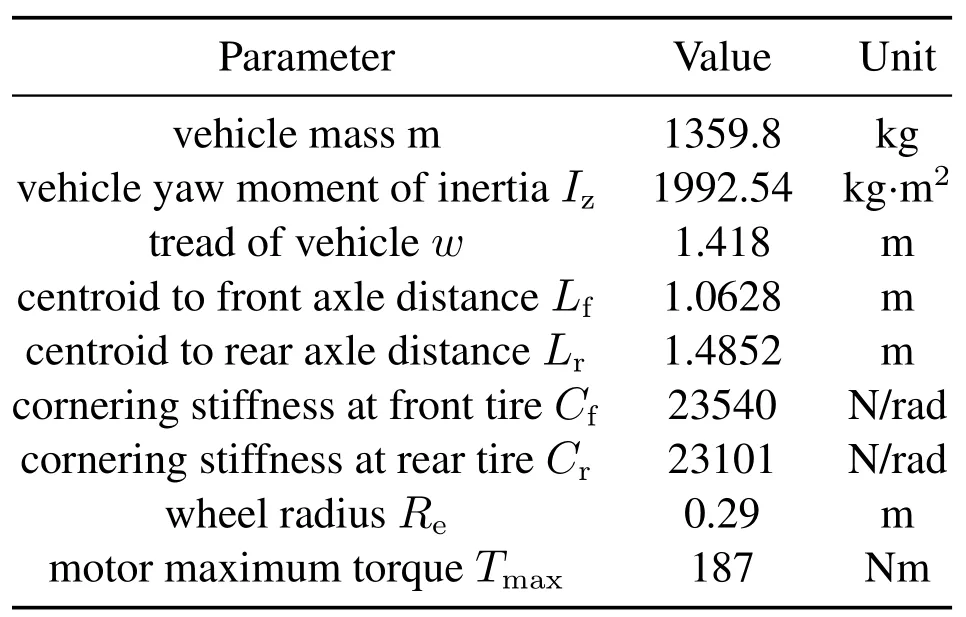
Table 1 Model parameters
The reference steering wheel input curve is given in Fig.4.Set the sampling time to 10 ms.The predictive horizonpand control horizonmare equal to 10 and 3 respectively.As for the observer parameter,they are set asL01=20,L02=40,L11=100,L12=200,then it satisfies the condition thatAeis Hurwitz matrix.
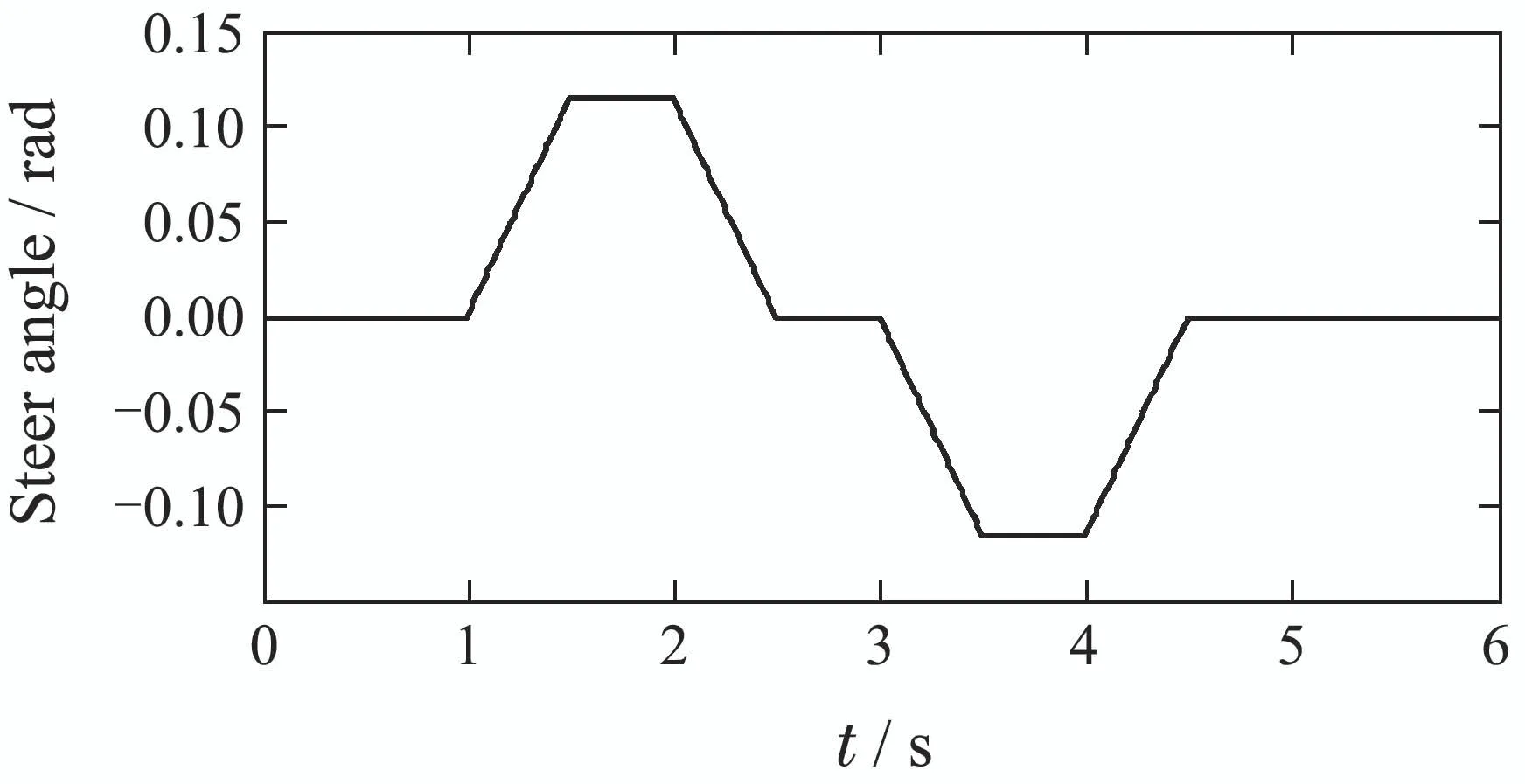
Fig.4 Steer input curve
For different driving maneuvers,the effectiveness of the controller is analyzed.In the first maneuver,the initial speed is 80 km/h,and friction coefficient is set to 0.8.The designed LMPC controller based on ESO is applied to the vehicle yaw stability control system as shown in Fig.5.In addition,the result of an NMPC controller is presented for comparison in Fig.6.
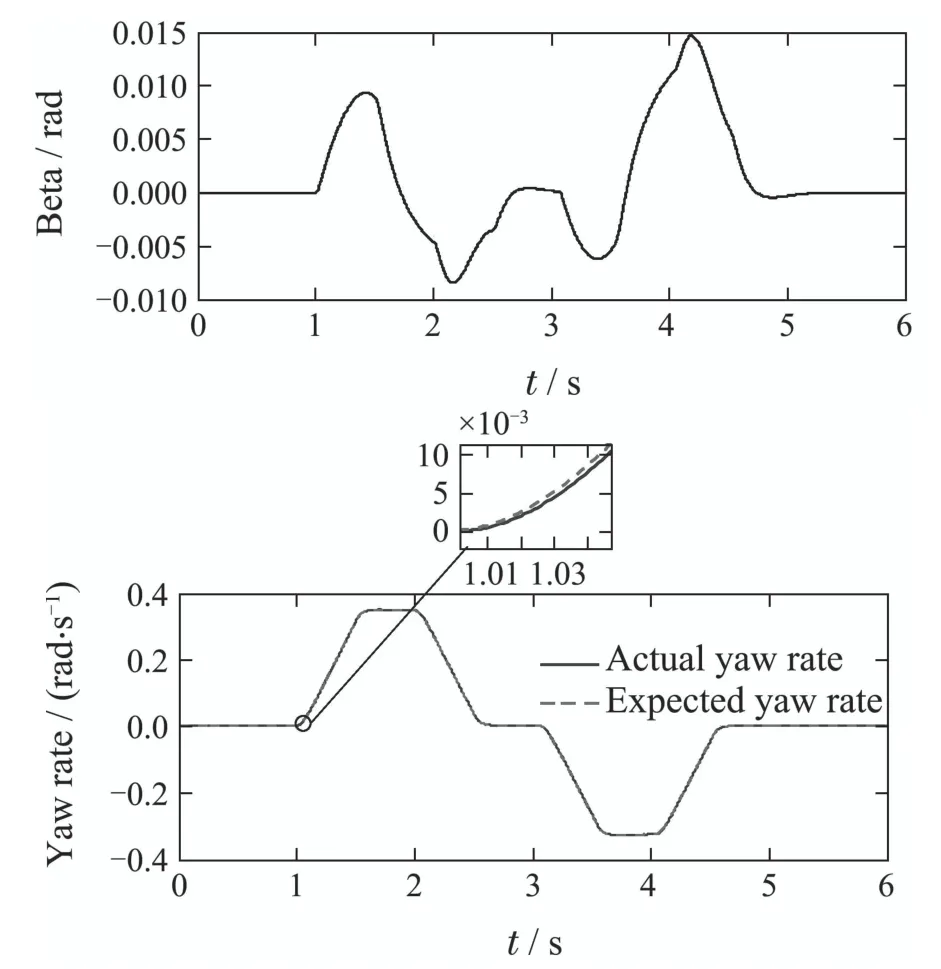
Fig.5 Simulation results of LMPC based on ESO whenμ=0.8
In each figure,dashed line represents the expected output of system,and the solid one represents the actual output.The comparison shows that the performance of the two controllers are basically the same.On the basis of analysis,it is shown that the tyre lateral force is in the linear area consistently in this maneuver.
To excite the nonlinearity of the lateral tyre force,the friction coefficient is changed to 0.4 as the second maneuver.Then the simulation results form two controllers are presented in Figs.7–8.
Comparing the control performance of LMPC controller based on ESO with NMPC controller,it can be obtained that they are basically the same although in such nonlinear situation.Furthermore,in order to compare the tracking performance more obviously,the error curves between expected yaw rate and the actual one are presented in Fig.9.
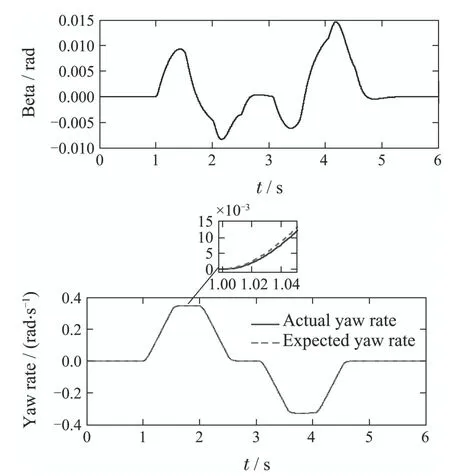
Fig.6 Simulation results of NMPC whenμ=0.8
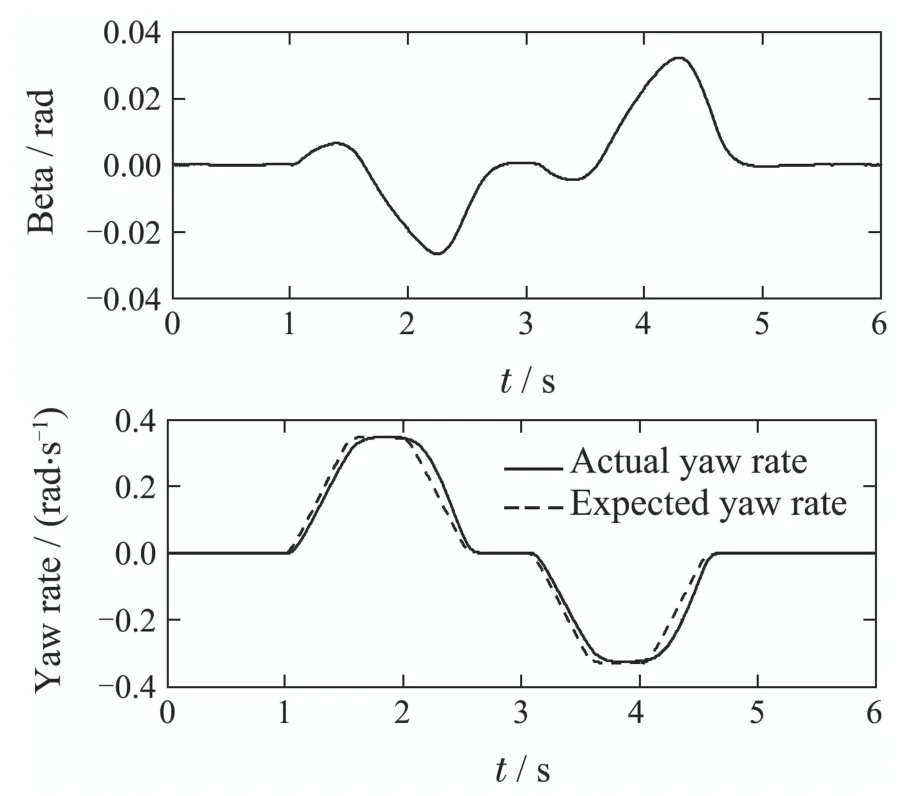
Fig.7 Simulation results of LMPC based on ESO whenμ=0.4
From the error curves,it proves that the proposed LMPC based on ESO control strategy has the ability to improve the control performance compared to LMPC.What is even more exciting is that this strategy can achieve as good control performance as NMPC.In addition,to make the comparison more intuitively,the standard deviation of each controller is calculated as follows:
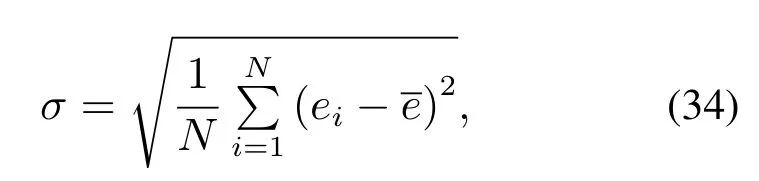
whereei=γi??γi.
After the calculation,the standard deviations from these three controllers are obtained successively.The results of LMPC,NMPC and LMPC based on ESO are 0.0287,0.0237 and 0.0238 in turn.
In the case of first maneuver,the lateral tyre force is always in linear area,so that the predictive model is basically a linear model.Nevertheless,in the case of second maneuver,the friction coefficient is reduced,and it leads the vehicle to a limit maneuver during the operation,then the lateral tyre force gets the nonlinear term occurred as a result.In this situation,single LMPC can not track the desired yaw rate well and make the sideslip angle close to zero.By contrast,the LMPC controller based on ESO proposed in this paper can basically achieve the control performance consistent with NMPC controller.Owing to the fact that the plant-model mismatch and external disturbance can be captured and compensated in the LMPC controller,the control performance is improved by using a disturbance feedforward control.However,this strategy proposed in this paper is only applicable to the weakly nonlinear systems with slow changing disturbances.
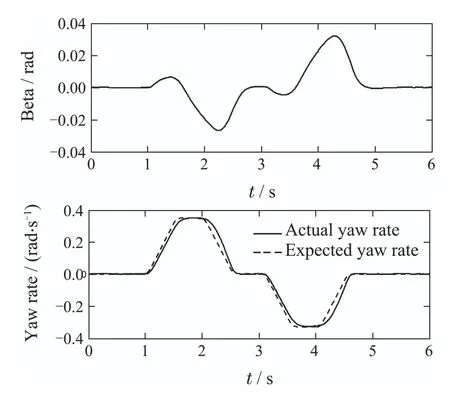
Fig.8 Simulation results of NMPC whenμ=0.4
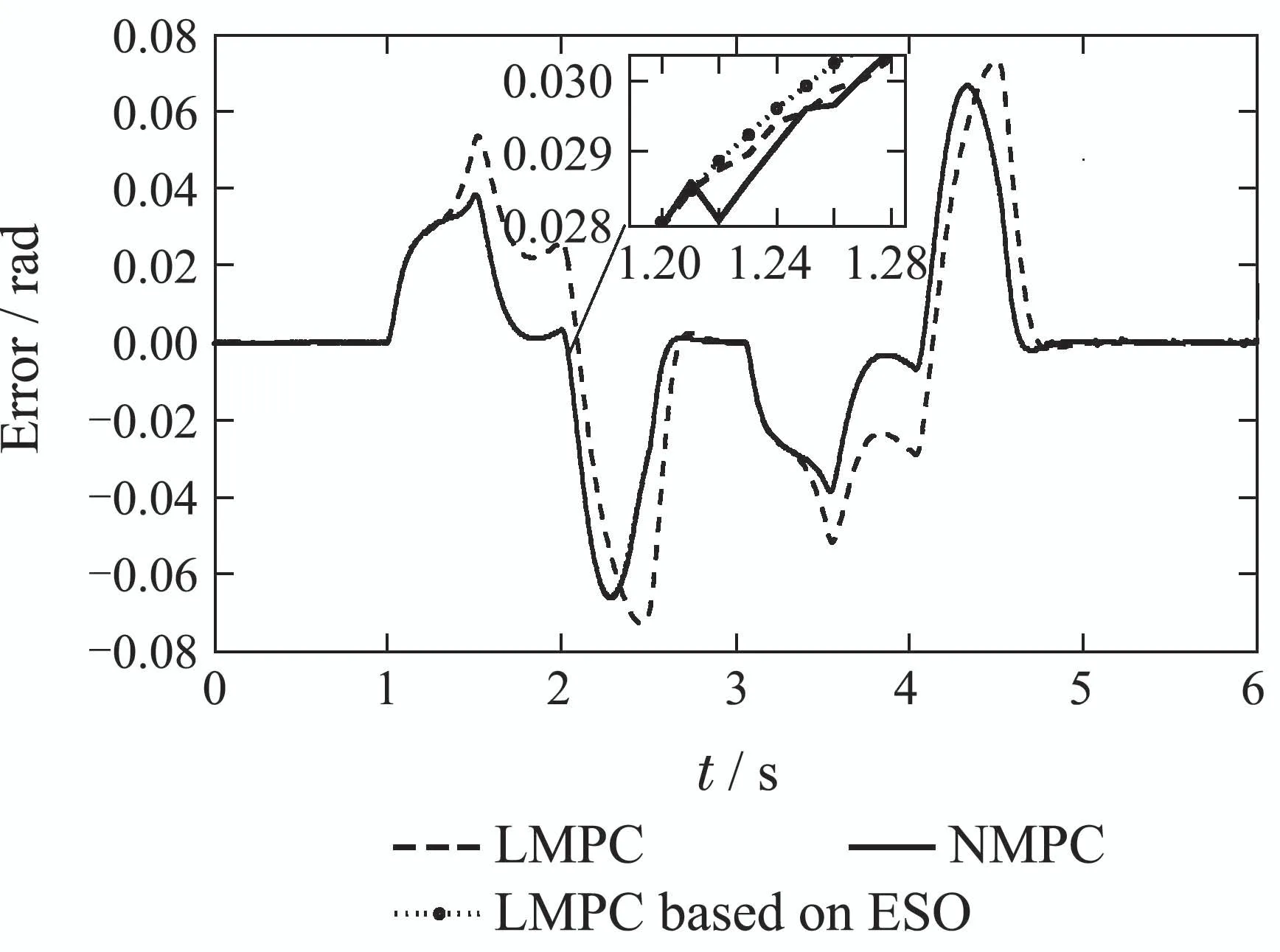
Fig.9 Tracking error with friction coefficient 0.4 by LMPC,NMPC and LMPC based on ESO
In order to verify the advantages of the method proposed in this paper in computational performance,the comparison results of the solution time on MATLAB platform of LMPC based on ESO and NMPC are presented as shown in Fig.10.The simulation platform is configured as 64–bit Windows 7 PC (CPU Intel Core i7–4790@3.60 GHz,8 GB memory),MATLAB2014a.
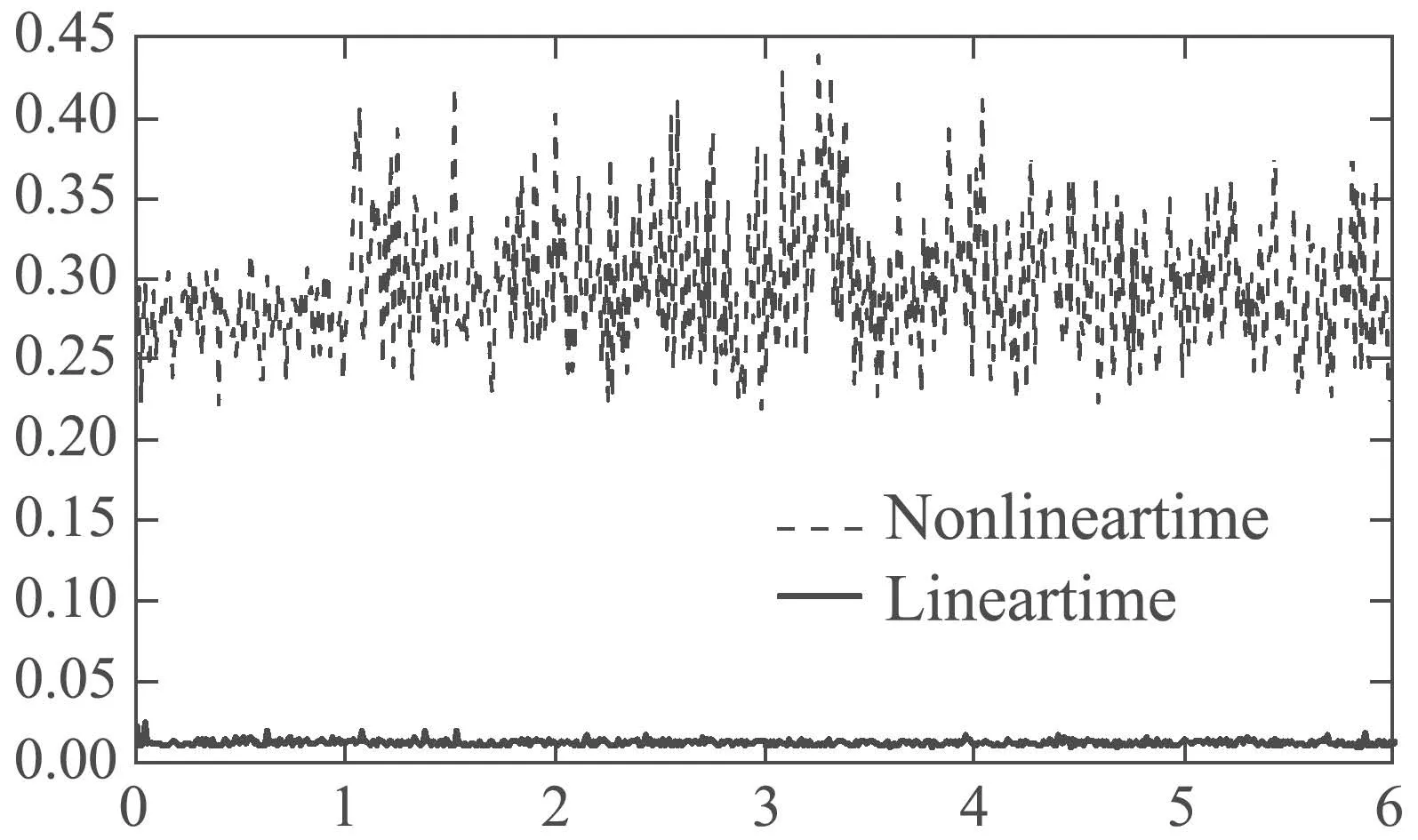
Fig.10 The comparison results of solution time
The results show that the time of solving one optimization problem using NMPC is about 0.35 s,while it is about 0.025 s using LMPC based on ESO.It can be seen that computational time can be greatly reduced on the premise of ensuring consistent control performance.
5 Conclusion
A novel method of LMPC controller based on ESO is proposed for vehicle yaw stability control system in this paper,which can reduce the computational burden to some extent compared to NMPC controller in practical application.ESO is used to estimate the disturbance to compensate modeling error caused by linearization,and its stability is proved simultaneously.The simulation results demonstrate that the nonlinear term would appear when the vehicle is approaching extreme conditions.At this time,ESO-based LMPC can meet the control requirements as NMPC.The sideslip angle is close to zero,and the yaw rate can track its reference value well,which satisfy the control requirements effectively.

