ULAM-HYERS-RASSIAS STABILITY AND EXISTENCE OF SOLUTIONS TO NONLINEAR FRACTIONAL DIFFERENCE EQUATIONS WITH MULTIPOINT SUMMATION BOUNDARY CONDITION?
Syed Sabyel HAIDER Mujeeb Ur REHMAN
School of Natural Sciences,National University of Sciences and Technology,H-12 Islamabad,44000,Pakistan
E-mail:rediahleybas@gmail.com;mujeeburrehman345@yahoo.com
Abstract The purpose of this study is to acquire some conditions that reveal existence and stability for solutions to a class of difference equations with non-integer orderμ∈(1,2].The required conditions are obtained by applying the technique of contraction principle for uniqueness and Schauder’s fixed point theorem for existence.Also,we establish some conditions under which the solution of the considered class of difference equations is generalized Ulam-Hyers-Rassias stable.Example for the illustration of results is given.
Key words Fractional difference equation;Green’s function;existence and uniqueness;Ulam-Hyers-Rassias stability;summation boundary condition
1 Introduction
The subject of discrete fractional calculus has got the attention of several researchers.Atici et al.[1,2],Anastassiou[3],Abdeljawad et al.[4,5],and Cheng[6,7]are among pioneer of work in this area.For difference equations,Bohner and Peterson treat the dynamic equations on time scales in[8]and get surprisingly different results from continuous counterpart.In 1988,Gray and Zhang[9]introduced a type of fractional difference operator,and they presented a Leibniz rule,a composition formula and a power law for differences.However,they dealt exclusively with the nabla(backward)difference operator and therefore offer results distinct from present results,where the delta(forward)difference operator is used exclusively.A rigorous intrigue in fractional calculus of differences was exhibited by Atici and Eloe,and they explored characteristics of falling function,a new power law for delta difference operators and the commutativity of sums and differences of arbitrary order.They also presented advance composition formulas for sums and differences of non-integer order in[2].For non-integer order,changes in the domain of function to sums and differences are an important aspect which got special attention by Atici and Eloe in[2,10]for a rigorous and correct dealing of the fractional composition formulas.
Fractional difference equation is a growing area of the research and existence concept of solution for delta difference system of arbitrary order with boundary conditions was examined broadly by a lot of researcher;for instant,we refer a few of them[11–32].The majority of researcher considered fractional difference equations with an extensive variety of boundary conditions,meanwhile among others Reunsumrit,Kaewwisetkul and Sitthiwirattham considered sum boundary conditions with two and three points in[28,29,33,34].However,Goodrich[35]considered multi-point sum boundary conditions with growth.
The mathematical models of many real world phenomena can be represented by multi-point boundary value problems.Such models have a large numbers of applications in numerous areas of modeling and analyzing problems which often arise from electric power networks,electric railway systems,elasticity,thermodynamics,telecommunication lines,wave propagation and for analyzing kinetical reaction problems;for details,see[36]and references therein.Another reason of studying discrete problem is the discrete nature of the solution which amends during the discretization process of continuous boundary value problem.Moreover,two point boundary value problems in continuous setting lead to multi-point in the discrete setting;a detailed discussion by Agarwal can be found in[37].
The idea of Ulam-Hyers type stability is important to both functional and applied problems;especially in biology,economics,and numerical analysis.It may have potential application in nonlinear analysis including difference and summation equations.Rassias[38]introduced continuity condition which produced an acceptable stronger results.In the continuous setting extensive work on Ulam-Hyers-Rassias stability for non-integer order differential equation has been done.However,in discrete fractional setting,a limited work can be found in[13,39].Interested reader may find the detailed literature on Ulam-Hyers-Rassias stability in[38,40–42].To the authors knowledge,neither the existence nor the Ulam-Hyers-Rassias stability of the solution to the considered class of multipoint fractional boundary value problem(MPFBVP)has been studied.
Here,we shall study the existence and Ulam-Hyers-Rassias stability for the given nonlinear difference equation of non-integer order with multi-point summation boundary conditions.
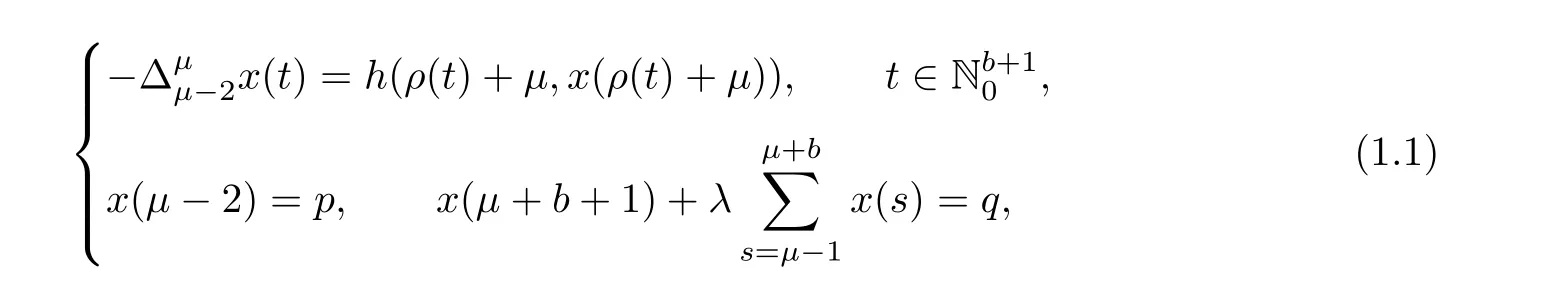
This article is organized in five sections.We state a few basic but important definitions and results from discrete calculus in preliminaries section.In Section 3,we shall derive Green’s function with some of its properties.Existence condition and uniqueness condition of solutions will be acquired in Section 4.Conditions for Ulam-Hyers and Ulam-Hyers-Rassias stability will be obtained in Section 5.
2 Preliminaries
For convenience,this section comprise of some basic definitions and results for later use in the following sections.The functions we will consider are usually defined on the set Na:={a,a+1,a+2,···},:={a,a+1,a+2,···,b},and[a,b]Na:=[a,b]∩ Nafor fixed a,b ∈ R[43].The jump operators σ(t)=t+1 and ρ(t)=t? 1 are forward and backward,respectively,for t∈ Na.The ceiling functionmaps a real number to the smallest following integer.The following concept are discussed in[8,44].
Definition 2.1The falling function in term of gamma function is given by

given that the expression in above equation is justifiable.It is convenient to take tμ=0,whenever t+1 is natural number and t?μ+1 is zero or negative integer.
Definition 2.2Theμthorder Taylor monomial is defined by
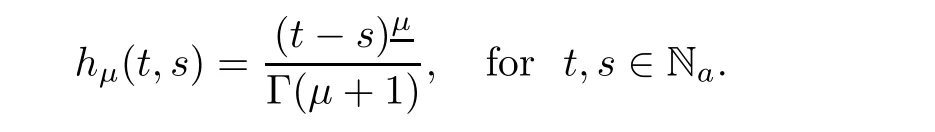
Definition 2.3Assume that g:Na→R andμ>0.Then,theμthdelta sum of g is given by
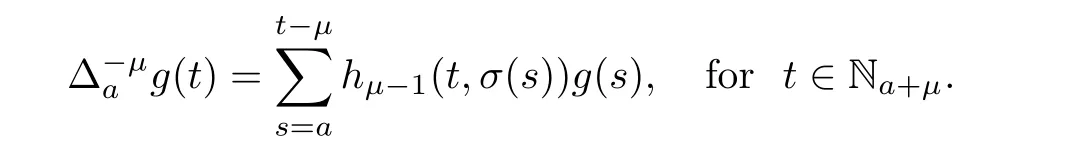
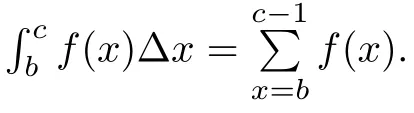
Lemma 2.5Assume g1,g2:Then,for
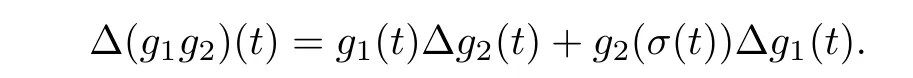

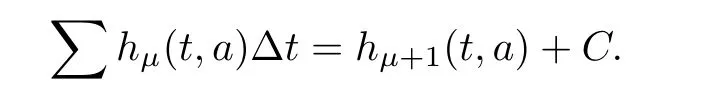
Lemma 2.7(Fundamental theorem) Suppose thatand anti-difference of h onis H.Subsequently,

Lemma 2.9Let r be a positive integer such that r?1<μ≤r.If g:N0→R,then the problem

has the solution represented by
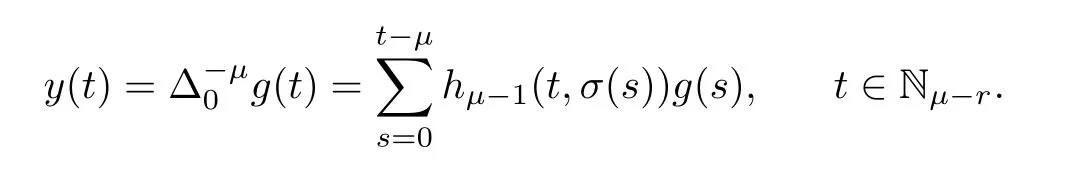
The definitions of Ulam stability for fractional difference equations was introduced in[13].Consider system(1.1)and the following inequalities:
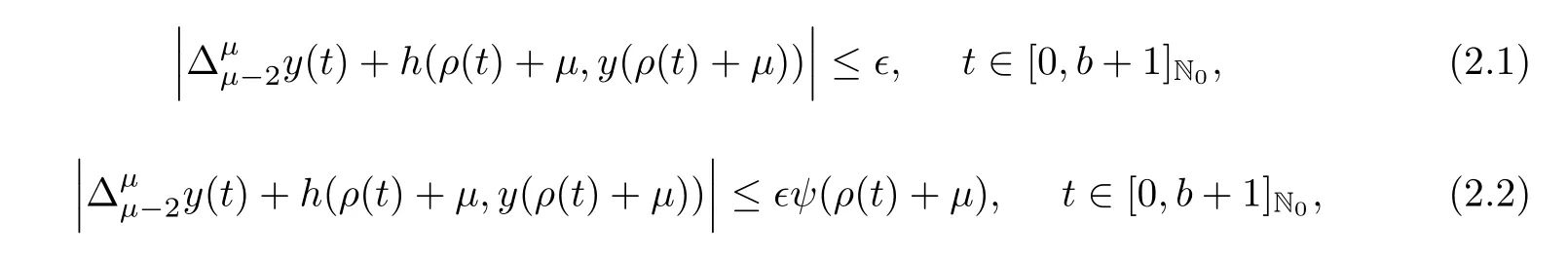
Definition 2.10If there exists a real number dh>0 such that for eachand for every solution y(t)∈K of inequality(2.1),then a solution x(t)∈K of system(1.1)is Ulam-Hyers stable if it satisfies
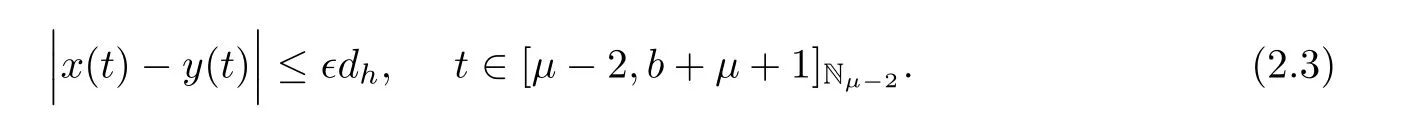
The solution of system(1.1)is generalized Ulam-Hyers stable if we substitute the function φh(?)for the constant ?dhin inequality(2.3),where φh(?) ∈ C(R+,R+),and φh(0)=0.
Definition 2.11If there exists a real number dh,ψ>0 such that for each ?>0 and for every solution y(t)∈K of inequality(2.2),then a solution x(t)∈K of system(1.1)is Ulam-Hyers-Rassias stable with respect to function ψ if it satisfies
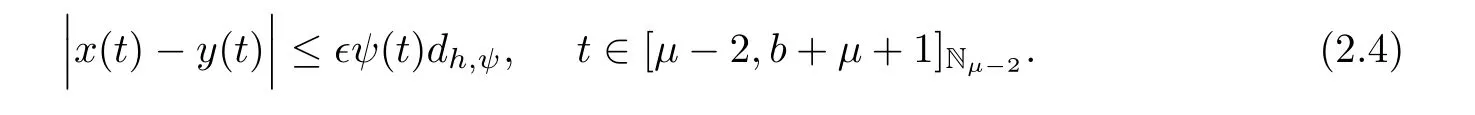
The solution of system(1.1)is generalized Ulam-Hyers-Rassias stable if we substitute the function Φ(t)for the function ?ψ(t)in inequalities(2.2)and(2.4).
3 Green’s Function for MPFBVP With Summation Condition
In this section,our purpose is to obtain Green’s function for MPFBVP(3.1),further the maximum value of its sum is acquired for later to use in upcoming section.
First,we examine the non-homogeneous MPFBVP with summation conditions:
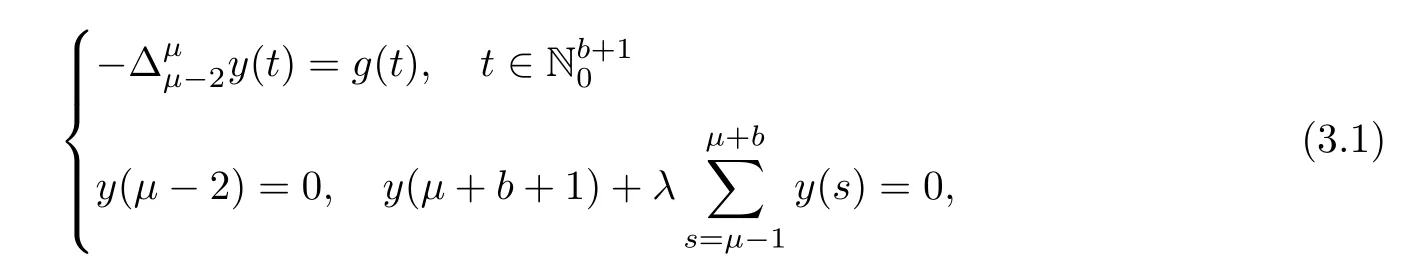
Theorem 3.1The solution y of the MPFBVP(3.1)is given by
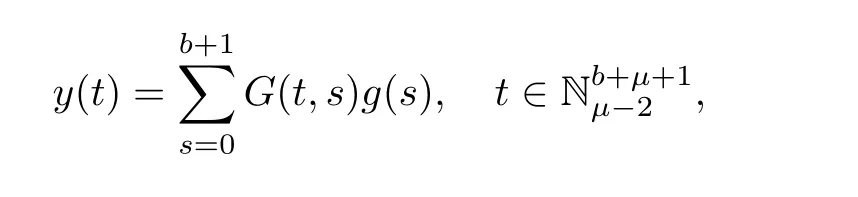
with G(t,s)stated as
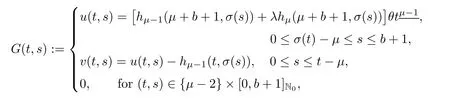
ProofSuppose that y onsatisfy the equation
By making use Lemmas 2.8 and 2.9,we get
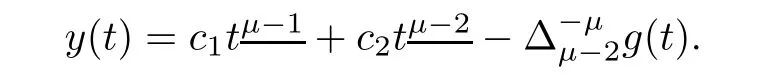
Definition 2.3 implies that
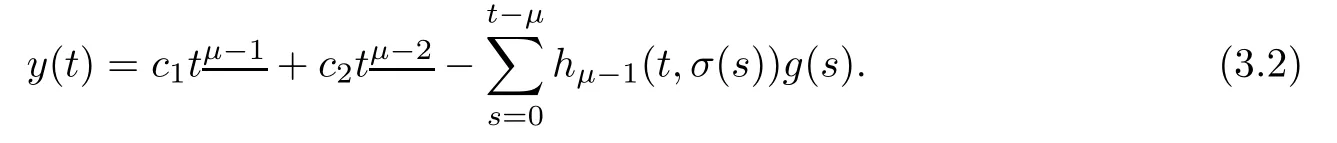
Using the first boundary condition y(μ?2)=0,we have
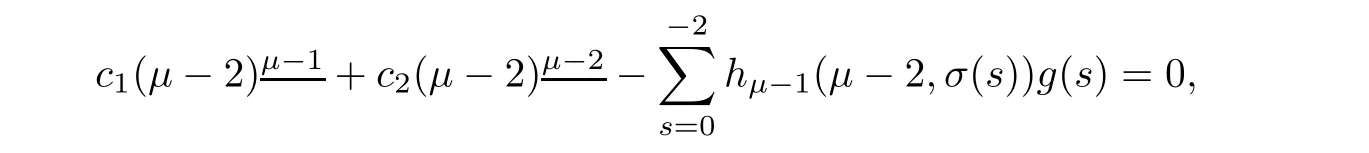
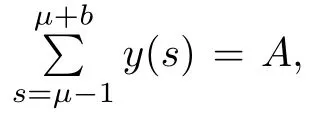
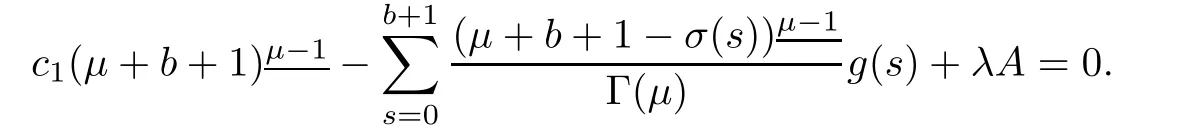
Solving for c1,we have
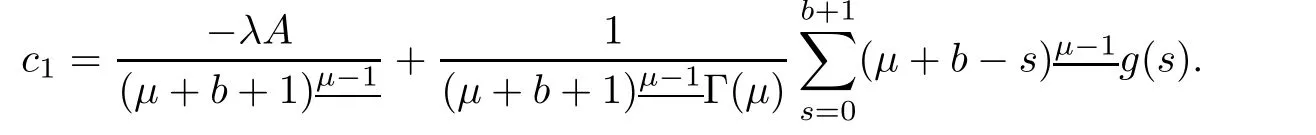
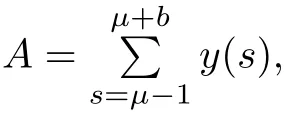
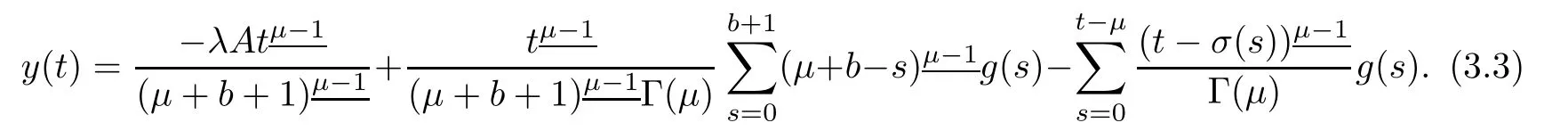
To evaluate A,using y in we have
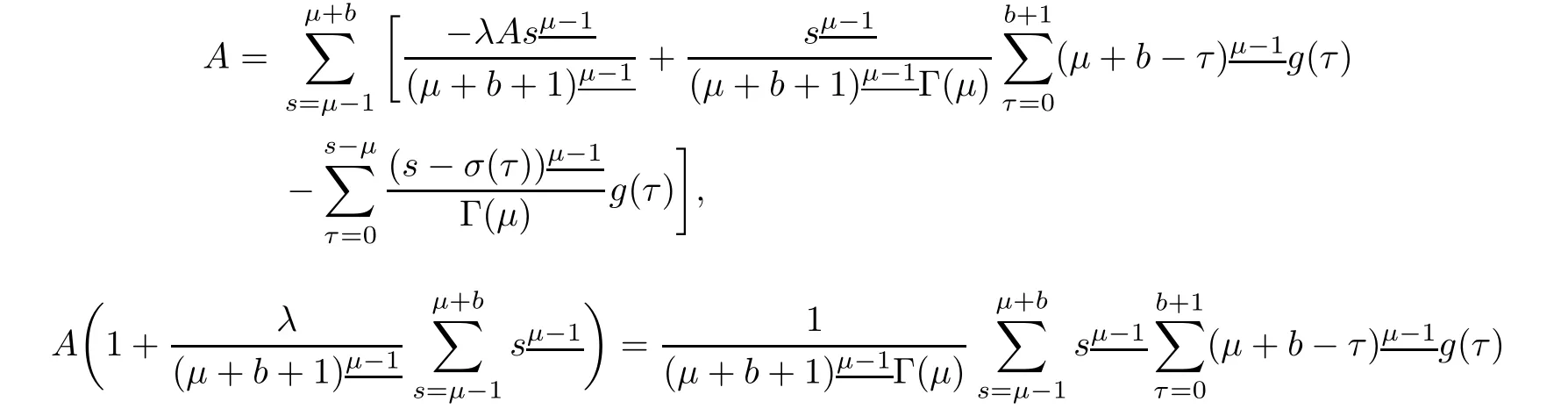
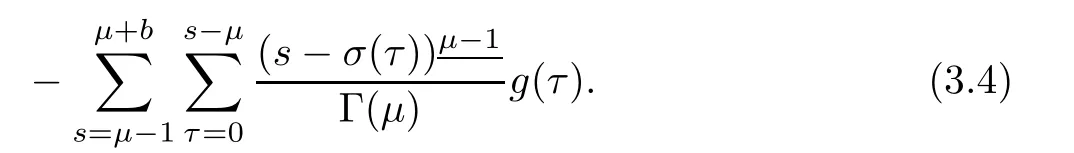
Changing in order of summation in the last double sum of equation(3.4),we have
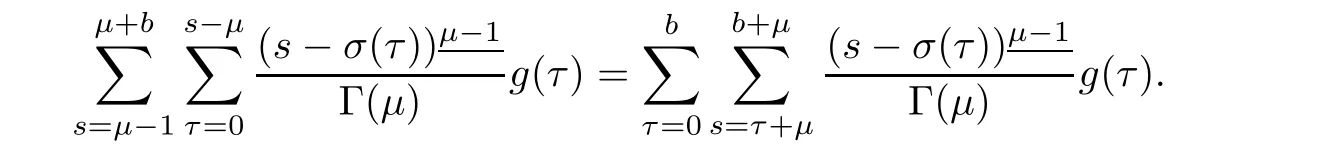
Making substitution s=x+ σ(τ)only for inner sum and then using Lemmas 2.6 and 2.7
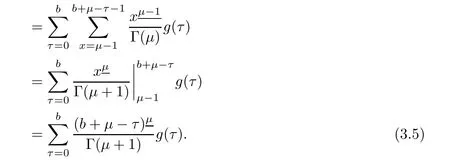
As sums are independent in the first double sum of equation(3.4),use Definition 2.2,Definition 2.4,Lemma 2.6,and Lemma 2.7 to evaluate the sum
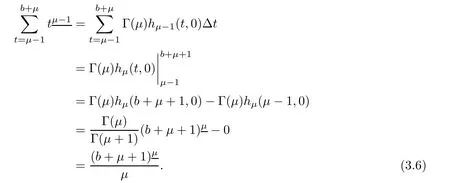
Making use of equations(3.5),(3.6)in equation(3.4),we obtain
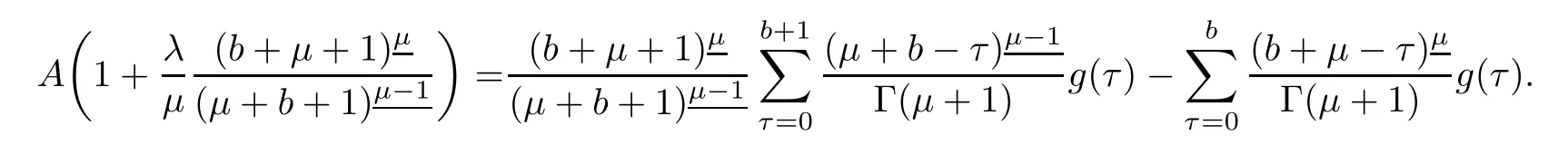
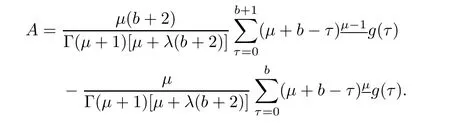
Putting value of A in equation(3.3),we have
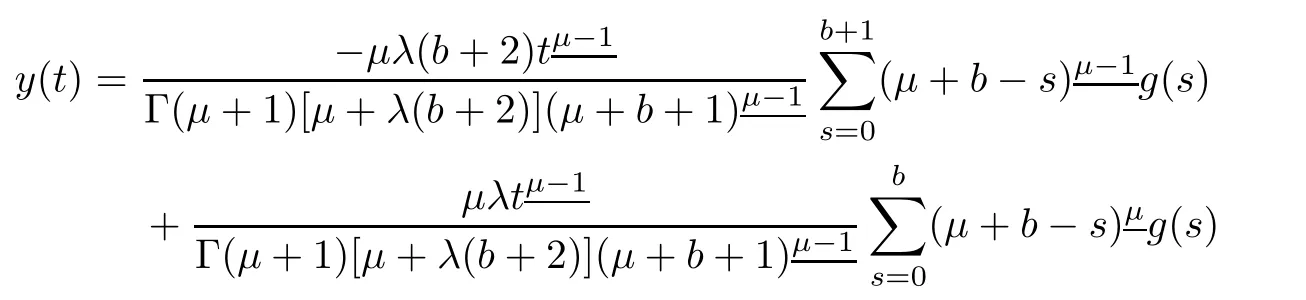
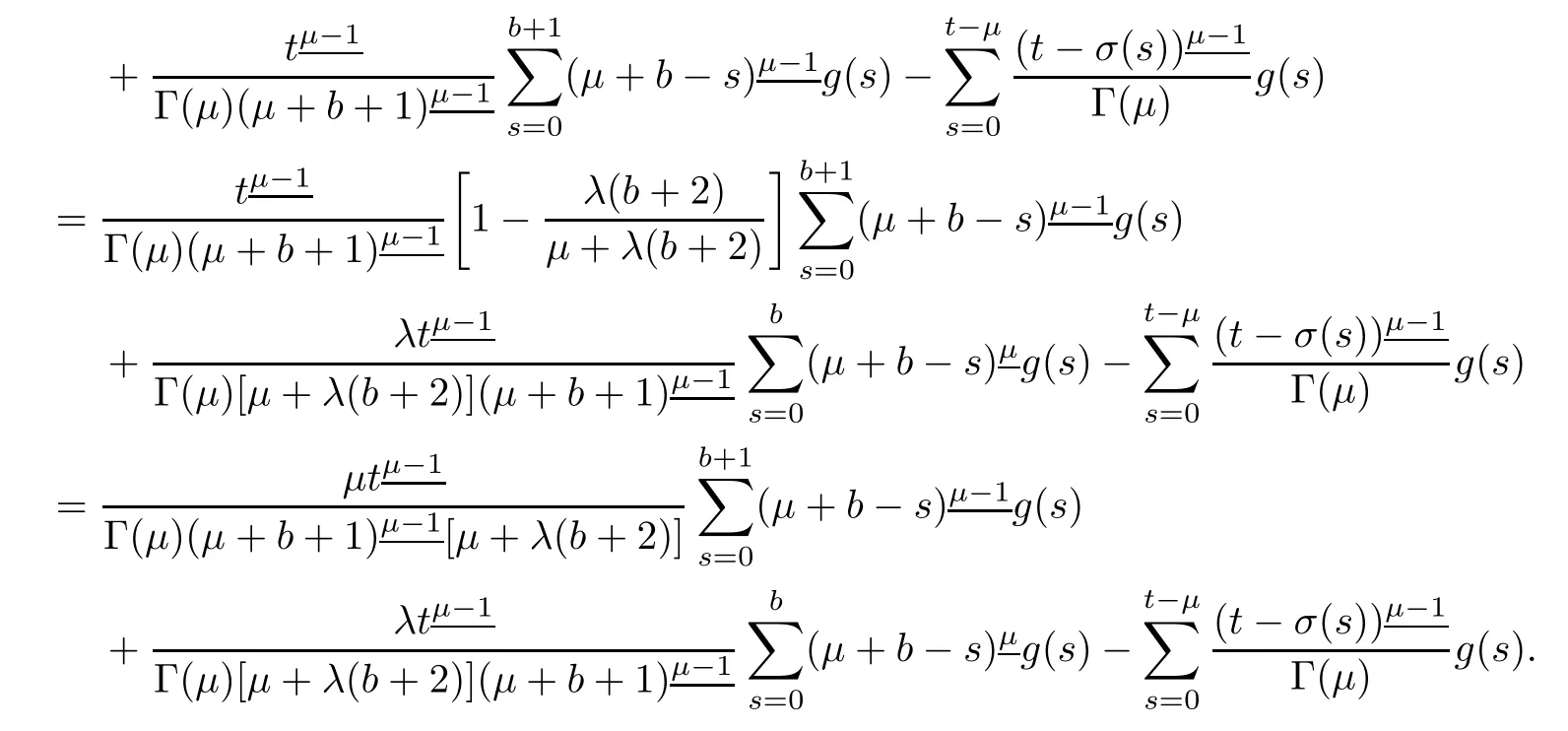
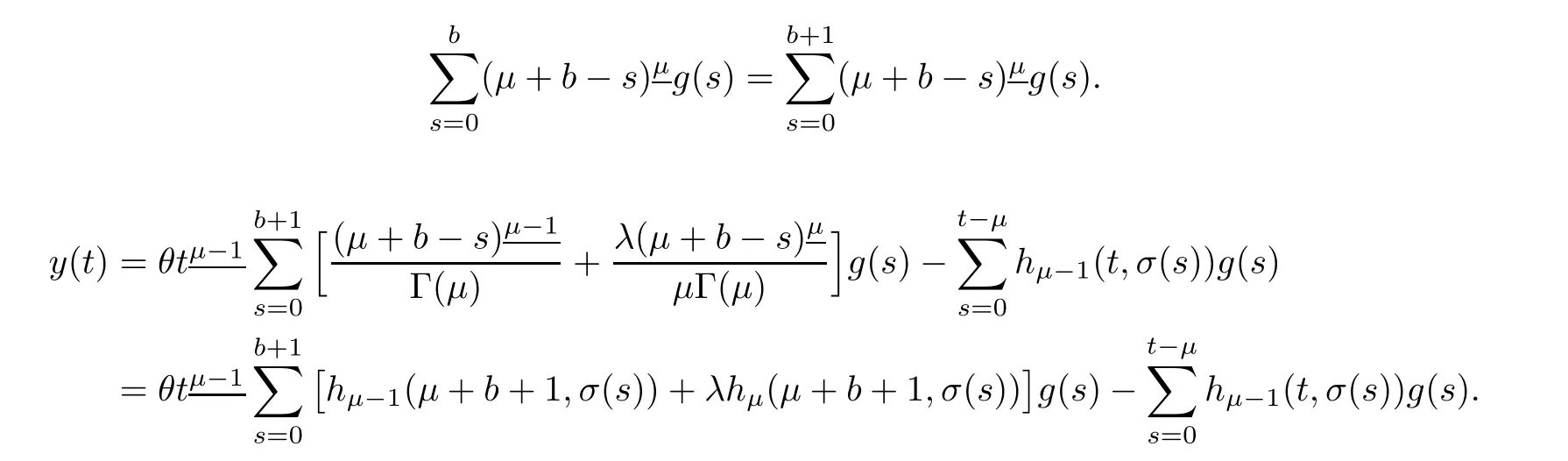
It follows that
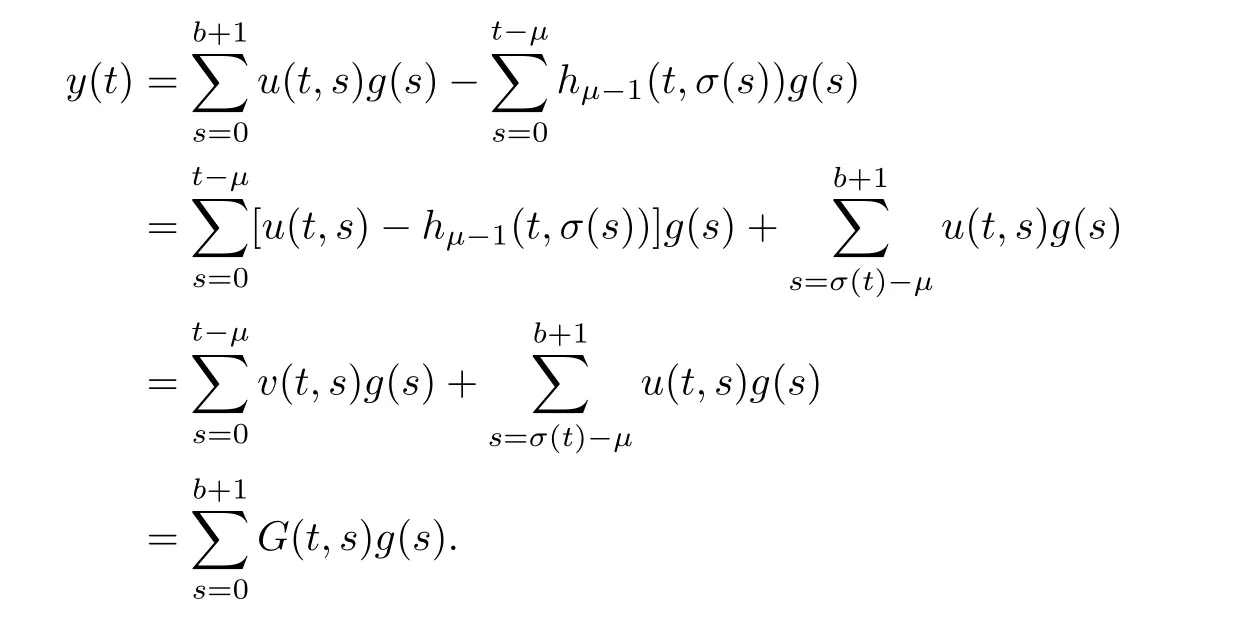
Hence,this completes the proof.
Next,we sum Green’s function onfor later use to prove the existence of solutions for nonlinear MPFBVP.
Lemma 3.2The Green’s function for MPFBVP(3.1)satisfies the identity
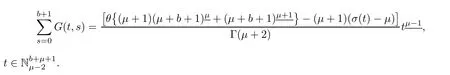
ProofForconsider the left hand side,then
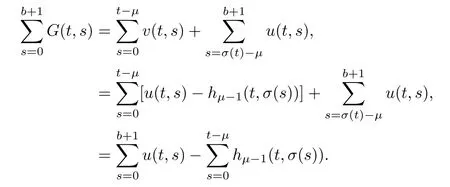

In the last step,we used the fact that
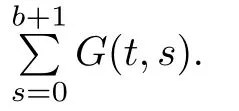
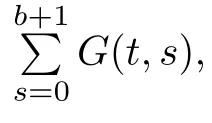
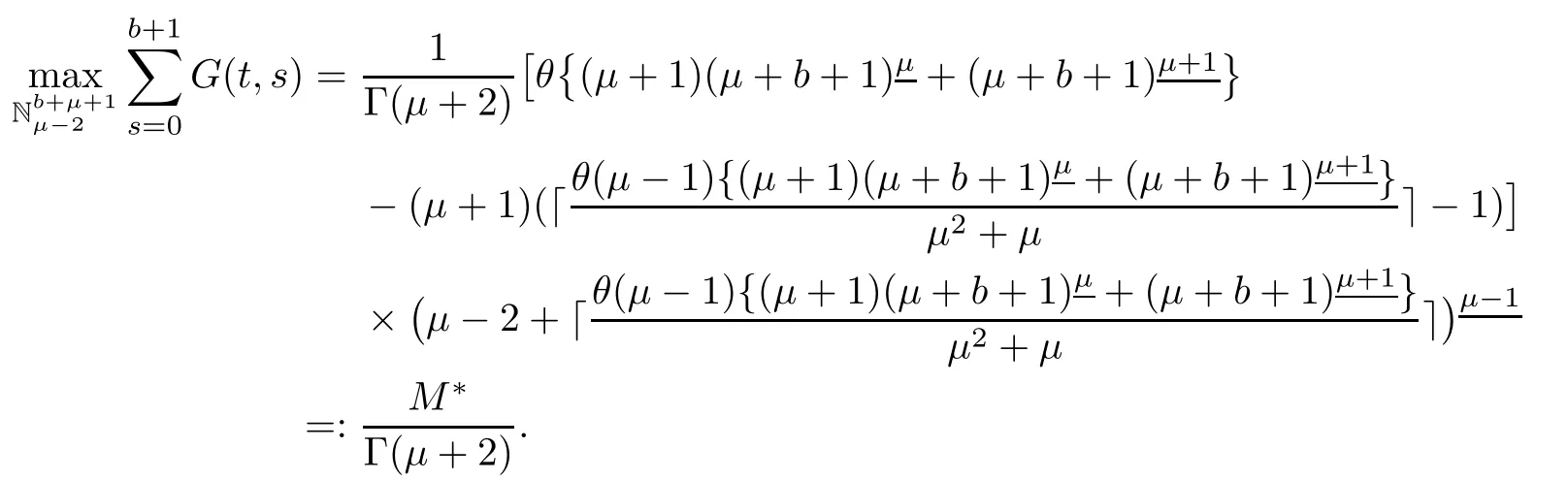
ProofBy Lemma 3.2,we have
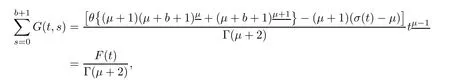
To find critical point of F(t),we consider
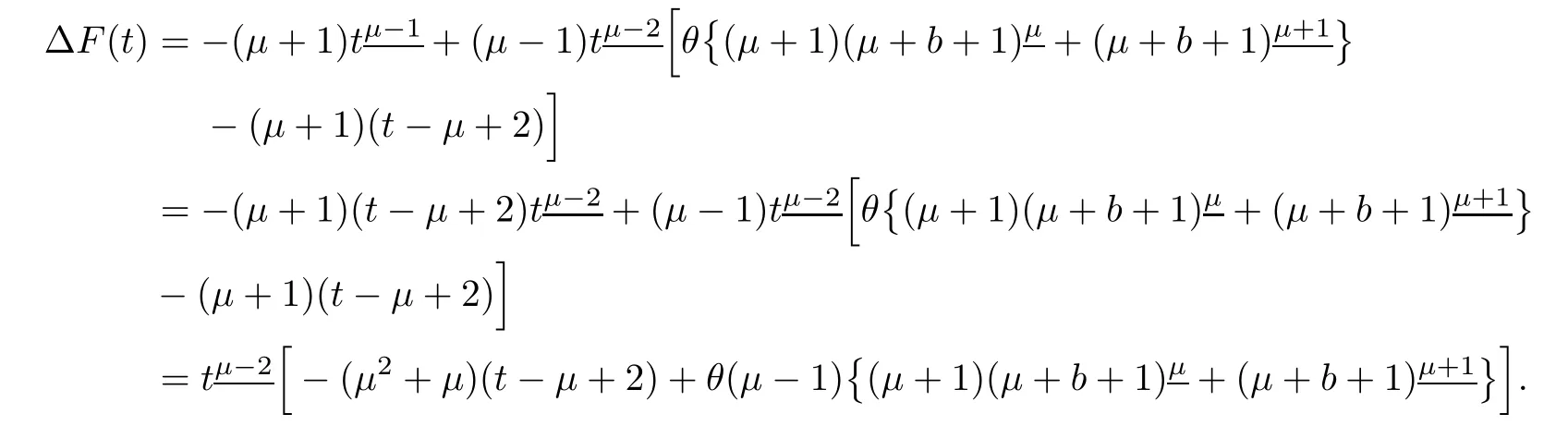
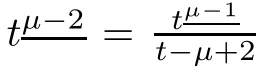
Theorem 3.4Assume thatμ∈(1,2],p,q∈R andThen,the solution to the non-homogeneous MPFBVP
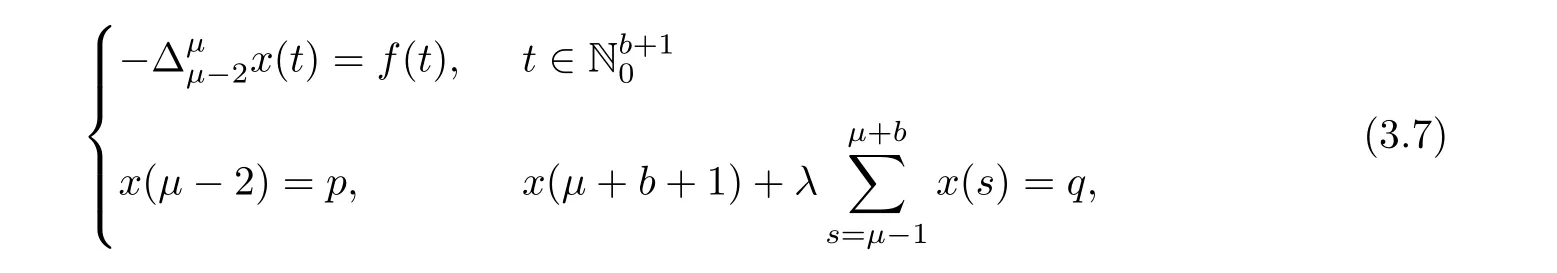
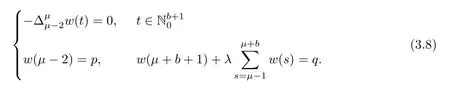
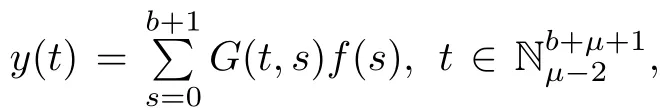
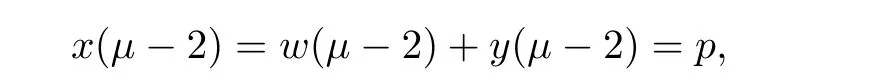
and
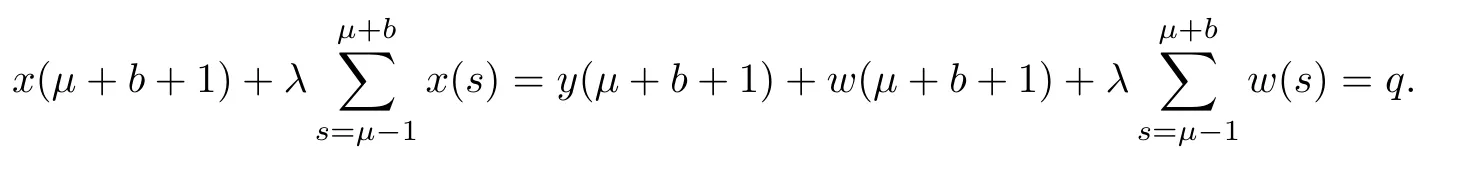
Finally,
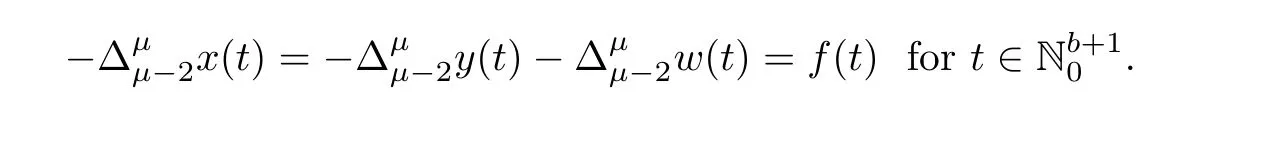
Theorem 3.4 can be helpful for treating nonlinear system with summation condition.The following result is an implication of Theorem 3.4.
Corollary 3.5Assume thatμ ∈ (1,2]andThen,the solution to system(1.1)is given by
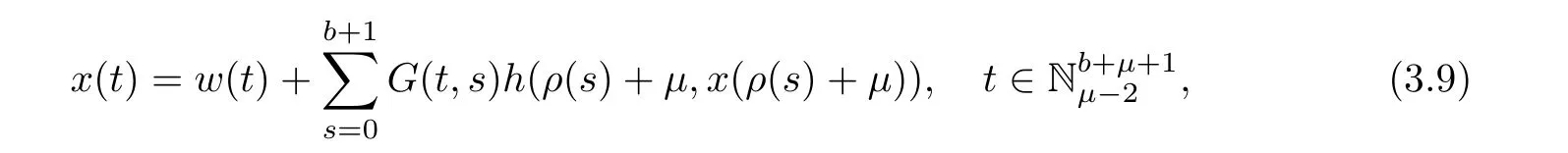
where w(t)is given in Theorem 3.4.
4 Existence and Uniqueness Conditions
The Schauder’s fixed Point theorem[45]is utilized for existence in the next theorem.
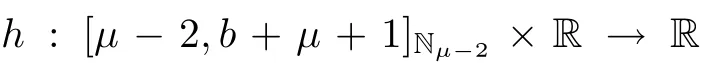
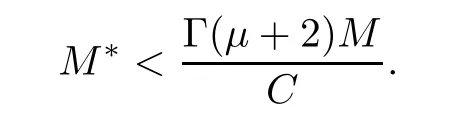
ProofDefine a normon space of real valued functions X by=max{|y(t)|:t∈so that the pairis a Banach space.Thus,X is a topological vector space.Define the compact,convex subsetof X.The operator T:X→X is given by
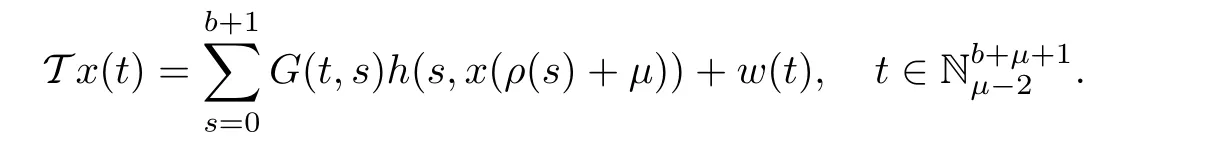
First,we shall show that T is self map.For arbitraryand x ∈ K,we have
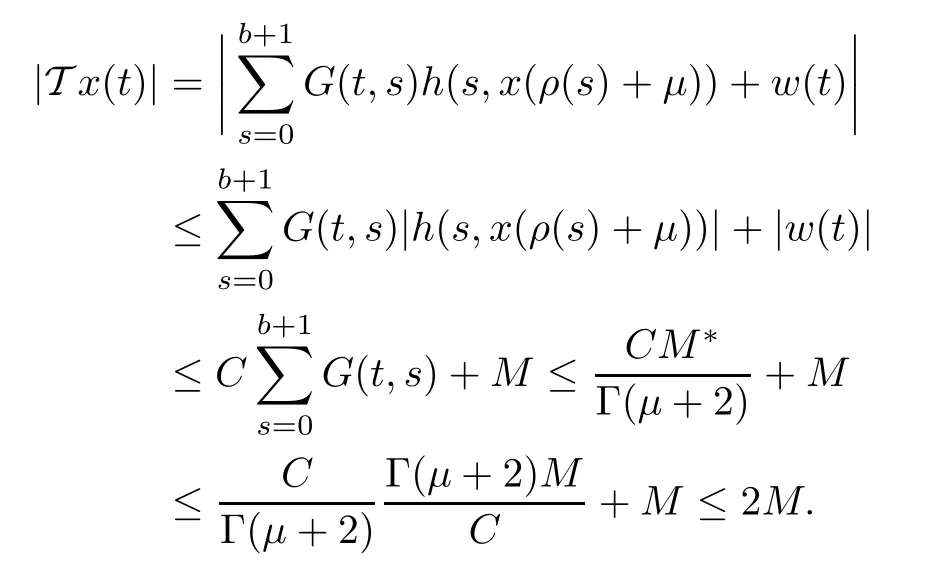
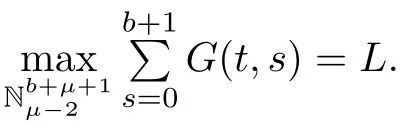
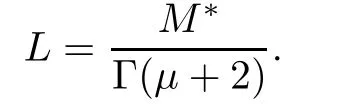
Continuity of h on R implies its uniform continuity on[?2M,2M].So,there exists δ>0 for all t,and for all x,we have
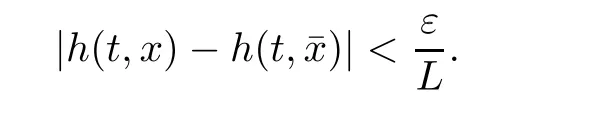
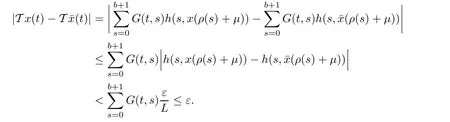
This proves the continuity of operator T from K into K.Thus,the application of Schauder’s theorem implies T(x)=x,for some x∈K.This prove the desired result.
The Contraction mapping theorem[45]is utilized for the uniqueness in the following theorem.
Theorem 4.2Assume thatis uniform Lipschitz in 2ndvariable,with constant k>0.Ifthen the nonlinear fractional boundary value problem(1.1)has unique solution.
ProofDefine a normon space of real valued functions X by=max{|y(t)|:t∈in such a way that(X,k·k)is a Banach space.Define operator T as stated in Theorem 4.1.To show that T is a contraction map,observe for alland for allthat
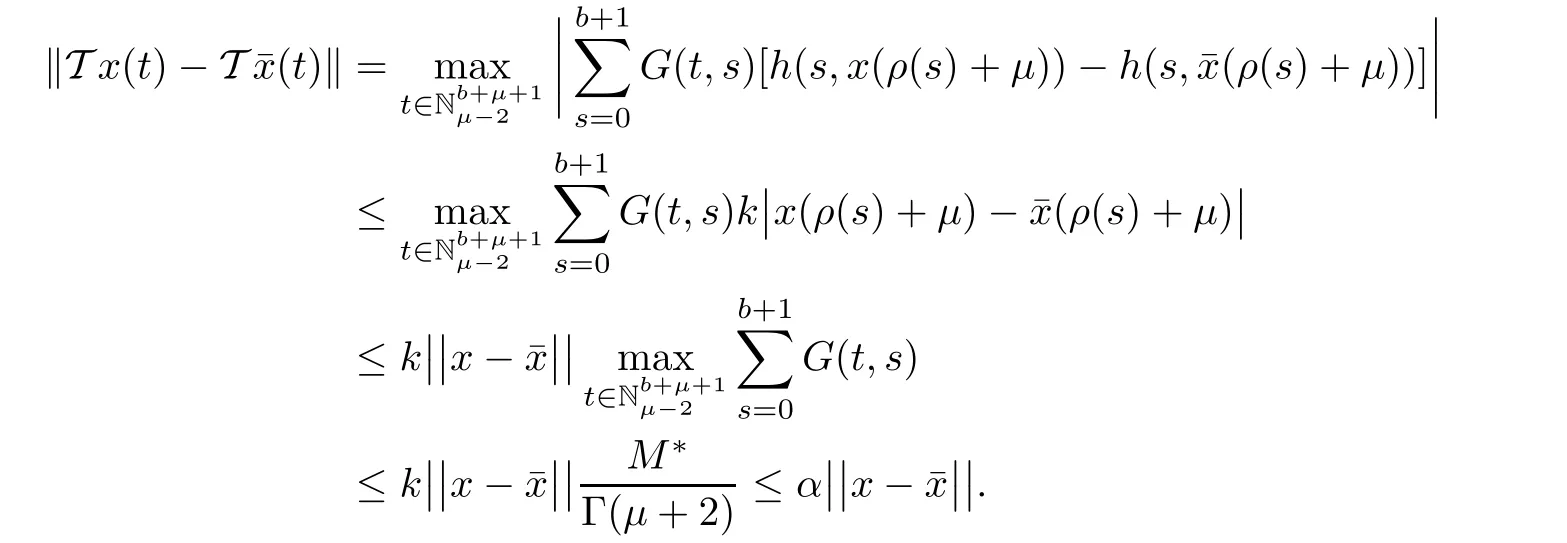
5 Conditions for Stability Analysis
ProofBy Corollary 3.5,the solution x(t)of nonlinear MPFBVP(1.1)is given by equation(3.9).From inequality(2.1),forit follows that

By making use of equation(3.9)and inequality(5.1)together for,we have
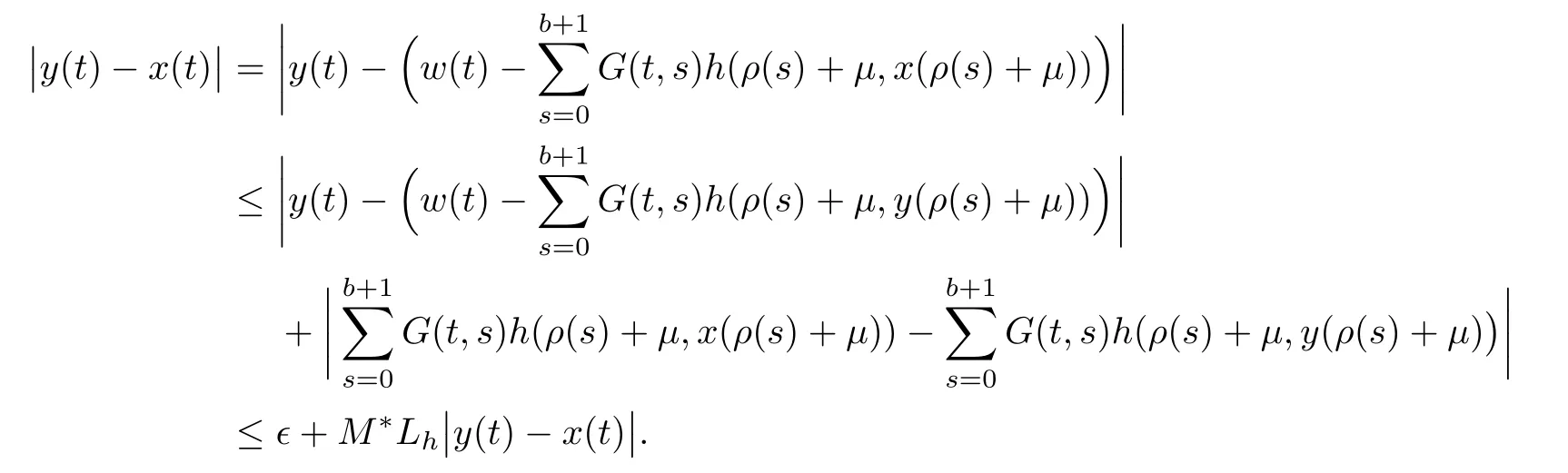
In preceding step,we use the assumption on h and Lemma 3.3.Simplification yields the following

Therefore,the solution of MPFBVP(1.1)is Ulam-Hyers stable.Further using φh(?)= ?dh,φh(0)=0 implies that the solution of system(1.1)is generalized Ulam-Hyers stable.
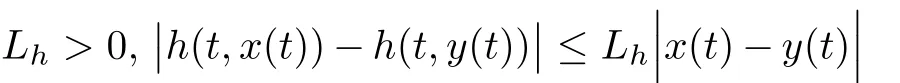
ProofBy Corollary 3.5,the solution x(t)of nonlinear MPFBVP(1.1)is given by equation(3.9).From inequality(2.2),for,it follows that
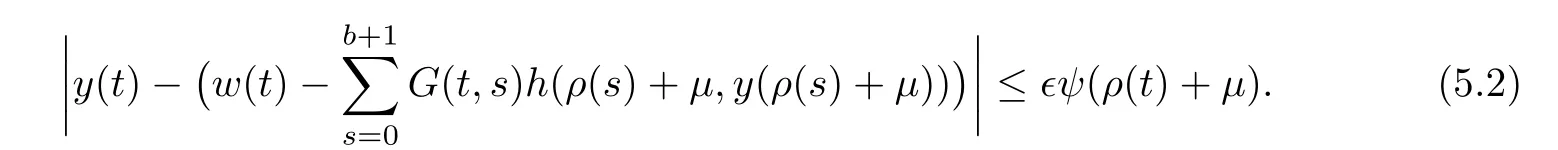
By making use of equation(3.9)and inequality(5.2)together for,we have
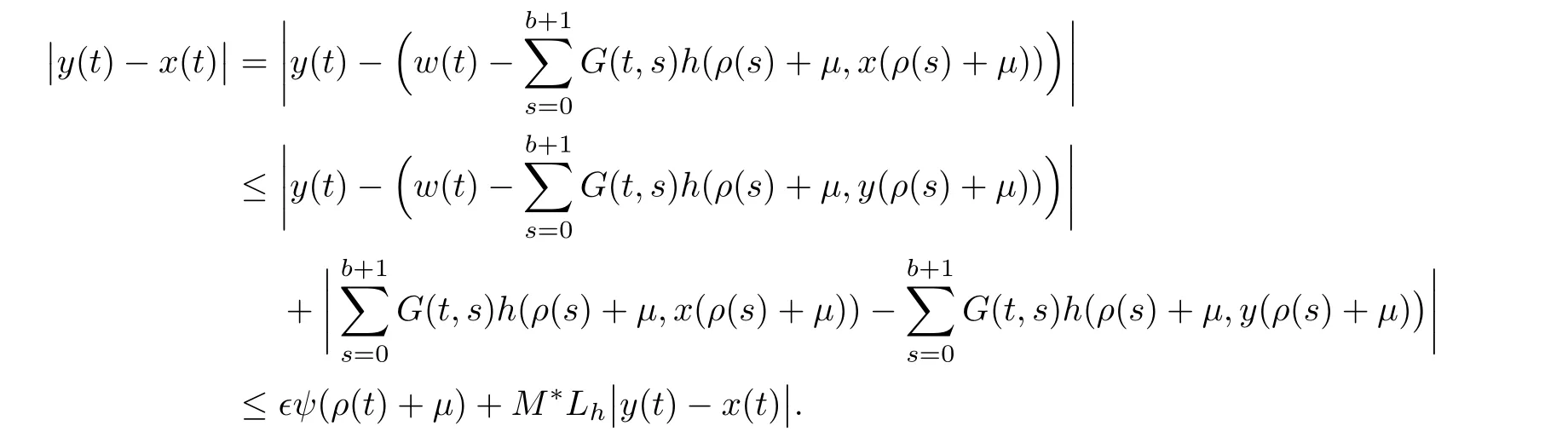
In preceding step,we use the assumption on h and Lemma 3.3.Simplification yields the following
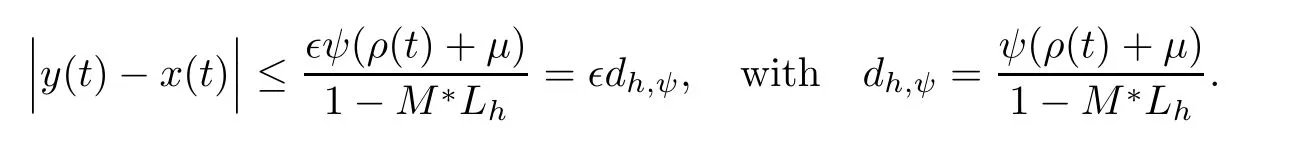
Therefore,the solution of MPFBVP(1.1)is Ulam-Hyers-Rassias stable.Furthermore,Φ(ρ(t)+μ)= ?ψ(ρ(t)+μ)implies that solution of system(1.1)is generalized Ulam-Hyers-Rassias stable.?Finally,to illustrate the usefulness of Theorem 5.1,we present the following example.
Example 5.3Consider the delta difference equation with summation condition
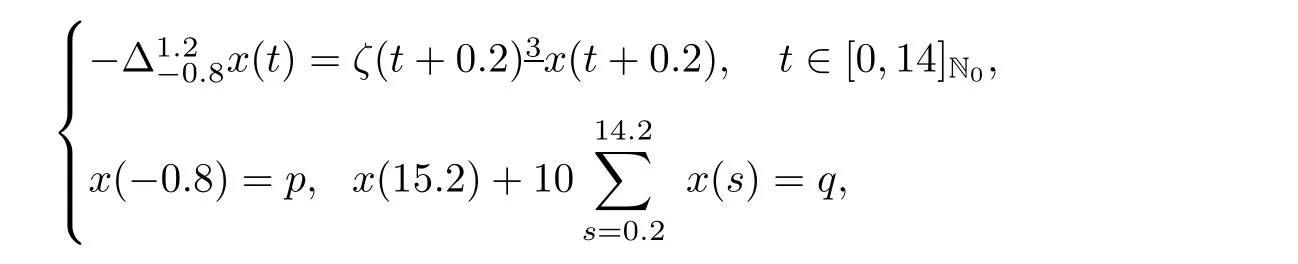
we have Lh=221.76ζ,foras b=13,μ =1.2,and λ =10,therefore M?=2.12.Then,forthe solution to the given problem with inequalities
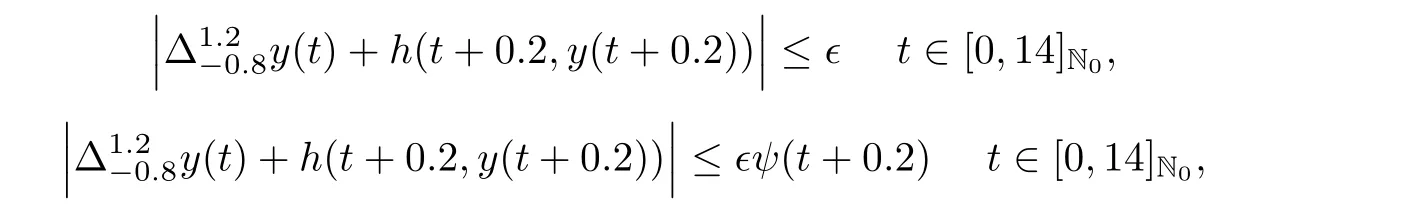
is,respectively,Ulam-Hyers stable and Ulam-Hyers-Rassias stable with respect to function
 Acta Mathematica Scientia(English Series)2020年2期
Acta Mathematica Scientia(English Series)2020年2期
- Acta Mathematica Scientia(English Series)的其它文章
- EXPANDABLE PARALLEL FINITE ELEMENT METHODS FOR LINEAR ELLIPTIC PROBLEMS?
- PROPERTIES ON MEROMORPHIC SOLUTIONS OF COMPOSITE FUNCTIONAL-DIFFERENTIAL EQUATIONS?
- MAXIMUM TEST FOR A SEQUENCE OF QUADRATIC FORM STATISTICS ABOUT SCORE TEST IN LOGISTIC REGRESSION MODEL?
- INITIAL BOUNDARY VALUE PROBLEM FOR THE 3D MAGNETIC-CURVATURE-DRIVEN RAYLEIGH-TAYLOR MODEL?
- STRONG INSTABILITY OF STANDING WAVES FOR A SYSTEM NLS WITH QUADRATIC INTERACTION?
- ON THE AREAS OF THE MINIMAL TRIANGLES IN VEECH SURFACES?
