Jaeuk Byun,Jong Won Shin

Electrical Engineering and Computer Science,Gwangju Institute of Science and Technology (GIST),Gwangju 61005,South Korea

Abstract: Nonnegative matrix factorization(NMF) has shown good performances on blind audio source separation (BASS).While the NMF analysis is a non-convex optimization problem when both the basis and encoding matrices need to be estimated simultaneously,the source separation step of the NMF-based BASS with a fixed basis matrix has been considered convex.However,because the basis matrix for the BASS is typically constructed by concatenating the basis matrices trained with individual source signals,the subspace spanned by the basis vectors for one source may overlap with that for other sources.In this paper,we have shown that the resulting encoding vector is not unique when the subspaces spanned by basis vectors for the sources overlap,which implies that the initialization of the encoding vector in the source separation stage is not trivial.Furthermore,we propose a novel method to initialize the encoding vector for the separation step based on the prior model of the encoding vector.Experimental results showed that the proposed method outperformed the uniform random initialization by 1.09 and 2.21dB in the source-to-distortion ratio,and 0.20 and 0.23 in PESQ scores for supervised and semi-supervised cases,respectively.

Keywords: blind audio source separation;nonnegative matrix factorization; speech enhancement

I.INTRODUCTION

NONNEGATIVE matrix factorization (NMF)is a technique to represent a nonnegative data matrix as a product of nonnegative basis and encoding matrices,which has gathered many interests in a wide variety of areas such as image and video signal processing,text mining and topic modeling,brain signal processing,and audio signal processing,etc [1]-[5].One of the prominent features of NMF is the nonnegativity constraint that makes NMF approximation results to be a part-based and highly interpretable representation of data.One of the most successful application of the NMF analysis is the blind audio source separation(BASS) [6],[7],which aims to recover the individual source signals from the mixture.The basic idea of NMF-based BASS is to represent the input magnitude or power spectra as linear combinations of sets of bases assuming that each set of bases can reconstruct corresponding source signals.The basis matrix for each source is trained separately using the corresponding signals.Trained basis matrices are concatenated to form the basis matrix for the source separation.

Many variations of the standard NMF analysis have been proposed with different divergence measures,optimization methods,and regularization terms.Popular divergence measures between the input and reconstructed matrices include Euclidean distance [8],generalized Kullback-Leibler divergence (or I-divergence) [8],Itakura-Saito divergence [9],and β-divergence [10],while multiplicative update rules (MuR) [8],projected-gradient method [11],and interior-point gradient method [12]are used for optimization.As for the regularization terms,sparsity constraints [13]-[15],discriminative constraints [16],[17],and prior model-based constraints [18]-[26]have been investigated.

This paper proposes the initialization of the encoding matrix for the source separation step.

There have been several researches on the initialization of the NMF [27]-[34].Most of them focused on the initialization of the basis matrix while a few approaches worked to initialize the encoding matrix,when both the basis and encoding matrices are jointly estimated as in the training phase of BASS.In contrast,the initialization of the encoding matrix with fixed basis matrix as in the source separation step of BASS hasn’t gotten much attention because the estimation of the encoding matrix given the data and basis matrices are considered to be a convex optimization and thus the initial point doesn’t matter.However,when the basis matrix is constructed by concatenating basis matrices that are individually trained for sources,it may not have a full column rank and the optimum encoding matrix may not be unique as is shown in Section III-A.Therefore,the initialization of the encoding matrix for the source separation step is not trivial even when the basis matrix is fixed,not to mention the semi-supervised NMF in which a part of basis matrix is adapted along with the encoding matrix.

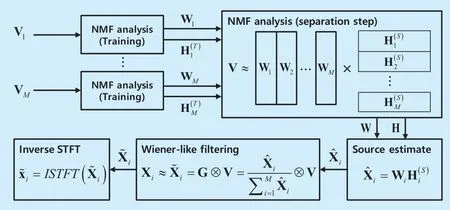
Fig.1.Overall block diagram of NMF-based BASS.

In most of NMF-based BASS researches,the encoding matrices from the training phase are discarded even though they have useful information about how each basis are utilized to reconstruct the source signals.To exploit this information,there have been many attempts to adopt prior models within Bayesian framework [22]or in forms of penalty terms [19]-[21]for which the parameters are estimated from the encoding matrix for the training data.However,prior models on the encoding matrix haven’t been used to initialize the encoding matrix for the source separation phase to the best of our knowledge.In this paper,we have shown that the source separation step with fixed basis matrix would have multiple optimal solutions,which makes the initialization of the encoding matrix valuable.Also,we propose an initialization method based on prior models for which the parameters are estimated from the encoding matrix for the training data.We have compared the proposed prior model-based initialization method with the existing encoding vector initialization methods for three NMF-based BASS systems including the standard NMF [8],the NMF with the exponential model-based penalty term [20],and the sparse NMF (SNMF) [14].Experimental results showed that the proposed method outperformed conventional methods not only for the semi-supervised NMFs,but also supervised NMFs.

II.NMF-BASED AUDIO SOURCE SEPARATION

NMF basically decomposes the nonnegative data matrix V∈?FN×into the nonnegative basis matrix W∈?FK×and the nonnegative encoding matrix H∈?KN×to find the best approximation VWH≈.It can be formulated as an optimization problem as follow:

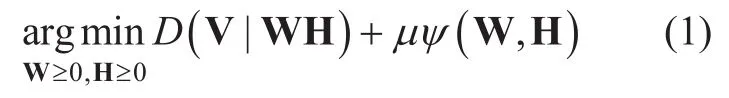
whereD(a|b) is a measure of how differentaandbare,A≥0 denote element-wise nonnegativity of a matrix A,andψ(W,H)is a task-specific regularization term with weight ofμ.Popular choices forD(a|b)includes the Euclidean distance,the generalized Kullback-Leibler divergence (KLD),and the Itakura-Saito divergence,which are special cases of the beta divergence.The basic form of the MuR without the regularization term when KLD is used,i.e.,,is given as

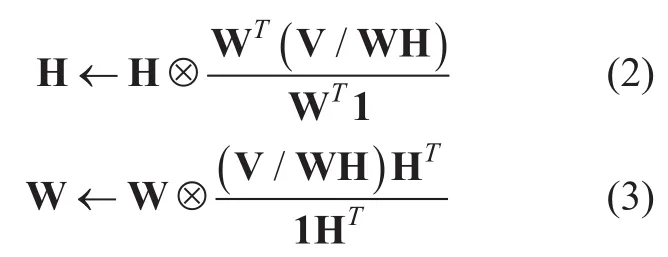
In the NMF-based BASS,the magnitude or power spectrogram is used as a non-negative data matrix V∈?F×NwhereFis the number of frequency bins and N is the number of frames.The process of the NMF-based BASS is shown in figrue 1,which consists of the training and source separation steps followed by a filtering similar to Wiener filter.In the training step,the basis matrix Wi∈?F×Kifor each sourceiis obtained separately by the NMF analysis of the corresponding source signalwhereKiis the number of basis vectors corresponding to the sourcei,andis the number of frames in the training data for sourcei.

In the separation step of basic supervised NMF-based BASS,NMF analysis is applied to the input mixture magnitude or power spectrogram V(S)∈?F×N(S)with a fixed basis matrixwhich is the concatenation of the basis matrices trained for each source,whereN(S)is the number of frames in the test data andK=∑iKiis the total number of bases.Because only the encoding matrix is updated,(2) is iteratively applied for a fixed number of times or until a certain stopping criterion is met.As for the semi-supervised NMF,there are extra bases Wein addition to the trained bases which are updated during the source separation procedure along with the encoding matrix.The extra bases are adapted to the current input components that cannot be reconstructed by trained bases well,which makes the source separation performance robust when there exist signals unseen during the training.The update rule is the same as (2) and (3) except that only a part of the basis matrix is updated.In fact,the supervised NMF can be viewed as a special case of the semi-supervised NMF with zero extra bases.Once we have obtained Weand the encoding matrixeach source signal is approximated as

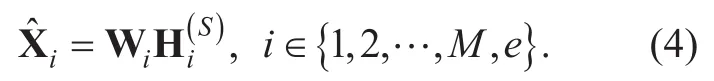
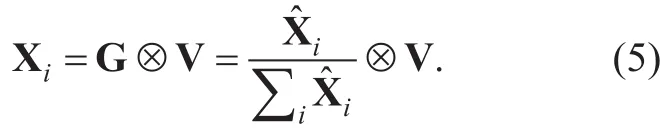
Then,the separated source signal can be obtained through the inverse short-time Fourier transform (STFT) and overlap-add method.

In [20],an NMF-based BASS based on a prior model for the encoding vector is proposed.In this approach,the regularization termψ(W,H) for the source separation step is the negative log likelihood of the encoding matrix H where the distribution of each encoding vector h is modeled as an independent exponential distribution for which the parameters are obtained from the encoding matrix for the training data.If the distribution of h is modeled asis given asand the MuR with KLD becomes

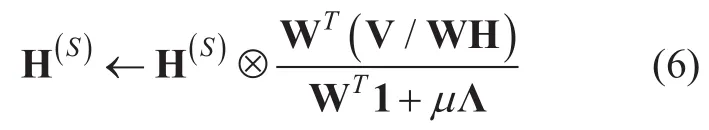
Another notable modification of the standard NMF described above is the sparse NMF[14],which dramatically enhances the performance of BASS.SNMF uses the regularization termto enforce sparse encoding matrix,while the column-wise normalized version of W,replaces W in the objective function.The objective function of SNMF is given as

The MuR for the SNMF with KLD becomes

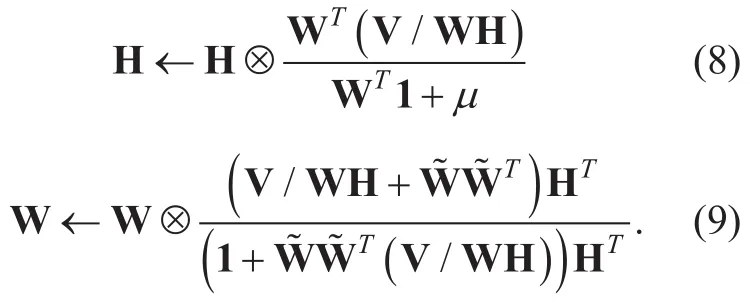
III.INITIALIZATION FOR NMF-BASED BASS PROBLEM

3.1 Non-uniqueness of separation step

It is well known that NMF is a non-convex optimization problem when W and H are jointly estimated,which is the case for the training phase of the NMF-based BASS.However,the source separation step of the supervised NMF-based BASS that only estimates H given V and W is considered to be convex,and therefore the initialization of H in this step has been gathered few attention.Since,however,W is constructed by concatenating basis matrices for the sources trained separately,Wi’s,the rank of W can be less thanKand then the encoding vector that minimizes the cost function may not be unique.

Letcabdenote the (a,b)-th element of matrix C.When the subspaces spanned by basis vectors for the sources overlap,the concatenated basis matrix W is not of a full column-rank,which implies that there exists at least one linearly dependent basis vectorThen,we have

by lettingπl(wèi)=-1.Suppose that H is the encoding matrix that minimizes the divergence between V and WH,D(V| W H).The divergence can be represented as

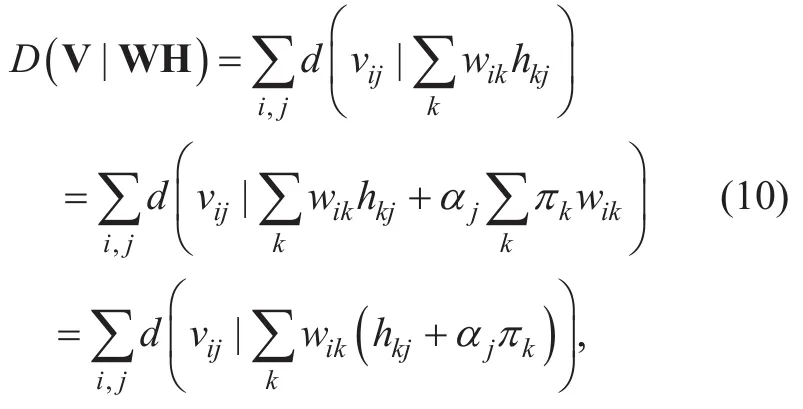
for any constantsαj's.Therefore,if we letG becomes another encoding matrix that results in the same divergence as H for all values ofαjfor whichgkj≥ 0 for allk.Thus,the optimum solution for H that minimizes the divergence between V and WH is not unique in general,which makes the initialization of H in the source separation phase nontrivial even when the number of iterations is high enough.

3.2 Initialization using prior knowledge on encoding vectors

Unlike the basis initialization method for the training phase [27]-[34],only a few methods have been proposed to initialize the encoding matrix for the source separation phase including uniform random initialization [8]and initialization of H as WTV [35].Both of the approaches have provided decent results,but lack rigorous mathematical background.

The encoding matrices from the training phase,contain important information about how each basis was encoded.However,most of NMF-based BASS algorithms discard them but use only the trained basis vectors.There have been several researches to utilize prior models for the encoding vectors either in the form of a penalty term [19]-[21],or within Bayesian framework [18],[22]-[26].Some of them estimate parameters of the prior models from[19]-[22],while others used fixed parameters that maximized the performances.Although these approaches utilize the information into modify the cost function,the H in the separation phase was still initialized as uniform random numbers.

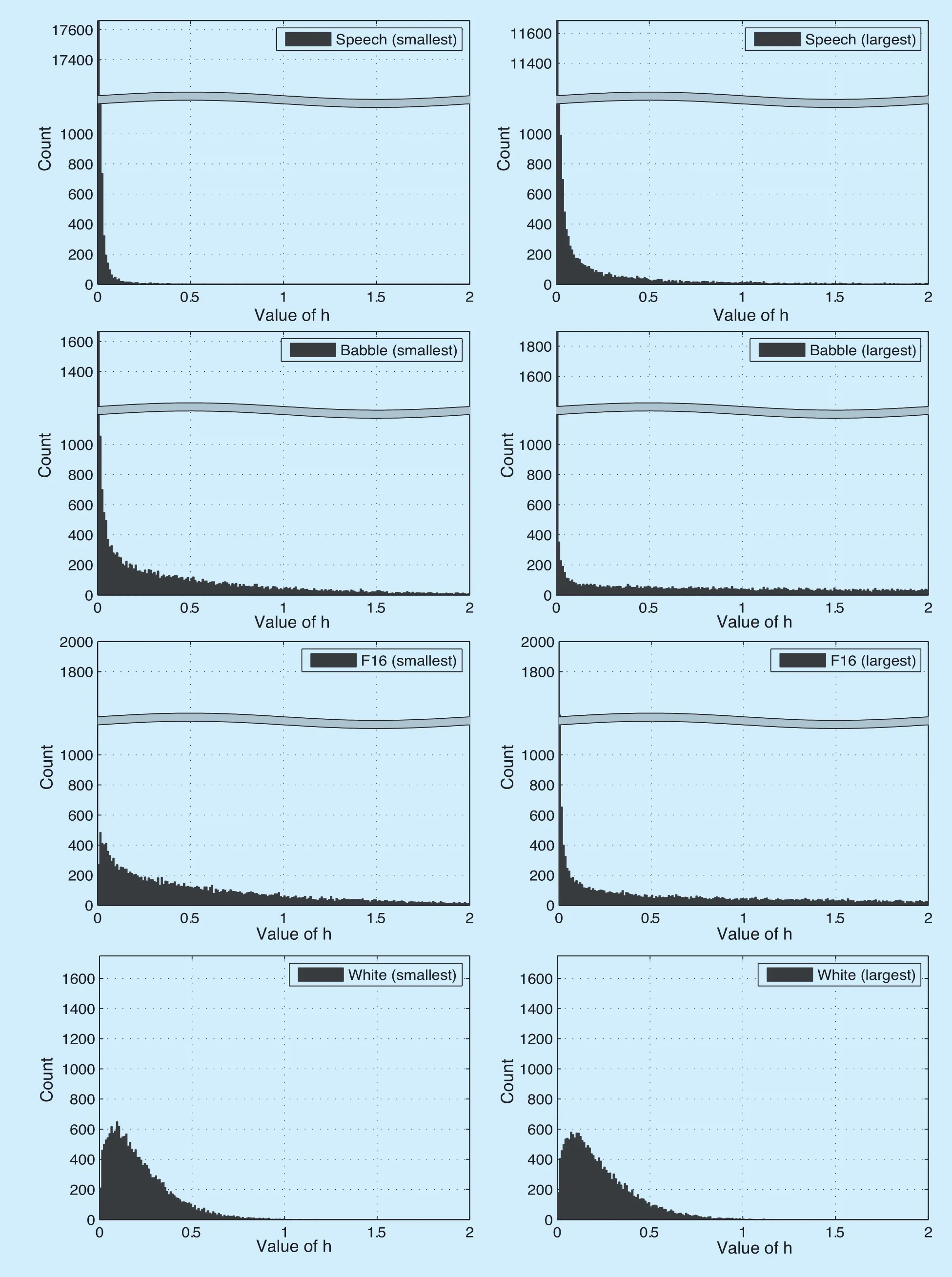
Fig.2.The histograms of encoding coefficients for the most rarely (left column) and frequently (right column) used basis vectors for speech,babble,f16,and white noises.

In this paper,we propose the initialization of the encoding matrix for the source separation step based on prior models for H obtained fromTo select a suitable statistical model for H,we first analyzed the empirical distribution of the encoding vectors at the training step.We have obtained the encoding matrices for several source signals by the standard NMF analysis with KLD as a divergence measure and MuR as an optimization method.The signals were speech utterances in TIMIT database [36]and babble,F-16 and white noises from NOISEX-92 database [37],which were resampled at 16kHz.512-point FFT was applied with 75% overlap to form the spectrogram.Fandwere set to 257 and 212989,respectively,while the number of bases were 128 for speech and 26 for other signals.Figure 2 shows the histograms of the encoding vector elements that have the smallest and largestl1-norms,which roughly correspond to the most rarely and frequently used bases,respectively.It is clear that the distributions of components of H were far from the uniform distribution.The distributions were closer to the Rayleigh distribution for white noise and the exponential or gamma distribution for other signals.We can also see that the distribution for each component of H is quite different from each other.In this paper,we model the distributions for the components of H as independent exponential distributions with distinct parameters as in [18],[20],[22].The probability density function (PDF) is given by

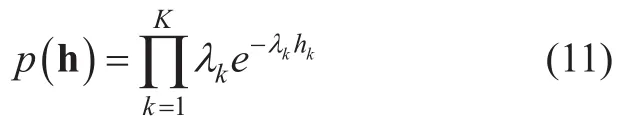
where h is an encoding vector,hkis a component of h corresponding to thek-th basis vector,andλkis the reciprocal of the mean ofhkestimated fromRandom samples following the PDF in (11) are generated to initialize H for source separation step using the MATLAB function ''exprnd'' in the statistics toolbox.As the power level of the test signals can differ from that of the training data,the initial encoding vector for then-th frame,is further modified so that then-th data vector vnand the reconstructed onehas the same power:

IV.EXPERIMENTS AND RESULTS

To evaluate the performance of the proposed initialization method,it is applied to NMF-based source separation in which the target signal is speech.The divergence measure and the optimization method were KLD and MuR,respectively.The standard NMF [8],the NMF with a penalty term based on the prior model for encoding vector in [20](ExpNMF),and the SNMF with normalized bases in the objective function [14]were employed with the conventional uniform-random method [8],the initialization by WTV [35]and our proposed prior model-based initialization method.Both supervised and semi-supervised NMFs introduced in Section II were tested.The performance of the source separation is measured in terms of the source-to-distortion ratio(SDR) [38]and the ITU-T Recommendation P.862 perceptual evaluation of speech quality(PESQ) score [39].

The training and test DB were composed of the speech samples from TIMIT dataset[36]and 6 types (babble,f16,factory2,machinegun,white,leopard) of noise samples from NOISEX-92 dataset [37].All datasets are sampled at 16kHz,and the input spectrogram is obtained using 512-point discrete Fourier transform with 75% overlapped Hamming windows.For the training,175 seconds of speech spoken by 29 male and 29 female speakers and 180 seconds long noise signals for each type were used.As for the test,16 sentences from 16 speakers mixed with 6 types of noises at -5,0,and 5dB signal-tonoise ratios (SNRs) were utilized.There were no overlap between signals or speakers used in training and test.For the supervised NMF,128 basis vectors trained for speech signal and 21 bases trained with each type of noise were concatenated to form the basis matrix with 254 bases.The numbers of bases were chosen to provide a good compromise between performance and computational cost while keeping a balance between the target signal and interferences.As for the semi-supervised NMF,128 speech bases and 128 extra basis vectors were appended to form the basis matrix of 256 columns without trained interference bases.The extra bases were initialized with uniform random numbers and updated in the source separation step according to MuR.The encoding matrix components corresponding to the extra bases were initialized with uniform random numbers for all compared systems because there are no prior information for them.The number of iterations for the training stage was 50.The number of iterations in the separation step and the weight for the sparsity termμwere set to maximize the source separation performance for each method,which fell into the range of [0,384]for the number of iteration and [0.5,5]forμ,respectively.

The performances were averaged over 10 trials with different random seeds.Table I and Table II show the SDR and PESQ results when the input SNRs were +5dB,0dB,and-5dB,respectively.The speech level of the test data was kept the same as the training speech level,while the noise levels were adjusted to result in the required SNRs.As seen in the tables,the proposed initialization method outperformed other initialization methods in terms of both SDRs and PESQ scores for all NMF-based BASS methods and all SNRsexcept the supervised standard NMF at +5dB SNR.In virtue of the power normalization in the equation (12),the mismatch between training and test data levels didn’t degrade the performances.The performances were also improved for the supervised NMFs which were traditionally considered as convex optimization problems,which verified our analysis on the non-uniqueness of the NMF solutions in the source separation step in Section III.A.As for the semi-supervised NMF which updates the encoding matrix along with a part of the basis matrix,initialization of H showed more inf l uence on the performance as expected.On average,the proposed initialization improved the better of the two conventional initialization methods by 0.43 and 2.21dBs of SDRs and 0.20 and 0.23 of PESQ scores for supervised and semi-supervised NMFs,respectively,for the standard NMF.The performance improve-ments for SNMF were as small as 0.07 and 0.63dBs in SDRs and 0.07 and 0.10 in PESQ scores,but the p-values were lower than 0.001.

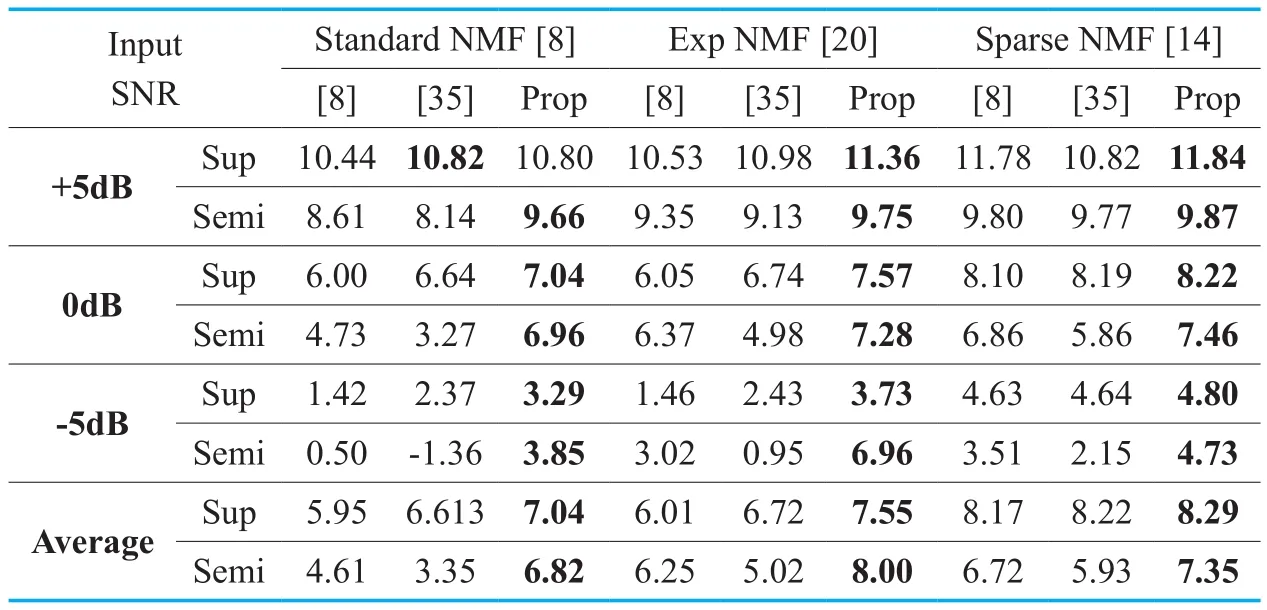
Table I.The source-to-distortion ratios (SDRs) for various initialization methods for each SNR averaged over 6 types of noises.

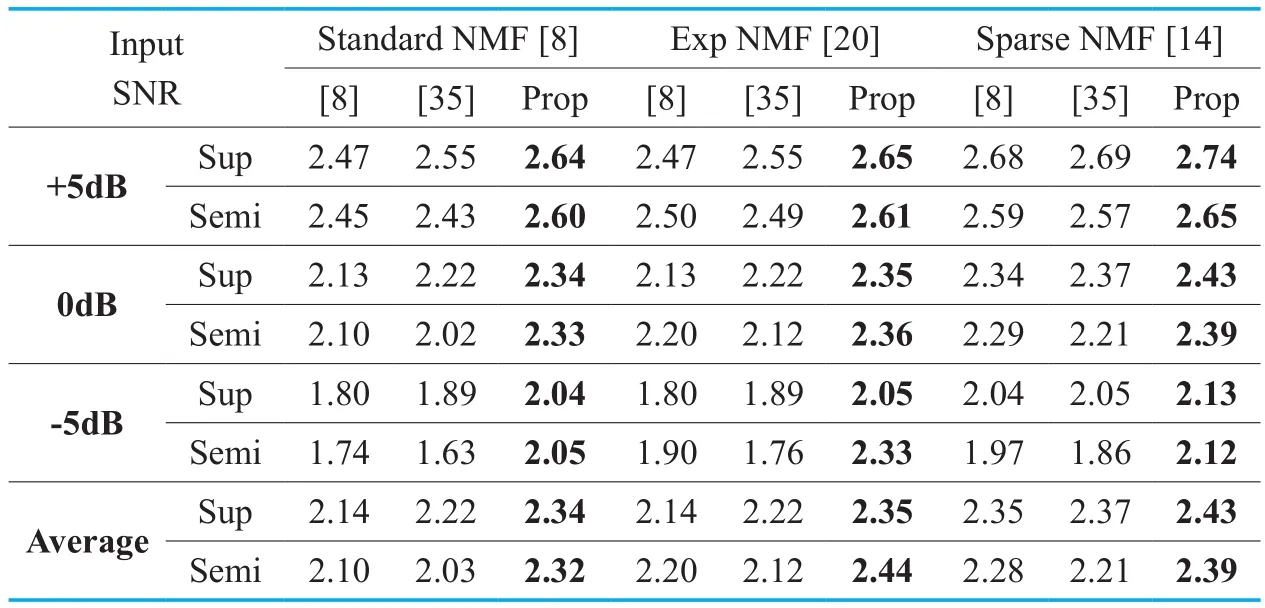
Table II.The PESQ scores for various initialization methods for each SNR averaged over 6 types of noises.

To illustrate the performances depending on the types of noises,we have shown the SDRs of the uniform random and proposed initialization methods for the standard and sparse NMFs at 0dB SNR for each type of noise in figure 3.The biggest improvement was for the machinegun noise with semi-supervised NMF.The machinegun noise has many time frames without any noise in which the extra bases for the semi-supervised NMF may adapt to the desired signal component that cannot be represented by Wsand the initial encoding matrix H(0).With proper initialization,the adaptation of Wein the noiseless period may be limited from the early stages of iterations,which could be the possible reason for this big improvement.

V.CONCLUSION

This paper proposes the initialization of the encoding matrix for the source separation step.It is shown that even when the basis matrix is fixed,the optimum encoding matrix may not be unique when the basis matrix is constructed by concatenating basis matrices for the sources.We have proposed to initialize the encoding matrix by random numbers following the prior model for which the parameters are estimated from the encoding matrix for the training data,which in turn are scaled to match the input power.Experimental results showed that the proposed method outperformed uniform-random initialization for both supervised and semi-supervised NMFs.

ACKNOWLEDGEMENT

This work was supported by the research fund of Signal Intelligence Research Center supervised by the Defense Acquisition Program Administration and Agency for Defense Development of Korea.