系統(tǒng)H∞范數(shù)計算:Lyapunov函數(shù)的直接優(yōu)化方法
劉秀翀 王占山
H∞控制理論主要研究抑制干擾和不確定性問題[1].在H∞控制理論中,傳遞函數(shù)(或系統(tǒng))的H∞范數(shù)是一項重要的性能指標,用于度量擾動輸入對系統(tǒng)輸出的影響,反映了閉環(huán)系統(tǒng)的抗擾能力.在H∞控制理論研究中,長期存在一個挑戰(zhàn)性議題:是否能夠直接給出關于H∞范數(shù)的通用解析表達式,進而避免針對線性矩陣不等式(Linear matrix inequality,LMI)約束條件的繁瑣的H∞范數(shù)近似尋優(yōu)方案.
在20 世紀80 年代,H∞控制理論的研究由頻域轉換到時域,開啟了基于狀態(tài)空間方程描述的系統(tǒng)魯棒性能研究[2].總的來說,H∞性能時域分析面臨的核心問題是如何選擇適當?shù)睦钛牌罩Z夫函數(shù).具體表現(xiàn)為基于李雅普諾夫方程[3?4]或參數(shù)化Riccati 不等式[5]均難以得到用于精確分析系統(tǒng)H∞性能的最優(yōu)李雅普諾夫函數(shù),因此在早期的研究中結果的保守性是難以避免的.
為精確求解H∞范數(shù),有學者提出了有界實引理[6],并將求解H∞范數(shù)問題轉化為時域狀態(tài)空間的約束優(yōu)化問題.基于有界實引理給出的LMI 約束條件,H∞范數(shù)能夠被近似尋優(yōu)[7?14].在LMI 方法中,H∞范數(shù)的尋優(yōu)一般包含以下步驟:
1)給出一個充分大的初始H∞范數(shù)估計γ;
2)解LMI 問題;
3)遞減H∞范數(shù)估計γ,直到獲得滿足LMI 條件的最小H∞范數(shù)估計γ.
顯然,一旦最小H∞范數(shù)估計得到,則通過解LMI,可以得到相應的近似最優(yōu)李雅普諾夫函數(shù).不難發(fā)現(xiàn),LMI 方法存在一定不足,表現(xiàn)為:
1)對于每一個給定的γ,LMI 條件需要被重復求解,直到找到最小的H∞范數(shù)估計,過程過于繁瑣;
2)這種試湊逼近方法無法揭示系統(tǒng)結構和參數(shù)對H∞性能的影響,在一定程度上限制了控制器精細設計的研究.
為了克服目前關于H∞范數(shù)問題研究的不足,一個可替換的方法是直接優(yōu)化李雅普諾夫函數(shù),進而得到關于H∞范數(shù)的通用解析表達式.目前,針對系統(tǒng)具體性能,難以找到李雅普諾夫函數(shù)設計的充要條件,因此這方面的研究并不多見.事實上,在分析系統(tǒng)具體性能時,存在最優(yōu)的李雅普諾夫函數(shù),并且這一最優(yōu)李雅普諾夫函數(shù)與系統(tǒng)結構和參數(shù)存在內(nèi)在關系[15].因此本文嘗試尋找一種李雅普諾夫函數(shù)的直接優(yōu)化途徑,進而實現(xiàn)H∞性能的精確分析.
由于多數(shù)高階系統(tǒng)在一定的條件下可以近似(或分解)為二階系統(tǒng)來研究,并且二階系統(tǒng)的分析方法是分析高階系統(tǒng)的基礎[16],因此為有效展現(xiàn)最優(yōu)李雅普諾夫函數(shù)與系統(tǒng)結構和參數(shù)存在內(nèi)在關系,本文針對一類二階系統(tǒng)的H∞范數(shù)問題,構造和優(yōu)化李雅普諾夫函數(shù),進而得到H∞范數(shù)的通用解析表達式.本文的研究避免了LMI 方法中繁瑣的近似尋優(yōu)過程,并展示了系統(tǒng)矩陣特征值的實部和虛部對H∞性能的影響.本文結構如下:第1 節(jié)分析H∞范數(shù)問題;第2 節(jié)分析Riccati 不等式中李雅普諾夫函數(shù)的選擇對求解H∞范數(shù)的影響;第3 節(jié)展現(xiàn)李雅普諾夫函數(shù)的直接優(yōu)化方法,并給出H∞范數(shù)的通用解析表達式;第4 節(jié)給出算例,驗證李雅普諾夫函數(shù)直接優(yōu)化方法的有效性.
1 問題的提出
1.1 問題描述
系統(tǒng)描述為

其中,x ∈R2,A為Hurwitz 矩陣,A的特征值為復數(shù),w為擾動輸入,≤δ,δ為常數(shù),
研究的問題是如何得到系統(tǒng)(1)的狀態(tài)上界.在數(shù)學意義上,這一問題可轉化為關于輸入–輸出系統(tǒng)的H∞范數(shù)問題,其中系統(tǒng)描述為

在H∞控制理論中,系統(tǒng)的H∞范數(shù)定義為S右半平面上解析的有理函數(shù)陣的最大奇異值.在標量函數(shù)中就是幅頻特性的極大值,代表了系統(tǒng)對峰值有界信號的傳遞特性.
1.2 LMI 方法分析
令李雅普諾夫函數(shù)為V=xTPx,γ為系統(tǒng)(2)的H∞范數(shù),即γ=∥G∥∞,其中G(s)=(sI ?A)?1為系統(tǒng)(2)的傳遞函數(shù).根據(jù)有界實引理,可得

LMI 方法是尋找式(3)中γ的最小值γmin.由于李雅普諾夫函數(shù)V=xTPx可以任意構造,因此對于每一個給定的γ,需要重復求解LMI,以判斷式(3)的存在性,直到γmin被找到.顯然,在LMI 方法中復雜的優(yōu)化過程是不可避免的.事實上,γmin與最優(yōu)的P矩陣是一一對應的.如果能夠直接給出最優(yōu)的P矩陣,則γmin的表達式就能夠得到,進而避免LMI 方法中復雜的優(yōu)化過程.本文的工作是嘗試提供一種新的途徑來直接給出γmin的表達式.
2 H∞范數(shù)分析
根據(jù)特征值和奇異值分解原理,可以得到下面的特性.
特性1.對于系統(tǒng)(2)中特征矩陣A,存在可逆矩陣T,滿足

其中,T=ΘT1×diag{t1,t2}×ΘT2,ΘT1和ΘT2為正交矩陣,t2≥t1>0,λ >0,ν >0.diag{t1,t2}表示對角元素為t1,t2的對角陣.
令α=t2/t1≥1,y=ΘT2×x,?=ΘT2×w.由式(2)和特性1,得
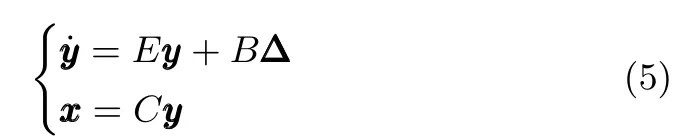
其中,B=I為單位陣,并且系統(tǒng)(2)和(5)具有相同的H∞范數(shù).
根據(jù)文獻[5]中引理2.1,可以得到下面的特性.
特性2.對于系統(tǒng)(5),存在正定矩陣X,滿足Riccati 不等式

其中,γ <ρ,γ=∥G∥∞為系統(tǒng)H∞范數(shù),ε為趨于零的正數(shù).
注1.應用Riccati 不等式一般會得到具有很強保守性的結果,但這種保守性并不是Riccati 不等式本身導致的.研究表明:基于李雅普諾夫函數(shù)的準確選擇,可以將特性2 中Riccati 不等式轉化為等式,進而精確給出H∞范數(shù).因此,導致這種保守性的原因是:在應用Riccati 不等式時,目前尚沒有有效的方法找到最優(yōu)的李雅普諾夫函數(shù).這正是本文研究李雅普諾夫函數(shù)構造(或優(yōu)化)的動機.
令
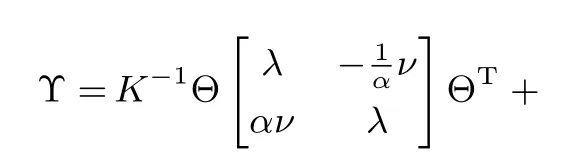

其中,α≥1,

ι>0,k≥1,0≤θ≤π/4.
由式(8)構造的李雅普諾夫函數(shù)分解了“放縮”和“旋轉”作用.這種功能的分解使李雅普諾夫函數(shù)的參數(shù)優(yōu)化具有了可行性.
定理1.對于系統(tǒng)(5),系統(tǒng)H∞范數(shù)γ滿足
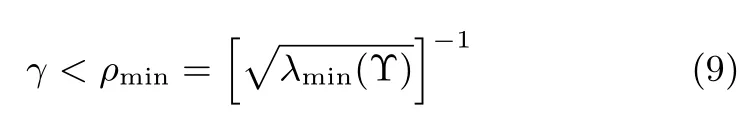
其中,λmin(Υ)為矩陣Υ 的最小特征值.
證明.令X=ΘTKΘ,其中,K和Θ 由 式(8)給出.根據(jù)特性2 和式(7),得
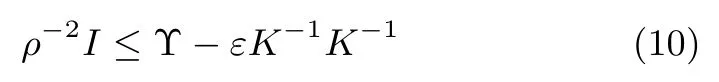
則ρ?2≤λmin(Υ?εK?1K?1),由于γ <ρ,并且ε為趨于零的正數(shù),則式(9)成立.
注2.根據(jù)定理1,可以優(yōu)化李雅普諾夫函數(shù)的參數(shù),以最大化λmin(Υ),進而精確估計系統(tǒng)H∞范數(shù).因此,定理1給出了一種新的途徑以得到系統(tǒng)的H∞范數(shù).
3 李雅普諾夫函數(shù)優(yōu)化
考查式(7)給出的矩陣Υ.由式(7)和式(8),可得
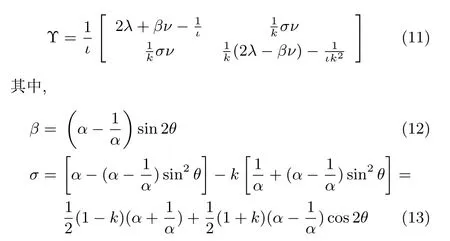
根據(jù)式(11),以最大化λmin(Υ)為目標,將給出一種李雅普諾夫函數(shù)的優(yōu)化方法.
3.1 李雅普諾夫函數(shù)優(yōu)化策略
令

則由式(7)和X=ΘTKΘ,得

其中,Λ=diag{σ1,σ2},σ1≥σ2,則

則根據(jù)Λ=diag{σ1,σ2},有σ1≥σ2,
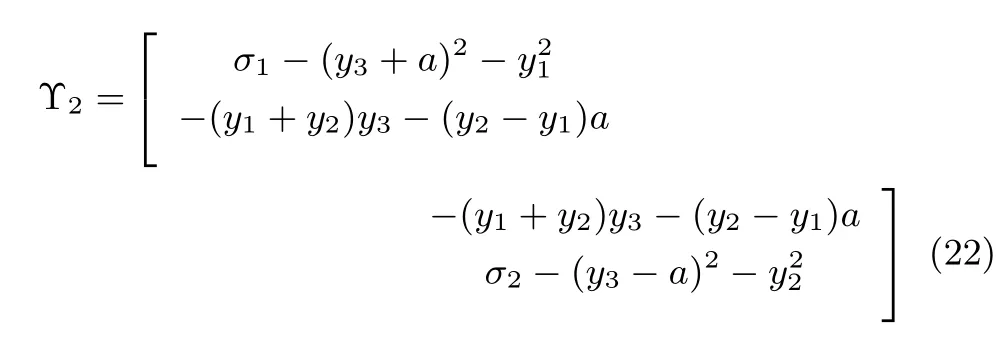
根據(jù)式(14),(16),(21),(22)和定理1,存在Y3,使λmin(Υ2)>0,即Υ2正定.因此根據(jù)式(22),為了最大化Υ2的最小特征值,應使下面兩個條件成立.
1)(y1+y2)y3+(y2?y1)a=0(例如y2=0,y3=a;或y1=y2=0).
2)Υ2的特征值相等(例如=σ1?σ2?4a2;或y3=(σ1?σ2)/4a).

基于以上分析,并根據(jù)式(9),(11),(14),(16)和(23),為了最大化Υ 的最小特征值,李雅普諾夫函數(shù)的優(yōu)化策略設計為σ=0 和λ1=λ2.
3.2 李雅普諾夫函數(shù)參數(shù)優(yōu)化
基于所給李雅普諾夫函數(shù)優(yōu)化策略,進一步優(yōu)化李雅普諾夫函數(shù)參數(shù).
定理2.對于系統(tǒng)(5),系統(tǒng)H∞范數(shù)γ滿足

其中,λ1和λ2由式(23)給出,式(23)中β由下式給出.
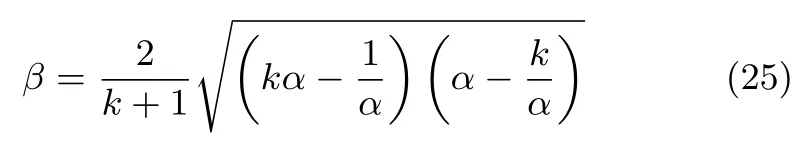
證明.考查式(11)給出的矩陣Υ.令σ=0,則

因此根據(jù)式(11),(12),(23)和0≤θ≤π/4,矩陣Υ 的特征值為λ1和λ2,其中β由 式(25)給出.根據(jù)定理1,可得式(24).
注3.基于李雅普諾夫函數(shù)參數(shù)矩陣Θ 的優(yōu)化策略,定理2 進一步給出系統(tǒng)H∞范數(shù)的估計.,同時奠定了進一步優(yōu)化李雅普諾夫函數(shù)參數(shù)k和ι的基礎.
定理3.對于系統(tǒng)(5),系統(tǒng)H∞范數(shù)γ滿足

其中,
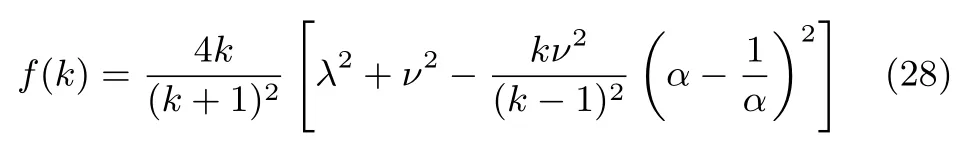
證明.考查式(23)給出的矩陣Υ 的特征值為λ1和λ2.令λ1=λ2,即

其中,β由 式(25)給出,α≥1.
當α>1 時,由 式(25)和式(29)可知k≠1,并且得

當α=1 時,由式(25)可知(k ?1)2≤0,即k=1.則根據(jù)式(23),(25),(29),當ι=λ時,得max(λ1)=λ2.
基于以上分析,并根據(jù)定理2 和式(23),(25),(29)以及(30),可得結論.
注4.通過給出李雅普諾夫函數(shù)參數(shù)ι的優(yōu)化策略,定理3 進一步給出系統(tǒng)H∞范數(shù)的估計.根據(jù)定理3,可以直接優(yōu)化李雅普諾夫函數(shù)參數(shù)k,進而得到系統(tǒng)H∞范數(shù)的精確估計.
注5.注意,當α>1 時,k≠1.因此定理3 通過分別討論α>1 和α=1 兩種情況,解決了f(k)的奇異問題.令

則由式(28),得

定理4.對于系統(tǒng)(5),系統(tǒng)H∞范數(shù)γ滿足
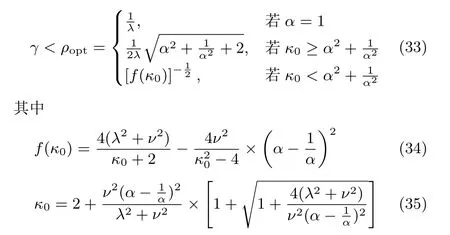
證明.由式(32),得

令f′(κ)=0,即

根據(jù)κ>2 和式(35),得κ=κ0.
根據(jù)式(35)~(37),得

因此,在2<κ<∞的條件下,maxf(κ)=f(κ0),如圖1(a)和1(b)所示.
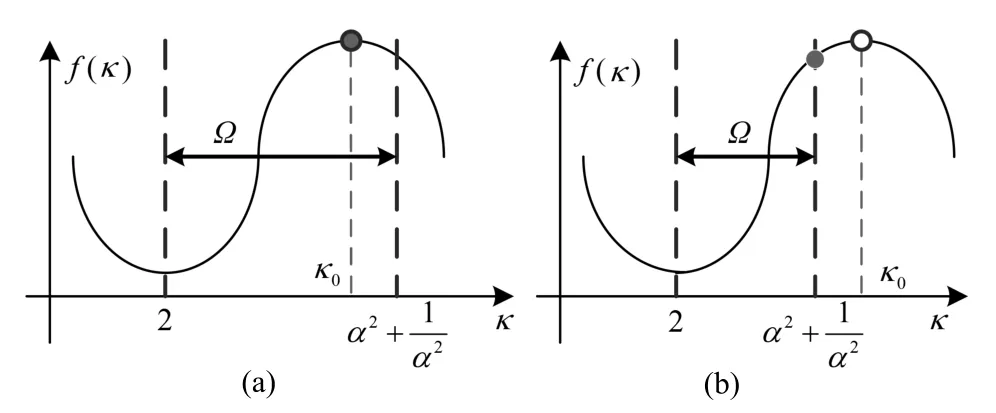
圖1 函數(shù)分析Fig.1 Function analysis
注意,定理2 中李雅普諾夫函數(shù)參數(shù)矩陣Θ 的優(yōu)化策略為σ=0,則由式(13),可得k≤α2.由于k >1,因此根據(jù)式(31),得

根據(jù)圖1(a)和1(b),得
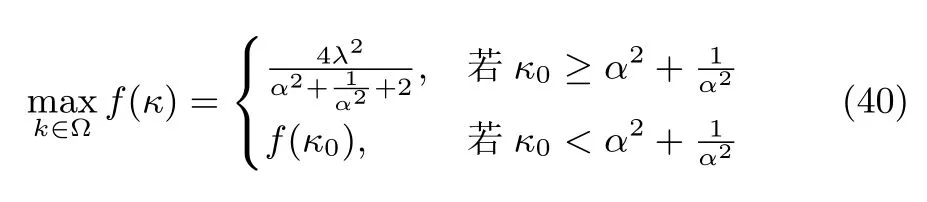
因此由定理3 可得結論.
注6.通過對李雅普諾夫函數(shù)參數(shù)的直接優(yōu)化,定理4給出了系統(tǒng)H∞范數(shù)上界的優(yōu)化結果.應用定理4,可以給出系統(tǒng)H∞范數(shù)的精確估計.
注7.不同于LMI 方法,本文提出的李雅普諾夫函數(shù)直接優(yōu)化方法分析了李雅普諾夫函數(shù)的構造對系統(tǒng)性能分析的影響,充分利用系統(tǒng)結構和參數(shù)以優(yōu)化李雅普諾夫函數(shù)的設計.與LMI 方法相比,李雅普諾夫函數(shù)直接優(yōu)化方法能夠直接給出系統(tǒng)H∞范數(shù)的精確結果,進而避免了復雜的數(shù)值優(yōu)化過程.因此本文的工作提供了一種新的途徑以更為方便地分析系統(tǒng)動態(tài)性能.
4 算例
考查系統(tǒng)
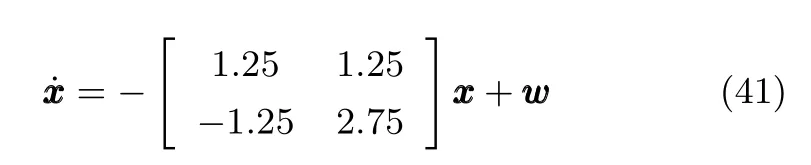
其中,w為擾動輸入,≤1,x為狀態(tài)輸出.根據(jù)式(5),得

因此,λ=2,ν=1,α=2.
由式(35),得κ0=3.8651<=4.25.則根據(jù)定理4,得γ <ρopt=0.622.因此γ≈0.622.應用MATLAB中H∞范數(shù)求解函數(shù)hinfnorm(sys,0.0000001)可得相同的結果.因此提出的李雅普諾夫函數(shù)直接優(yōu)化方法能精確給出系統(tǒng)H∞范數(shù).
表1 進一步給出在不同參數(shù)條件下系統(tǒng)(5)的H∞范數(shù).表1 表明,針對式(5)給出的具有不同參數(shù)的系統(tǒng),提出的李雅普諾夫函數(shù)直接優(yōu)化方法都能精確給出系統(tǒng)H∞范數(shù).
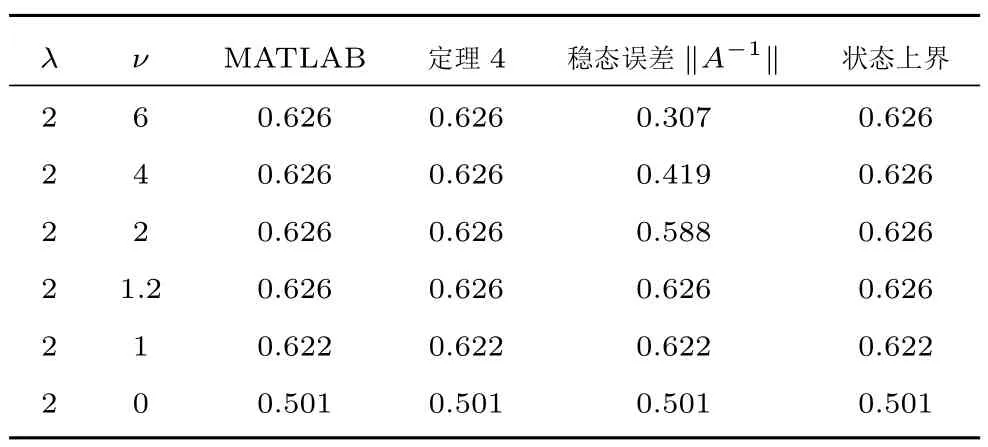
表1 H∞范數(shù)分析(α=2)Table 1 H∞norm analysis(α=2)
在α和系統(tǒng)特征值實部λ確定(即α=2,λ=2)的條件下,表1 給出的結果表明,隨著系統(tǒng)特征值虛部ν變化,H∞范數(shù)的變化具有一定規(guī)律性,表現(xiàn)為:
1)當ν=ν?=1.2(即κ0=α2+1/α2)時,H∞范數(shù)為
2)當ν <ν?(即κ0<α2+1/α2)時,H∞范數(shù)與穩(wěn)態(tài)指標一致;
3)當ν >ν?(即κ0>α2+1/α2)時,H∞范數(shù)為固定值(即H∞范數(shù)的值與ν無關),并且根據(jù)定理4,H∞范數(shù)的表達式非常簡潔.
由式(1),(3),(41),得
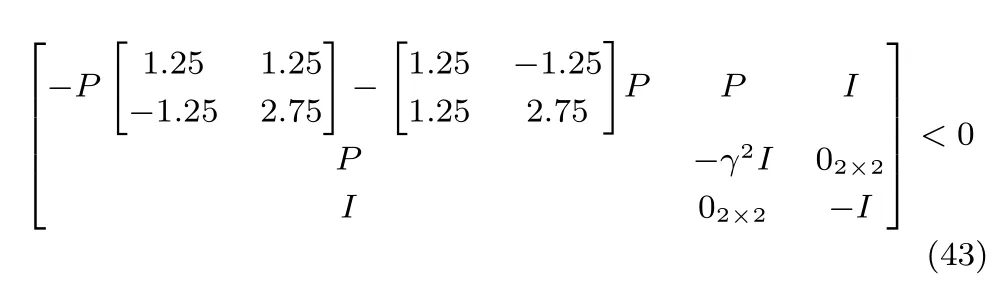
采用LMI 方法求解H∞范數(shù)的步驟為:
1)選擇足夠大的γ,如γ=10;
2)應用MATLAB 中LMI 工具求解式(43),可得P存在;
3)減小γ取值,如γ=1,應用LMI 工具求解式(43),可得P存在;
4)當γ=0.622 時,應用LMI 工具求解式(43),可得P存在;
5)當γ=0.621 時,應用LMI 工具求解(43),可得P不存在.
基于以上步驟,LMI 方法可給出H∞=0.622.這一結果與定理4 得到的結果一致,如表1 所示.
事實上,LMI 方法需要對γ進行遍歷尋找.當選γ的間隔較大時,保守的結果不可避免.與之相比,本文的方法具有明顯的優(yōu)越性.
5 結論
本文針對H∞控制理論研究中難以精確求解系統(tǒng)H∞范數(shù)的問題,提出了一種李雅普諾夫函數(shù)的直接優(yōu)化方法.通過優(yōu)化Riccati 不等式中的李雅普諾夫函數(shù),給出了H∞范數(shù)的通用解析表達式,進而提供了一個有效的途徑以直接和精確求解系統(tǒng)H∞范數(shù).研究結果具有以下特點:
1)與LMI 方法相比,本文所提方法避免了復雜的數(shù)值優(yōu)化過程,使求解系統(tǒng)H∞范數(shù)簡化.
2)與早期關于李雅普諾夫方程和Riccati 不等式的研究相比,本文所提方法避免了由于李雅普諾夫函數(shù)選擇的隨意性導致的保守結果.
3)本文所提方法能夠展現(xiàn)系統(tǒng)矩陣特征值的實部和虛部對H∞性能的影響,為進一步精確(定量)控制系統(tǒng)H∞性能提供借鑒.
在進一步的工作中,將研究含有時滯及非線性項的系統(tǒng).

