四川省成都實驗外國語學校(611731) 宿曉陽

眾所周知,不等式在數(shù)學中有重要的地位,無論是國際數(shù)學奧林匹克競賽(IMO)、世界各國(地區(qū))數(shù)學奧林匹克競賽,還是國內各大高校自主招生數(shù)學考試,與不等式有關的試題頻頻出現(xiàn).原因是不等式有各種難度,具有較強的挑戰(zhàn)性,不僅可以很好區(qū)分考試的水平,還可以反映考生的數(shù)學功底和創(chuàng)新水平.本文將給出幾個新穎的含有二次根式的三元不等式.供參考與欣賞.同時為我們的英才教育提供一點新鮮血液!

命題1設x,y,z是正實數(shù),則

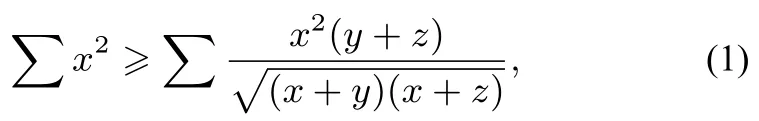
其中∑表示三元循環(huán)和.

證明在三角形嵌入不等式:x2+y2+中作代換,有:,再由三角形恒等式(其中a,b,c和s為分別為三角形的三邊和半周長),設s-a=x,s-b=y,s-c=z,則,于是有

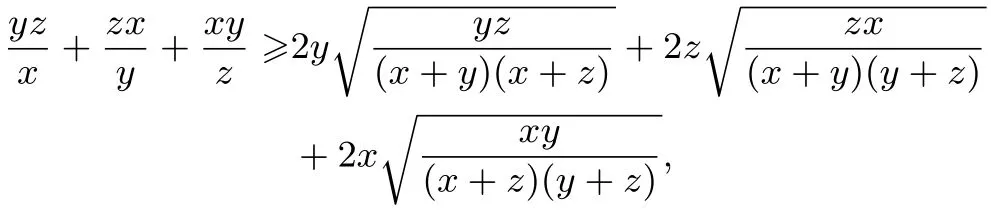
同理

兩個不等式相加,得

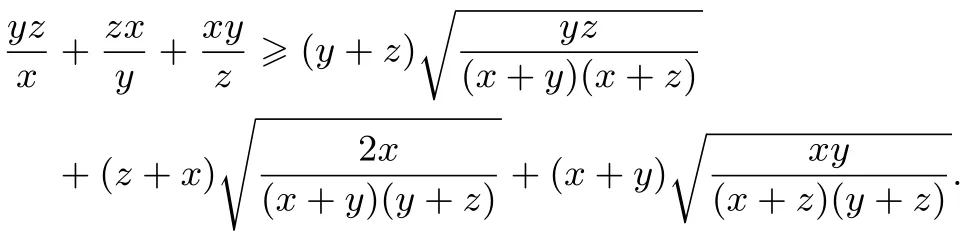
命題2設x,y,z是正實數(shù),則

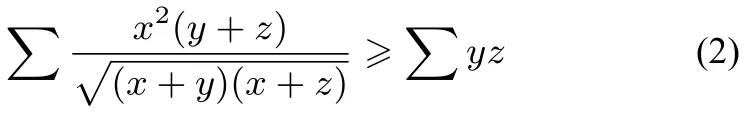
證明先證:

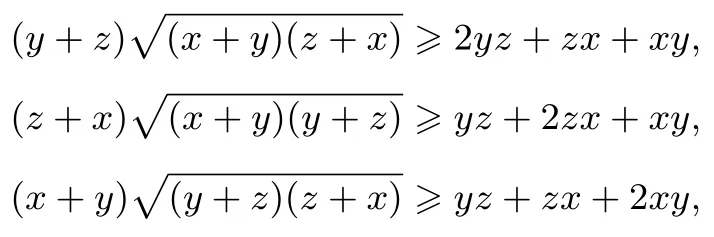
事實上,由二元柯西不等式,有

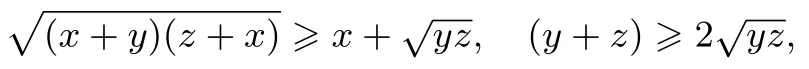
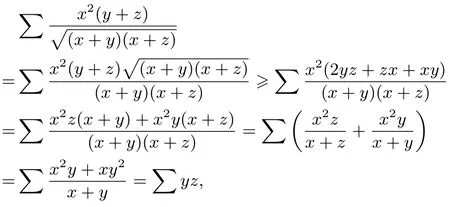
即(2)式成立.

注:由(1)和(2)式,我們得到一個有趣的不等式鏈:設x,y,z是正實數(shù),則.

命題3設x,y,z是正實數(shù),則

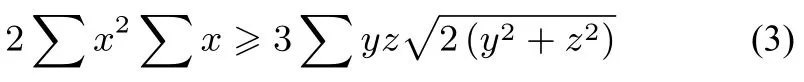
證明由柯西不等式,有

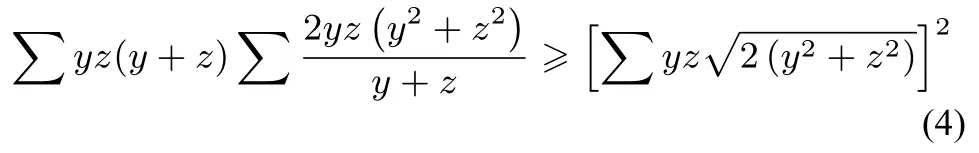
由(4)式知欲證(3)式,即證

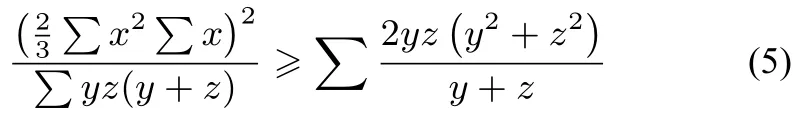
證

事實上,(6)式等價于

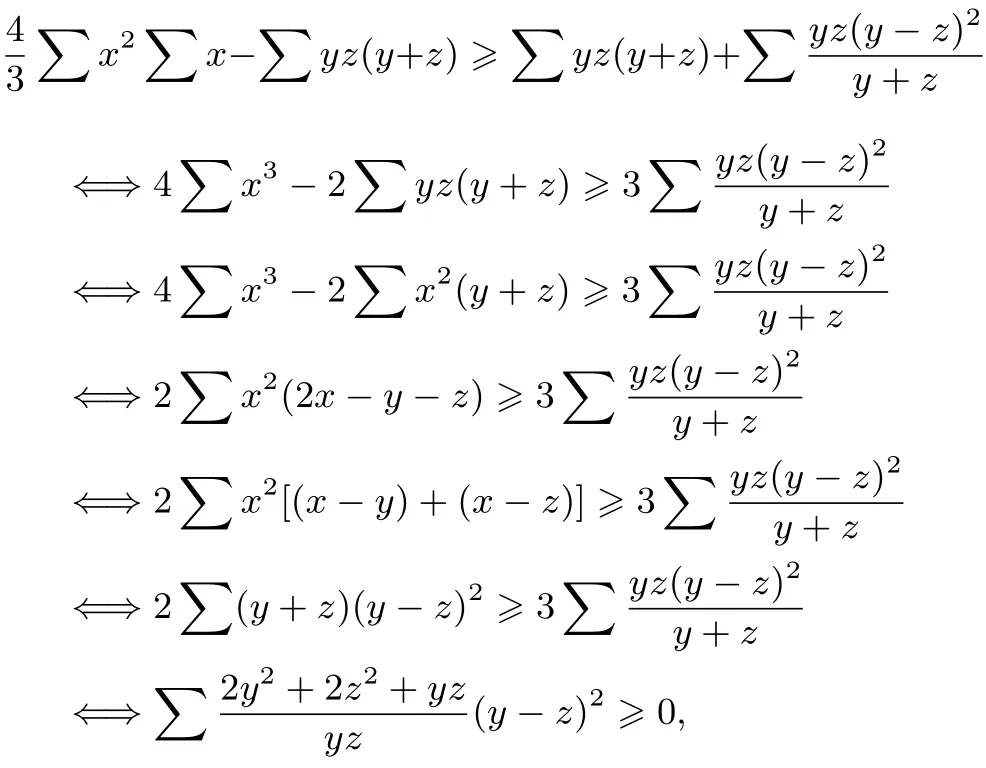
此不等式顯然成立,即(6)式成立,于是(3)式得證.

注:命題3類似于2004mosp不等式:設x,y,z是正實數(shù),則

有興趣的讀者不妨利用上述方法試一試.

命題4設x,y,z是正實數(shù),則

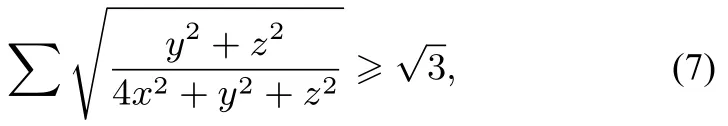
其中∑表示三元循環(huán)和.

證明先證:

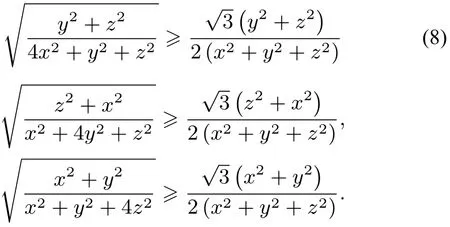
事實上,(8)式等價于

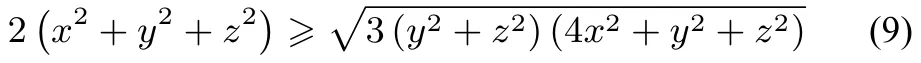
由二元均值不等式,有

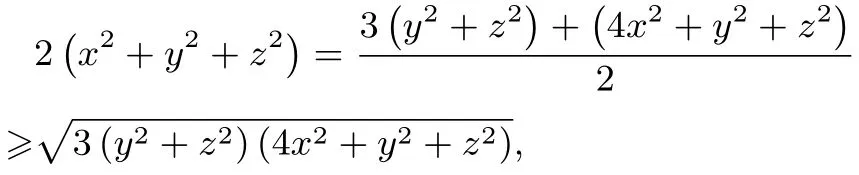
即(9)式成立.所以(8)式成立.同理可證明另外倆式.于是由上述三式相加即得(7)式.

注:命題4強于不等式:設x,y,z是正實數(shù),則

命題5設x,y,z是正實數(shù),則

證明(10)式兩邊平方,(10)等價于

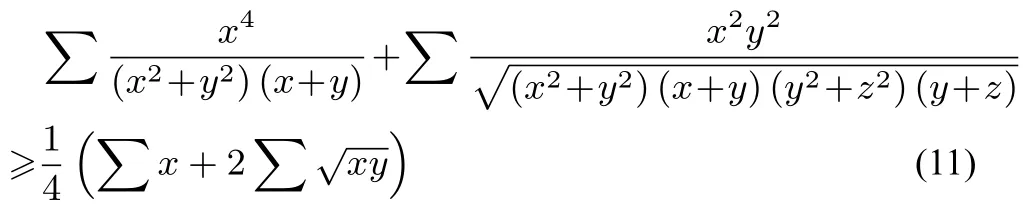
由排序不等式,有

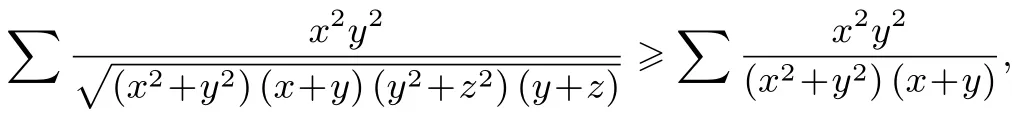
于是由上式知,欲證明(11)式,即證明

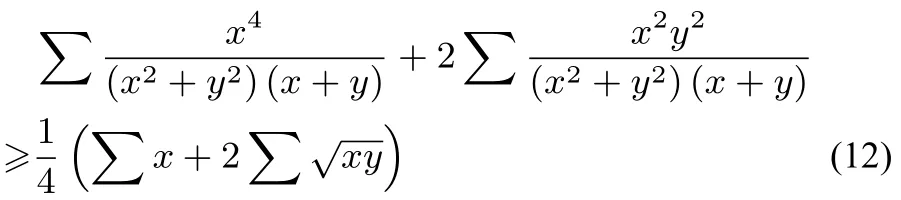
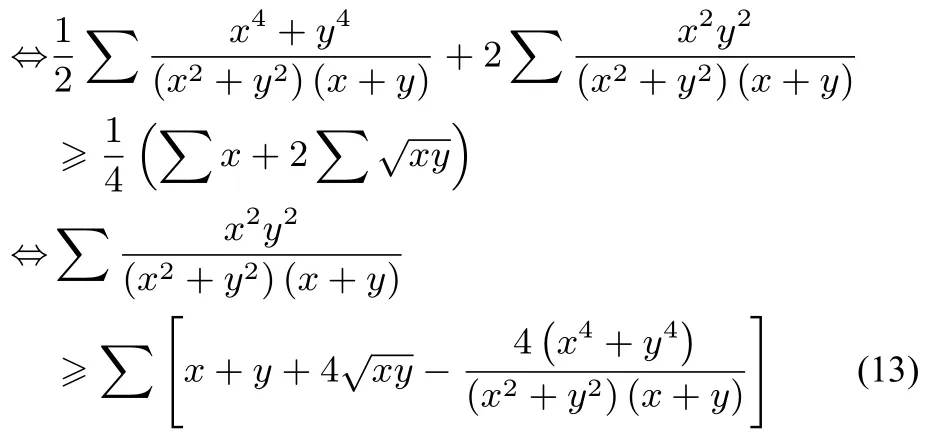
欲證明(11)式,即證明

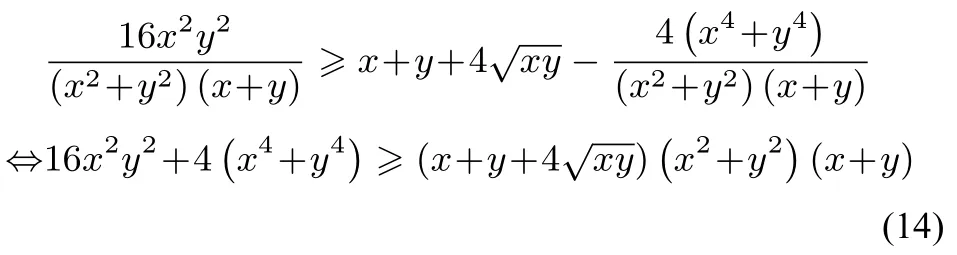
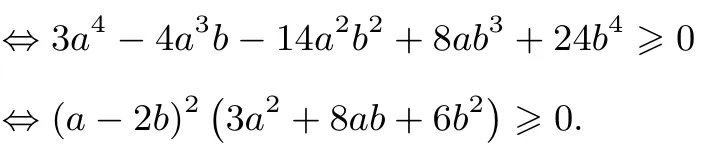
此式顯然成立,即(13)式成立.故(10)式得證.

注:命題5類似于1988年Walther Janous在加拿大數(shù)學雜志Curx提出了如下問題:設x,y,z是正數(shù),求證:

此題曾被選為2014年印度尼西亞國家集訓隊選拔考試題.