MA Peng-yu,DU Bo

(epartment of Mathematics,Huaiyin Normal University,Huaian Jiangsu,223300,China)

Abstract:A generalized neutral stochastic functional differential equation(NSFDE)with Markovian switching is studied.We will discuss some important properties of the solutions including boundedness and exponential stability by using Lyapunov-Krasovskii functional,Matrix inequality and some analysis techniques.Finally,an numerical example for neutral stochastic neural networks with Markovian switching is given to show the effectiveness of the results in this paper.

Key words:eutral;It?o formula;Markov chain;Stability

§1. Introduction

In the past decade,NSFDEs have attracted considerable attention because of their numerous applications in model identification,pattern recognition,signal processing,optimization,etc.Since they are very important in the development of theory and practice,the asymptotic properties of NSFDEs have been considered by several authors,see e.g.[1-10]and the references therein.

On the other hand,many hybrid systems may undergo abrupt changes in their structure and parameters caused by phenomena such as component repairs or failures,changing subsystem interconnections,and abrupt environmental baffles.The hybrid systems driven by continuoustime Markov chains have recently been developed to deal with such cases.The systems combine a part of the state that takes values continuously and another part of the state that takes discrete values.Recently,some results have been obtained for NSFDEs with Markovian switching.For example,Liu,Wang and Liu[11]concerned a class of Markovian jumping neutral neural networks with mode-dependent mixed time-delays:

Kolmanovskii,Koroleva etc.[12]studied neutral stochastic differential delay equations and established a fundamental theory for such systems,furthermore discussed some important properties of the solutions for boundedness and exponential stability.More detailed results on NSFDEs with Markovian switching could be found in[13-20]and the references therein.

So far,to the best of the authors’knowledge,there is few results for the asymptotic properties of NSFDEs with Markovian parameters.The major challenges list as follows:(1)in order to construct a feasible Lyapunov functional,the properties of neutral operator A(defined in(2.2))can be considered.So,studying the properties of the operator A seems very important;(2)when the Markovian parameters exist in NSDDEs,the corresponding stability problems become more complicated since a new Lyapunov functional is required to reflect Markovian chain’s influence;and(3)it is non-trivial to establish a unified framework to handle the Markovian parameters,neutral terms and delays influence.It is,therefore,the main purpose of this paper to make the first attempt to handle the listed challenges.

Throughout the manuscript,(?,F,}Ft}t≥0,P)is a complete probability space with a filtration{Ft}t≥0satisfying the usual conditions(i.e.it is right continuous and F0contains all P-null sets),ω(t)=(ω1(t),···,ωm(t))>is an m-dimensional Brownian motion defined on the probability space,Rnand Rn×mdenote,respectively,the n-dimensional Euclidean space and the set of all n×m real matrices.The superscript“>”denotes the matrix transposition.We will use the notation A>0(or A<0)to denote that A is a symmetric and positive definite(or negative definite)matrix.If A,B are symmetric matrices,A>B(A≥B),then A?B is a positive definite(positive semi-definite).|z|denotes the Euclidean norm of a vector z and|A|denotes the induced norm of the matrix A,that iswhere λmax(·)means the largest eigenvalue of A.E[x]means the expectation of x.

The remaining structure of this paper is arranged as follows.In section 2,we consider the model formulation and preliminaries.Section 3 deals with asymptotic boundedness for the present model.In section 4,we study the exponential stability for the present model.A numerical simulation is presented to illustrate our theoretical results in section 5.Finally,conclusions are drawn in section 6.

§2. Model Description and Preliminaries

Let r(t)(t≥0)be a right-continuous Markovian chain taking values in a finite sate space S={1,2,···,n0}with generator Π ={πij}given by

Here ? >0 and πij≥ 0 is the transition rate from i to j if i 6=j andand C([?τ,0];Rn)be he family of continuous function with the norm||φ||=sup?τ≤θ≤0|φ(θ)|.Let p>0 and([?τ,0];Rn)denote the family of all Ft-measurable C([?τ,0];Rn)?valued random variables φ such that sup?τ≤θ≤0E|φ(θ)|p< ∞.

In this paper,we deal with the following NSFDE with Markovian switching

the mappings f,g:Rn×Rn×S are all Borel-measurable functions.Let the inial data of(2.1)

Remark 2.1 shows the neutral character by the operator A,which is different from other papers,see e.g.[3-4,6,8].

Remark 2.2 When C=0,Eq.(2.1)is changed into a non neutral-type system which has been extensively studied,see e.g.[1,10].

Lemma 2.1 If c+<1,then the inverse of difference operator A denoted by A?1,exists and

where c+=max{|c1|,|c2|,···,|cn|},c?=min{|c1|,|c2|,···,|cn|}.

In view of|B|<1,the operator A exists a unique inverse operator A?1and

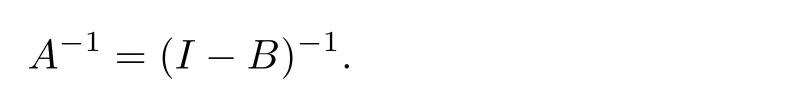
Thus,

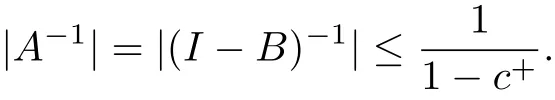
On the other hand,by the definition of c?,we have

The proof is completed.

Lemma 2.2(Generalized It?o formula)[16]Let V∈C2,1(Rn×R+×S;R)and x(t)be a solution of(2.1).Then for any stopping times 0≤ ρ1≤ ρ2< ∞ a.s.

where LV:Rn×R+×S→R is defined by

Lemma 2.3[16]Assume that W ∈Rn×nis a positive-definite matrix and U ∈ Rn×nis a symmetrical matrix.Then,for any x∈Rn,we have

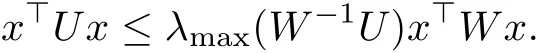
Definition 2.1 Equation(2.1)is said to be asymptotically bounded in pth moment if there is a constant H>0 such that

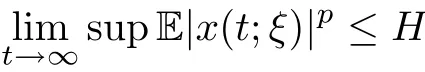
Definition 2.2 The trivial solution of equation(2.1)is said to be exponential stability in pth moment if there exist constants λ,C>0 such that

Remark 2.3 In order to obtain the existence and uniqueness of solution to equation(2.1),according to[12],in what follows we will impose the following assumptions on f and g:Assume that that there exists a positive constant K such that

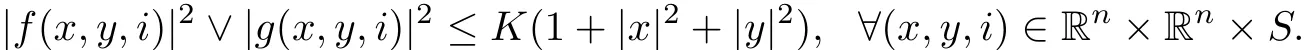
Moreover,for every h>0,there is a positive constant Khsuch that

§3.Asymptotic Boundedness

We need the following assumptions.There exist positive constants λ1,λ2and β such that

From Remark 2.1,we know that the solution x(t,ξ)satisfies

For p=2,we will show that(3.1)holds as t→∞.

Theorem 3.1 Let c+<1,C+=:.Assume that assumptions(H1)and(H2)hold.Letˉγ>0 be the unique solution to the equation

where where α1=mini∈Sλmin(Qi),α2=maxi∈Sλmax(Qi),α3=maxi,j∈Sλmax(Qj),Qi(i∈S)is symmetric positive-definite matrices with proper dimensions.Then Eq.(2.1)is asymptotically bounded in mean square.

Proof Let V∈C2,1(Rn×R+×S;R+)and

where Qi(i∈S)is symmetric positive-definite matrices with proper dimensions.Obviously,

From(2.3),Lemma 2.1,Lemma 2.3,assumptions(H1)and(H2),we have

Using the generalized It?o formula,(3.4)and(3.5),we derive

In view of(3.2),there exists γ∈(0,ˉγ]such that

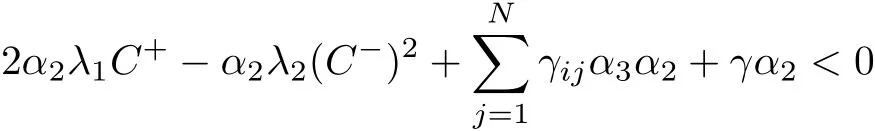
which together with(3.6)we have

Thus,by(3.4),(3.7)and Lemma 2.1,we have

Since T>0 is arbitrary,by(3.8)we have

§4. Exponential stability

In this section,we assume that f(0,0,r(0))=g(0,0,r(0))=0,then Eq.(2.1)admits a trivial solution x(t)=0 for t≥ ?τ.We need the following assumption:there exist positive constant λ such that

(H3)|f(x,y,i)|∨|g(x,y,i)|≤λ|x|, ?(x,y,i)∈Rn×Rn×S.

Theorem 4.1 Let c+<1 and assumption(H3)hold.Then the trivial solution x(t)=0 of Eq.(2.1)is pth moment exponential stability,if for each i∈S,the following condition is satisfied:

where α is a positive constant,p ≥ 1,and Qi(i∈ S)is symmetric positive-definite matrices with proper dimensions.

Proof Consider the following Lyapunov-Krasovskii functional:

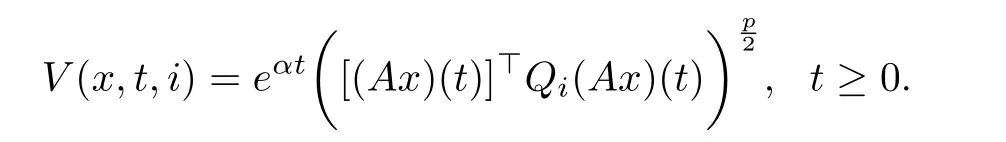
From(2.1),assumption(H3),Lemma 2.1 and Lemma 2.3,we have

By(4.1),we have

For any t,t?≥ 0,and t>t?,applying Dynkins formula to(4.2),we obtain

It follows from the mathematical induction that for every i,l∈ S,t>t?,

Remark 4.1 In this paper,the Asymptotic properties of NFDEs are studied.The distinctive contributions of this paper are outlined as follows:(1)when the neutral delay term is studied as a neutral operator A,novel analysis technique is developed since the conventional analysis tool no longer applies;(2)a new Lyapunov functional is constructed to reflect the neutral operator and Markovian switching;(3)a unified framework is established to handle the stochastic parameters,neutral terms and delays.

§5. Application for Neutral Stochastic Neural Networks with Markovian Switching

To show the effectiveness of the results,we give an practical application for neutral stochastic neural networks with Markovian switching.

Example 5.1 Consider a two-dimensional neutral stochastic neural networks with Markovian switching:

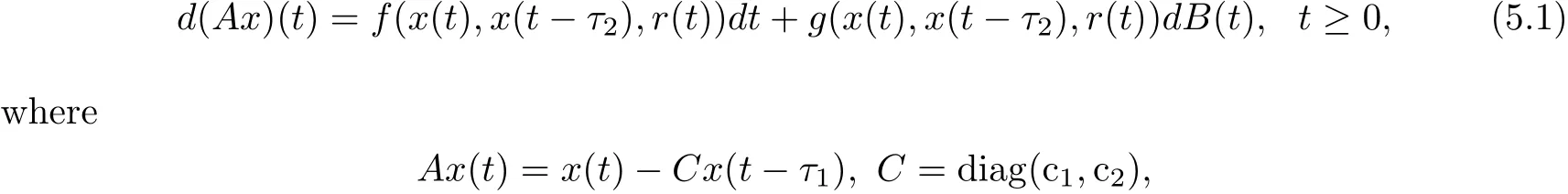
x(t)=(x1(t),x2(t))>,B(t)is a one-dimensional Brownian motion and the Markov process{r(t),t≥0}taking values in S={1,2}with generator

Hence,by Theorem 4.1,Eq.(5.1)is exponential stability in the mean square with its Lyapunov exponent not greater than 0.5.The simulation results show that Eq.(5.1)is exponential stability in the mean square(see Fig.1).

Remark 5.1 We very want to give the answer to the circuit diagram of Eq.(2.1).However,(2.1)contains neutral operators and Markovian switching,is more complicated.So far,we can not obtain the circuit diagram of(2.1).We hope that some authors research this subject in the future.

Figure 1:State trajectories of Eq.(5.1).

§6. Preliminaries

In this article,using Lyapunov-Krasovskii functional,Matrix in-equality and some analysis techniques,we study a generalized neutral stochastic functional differential equation with Markovian switching.It is noted that our results can be used for the research of neutral stochastic neural networks with Markovian switching.However,many important questions about NSFDE with Markovian switching remain to be studied,among them optimal control,dynamic properties for complex networks,global stability,and bifurcation problrms.