Lyapunov-type inequalities for fractional differential systems with more than three monomials
QI Yong-fang,HAN Li-tao,WEI Xu-ting
(1.School of Mathematics,Pingxiang University,Pingxiang,Jiangxi,337000,P.R.China;2.School of Information,Renmin University of China,Beijing 100080,P.R.China;3.School of Mathematics and statistics,Lanzhou Jiaotong University,Lanzhou,Gansu,730070,P.R.China)
Abstract:This paper presents Lyapunov-type inequalities for fractional differential systems with more than three monomials by using the Gronwall-Inequality and the Greens function.The results of this paper extend the research methods of similar problems and generalize some early conclusions on this topic.In addition,with the help of the results,we can analyze the solution of differential systems.
Key words:Gronwall-Inequality;Lyapunov-type inequality;Fractional differential system;Boundary value problem
§1. Introduction
Fractional differential systems have gained great importance due to their applications in physics,mechanic and engineering,etc.There has been a significant development in fractional differential systems,see[1-6].In recent years,more and more Lyapunov-type inequalities for fractional differential equations under boundary conditions were established.
In[7],R.A.C.Ferreira considered the following fractional boundary value problem,
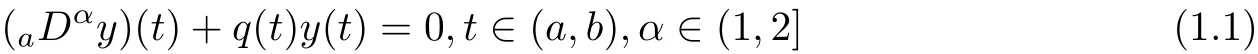
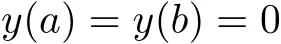
If it has a nontrivial solution,where q is a real and continuous function,aDαis the Riemann-Liouville fractional derivative,then

In[8],R.A.C.Ferreira have discussed the following Caputo fractional boundary value problem,
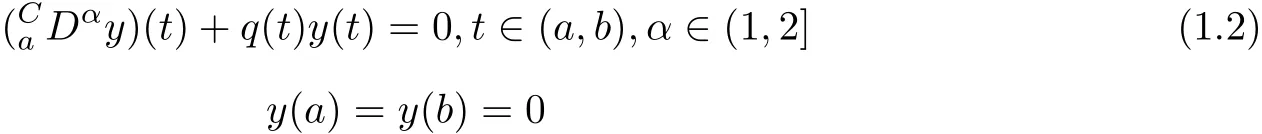
where q is a real and continuous function,if the system(2)has a nontrivial solution,then
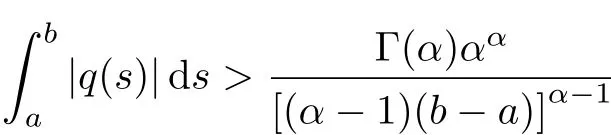
Since then,a great amount of useful and important results were obtained.
In[9],Rong Ji considered a Caputo fractional differential equation under boundary conditions involving the Caputo fractional derivative problem,
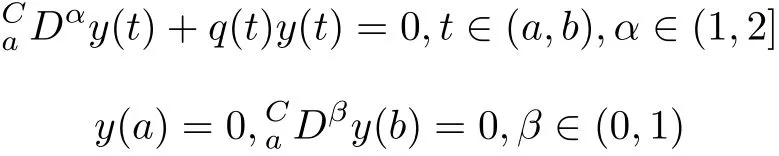
If a nontrivial continuous solution of the problem exists,then
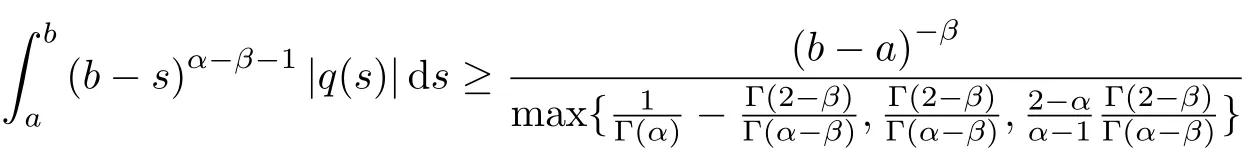
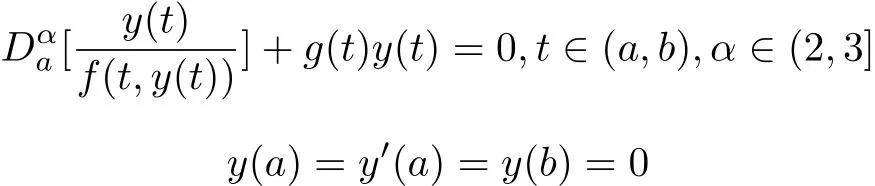
The necessary condition for the existence of a nontrivial solution for the boundary value problem is
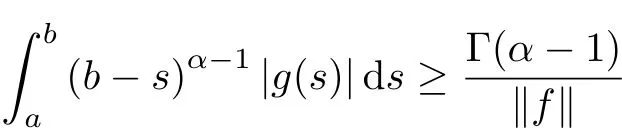
In[10],Sitho et al.considered the following interesting problem,
where kfk=supt∈[a,b],y∈R|f(t,y)|.
Nowadays,more and more authors pay attention to the higher order equations and the nonlinear system,such as[11]and[12].In[11],ORegan et al.studied the following fractional boundary value problem,
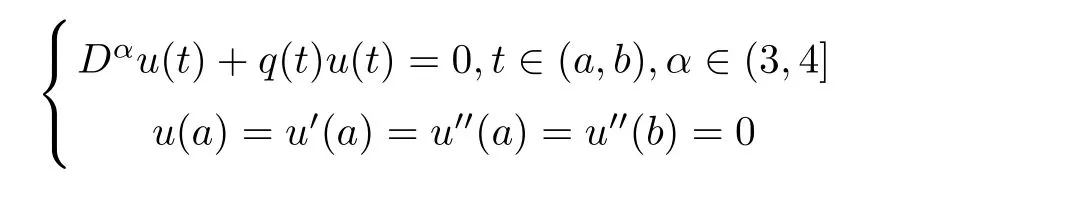
If a nontrivial continuous solution to the FBVP above exists,then,
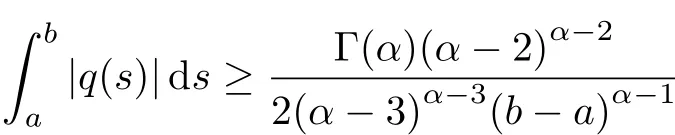
In[12],Chidouh et al.focused on the following nonlinear boundary value problem,
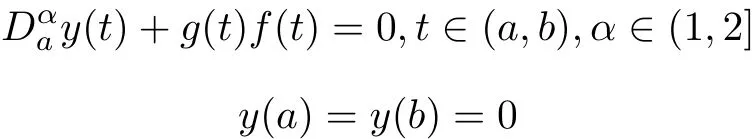
The author got an interval where the problem given above has at least one nontrivial positive solution.More and more Lyapunov-type inequalities for fractional differential equations under boundary conditions were obtained[13-16].But all of these Lyapunov-type inequalities given above were obtained by the Green’s function,and there are only two monomials in the systems.This paper attempts to make use of Gronwall-Inequality to get the Lyapunov-type inequality for the systems with more than three monomials.More precisely,the following Riemann-Liouville fractional differential equation is considered,
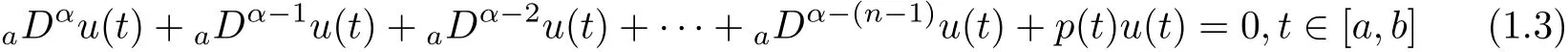
where n?1<α≤n,p:[a,b]→R is a continuous function.
§2. Preliminaries
In this section,we introduce preliminary facts and some basic results,which are used throughout this paper.
Definition 2.1[17]Letα>0 and f be a real function defined on[a,b].The Riemann-Liouville fractional integral of order is defined byaI0f≡f,and
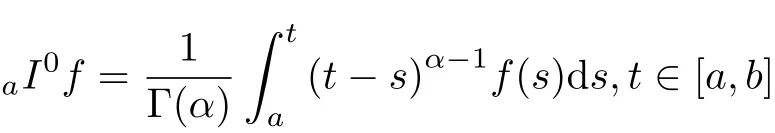
Definition 2.2[17]The Riemann-Liouville derivative of fractional order α>0 is defined byaI0f≡f,and
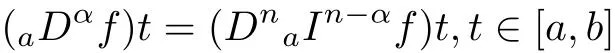
where n is the smallest integer greater or equal to α.
Lemma 2.1[17,p.36]If Dkf is continuous function on[a,b],then the following equality holds for t∈[a,b].
aIpaDqf(t)=Dq?pf(t)+a1(t? a)p?1+a2t? ap?2+a3(t? a)p?3+ ···+ak(t? a)p?khere,k?1≤q Lemma 2.2 (Gronwall-Inequality)Let K>0,f(t),g(t)≥0 and f(t),g(t)are continuous functions when t∈[a,b].If the following inequality holds, then, Lemma 2.3[7]If the Green’s function G(t,s)defined as following, then, Starting by writing the following fractional order boundary value problem in its equivalent integral form. Theorem 3.1 If u(t)is a nontrivial continuous solution of the Riemann-Liouville fractional boundary value problem Proof According to the fractional calculus theory(see[17]p.36),it is obtained that Combing with(3.3)(3.4)and(3.5),the equation(3.1)can be transformed into the following equation, where c1=b1+d1.By the boundary conditions of u(a)=u0(a)=0,then c1=b2=0. Hence where ku(t)k∞=max{|u(t)|},t∈ [a,b].With the lemma2.2(Gronwall-Inequality)given above,the following inequality is obtained, The inequality above holds for every t∈[a,b].Therefore, Theorem 3.2 If u(t)is a nontrivial continuous solution of the Riemann-Liouville fractional boundary value problem, Proof According to the fractions calculus theory(see[17]p.36),the equation(15)can be transformed into the following equation, By the boundary conditions of u(a)=u(b)=0,thenc3=0 with the result of Lemma 2.3,it is obtained that, where ku(t)k=sup{|u(t)|},t∈[a,b].Hence, Because of(3.12),it is obvious that the proof is completed. Theorem 3.3 If u(t)is a nontrivial continuous solution of the Riemann-Liouville fractional boundary value problem, Proof According to the fractions calculus theory(see[17]p.36),it is obtained that Combing with(3.15)(3.16)(3.17)and(3.18),the equation(3.13)can be transformed into the following equation, where c4=b3+d2+e1,c4=b4+d3.By the boundary conditions of u(a)=u0(a)=u00(a)=0,then c4=c5=b5=0 where ku(t)k∞=max{|u(t)|},t∈ [a,b].With the lemma(Gronwall-Inequality)given above,the following inequality is obtained, With the same method of theorem 3.3,it is easy to get the following theorem. Theorem 3.4 If u(t)is a nontrivial continuous solution of the Riemann-Liouville fractional boundary value problem, then the system(8)together with the boundary conditions u(a)=u0(a)=0 in Theorem 3.1 has no nontrivial solution. Corollary 2 Assume then the system(3.7)together with the boundary conditions u(a)=u(b)=0 in theorem 3.2 has no nontrivial solution. Corollary 3 Assume then the system(3.13)together with the boundary conditions u(a)=u0(a)=u00(a)=0 in Theorem 3.3 has no nontrivial solution. This paper enriches the research field of Lyapunov-type inequality and fractional differential systems.It studies the fractional differential systems with more than three monomials and provides a new method to handle the related problems.Further investigating in the future is focused on the Lyapunov-type inequalities for higher order fractional differential equations with Gronwall-Inequality way,and the application of the Lyapunov-type inequality in the reality.
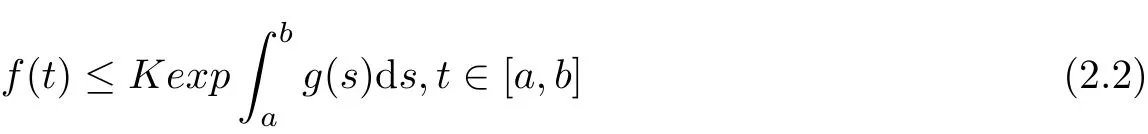
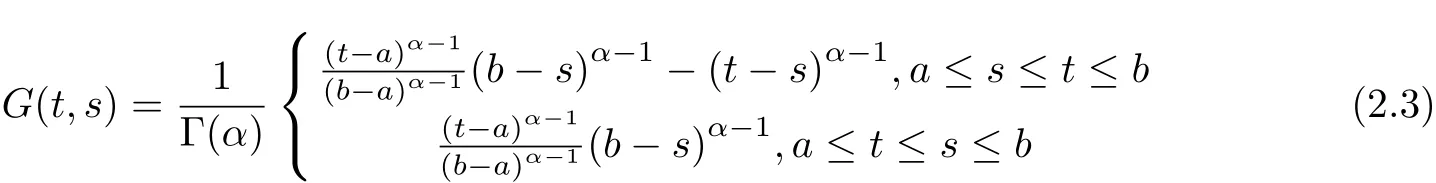
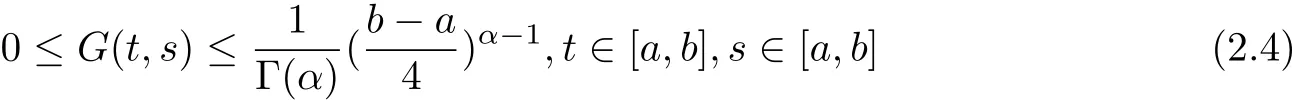
§3. Main Results
3.1 Case 1<α≤2
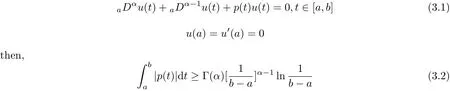
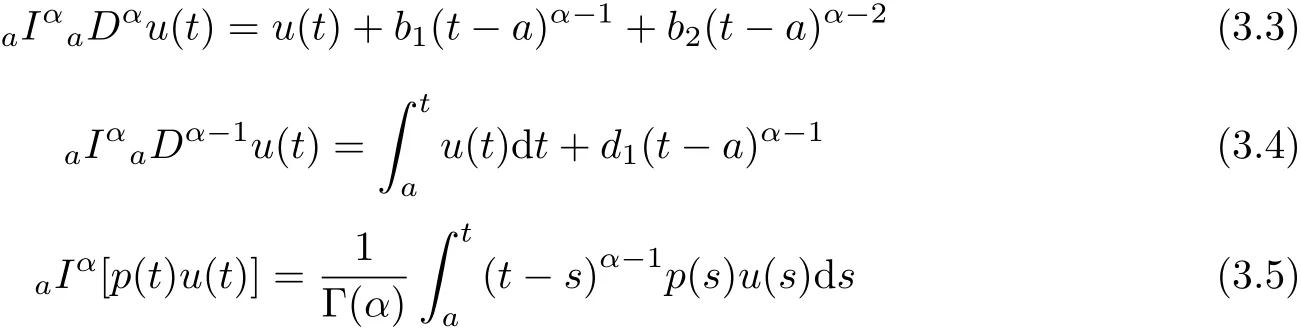
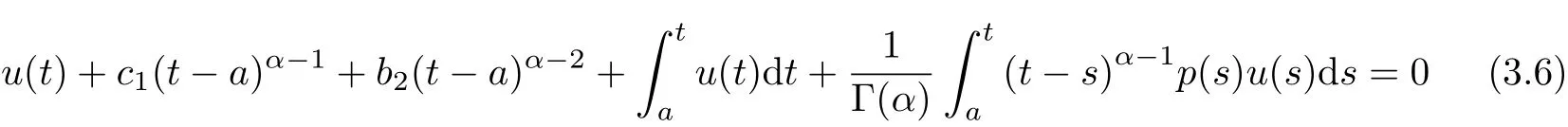
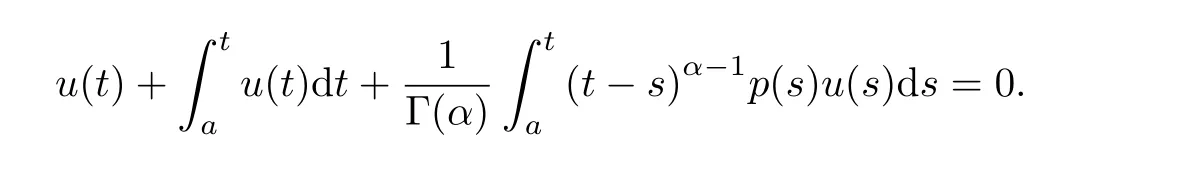
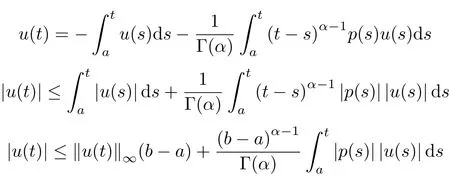
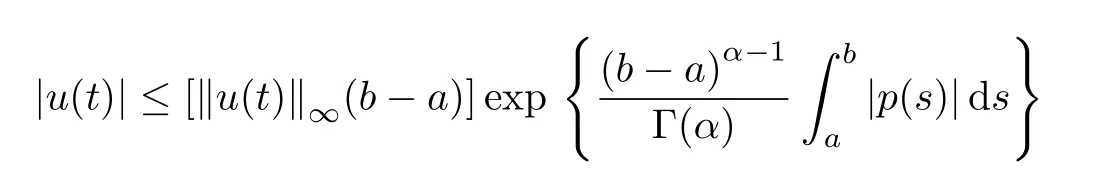
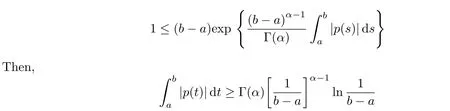
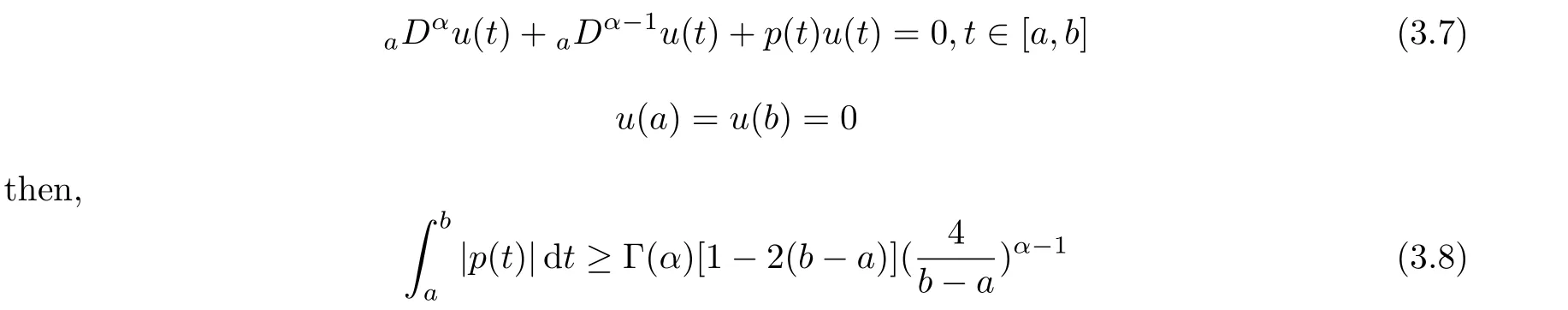
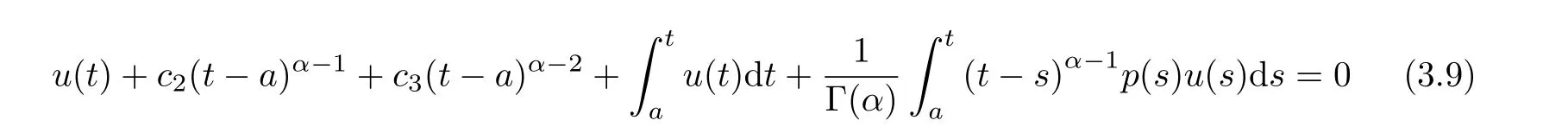
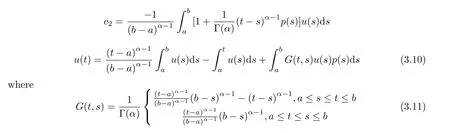

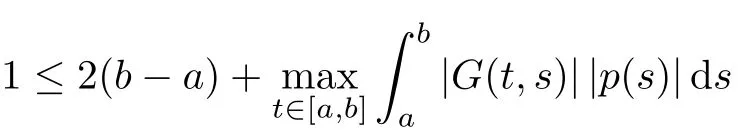

3.2 Case 2<α≤3
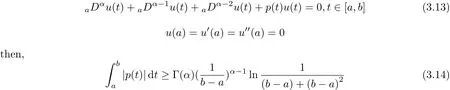
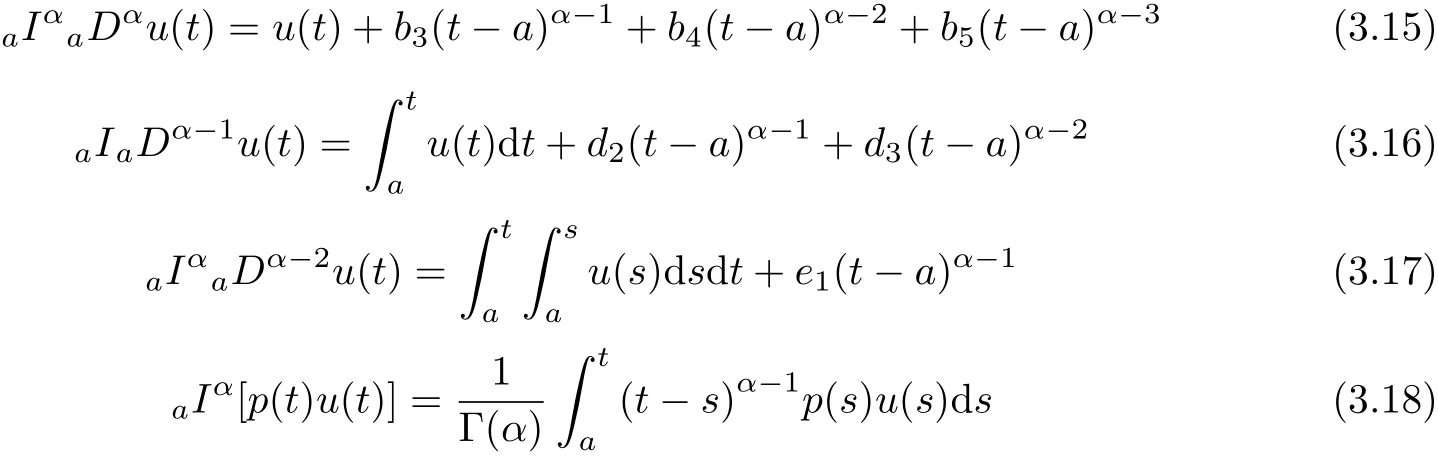

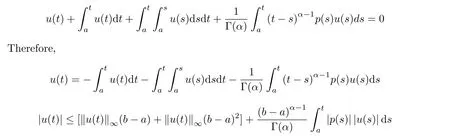
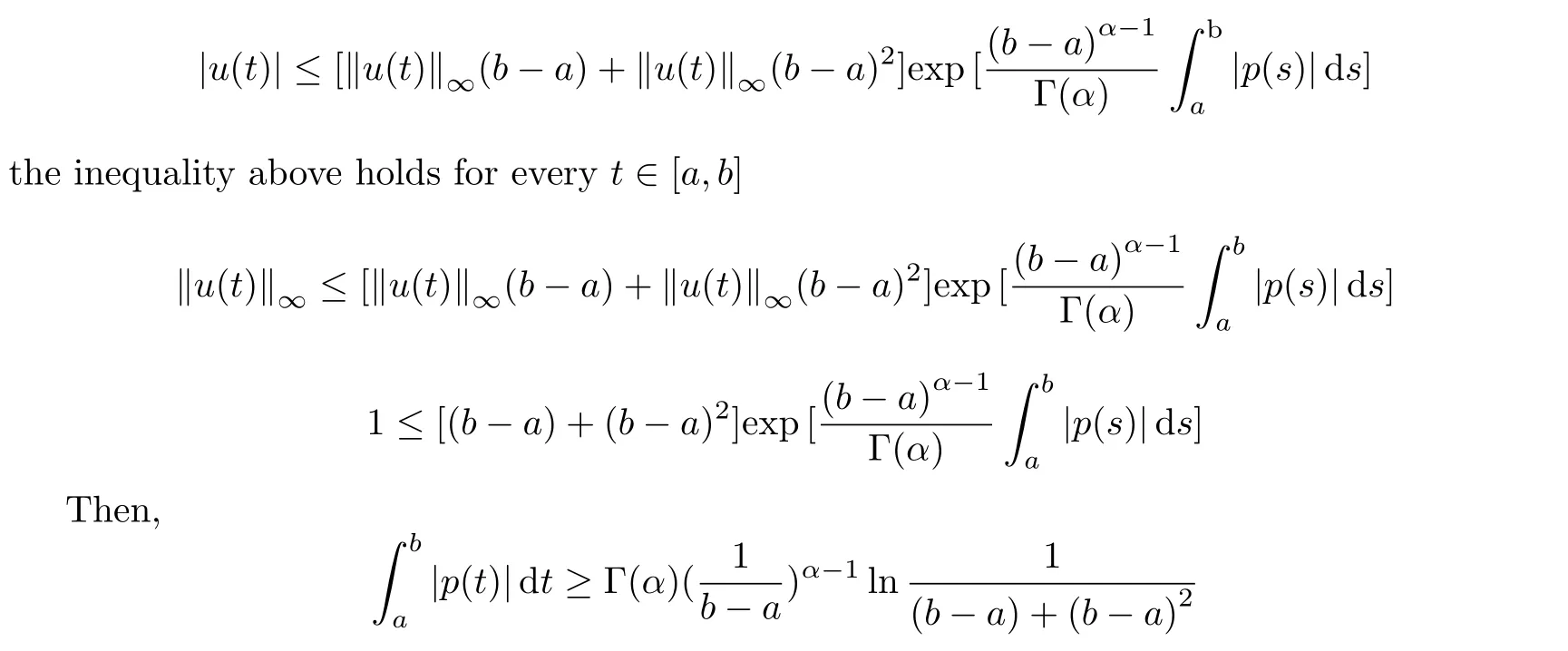
3.3 Case n?1<α≤n,n≥4
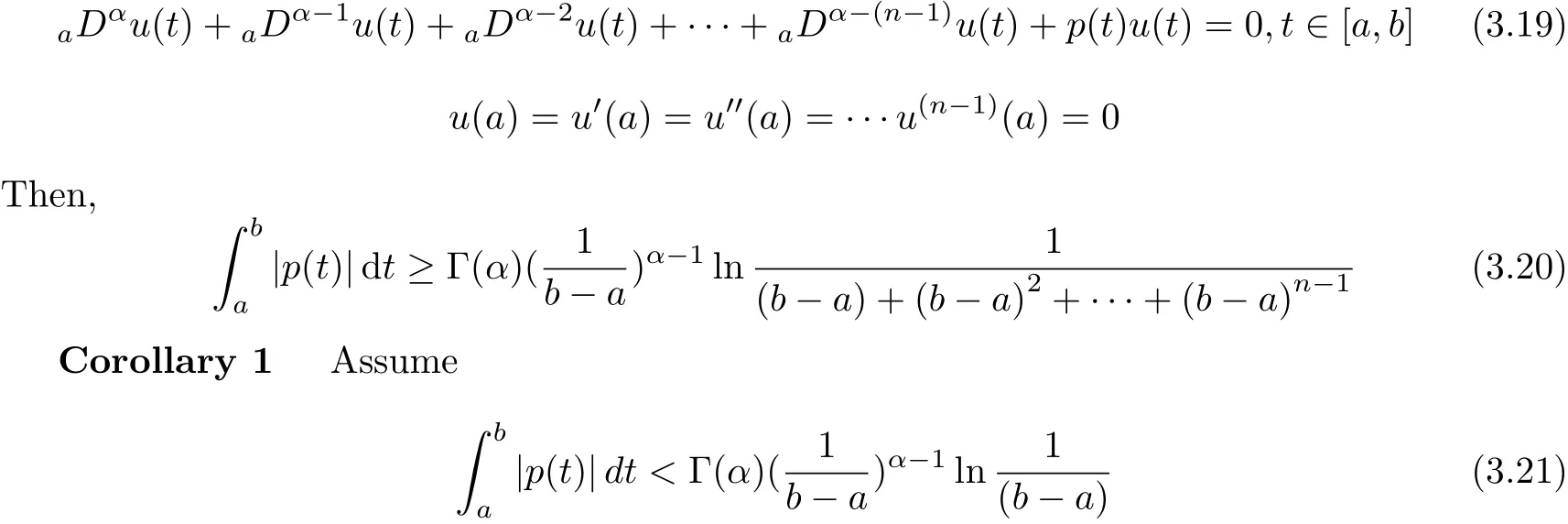
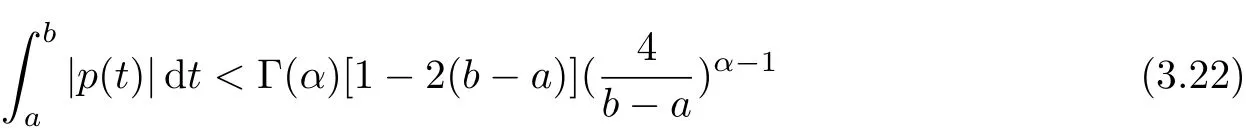
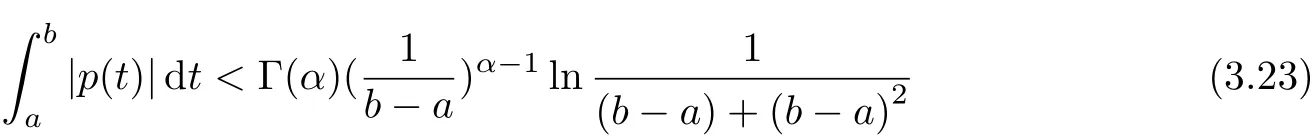
§4. Conclusions
 Chinese Quarterly Journal of Mathematics2018年3期
Chinese Quarterly Journal of Mathematics2018年3期
- Chinese Quarterly Journal of Mathematics的其它文章
- Dynamic Properties of Neutral Stochastic Differential Equations with Markovian Switching
- Fuzzy Stability of the Orthogonal Cauchy Functional equations
- The Maschke-type Theorems of Yetter-Drinfeld Hopf Algebras
- Generalizations of Hermite-Hadamard Type Inequalities Involving S-convex Functions
- Estimation of Derivatives for Bounded Regular Vanishing Functions
- Strongly α-Reflexive Rings Relative to a Monoid
