Generalizations of Hermite-Hadamard Type Inequalities Involving S-convex Functions
LIAN Tie-yan,TANG Wei
(1.College of Light Industry Science and Engineering,Shaanxi University of Science&Technology,Xi’an 710021,P.R.China;2.College of Electrical&Information Engineering,Shaanxi University of Science&Technology,Xi’an 710021,P.R.China)
Abstract:Some new Hermite-Hadamard type’s integral equations and inequalities are established.The results in[3]and[6]which refined the upper bound of distance between the middle and left of the typical Hermite-Hadamard’s integral inequality are generalized.
Key words:Hermite-Hadamard’s integral inequality;s-convex function;H¨older’s integral inequality
§1. Introduction
Let R be the set of real numbers,I?R,Iobe the interior of I.The following is the definition of convex functions which is well known knowledge in mathematical literature:f:I→R is said to be convex on an interval I if the inequality
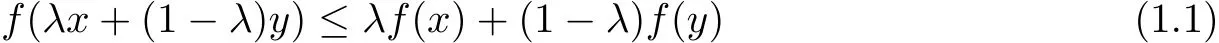
holds for all x,y∈I and λ∈[0,1].
For convex function,many equalities or inequalities have been established but the Hermite-Hadamard’s integral inequality is one of the most important,which is stated as follow[1]:
If f:I→R is a convex function on I and a,b∈I with a In[2],S.S.Dragomir gave the upper bound of distance between the middle and left of the typical Hermite-Hadamard’s integral inequality for functions whose derivatives absolute values are convex functions. Theorem 1.1[2]Let f be defined on I and differentiable on Iosuch that a,b∈I with a In[3],M.A.Latif and S.S.Dragomir refined the above result. Theorem 1.2[3]Let f be defined on I and differentiable on Iosuch that a,b∈I with a In[4],Orlicz introduced the definition for s?convexity of real valued mappings.In[5],Hudzik and Maligranda considers,among others,the class of mappings which are s?convex in the second sense.This class is defined as follows: Definition 1.1 A mapping f:I? R+=[0,∞)→ R is said to be s?convex in the second sense on I if the inequality holds for all x,y∈I and for some fixed s∈(0,1]. It is easy to observe that for s=1,the class of s?convex in the second sense is merely the class of convex mappings defined on[0,∞). In[6],Jaekeun Park established the following result which also gives a refinement of(1.3): Theorem 1.3[6]Let f be a differentiable mapping on the interior Ioof an interval I such that f0∈L([a,b]),where a,b∈I with a A number of papers have been written on Hermite-Hadamard’s integral inequality(1.3),providing new proofs,noteworthy extensions,generalizations,refinements and numerous applications.For the further results on this Hermite-Hadamard’s integral inequalities we also can refer to[7-15]and the references therein. The main aim of this paper is to establish some new Hermite-Hadamard’s integral inequalities which give an estimate betweenfor mappings whose derivatives absolute value are s?convex in the second sense.As a consequence we will get refinements of(1.3),(1.4)and(1.5). For establishing some new integral inequalities of Hermite-Hadamard type for functions whose derivatives absolute value are convex,we need some integral equality below.First of all,we begin with the following Lemma. Lemma 2.1 Let f be defined on I and differentiable on Iosuch that a,b∈I with a Proof By integration by parts and by making use of the variable substitution x=ta+(1?t)b we get the disired result. Theorem 2.1 Let f be defined on I and differentiable on Iosuch that a,b,x,y∈I with a By adding(2.2)-(2.5),we get the desired equatity(2.1). Corollary 2.1 Let f be defined on I and differentiable on Iosuch that a,b∈I with a Using Corollary 2.1 and letting m=r?1,we have Corollary 2.2,which was obtained in[6].And using Corollary 2.2,Jaekeun Park established their main results including inequality(1.5)which mentioned above. Corollary 2.2 Let f be defined on I and differentiable on Iosuch that a,b∈I with a Corollary 2.3 Let f be defined on I and differentiable on Iosuch that a,b∈I with a Proof For(2.1),if we choose x=y,then we have(2.8). Basing on equalities in section 2,we now start out to establish some integral inequalities of Hermite-Hadamard type for functions whose derivatives absolute value are s?convex. Theorem 3.1 Let f be a differentiable mapping on the interior Ioof an interval I such that f0∈L([a,b]),where a,b∈I with a Using the s?convexity of|f0|in the second sense on[a,b],we have the following inequalities hold: By using(3.3)-(3.6)in(3.2),we have inequlity(3.1). Corollary 3.1 Suppose all the condition of Theorem 3.1 are satisfied.If we choosein Theorem 3.1,then we have Similar to the proof of Theorem 3.1,inequality(3.7)can also be obtained by using Corollary 2.1 and the s?convexity of|f0|in the second sense on[a,b].Let m=r?1 in inequality(3.7),and we get inequality(1.5)which was a main result in[6].Let r=4,m=3 in inequality(3.7),and we get a same inequality as literature[3]. Theorem 3.2 Let f be a differentiable mapping on the interior Ioof an interval I such that f0∈L([a,b]),where a,b∈I with a Proof Using Theorem 2.1 and the well-known H¨older integral inequality for q>1,andwe have Using the s?convexity of|f0|qin the second sense on[a,b],we observe that the following inequality holds: By using(3.10)-(3.14)in(3.9),we get the desired result. Corollary 3.2 Suppose all the condition of Theorem 3.2 are satisfied.If we choose Similar to the proof of Theorem 3.2,inequality(3.8)can also be obtained by using Corollary 2.2 and the s?convexity of|f0|in the second sense on[a,b].If we let m=r?1 in inequality(3.8),we get inequality which was another main result in[6].Let r=4,m=3 in inequality(3.8),and we get a same inequality as literature[3]. Theorem 3.3 Let f be a differentiable mapping on the interior Ioof an interval I such that f0∈L([a,b]),where a,b∈I with a Proof Using Theorem 2.1 and the well-known power-mean inequality,we have By using(3.17)-(3.20)in(3.16),we get the desired result. Corollary 3.3 Suppose all the condition of Theorem 3.3 are satisfied.If we choosein Theorem 3.3,then we have We can obtain an inequality of[6]for letting m=r?1 in(3.21).Meanwhile,a result of[3]is obtained for r=4,m=3.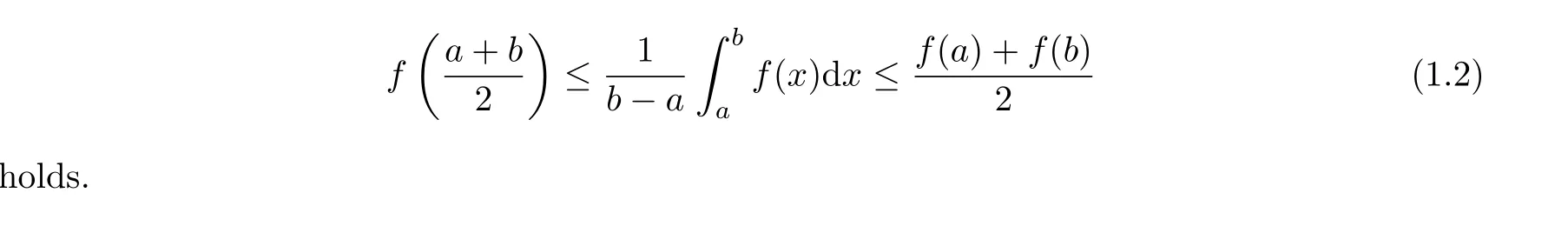
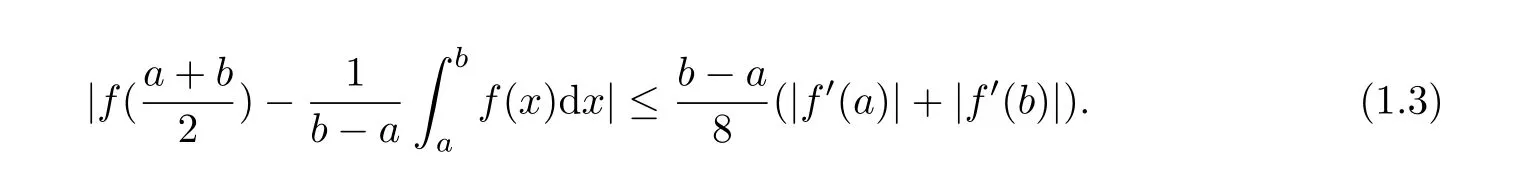
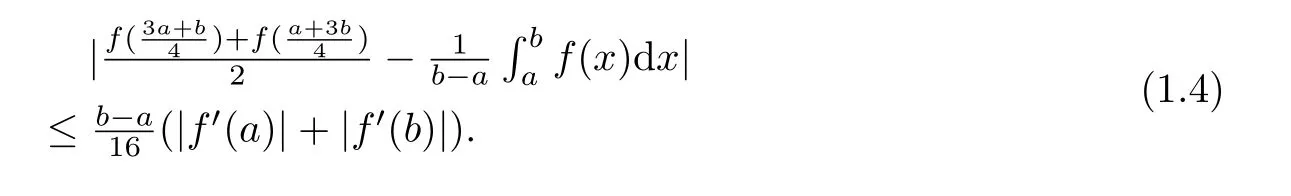
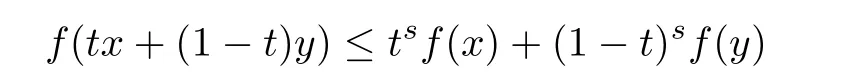
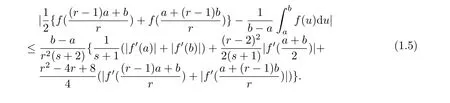
§2. Some integral equality aboutRbaf(x)dx

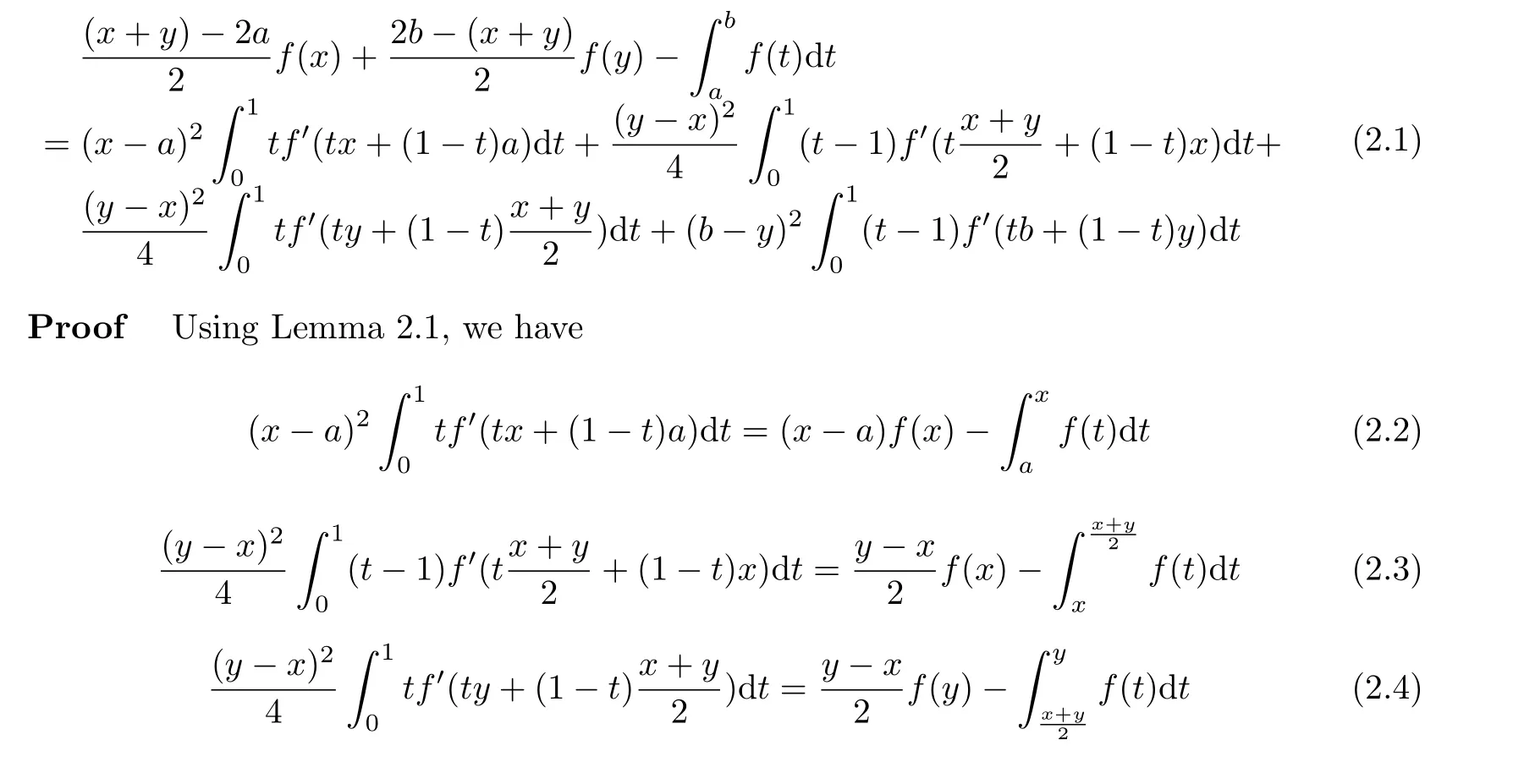
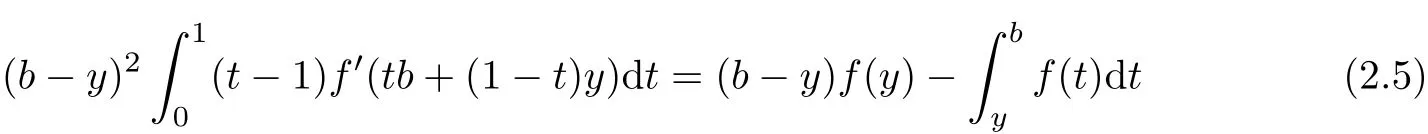
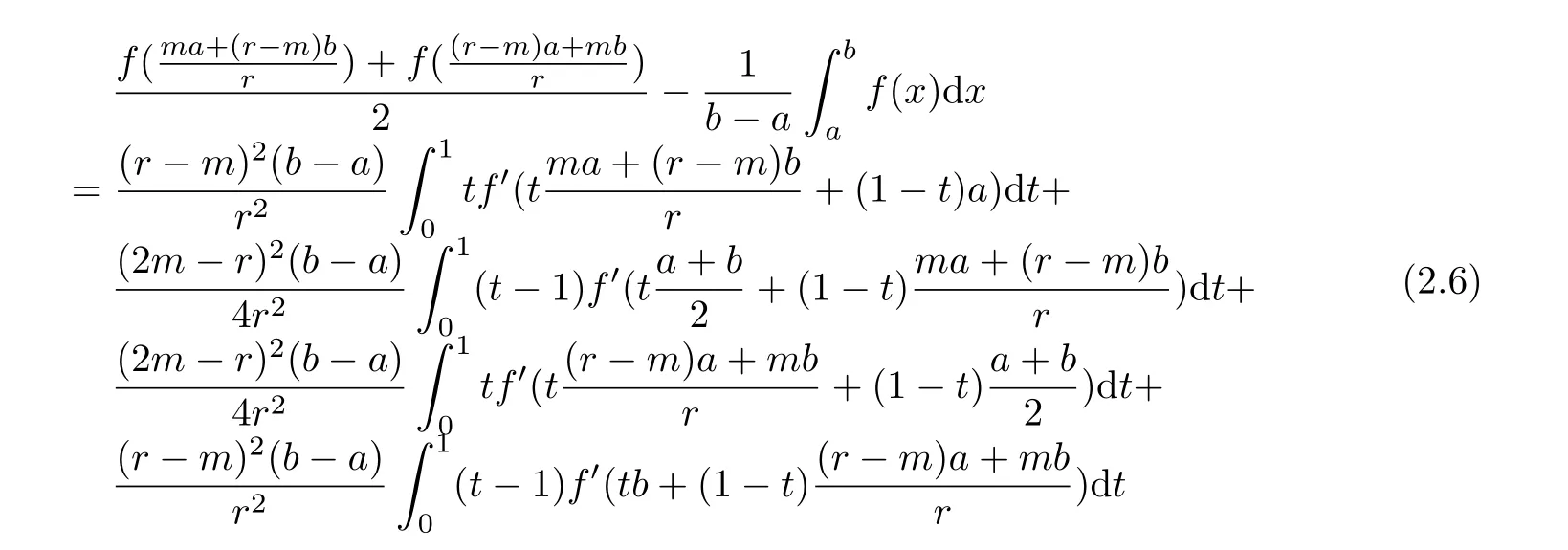
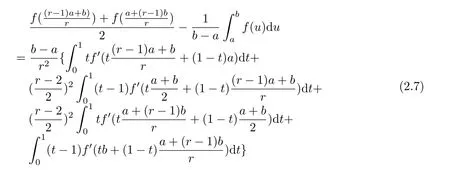
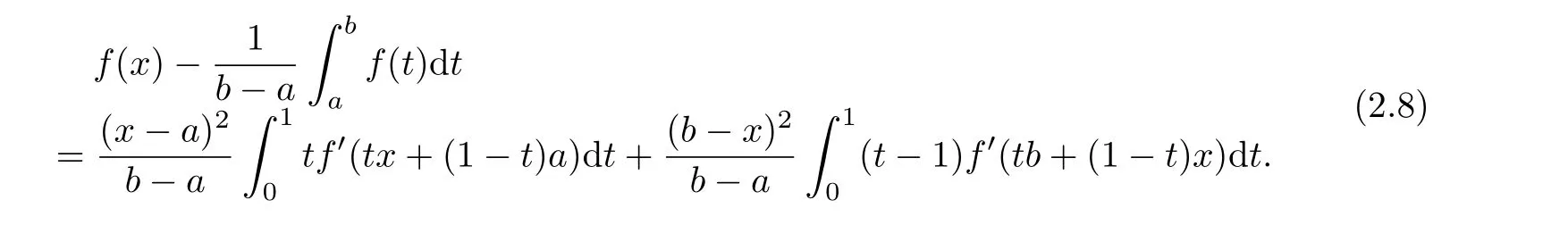
§3.New Inequalities About Hermite-Hadamard’s Integration for s?convex Functions

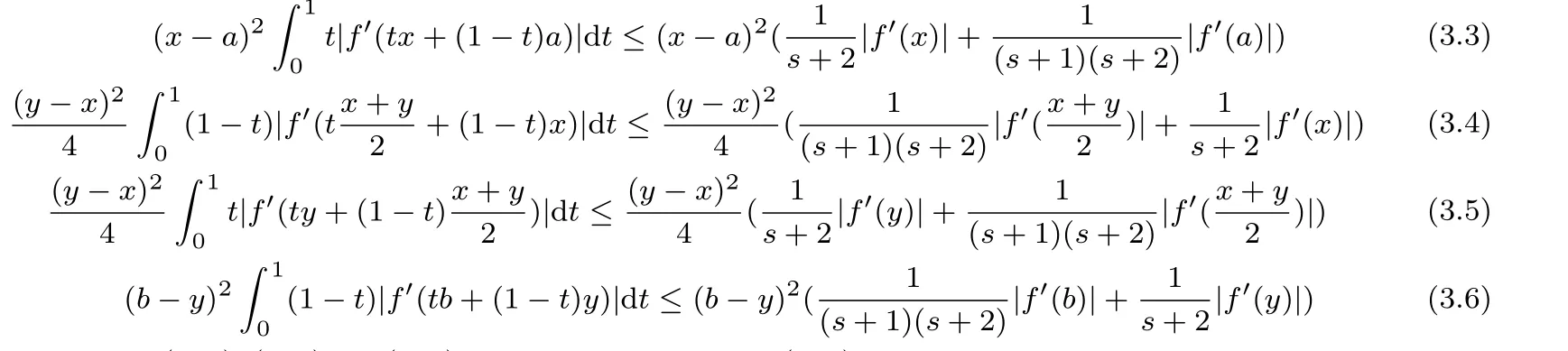
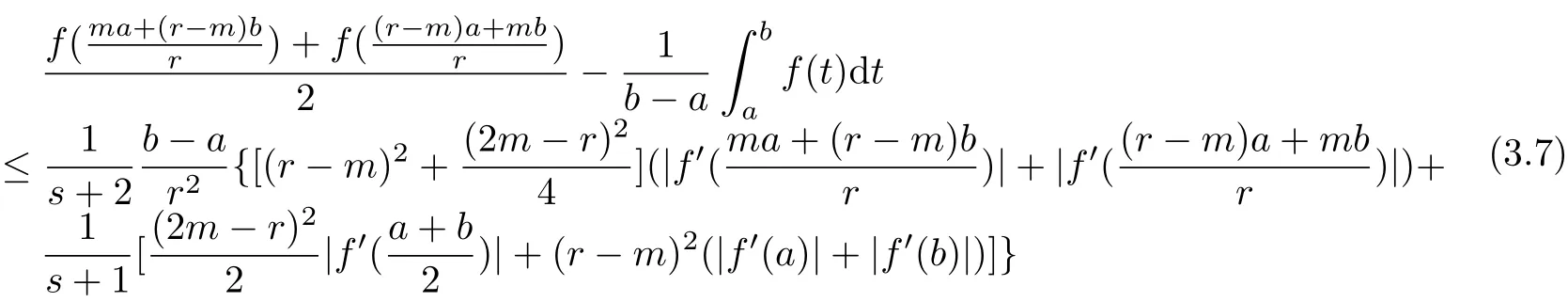
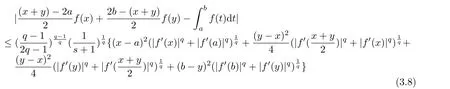

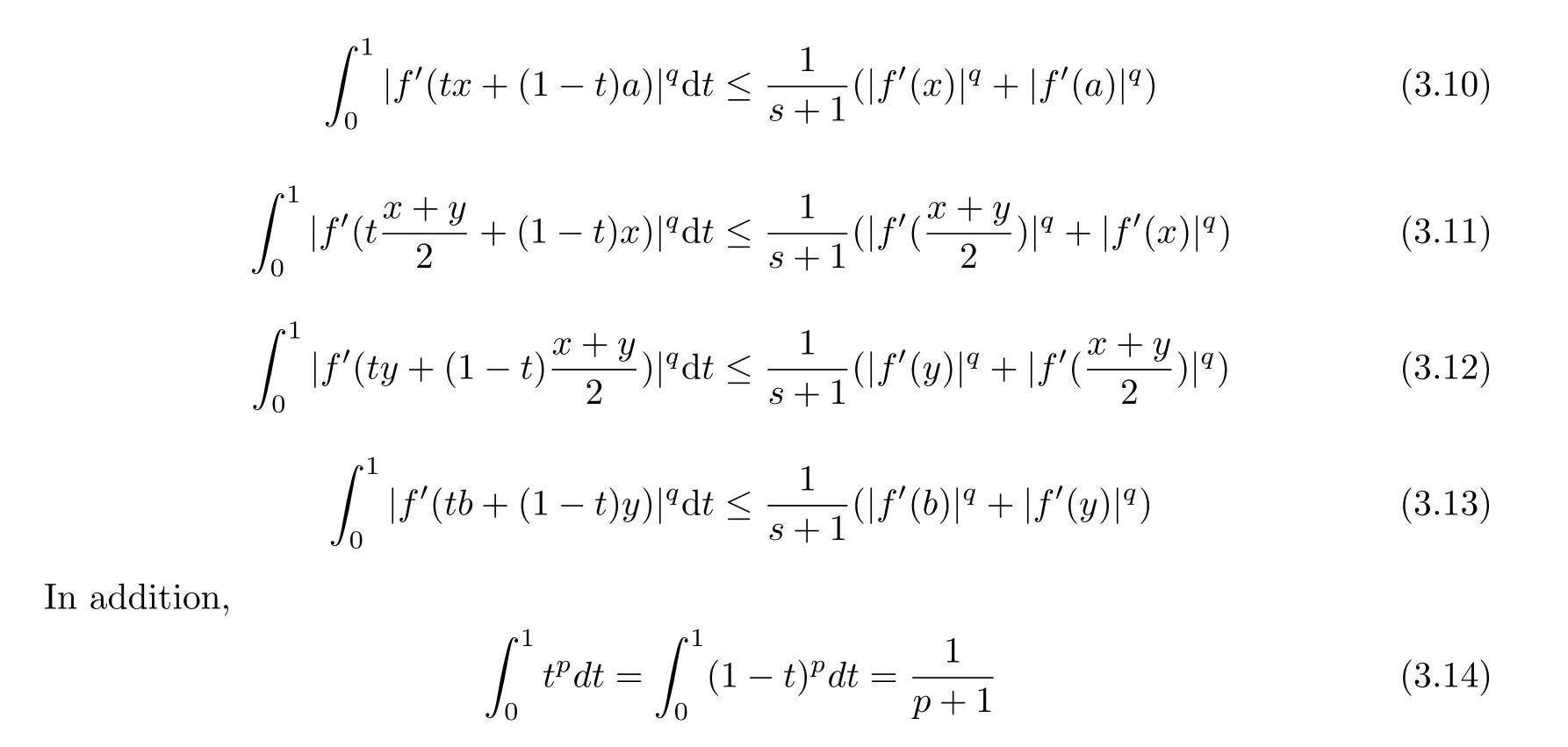
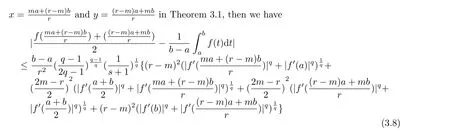

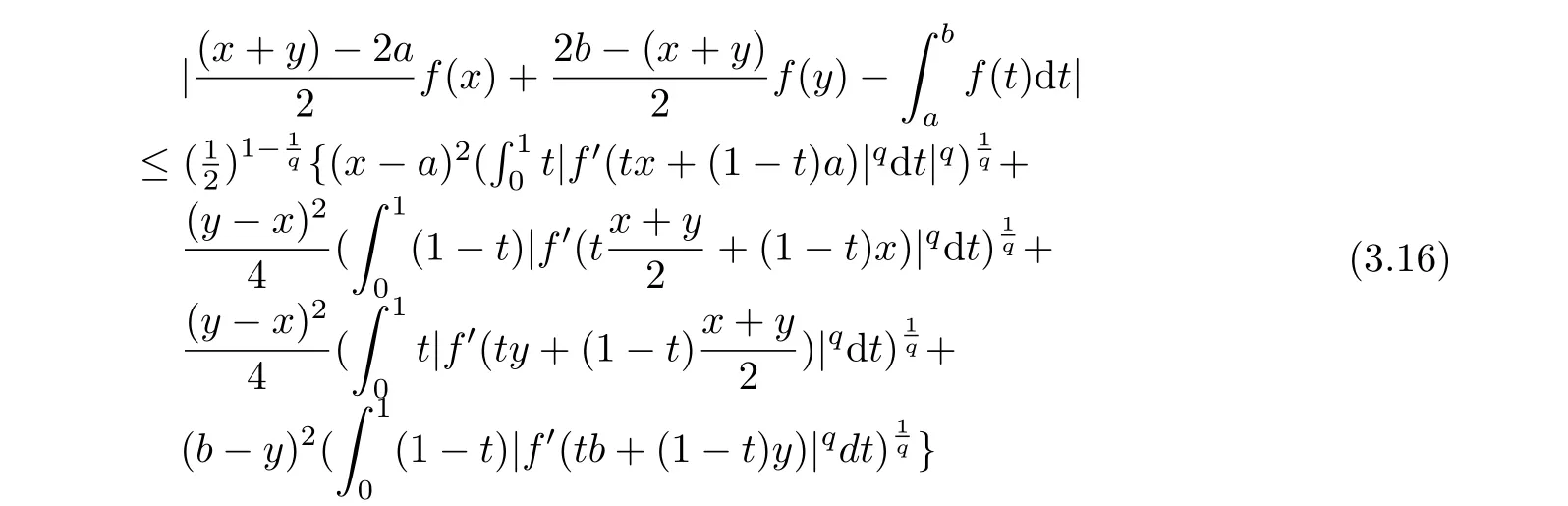
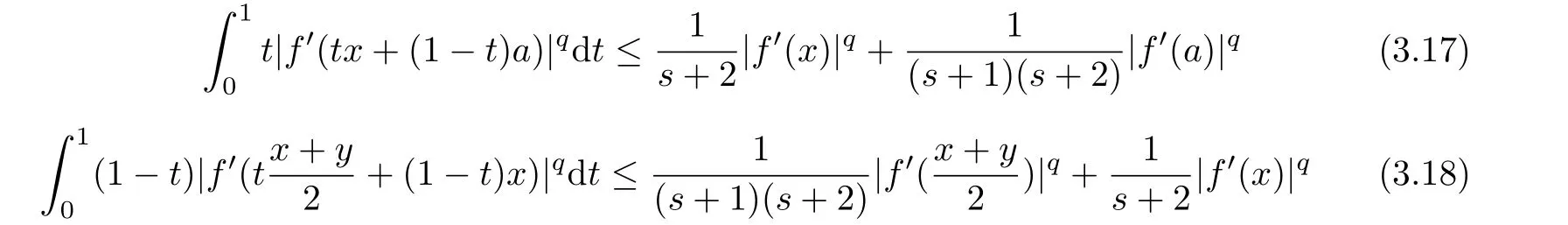
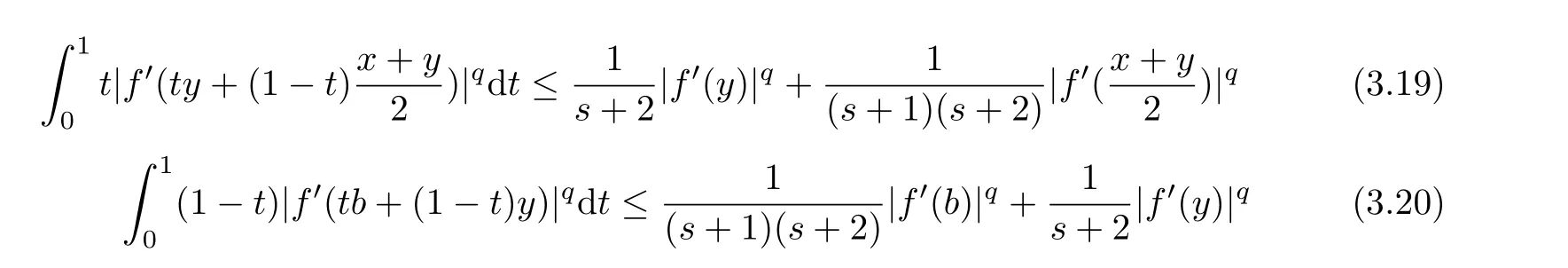

 Chinese Quarterly Journal of Mathematics2018年3期
Chinese Quarterly Journal of Mathematics2018年3期
