WEIGHTED NORM INEQUALITIES FOR ANISOTROPIC FRACTIONAL INTEGRAL OPERATORS
SUN Rui-rui,LI Jin-xia,LI Bao-de
(College of Mathematics and System Science,Xinjiang University,Urumqi 830046,China)
Abstract:Let A be an expansive dilation,α ∈ (0,1),p:=1/α and function v satisfy the anisotropic Muckenhoupt condition Ap,∞(A).In this paper,we study the boundedness of anisotropic fractional integral operators.By L(p, ∞)H?lder’s inequality and the σ-subaddictive property of∥ ·∥p′,1,we obtain some weighted norm inequalities for anisotropic fractional integral operators associated with the weight vp,which are anisotropic extension of Muckenhoupt and Wheeden[6].
Keywords:anisotropic;Muckenhoupt weight;fractional integral operator;BMO space
1 Introduction
Anisotropy is a common attribute of nature,which shows different characterizations in different directions of all or part of the physical or chemical properties of an object.For example,the elastic modulus,hardness or fracture strength of a crystal is different in different directions,which shows the anisotropic property of the crystal.The anisotropic property,in mathematics,can be expressed by a general discrete group of dilations{Ak:k∈Z},where A is a real n × n matrix with all its eigenvalues λ satisfying|λ|>1,which was first introduced by Bownik[1]and who further introduced the anisotropic Hardy spaces[2].We point out that such spaces include the classical isotropic Hardy spaces of Fe ff erman-Stein[3],the parabolic Hardy spaces of Calderón-Torchinsky[4,5],and still maintain the main properties of the corresponding classical Hardy spaces.
Fractional integrals played an important role in harmonic analysis and other fields,such as PDE(see[6,7]).Many scholars devoted to research the properties of fractional integrals(for example,see[8–10]).The celebrated result of fractional integrals is the Hardy-Littlewood-Sobolev inequality(see[11]).Hardy and Littlewood[12]proved that when n=1,fractional integral operator is bounded from Lp(R)to Lq(R),where α ∈ (0,1),p ∈ (1,∞)and q:=(1/p?α)?1,and Sobolev[13]obtained that for general n this result also holds true.The weighted(Lp(Rn),Lq(Rn))-boundedness of fractional integral operator was established by Muckenhoupt and Wheeden[6],where α ∈ (0,n),p ∈ (1,n/α)and q:=(1/p? α/n)?1.Ding and Lan[14]introduced the anisotropic fractional integral operator and Lan et al.[15]generalized the result of Muckenhoupt and Wheeden[6]to the anisotropic settings except the case q=∞.
Motivated by[1,6,15],we generalize the result of Muckenhoupt and Wheeden when q=∞[6,Theorems 7 and 8](see Theorem 2.8 below).It is worth pointing out that any Schwartz function is an anisotropic fractional integral kernel(see Remark 2.6(ii)(b)below).Moreover,we also obtain that if v?1is locally bounded,then Tαis bounded from Lp,∞vp(Rn)to the anisotropic bounded mean oscillation function space BMO(A)(see Theorem 2.10 below),which is probably new even for classical fractional integral operator of Sobolev[13].
This article is organized as follows.
In Section 2,we recall some notations and definitions concerning expansive dilations,anisotropic Muckenhoupt condition Ap,q(A),anisotropic fractional integral operator and BMO(A)space and state the main results,the proofs of which are given in Section 3.
Finally,we make some conventions on notations.Let Z+:={1,2,···}and N:={0} ∪Z+.Throughout the whole paper,we denote by C a positive constant which is independent of the main parameters,but it may vary from line to line.The symbol D.F means that D≤CF.If D.F and F.D,we then write D~F.If there are no special instructions,any space X(Rn)is simply denoted by X.For example,Lp(Rn)is simply denoted by Lp.For sets E,F ? Rn,we use E{to denote the set RnE,χEits characteristic function and E+F the algebraic sum{x+y:x∈E,y∈F}.For any index q∈[1,∞],we denote by q′its conjugate index,namely,1/q+1/q′=1.
2 Notion and Main Results
First we recall the notion of expansive dilatio ns on Rn,see[1,p.5].A real n×n matrix A is called an expansive dilation,shortly a dilation,if>1,where σ(A)denotes the set of all eigenvalues of A.Let λ?and λ+be two positive numbers such that
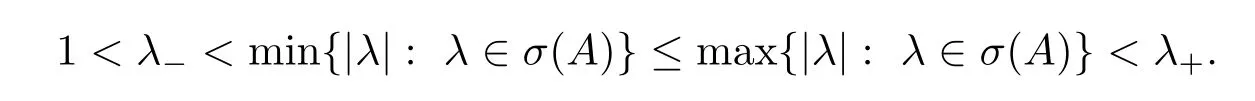
In the case when A is diagonalizable over C,we can even take
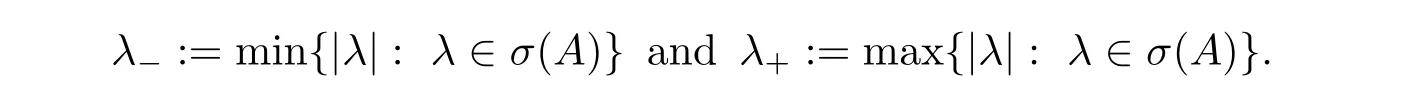
Otherwise,we need to choose them sufficiently close to these equalities according to what we need in our arguments.
It was proved in[1,p.5,Lemma 2.2]that,for a given dilation A,there exist a number r∈(1,∞)and a set?:={x∈Rn:|Px|<1},where P is some non-degenerate n×n matrix,such that? ? r? ? A?,and by a scailing,one can additionally assume that|?|=1,where|?|denotes the n-dimensional Lebesgue measure of the set?.Let Bk:=Ak? for k∈Z.Then Bkis open,convex,Bk?rBk?Bk+1and|Bk|=bk,here and hereafter,b:=|detA|.Throughout the whole paper,let σ be the minimum positive integer such that 2B0?AσB0=Bσ.Then,for all k,j∈Z with k≤j,it holds true that

Definition 2.1 A quasi-norm,associated with an expansive matrix A,is a Borel measurable mapping ρA:Rn→ [0,∞),for simplicity,denoted by ρ,satisfying
(i) ρ(x)>0 for all x ∈ Rn{0n},here and hereafter,0n:=(0,···,0);
(ii) ρ(Ax)=bρ(x)for all x ∈ Rn,where,as above,b:=|detA|;
(iii) ρ(x+y)≤ H[ρ(x)+ρ(y)]for all x,y ∈ Rn,where H ∈ [1,∞)is a constant independent of x and y.
In the standard dyadic case A:=2In×n,ρ(x):=|x|nfor all x ∈ Rnis an example of quasi-norms associated with A,here and hereafter,|·|always denotes the Euclidean norm in Rn.
It was proved in[1,p.6,Lemma 2.4]that all quasi-norms associated with a given dilation A are equivalent.Therefore,for a given expansive dilation A,in what follows,for simplicity,we always use the step quasi-norm ρ defined by setting,for all x ∈ Rn,
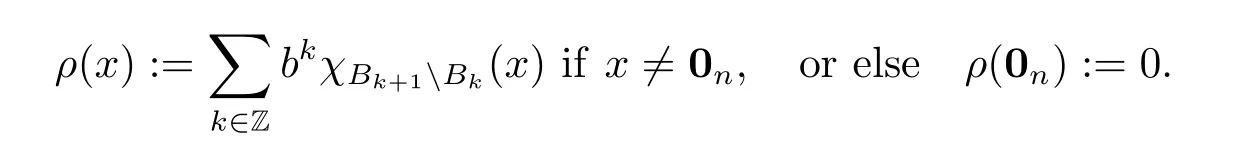
By(2.1)and(2.2),we know that,for all x,y∈Rn,
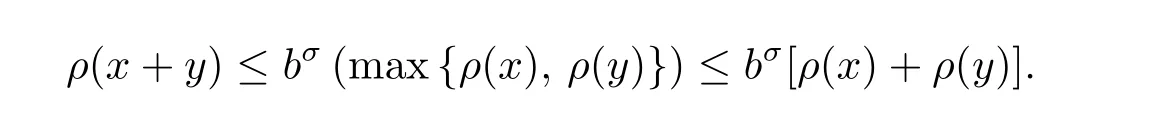
Moreover,(Rn,ρ,dx)is a space of homogeneous type in the sense of Coifman and Weiss[16,17],where dx denotes the n-dimensional Lebesgue measure.
In what follows,for convenience,we always define
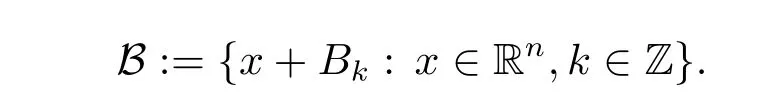
Definition 2.2 Let
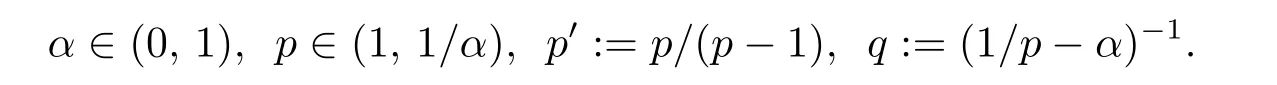
A function v:Rn→[0,∞)is said to satisfy the anisotropic Muckenhoupt condition Ap,q(A),denoted by v∈Ap,q(A),if there exists a positive constant C such that,for any B∈B,
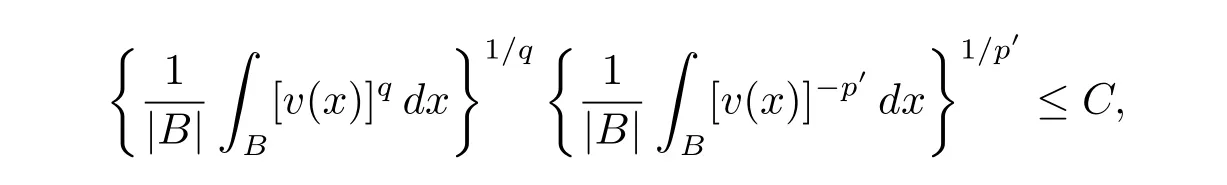
and when q=∞,
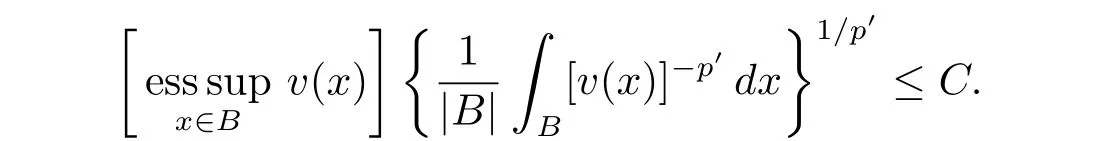
Definition 2.3 Let p∈ (0,∞]and ω :Rn→ [0,∞)be a measurable function.The weighted Lebesgue spaceis defined to be the space of all measurable functions f such that
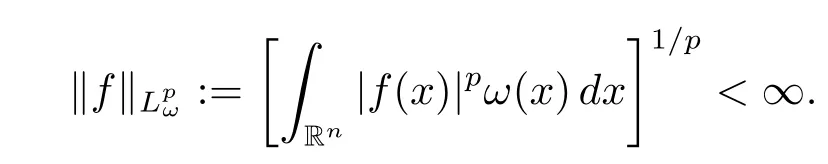
The weighted weak Lebesgue spaceis defined to be the space of all measurable functions f such that
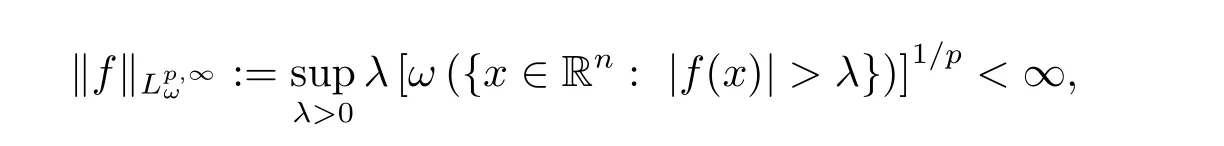
Denote the space of all Schwartz functions on Rnby S,namely,the set of all C∞functions ? satisfying that,for any α ∈ Nnand any ?∈ N,
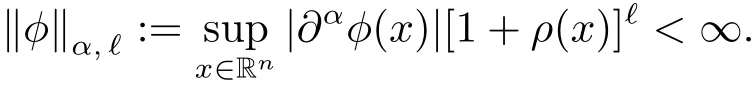
The dual space of S,namely,the space of all tempered distributions,equipped with the weak-? topology,is denoted by S′.
Remark 2.4 By[1,p.11,Lemma 3.2],we know that the Schwartz function space S,equipped with the pseudo-norms{∥ ·∥α,?}α∈Nn,?∈N,is equivalent to the classical Schwartz function space,equipped with the pseudo-normswhere,for any α ∈ Nn,?∈ N and any ? ∈ S,
Now we recall the definition of anisotropic fractional integral operators associated with a quasi-norm ρ,which comes from[15].
Definition 2.5 Let α ∈ (0,1).A locally integrable function K on ? :={(x,y) ∈Rn×Rn:x ≠y}is said to be an anisotropic fractional integrable kernel(with respect to a dilation A and a quasi-norm ρ)if there exist positive constants C and γ such that

We call that Tαis an anisotropic fractional integrable operator if Tαis a continuous linear operator maps S into S′and there exists an anisotropic fractional integrable kernel K such that,for all f∈and x?suppf,
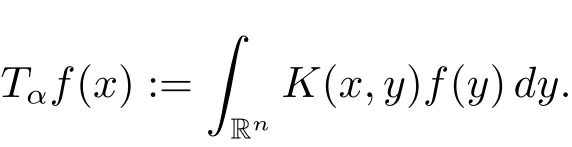
In particular,if K(x,y):=[ρ(x ? y)]?1+αwith(x,y) ∈ ? and α ∈ (0,1),we denote the corresponding fractional integral operator by.
Remark 2.6 (i)If K(x,y)=1/|x?y|n?αwith(x,y)∈ ? and α ∈ (0,n),then Tαis reduced to the classical fractional integral operator[12]for the one dimensional case and[13]for the n dimensional case.
(ii)If Tαis a fractional integral operator with convolutional kernel K(x)on Rn{0n},then the above conditions(ii)and(iii)are reduced to
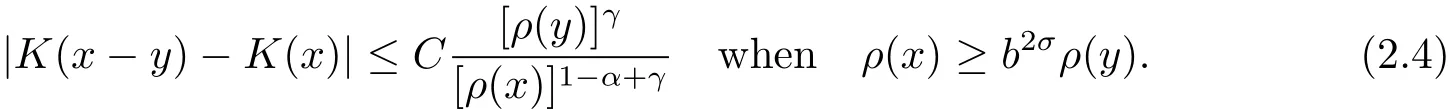
We give three examples for this case.
(a)if α ∈ (0,n),ρ(x):=|x|nand K(x):=1/|x|n?αwith x ∈ Rn{0n},then K(x)is a convolutional kernel.Moreover,Lan[15,p.4]pointed out that,for any x∈Rn{0n}and α ∈ (0,1),K(x):=[ρ(x)]?1+αis also a convolutional kernel,or see[18,Lemma 2.3]for more details.
(b)if K ∈S,then the operator Tα:S → S′with such convolutional kernel K on Rn{0n}is a fractional integral operator with α ∈ (0,1)and γ ∈ (0,logb(λ?)].In fact,Definition 2.5(i)is obvious,we just need to prove(2.4)with α ∈ (0,1)and γ ∈ (0,logb(λ?)].There exist some l∈ Z and m ∈ N such that ρ(y)=bland ρ(x)=bl+m+2σ.By the mean value theorem,we have
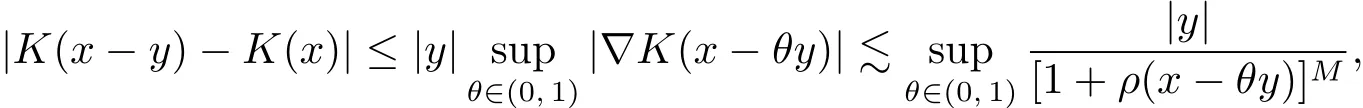
where M ∈ (0,∞)to be fixed later.If l≤ 0,for x ∈ (Bl+m+2σ){and θy ∈ Bl+1(since y∈Bl+1and Bl+1is convex),by σ>1,m≥0 and(2.2),we obtain
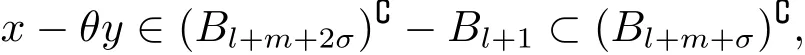
which implies that

From this,|y|.[ρ(y)]logb(λ?)when ρ(y)≤ 1(see[1,p.11,Lemma 3.2])and m ∈ N,it follows that,for any γ ∈ (0,logb(λ?)]and by choosing M=1 ? α +logb(λ?),
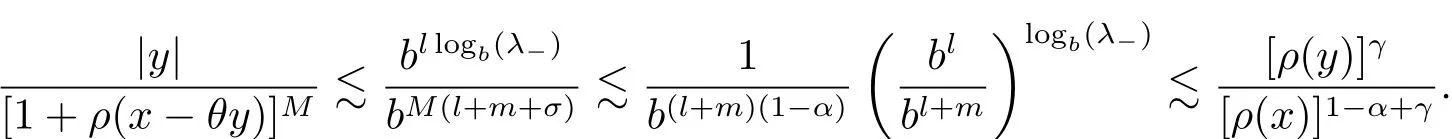
If l>0,by(2.5),|y|.[ρ(y)]logb(λ+)when ρ(y)>1(see[1,p.11.Lemma 3.2]),m ∈ N and logb(λ+) ≥ logb(λ?),we see that,for any γ ∈ (0,logb(λ?)]and by choosing M=1?α +logb(λ+),
Definition 2.7 A locally integrable function b is said to be in anisotropic bounded mean oscillation function space BMO(A)if
The main results of this article are the following two theorems,the proofs of which are given in Section 3.
Theorem 2.8 Let α ∈ (0,1),p:=1/α and v(x)be a nonnegative function on Rn.If v∈Ap,∞(A),then there exists a positive constant C such that,for every B ∈B,
In particular,when Tα=satis fies(2.6)if and only if v∈Ap,∞(A).
Remark 2.9 Lan[15,Theorems 1.3 and 1.4]obtained the weighted boundedness of anisotropic fractional singular integral operator associated with Ap,q(A),where q<∞.The above Theorem 2.8 considers the case q=∞,which is also an anisotropic extension of Muckenhoupt and Wheeden[6,Theorems 7 and 8].
Theorem 2.10 Let α ∈ (0,1),p:=1/α and v(x)be a nonnegative function on Rn.If v?1is locally bounded,then Tαis bounded fromto BMO(A).
3 Proofs of Theorems 2.8 and 2.10
Proof of Theorem 2.8 Let α∈(0,1).Fix a dilated ball B:=x0+Bj∈B with some x0∈ Rnand j∈ Z,and B?:=x0+Bj+4σ.Then

and
To prove(2.6)holds true,it is sufficient to prove
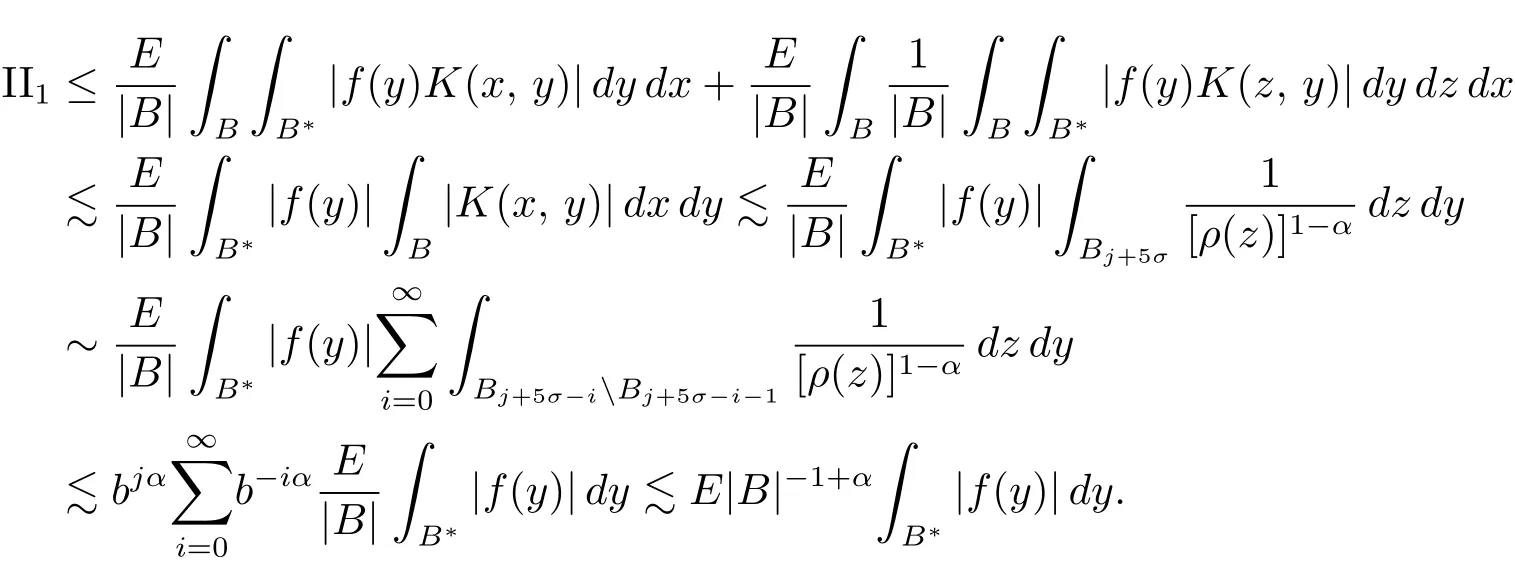
By p=1/α,1/p′=1 ? α,L(p,∞)H?lder’s inequality(see[19,p.262]),(see[19,(2.2)]),the proof of which is identity to that of[6,Lemma 2],and v ∈ Ap,∞(A),we see that
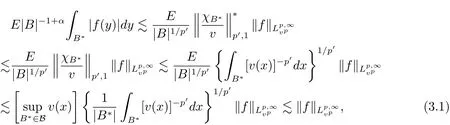
By(2.1)and(2.2)with x,z∈ B and y∈ (B?){,we see that x?z∈ Bj+σand x ? y ∈ (Bj+3σ){,which implies that ρ(x ? z) By ρ(x ? y)≥ bj+3σand ρ(x0? x) From this,L(p,∞)H?lder’s inequality(see[19,p.262])and the fact(see[19,(2.2)]),it follows that Then in order to obtain II2. ∥f∥Lpv,p∞,it suffices to show that where the implicit constant is independent of B. Finally,it remains to prove that if Tα=as in Definition 2.5 satis fies(2.6),then v∈ Ap,∞(A).To prove this,we first show that there exists a constant k0∈ Z+such that,for every B:=x0+Bj∈B and every y∈B, By(2.1)with x,y∈B,we have x?y∈Bj+σ,which implies that Then we have Therefore,from this and(3.5),it follows that Since α∈(0,1),by choosing k0sufficiently large,we see that and hence(3.4)holds true. Now fix a ball B∈B and let f be a nonnegative integrable function with suppf?B and k0being as in(3.4).Then,by Fubini’s theorem and(3.4),we have Therefore,by Minkowski’s inequality,(2.6)and suppf ? B,we see that namely, Then combining(3.8)and(3.7)with f(x)=[v(x)]?p′χB(x),we have which,together with p(p′? 1)=p′,implies that and hence v ∈ Ap,∞(A). which is desired.Then and hence which implies that v∈ Ap,∞(A).This finishes the proof of Theorem 2.8. Proof of Theorem 2.10 The proof of Theorem 2.10 is similar to that of Theorem 2.8.So we use the same notations as in the proof of Theorem 2.8.Since Then,when v?1is locally bounded,we only need to prove that,for any B ∈ B,and For II,by(3.2),(3.3),γ ∈ (0,∞)and,we see that which,together with(3.9),completes the proof of Theorem 2.10.
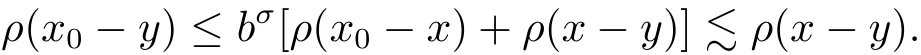

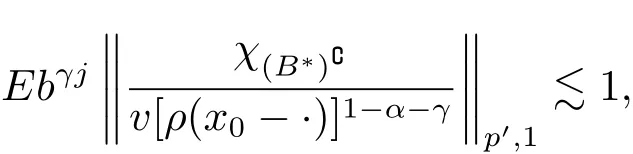
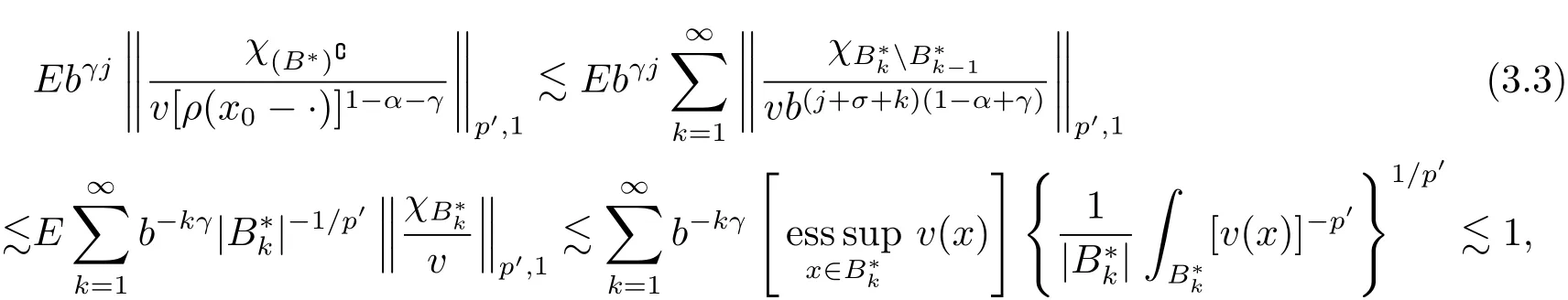
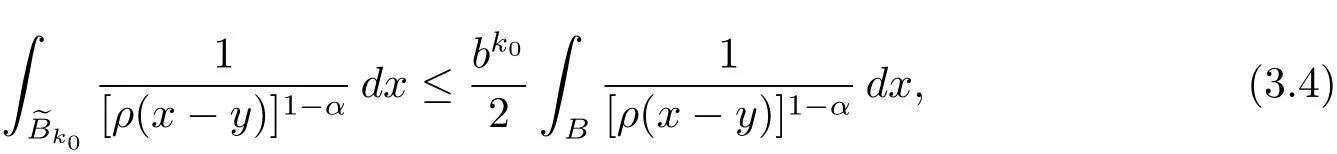


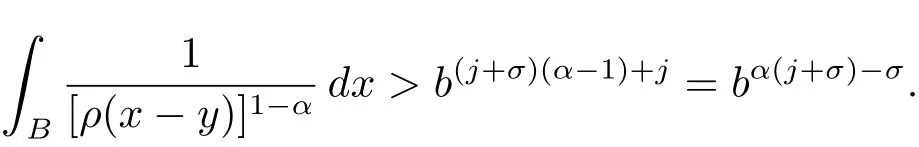
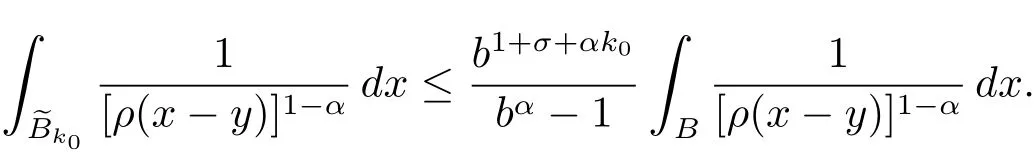
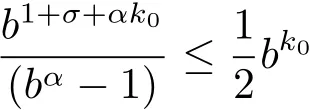
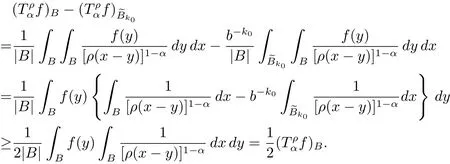
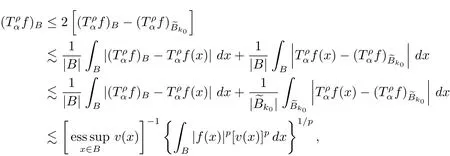
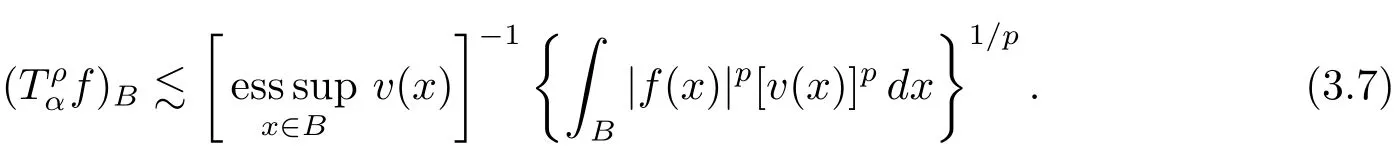
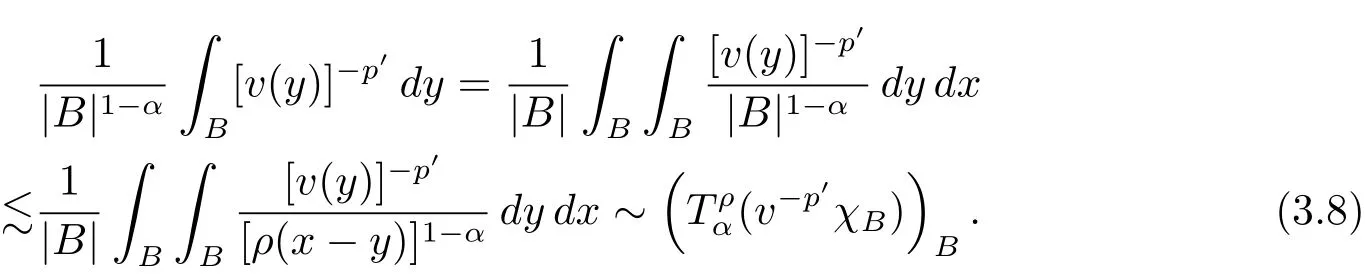
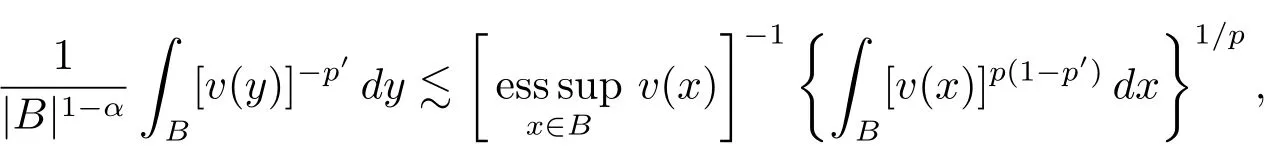
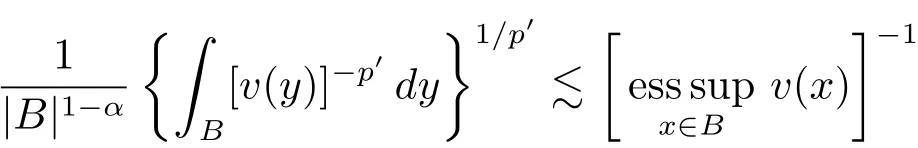
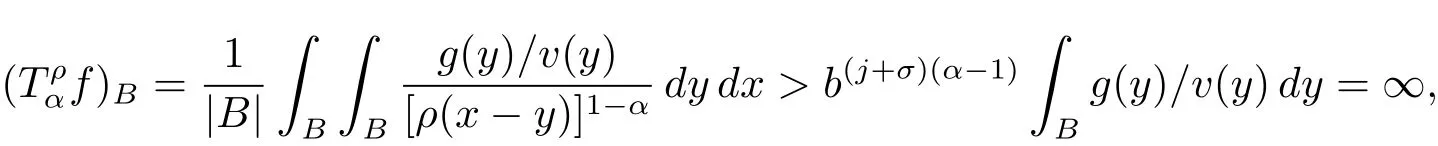

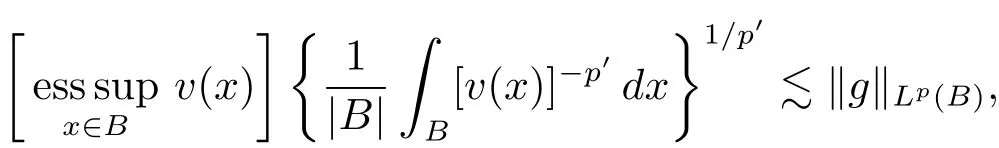
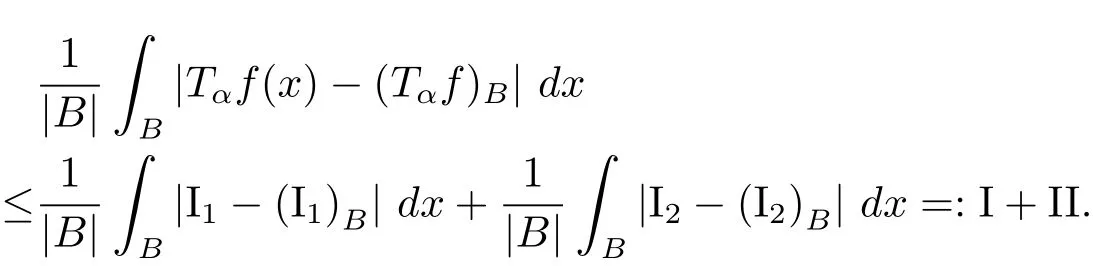

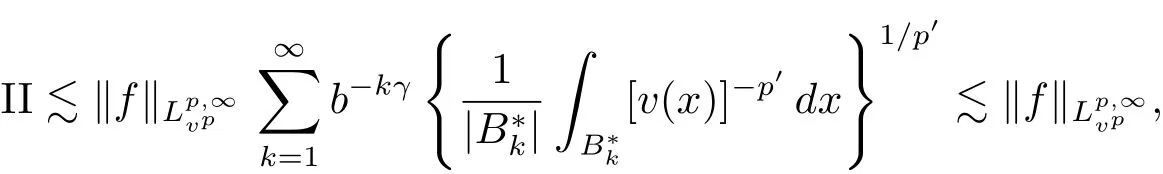
- 數(shù)學(xué)雜志的其它文章
- RELATIONSHIPS BETWEEN VECTOR VARIATIONAL-LIKE INEQUALITIES AND MULTI-OBJECTIVE PROGRAMMING INVOLVING GENERALIZED ARCWISE CONNECTED FUNCTIONS
- NABLA-HUKUHARA DERIVATIVE OF FUZZY-VALUED FUNCTIONS ON TIME SCALES
- FROM LEIBNIZ SUPERALGEBRAS TO LIE-YAMAGUTI SUPERALGEBRAS
- ON THE UNIT GROUPS OF THE QUOTIENT RINGS OF IMAGINARY QUADRATIC NUMBER RINGS
- THE APPLICATION OF THE SECOND KIND CHEBYSHEV WAVELETS FOR SOLVING HIGH-ODER MULTI-POINT BOUNDARY VALUE PROBLEMS
- ON THE LOCAL WELL-POSEDNESS FOR THE KDVKS EQUATION

