ON THE LOCAL WELL-POSEDNESS FOR THE KDVKS EQUATION
WANG Hong-wei,ZHANG Yuan-yuan
(1.School of Mathematics and Statistics,Anyang Normal University,Anyang 455000,China)
(2.Teaching and Research Department of Mathematics,Kaifeng University,Kaifeng 475000,China)
Abstract:In this paper,we consider the Cauchy problem for the KdVKS equation ut+=0.By means of the[k;Z]multiplier norm method of Tao,we prove the associated initial value problem is locally well-posed in Sobolev spaces Hs(R)for s>?1,which improves the conclusions drawn by Biagioni et al.
Keywords:KdVKS equation;local well-posedness;Cauchy problem
1 Introduction
The purpose of this work is to study the local well-posedness for the Cauchy problem associated to the Korteweg-de Vries Kuramoto-Sivashinsky equation
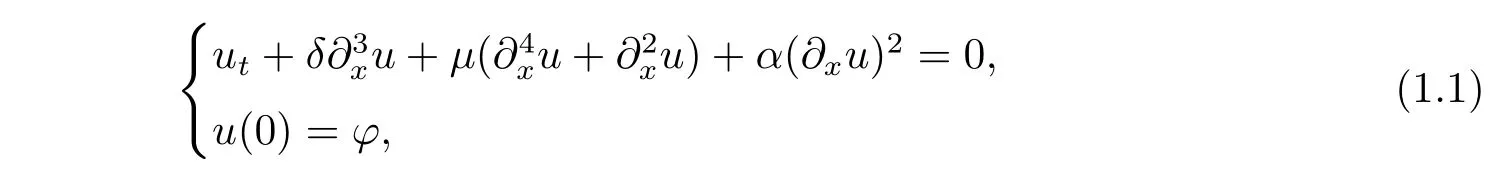
where x ∈ R,t ∈ R+,u is a real-valued function and δ,μ and α are constants such thatμ >0, δ≠0 and α ≠0.The KdV-KS equation arises in interesting physical situations,for example as a model for long waves on a viscous fluid flowing down an inclined plane[2]and for deriving drift waves in a plasma[3].
In[1],using the dissipative e ff ect of the linear part,Biagioni,Bona,Iorio and Scialom showed that the Cauchy problem associated to(1.1)is globally well-posed in Hs(R)(s>1).They also proved that the solutions of the KdV-KS equation converge to the solutions of the Kuramoto-Sivashinsky equation when the dispersive parameter δ goes to zero.The generalization of KdVKS equation is the following dispersive-dissipative equation
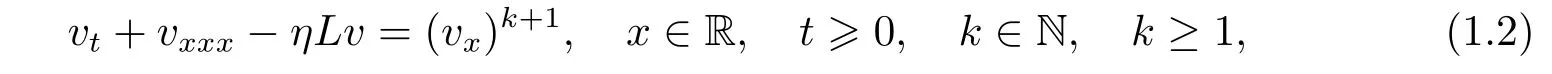
where the linear operator L is defined via the Fourier transform bycLf(ξ)= ?Φ(ξ)df(ξ).The Fourier symbol Φ(ξ)is of the form

where p ∈ R+and|Φ(ξ)|6 C(1+|ξ|q)with 0 6 q Before presenting the precise statement of our main result,we give the definition of the working space of this paper.Without loss of generality,we will suppose that δ=μ=α=1 in the rest of this paper. Definition 1.1 For s,b∈R,we have that Xs,bdenotes the completion of the Schwartz functions with respect to the norm As a consequence of this definition,we immediately have for b>1/2,that Xs,bis embedded in C(R;Hs(R)). In sequel,we state the main results of this work. Theorem 1.1 Let s> ?1 and φ ∈ Hs(R).Then there exist b=b(s)∈ (1/2,1)and T=T(∥φ∥Hs(R))>0 such that the Cauchy problem(1.1)has a unique solution u(t)on[0,T]satis fies u∈C([0,T];Hs(R))∩.Moreover,the map solution is smooth. For any positive number x and y,the notation x.y means that there exists a positive constant c such that x 6 cy;and we denote x~y when x.y and y.x.We shall denote by?f the Fourier transform of f. Now we consider the initial value problem associated to the linear parts of(1.1), The unique solution of(2.1)is given by the semigroup V(t)defined as follows By Duhamel’s principle,the solution of(2.1)is equivalent to Actually,to prove the local existence result,we shall apply a fixed point argument to the following truncated version of(2.3) where t∈ R and θ is a time cuto fffunction satisfying and denote for given T>0,θT(·)= θ(·/T).Indeed,if u solves(2.4)then u is a solution of(2.3)on[0,T]. Here are some fundamental estimates for the operator V(t).Since the proofs of these estimates are standard,we omit the proofs.The reader can find some similar results for other similar operators from[8]. Lemma 2.1(Homogeneous linear estimate)Let s∈R, Lemma 2.2 (Non-homogeneous linear estimate)Let s∈R,there exists C>0 such that,for any f ∈ Xs,b?1, In this section,we derive the crucial trilinear estimate to prove the local existence result from Tao’s multiplier norm estimate for KdV equation[4]. Let Z be any abelian additive group with an invariant measure dξ.For any integer k>2,let Γk(Z)denote the hyperplane endowed with the measure Following Tao[4],we define a[k;Z]-multiplier to be a function m:Γk(Z)→ C.The multiplier norm ∥m∥[k;Z]is the best constant such that holds for all test functions fion Z. Meanwhile,we need to review some of Tao’s notations.Any summations over capitalized variables such as Ni,Li,H are presumed to be dyadic.Let N1,N2,N3>0,it will be convenient to define the quantities Nmax>Nmed>Nminto be the maximum,median,and minimum of N1,N2,N3respectively.Likewise,we have Lmax>Lmed>Lminwhenever L1,L2,L3>0.We adopt the following summation convention.Any summation of the form Lmax~ ···is a sum over the three dyadic variables L1,L2,L3&1,thus for instance Similarly,any summation of the form Nmax~ ···sum over the three dyadic variables N1,N2,N3>0,thus for instance If τ,ξ and h(ξ)are given with τ1+τ2+τ3=0,then we write λ := τ??(ξ).Similarly we have λi:= τi? ?(ξi).We refer to ? :Γ3(Z)→ R as the resonance function,which is defined by By the dyadic decomposition of each variable ξior λi,as well as the function h(ξ),we are led to consider where XN1,N2,N3;H;L1,L2,L3is the multiplier From the identities ξ1+ ξ2+ ξ3=0 and on the support of the multiplier,we see that χN1,N2,N3;H;L1,L2,L3vanishes unless and For the KdV group,where ?(ξ)= ξ3,from the resonance identity we may assume that since the multiplier in(3.3)vanishes otherwise. Lemma 3.1(see[4,Propositon 6.1])Let H,N1,N2,N3,L1,L2,L3>0 obey(3.5)–(3.7)and let the dispersion relations be given by(3.4). (i)If Nmax~Nminand Lmax~H,then we have (ii)If N2~N3?N1and H~L1&L2,L3,then Similarly for permutations. (iii)In all other cases,we have Proposition 3.1 For s>?1 and u,v∈Xs,b,there exists b∈(1/2,1)such that the bilinear inequality holds where the implicit constant depending only on s and b. ProofBy Plancherel’s formula and duality,it suffices to show that By the dyadic decomposition of the variables ξj,λj,h(ξ),j=1,2,3,we may assume that|ξj|~ Nj,|λj|~ Lj,|h(ξ)|~ H.Using the translation invariance of the[3;Z]-multiplier norm,we can always restrict our estimate on Lj&1 and max(N1,N2,N3)=N&1.The comparison principle and the orthogonality reduce the multiplier norm estimate(3.12)to showing that and for all N&1.Estimates(3.13)and(3.14)will be accomplished by means of the fundamental estimate Lemma 3.1 and some delicate summation. Fix N&1,this implies(3.7).We first prove(3.14).By(3.10),we reduce to By symmetry we only need to consider two cases:N1~N2~N,N3=Nminand N1~N3~N,N2=Nmin. (i)In the first case N1~N2~N,N3=Nmin,estimate(3.15)can be further reduced to then performing the L summations,we reduce to which is true if 2s+2>0.So(3.15)is true if s>?1. (ii)In the second case N1~N3~N,N2=Nmin,estimate(3.15)can be reduced to Before performing the L summations,we need pay a little more attention to the summation of Nmin.So we reduce to which is obviously true if s>?.So(3.15)is true if s>?. Now we show the low modulation case(3.15).We may assume Lmax~N2Nmin.We first deal with the contribution where(3.8)holds.In this case,we have N1,N2,N3~N&1,so we reduce to Now we deal with the cases where(3.9)applies.By symmetry we only need to consider two cases In the first case,we reduce by(3.9)to Performing the N3summation,we reduce to which holds if s>?1. In the second case,we simplify using(3.9)to Performing the L summation,we reduce to To finish the proof of(3.15),it remains to deal with the cases where(3.10)holds.This reduces to To estimate(3.18),by symmetry we need to consider two cases:N1~N2~N,N3=Nminand N1~N3~N,N2=Nmin. (i)If N1~N2~N,N3=Nmin,then estimate(3.18)can be further reduced to performing the L summations,we reduce to which is true if s>?1. (ii)If N1~N3~N,N2=Nmin,then the estimate(3.15)can be reduced to performing the L summations,we reduce to which is obviously true if s>. In this section,we will use the linear and nonlinear estimates to provide proofs of the local well-posedness results stated in Theorem 1.1. Proof of Theorem 1.1 Let s> ?1 and φ ∈ Hs(R).We prove the existence of a solution u of the integral formulation(2.3)on some interval[0,T]for T<1 small enough.Define We want to use the Picard fixed point theorem to find a solution of in the space Xs,b. Using(2.6),(2.7)and(3.11),we deduce that,there exists a constant C>0 such that Since the same computation leads to We define with M=2c∥φ∥Hs.Then if we choose T such that (4.3)and(4.4)imply that ΓTis a contraction map on the Banach space(M).Thus we deduce by the fixed point theorem that there exists a unique solution u∈(M)of(4.2).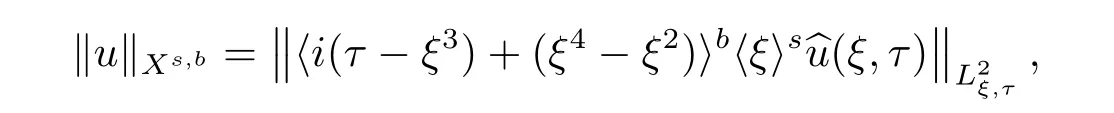
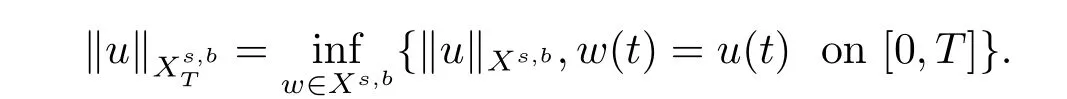
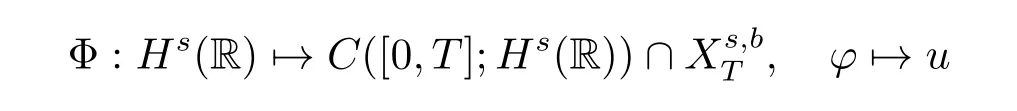
2 Notations and Preliminary Results

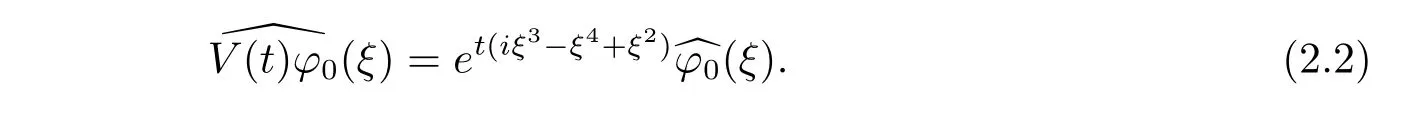
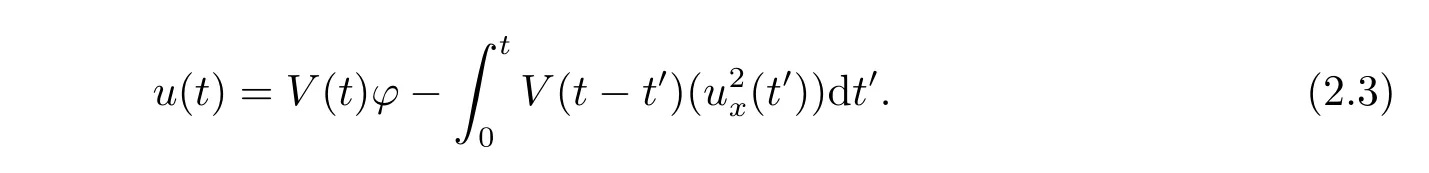
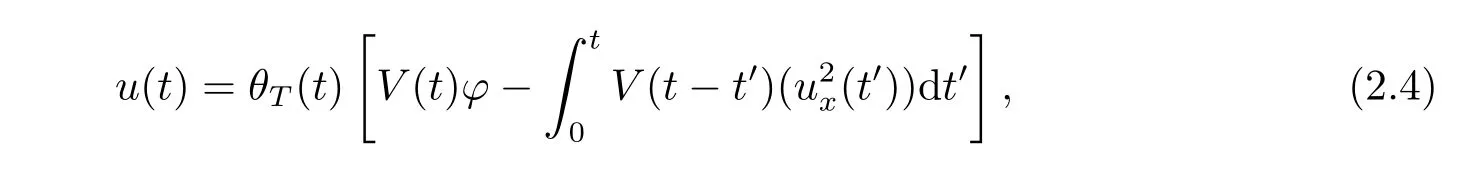
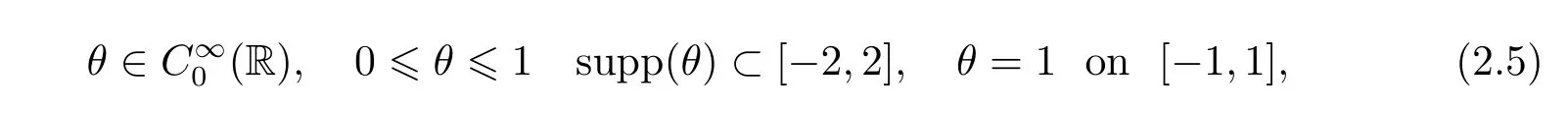
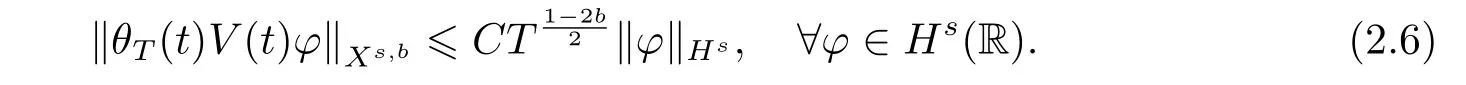

3 Binilear Estimate
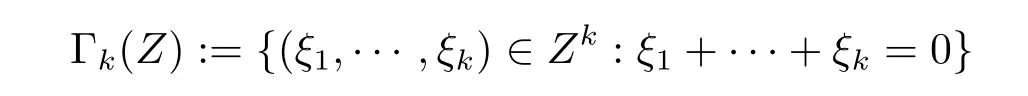
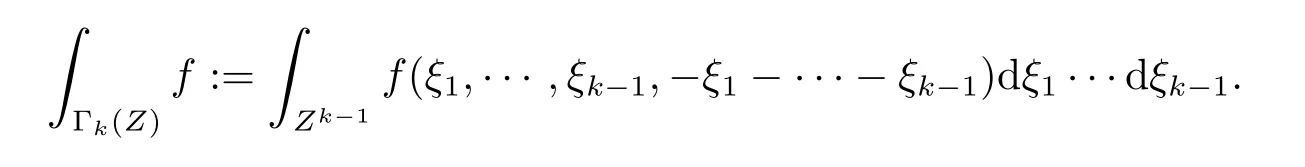
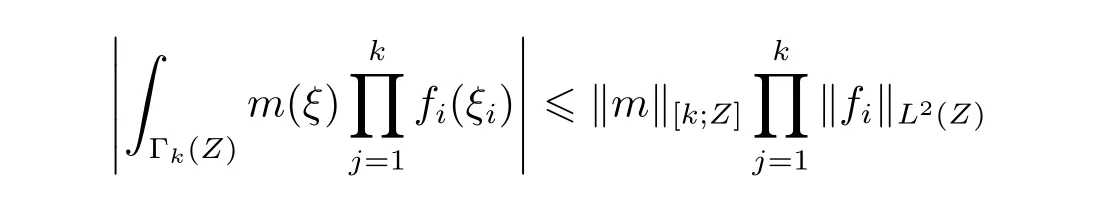
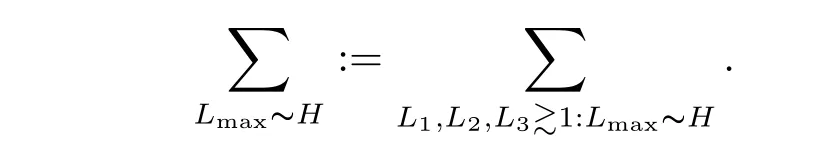
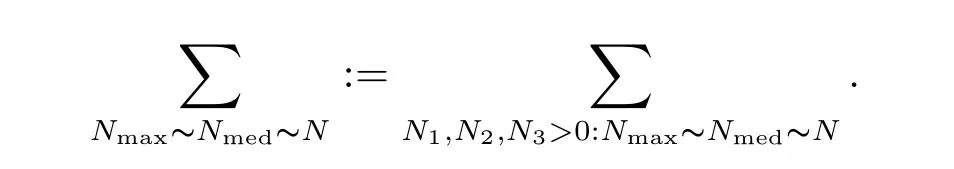
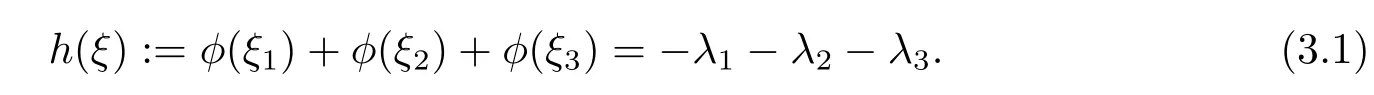
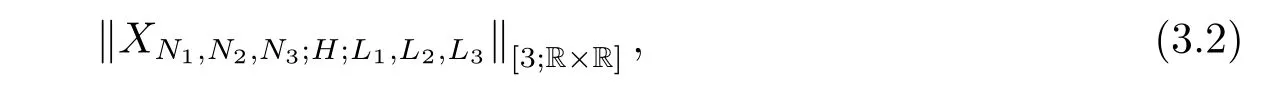
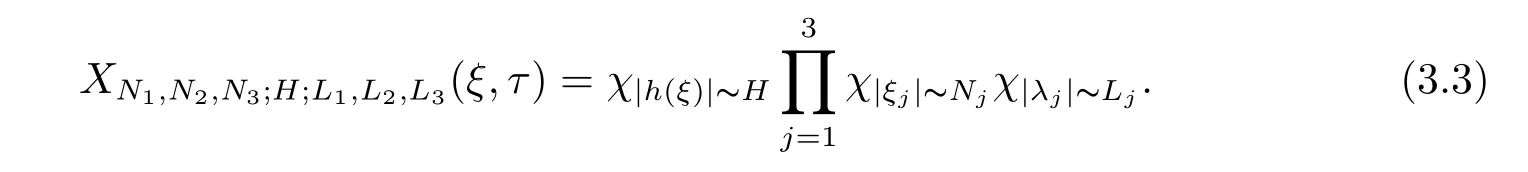


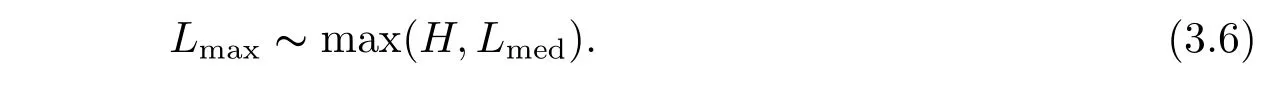
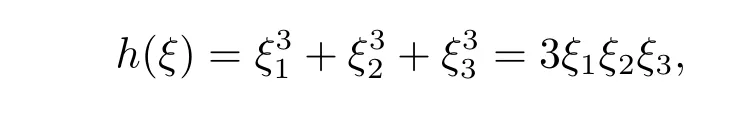


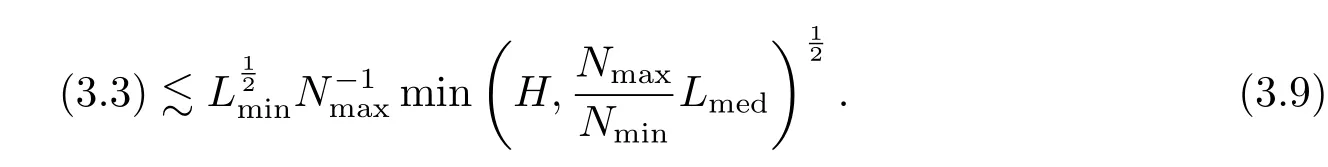
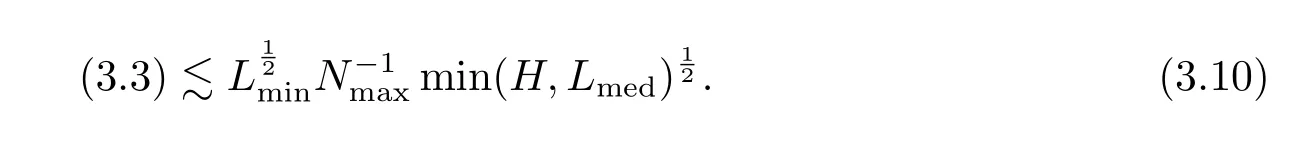
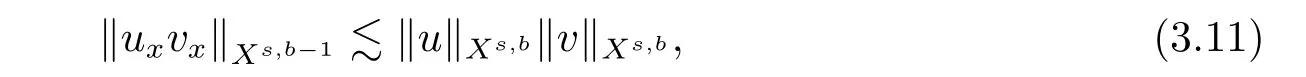
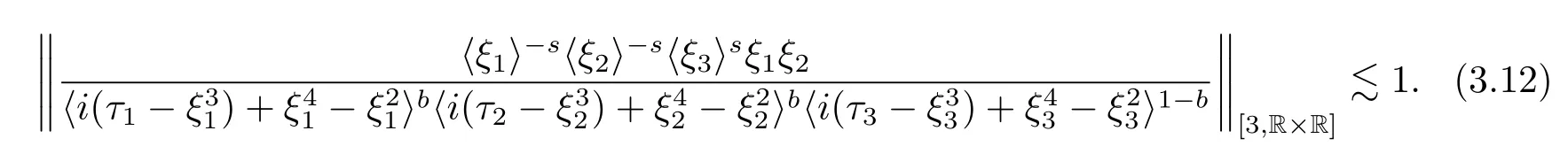
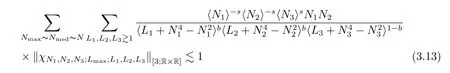
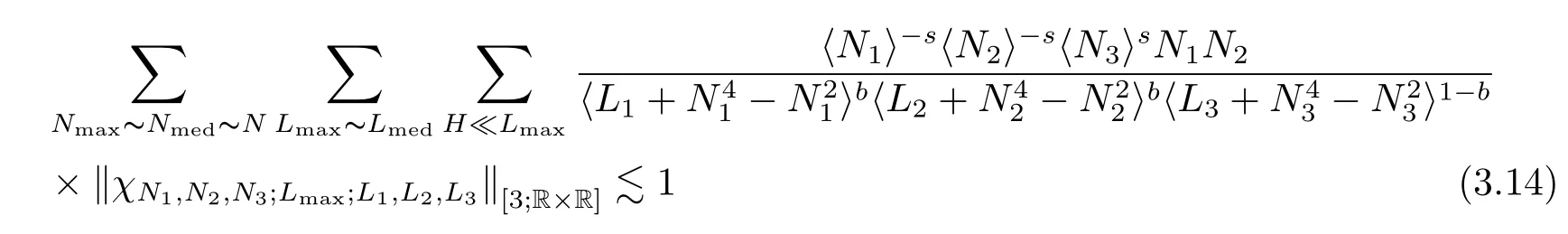
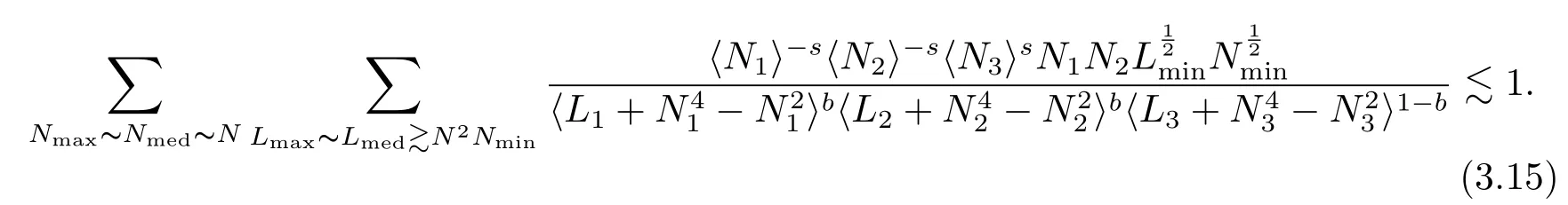
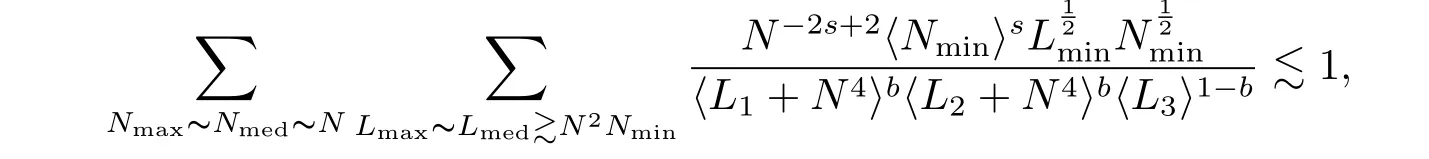
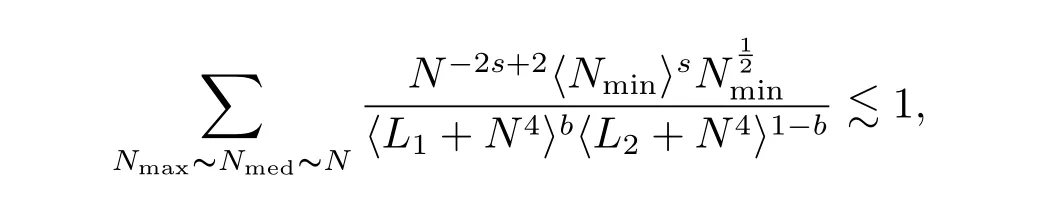
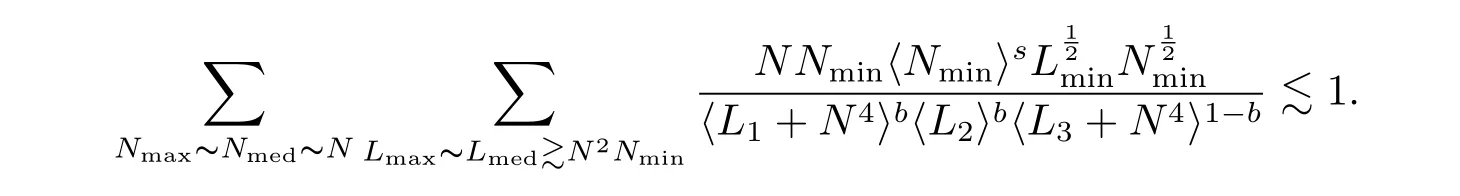
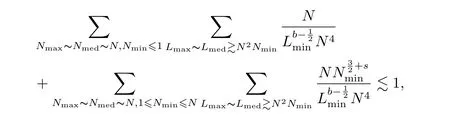
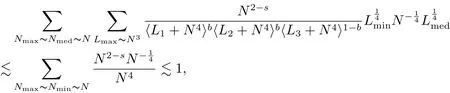
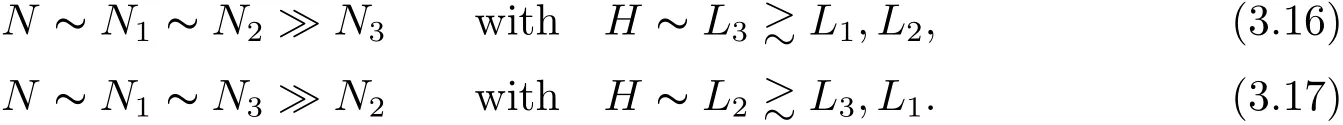
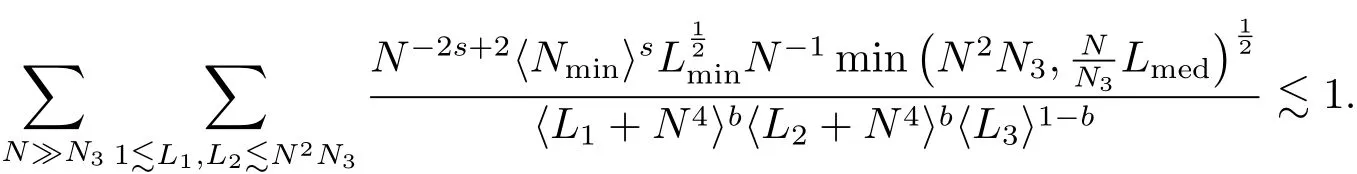
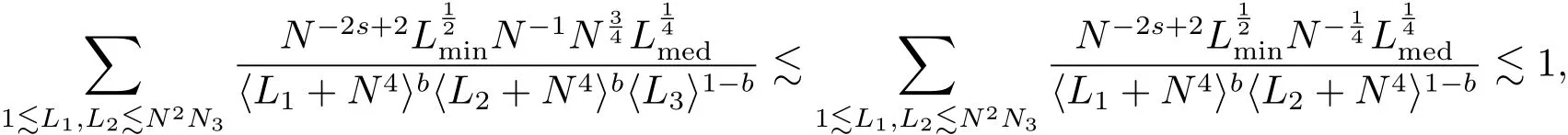

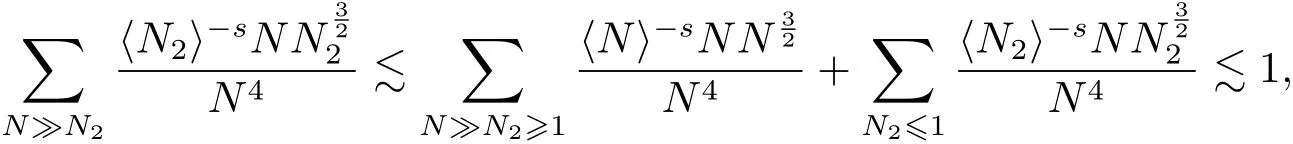
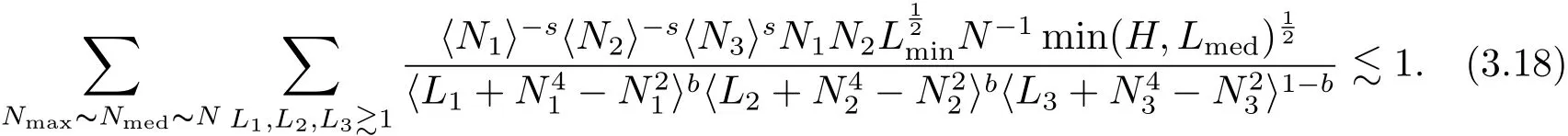
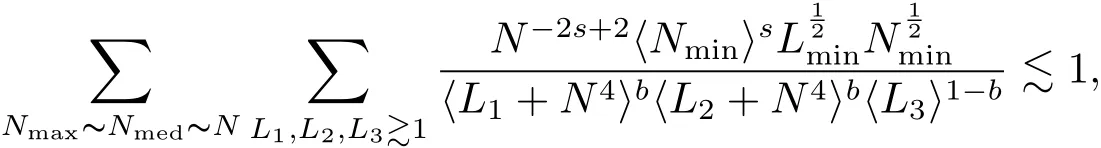
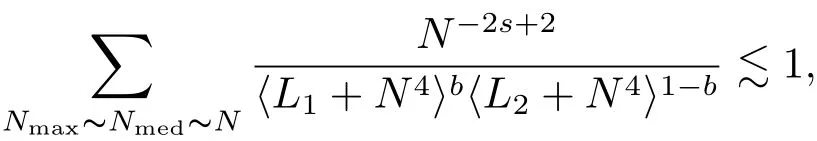
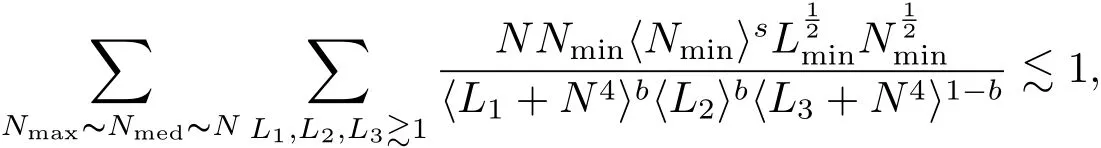
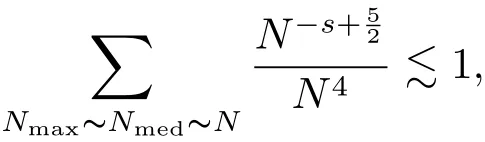
4 Proof of Main Result
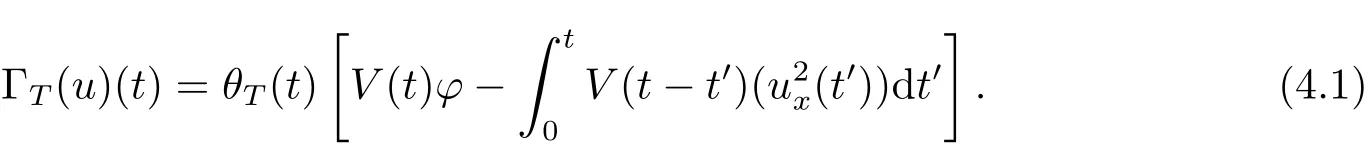

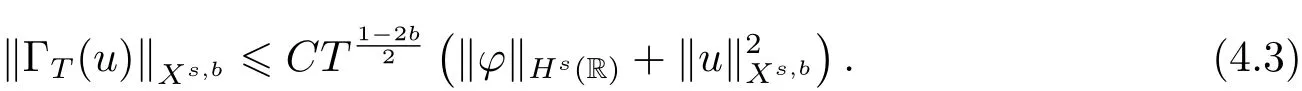
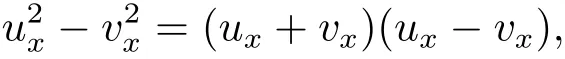
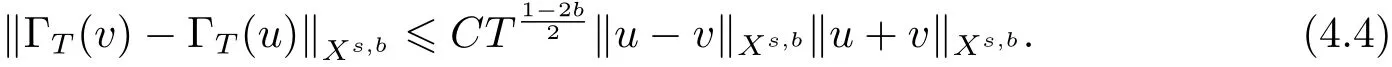
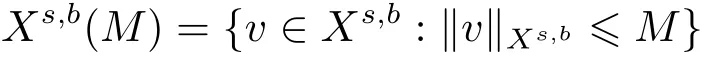
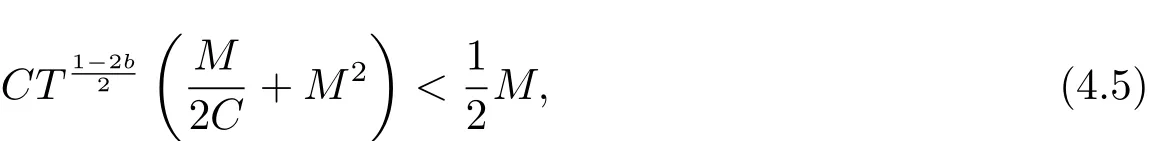
- 數(shù)學(xué)雜志的其它文章
- RELATIONSHIPS BETWEEN VECTOR VARIATIONAL-LIKE INEQUALITIES AND MULTI-OBJECTIVE PROGRAMMING INVOLVING GENERALIZED ARCWISE CONNECTED FUNCTIONS
- NABLA-HUKUHARA DERIVATIVE OF FUZZY-VALUED FUNCTIONS ON TIME SCALES
- FROM LEIBNIZ SUPERALGEBRAS TO LIE-YAMAGUTI SUPERALGEBRAS
- ON THE UNIT GROUPS OF THE QUOTIENT RINGS OF IMAGINARY QUADRATIC NUMBER RINGS
- THE APPLICATION OF THE SECOND KIND CHEBYSHEV WAVELETS FOR SOLVING HIGH-ODER MULTI-POINT BOUNDARY VALUE PROBLEMS
- WEIGHTED NORM INEQUALITIES FOR ANISOTROPIC FRACTIONAL INTEGRAL OPERATORS

