MA Xiao-jun,YU Guo-lin,LIU San-yang

(1.Institute of Applied Mathematics,Beifang University of Nationalities,Yinchuan 750021,China)

(2.Department of Mathematics,Xidian University,Xi’an 710071,China)

Abstract:This paper is devoted to the study of relationships between vector variationallike inequalities and multi-objective programming under the assumption of generalized arcwise connected convexities.By employing the methods in convex analysis and nonsmooth analysis,the notion of(ρ,b)-right differential arcwise connected functions are introduced,and then some examples are presented to illustrate their existences.It discloses the close relationships between the efficient solutions or weakly efficient solutions of(ρ,b)-right differential arcwise connected multiobjective programming and the solutions of vector variational-like inequalities,which generalize those conclusions in the case of convexity in literatures,enrich and deepen the theory of vector optimization.

Keywords: arcwise connected convexity;vector variational-like inequality;monotonicity;multi-objective programming

1 Introduction

Convexity and its extension are of great importance in mathematical programming,which serves as an efficient concept to investigate optimality conditions.There was several extensions and generalizations for classical convexity.Among them,one meaningful notion is called arcwise connected convexity,which was first introduced by Avrie and Zang[5].Since then,several scholars have been made e ff orts to establish optimality conditions and duality results in mathematical programming under the new defined generalized arcwise connected convexities.For instance:sub-arcwise connected functions[13],arcwise cone connected type-I functions[18],arcwise connected cone-convex functions[9],arcwise connected conequasiconvex set-valued mappings[19]and B-arcwise connected functions[22],and so on.In this paper,we shall introduce a kind of generalized arcwise connected convexity,named(ρ,b)-right differential arcwise connected funtions,which are proposed by combining arcwise connected convexity together with B-invexity given in[6].

It is well-known that vector variational-like inequalities play an important role in the field of applied mathematics.In the investigation of vector variational-like inequalities,scholars are focused on the following two topics:one is the relationship between vector variational-like inequalities and vector optimization;the other one is the existence results of vector variational-like inequalities.Since Giannessi[11] first discussed the relationship between Minty vector variational inequalities and vector optimality problems in the case of differentiable functions,many results were obtained by scholars related to this topic.For example:Homidan and Ansari[2]discussed the relationship between a kind of generalized Minty vector variational-like inequalities and vector optimality problems in the case of non-differentiable functions;Ansari and Lee[4]introduced the Minty vector variational inequalities and the Stampacchia vector variational inequalities by defining upper Dini derivative,and presented an existence result for the solutions of these two kinds of variational inequalities;Yu[19],Yu and Liu[20]disclosed the relationships between proper efficiency of generalized cone-preinvex set-valued optimization problem and a kind of vector variationallike inequalities;Kim et al.[21]discussed solution existence,stability and global error bound for strongly pseudomonotone variational inequalities.

This paper is a further study of Stampacchia and Minty vector variational-like inequalities involving the generalized arcwise connected convex functions.Under the assumption of(ρ,b)-right differential arcwise connected convexity,we show the close relationships between two kinds of vector variational-like inequalities and multi-objective programming.This paper is arranged as follows:Section 2 is concerned with some definitions,which will be applicable in proving our results.In Section 3,some relationships between vector variational-like inequalities and multi-objective programming are derived.

2 Notations and Preliminaries

Let Rn,R,R+and R++be n-dimensional Euclidean space,the set of real numbers,the set of nonnegative real numbers and the set of positive real numbers.For arbitrary x,y∈Rn,the inner product between x and y is denoted by xTy.The following convention for vectors in Rnwill be followed

Let us recall the notions of arcwise connected convexity for a set and a function.

Definition 2.1[10]A set X?Rnis said to be arcwise connected,if for any x,u∈X,there exists a continuous vector-valued function Hx,u:[0,1]→X,named an arc,such that

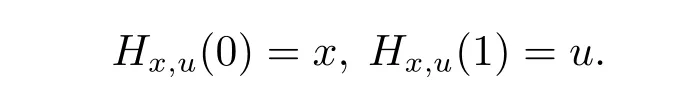
Definition 2.2[5]Let φ be a real valued function defined on an arcwise connected set X ?Rn.Let x,u∈X and Hx,ube the arc connecting x and u in X.The function φ is said to possess a right derivative or right differential with respect to the arc Hx,uat t=0 if

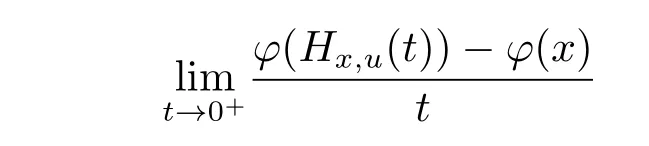
exists.This limit is denoted by φ+(Hx,u(0)).

Definition 2.3[20]Let X?Rnbe arcwise connected set.A function φ:X→R is called to be(ρ,b)-right differential arcwise connected with respect to Hx,uat x ∈ X,if there exist real valued functions b:X×X→R+,ρ:X×X→R such that

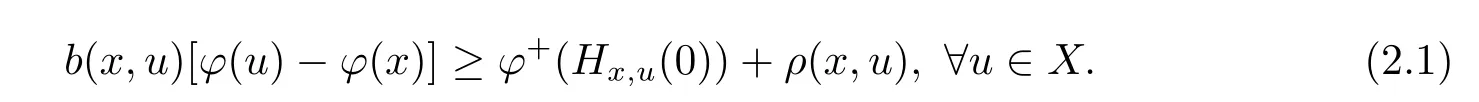
If φ is(ρ,b)-right differential arcwise connected at for all x ∈ X,then φ is called(ρ,b)-right differential arcwise connected on X;φ is called to be strictly(ρ,b)-right differential arcwise connected with respect to Hx,uat x∈X,if equation(2.1)takes strict inequality,that is

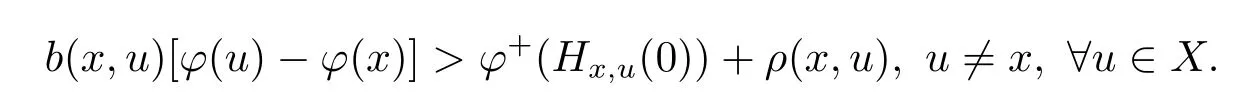
If φ is strictly(ρ,b)-right differential arcwise connected at for all x ∈ X,then φ is called strictly(ρ,b)-right differential arcwise connected on X.

Following example enables us to illustrate the above definition.

Example 1 Considering the functions φ :[0,1]→ R,b:[0,1]×[0,1]→ R+and ρ :[0,1]× [0,1]→ R,defined by φ(x)=x2,b(x,u)=x4, ρ(x,u)=0.Further,for any u,x∈[0,1],define?t∈[0,1].Then by definition of right derivative of φ,we obtain φ+(Hx,u(0))=0.Taking x=0,we have φ(u)? φ(x)=u2.Therefore we get

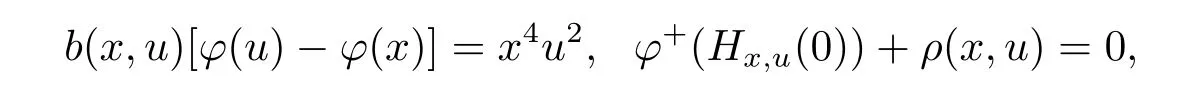
it is obvious that for x∈[0,1],

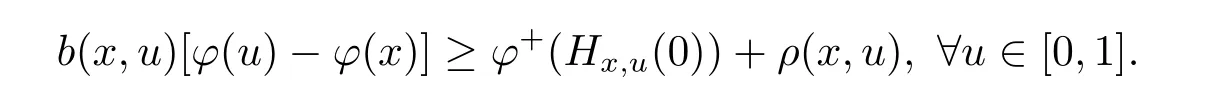
Thus φ is(ρ,b)-right differential arcwise connected with respect to Hx,uat x=0.

Definition 2.4 Let X?Rnbe arcwise connected set,a function φ:X→R is called to be pseudo(ρ,b)-right differential arcwise connected with respect to Hx,uat x ∈ X,if there exist real valued functions b:X×X→R+,ρ:X×X→R such that

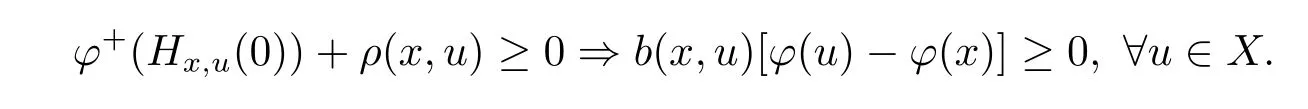
Equivalently,

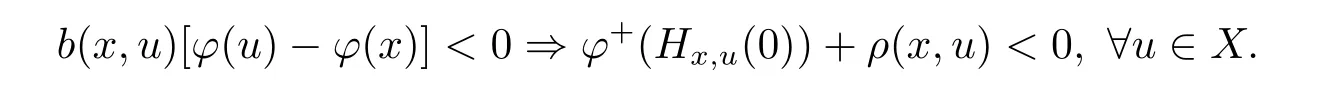
Example 2 Consider the functions φ :[0,1]7→ R,b:[0,1]× [0,1]7→ R+and ρ :[0,1]× [0,1]→ R,defined by φ(x)=x2,b(x,u)=1,ρ(x,u)= ?2x2.Further,for any u,x∈[0,1],define?t∈[0,1].Then we obtain

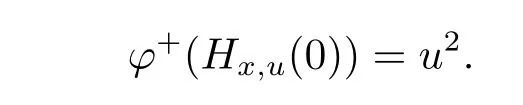
Assuming that φ+(Hx,u(0))+ ρ(x,u)≥ 0,that is

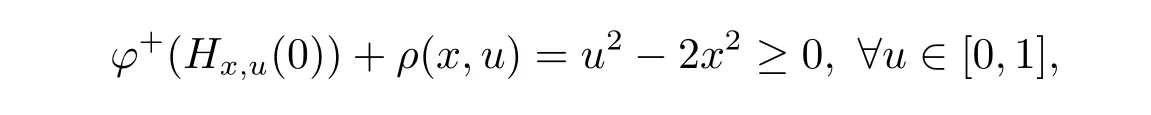
we derive f(u)? f(x)=u2? x2≥ 0.This shows that φ is pseudo(ρ,b)-right differential arcwise connected with respect to Hx,uat all x∈[0,1].

Definition 2.5 The right derivative of function φ:X?Rn→R is called monotone on X,if there exists real valued function ρ:X×X→R such that

Now,we give an example,which illustrate the monotonicity of right derivative for a real valued function.

Example 3 Consider the function φ :(0,1]→ R, ρ:(0,1]×(0,1]→ R defined by

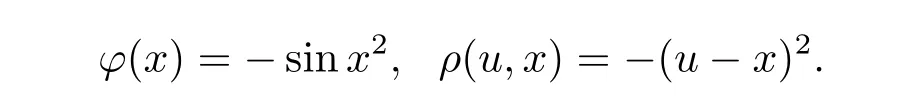
Further,for any u,x∈X,defining?t∈[0,1].Then

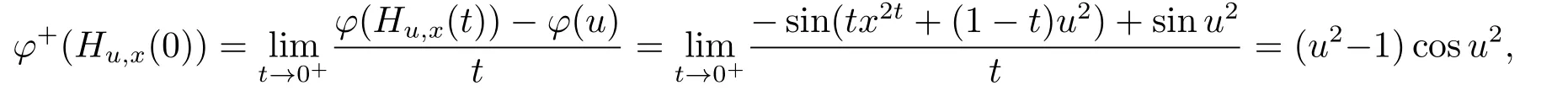
and φ+(Hx,u(0))=(x2?1)cosx2.Thus for any x,u ∈ (0,1],one has

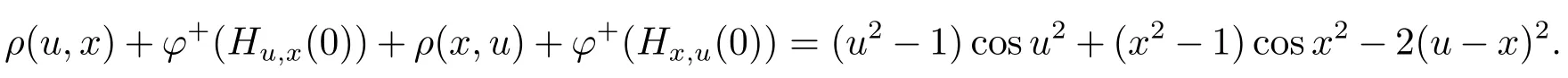
It is clear that ρ(u,x)+φ+(Hu,x(0))+ρ(x,u)+φ+(Hx,u(0))≤ 0.Therefore the right derivative of function φ is monotone on(0,1].

From now on,unless otherwise specified we always assume that X?Rnis an arcwise connected subset of Rn,f(x)=(f1(x),f2(x),···,fp(x))T,fi:X → R and fiis(ρ,b)-right differential arcwise connected function,i∈ P={1,2,···,p}.

Consider the following multi-objective programming problem

Definition 2.6 A point x∈X is said to be an efficient solution of(MOP),if there exists no u∈X such that fi(u)?fi(x)≤0,?i∈P with strict inequality for at least one i.

Definition 2.7 A point x∈X is said to be a weak efficient solution of(MOP),if there exists no u∈X such that fi(u)?fi(x)<0,?i∈P.

Next,we are about to introduce the following Stampacchia and Minty arcwise connected vector variational-like inequalities,respectively,with also their weak formulations.

(SVVI)For a given function ρi,i∈ P, find x ∈ X such that there is no u ∈ X,ful filling

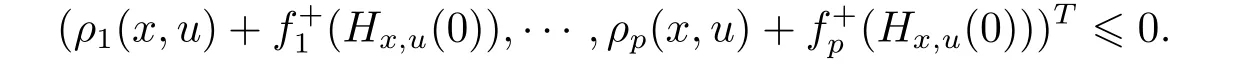
(MVVI)For a given function ρi,i∈ P, find x ∈ X such that there is no u ∈ X,ful filling

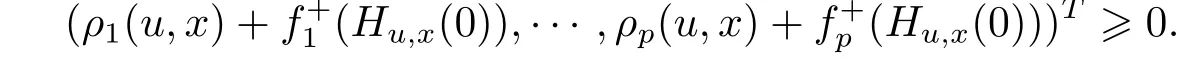
(WSVVI)For a given function ρi,i∈ P, find x ∈ X such that there is no u ∈ X,ful filling

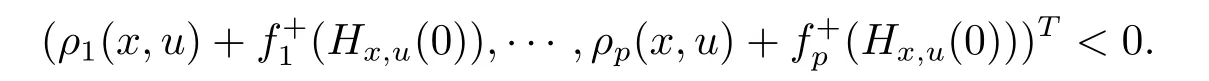
(WMVVI)For a given function ρi,i∈ P, find x ∈ X such that there is no u ∈ X,ful filling

Example4 Consider the functions f:[0,1]→ R2,ρi:[0,1]×[0,1]→ R,i=1,2,defined by f(x)=(f1(x),f2(x))T,f1(x)=x2,f2(x)=x4, ?x ∈ [0,1],and ρ1(u,x)= ρ2(u,x))=0 for u,x∈[0,1].Let?t∈[0,1].Then

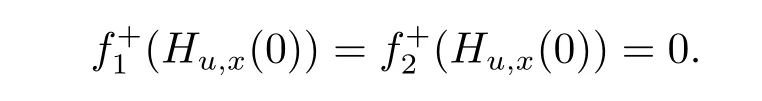
Thus

It is obvious that for x∈[0,1],there exists no u∈[0,1],satis fing

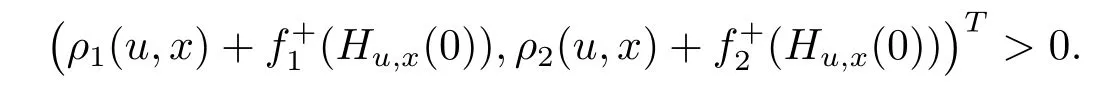
Therefore,each number in[0,1]is a solution of(WMVVI).

3 Relationship between Arcwise Connected Vector Variational-Like Inequalities and Multi-Objective Programing

In this section,we work on the relationships between Stampacchia and Minty vector variational-like inequalities and multi-objective programming,which are formulated in Section 2.

Theorem3.1 Let u be arbitrary vector in X,bi:X×X →R++,ρi:X×X →R,i∈P and for each i∈ P,fi:X → R is(ρi,bi)-right differential arcwise connected with respect to Hx,uat x∈X.If x solves(SVVI),then x is an efficient solution of(MOP).

Proof Suppose that x is not an efficient solution of(MOP),then there exists u∈X such that

with strict inequality for at least one i.Because,for each i∈ P,fiis(ρi,bi)-right differential arcwise connected with respect to Hx,uat x∈X,it follows from Definition 2.3 that

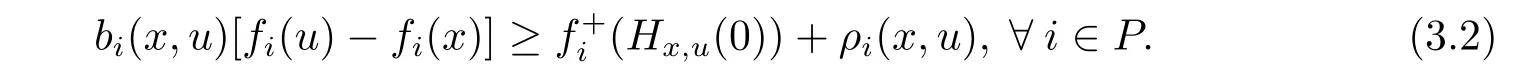
Noticing that bi(x,u)>0,we derive from(3.1)and(3.2)that ρi(x,u)+f+i(Hx,u(0)) ≤ 0 with strict inequality for at least one i.This shows that there exists u∈X such that

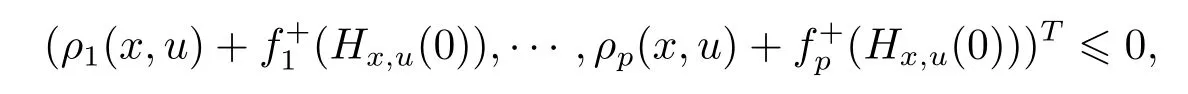
which is a contradiction to the fact that x solves(SVVI).

Theorem 3.2 Let u be arbitrary vector in X,bi:X×X→R++,ρi:X×X→R+,i∈ P and for each i∈ P,?fi:X → R is strictly(ρi,bi)-right differential arcwise connected with respect to Hx,uat x∈X.If x is a weak efficient solution of(MOP),then x solves(SVVI).

Proof We proceed by contradiction.Assume that x is a weak efficient solution of(MOP),but does not solve(SVVI).Then there exists u∈X such that

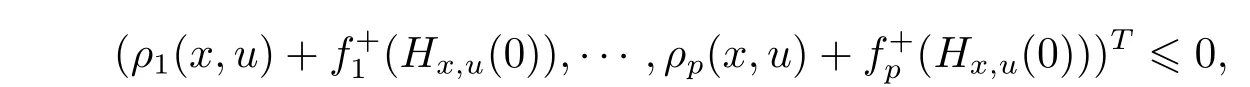
that is,there exists u∈X such that

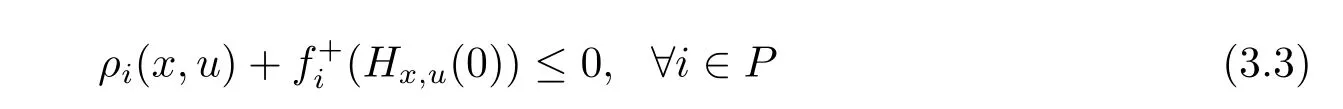
with strict inequality for at least one i.Because,for each i∈ P, ?fiis strictly(ρi,bi)-right differential arcwise connected with respect to Hx,uat x∈X,it follows from Definition 2.3 that

By(3.3)and(3.4),we obtain that there exists u∈X such that fi(u)?fi(x)<0,?i∈P,which contributes to a contradiction.Hence x is a solution of problem(SVVI).

Theorem 3.3 Let u be arbitrary vector in X,bi:X×X →R++,ρi:X×X →R,i∈P and for each i∈ P,fi:X → R is pseudo(ρi,bi)-right differential arcwise connected with respect to Hx,uat x∈X.If x solves(WSVVI),then x is a weak efficient solution of(MOP).

Proof We proceed by contradiction.Assume that x is not a weak efficient solution of(MOP),namely,there exists u∈X such that fi(u)?fi(x)<0,?i∈P.Since,for each i∈ P,fiis pseudo(ρi,bi)-right differential arcwise connected with respect to Hx,uat x ∈ X,hence,for u∈X,we can derive

That is,there exists u∈X such that

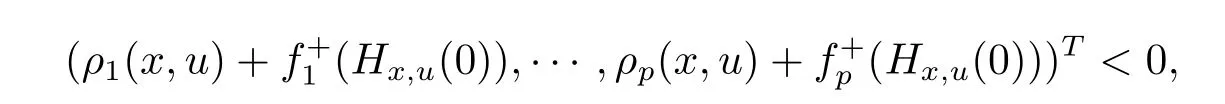
which leads to a contradiction.

Theorem 3.4 Let u,x∈X be arbitrary vectors,bi:X×X→R++,ρi:X×X→R,i∈ P and for each i∈ P,fi:X → R is(ρi,bi)-right differential arcwise connected with respect to Hu,xon X.If x is an efficient solution of(MOP),then x solves(MVVI).

Proof Suppose,contrary to the result,that x does not solve(MVVI),then there exists u∈X,such that

That is,there exists u∈X such that

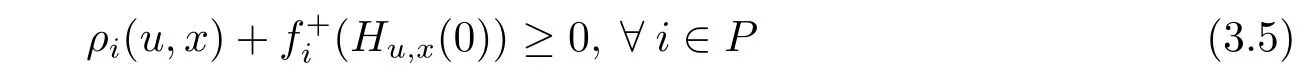
with strict inequality for at least one i.Because,for each i∈ P,fiis(ρi,bi)-right differential arcwise connected with respect to Hu,xon X,so we have

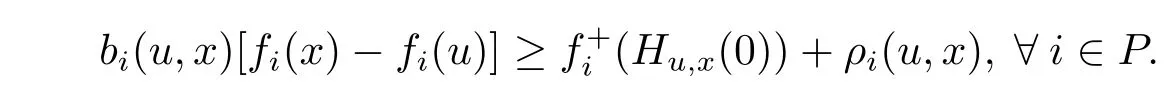
By condition(3.5)and the above inequality,it follows that there exists u∈X,satisfying

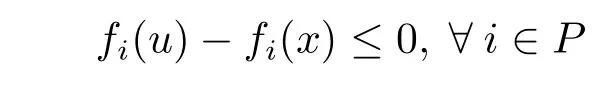
with strict inequality for at least one i,which contradicts the hypothesis that x is an efficient solution of(MOP).

Theorem 3.5 Let u,x∈X be arbitrary vectors,ρi:X×X →R,i∈P and for each i∈P,the right derivative of fi:X→R is monotone on X.If x∈X solves(WSVVI),then x solves(WMVVI).

ProofSuppose x solves(WSVVI),then there exists no u∈X,such that

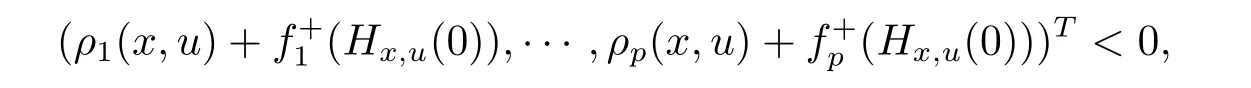
i.e.,there exists u∈X such that

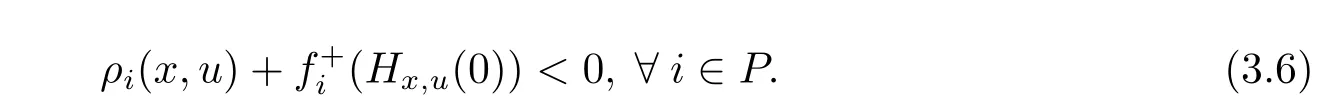
Because,for each i∈P,the right derivative of fiis monotone on X,we have

The above inequality can be rewritten as,for all x,u∈X and i∈P,we get

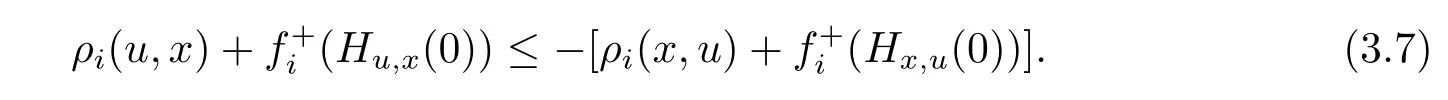
By inequalities(3.6)and(3.7),it follows that,there exists no u∈X such that

That is,there exists no u∈X,such that

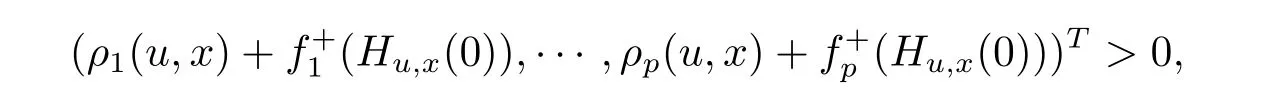
which implies that,x solves(WMVVI).

Theorem 3.6 Let u,x∈X be arbitrary vectors,bi:X×X→R++,ρi:X×X→R,i∈ P and for each i∈ P,fi:X → R is strictly(ρi,bi)-right differential arcwise connected with respect to Hu,xon X.If x is a weak efficient solution of(MOP),then x solves(MVVI).

Proof We proceed by contradiction.Suppose that x is a weak efficient solution of(MOP)but does not solve(MVVI),then there exists u∈X,satisfying

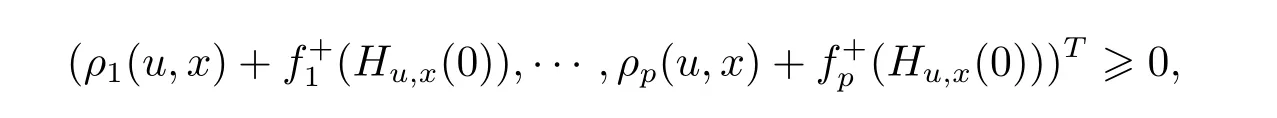
that is,there exists u∈X such that

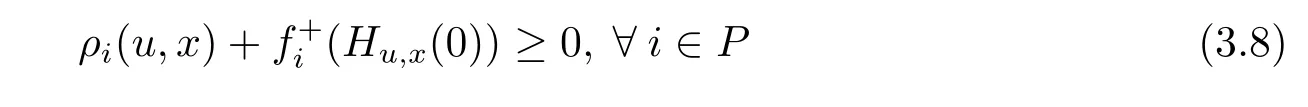
with strict inequality for at least one i.Because,for each i∈ P,fiis strictly(ρi,bi)-right differential arcwise connected with respect to Hu,xon X,so we have

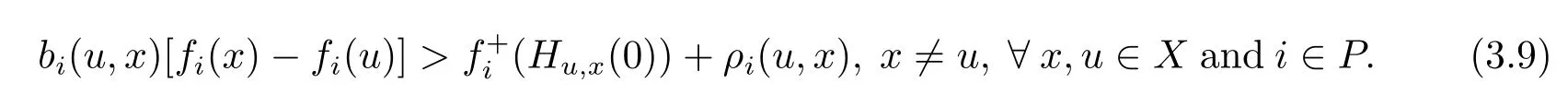
From(3.8)and(3.9),it follows,there exists u∈X such that fi(u)?fi(x)<0,?i∈P,which contradicts the fact that x is a weak efficient solution of(MOP).

Theorem 3.7 Let u,x∈X be arbitrary vectors,bi:X×X→R++,ρi:X×X→R,i∈ P and for each i∈ P,fi:X → R is(ρi,bi)-right differential arcwise connected with respect to Hu,xon X.If x is a weak efficient solution of(MOP),then x solves(WMVVI).

ProofThe proof is similar to that of Theorem 3.4 and therefore being omitted.