GLOBAL HYPOELLIPTIC ESTIMATE FOR LANDAU OPERATOR WITH EXTERNAL POTENTIAL
LIU Lv-qiao
(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
1 Introduction and Main Results
We may recall here that the Landau equation reads as the evolution equation of the density of particles
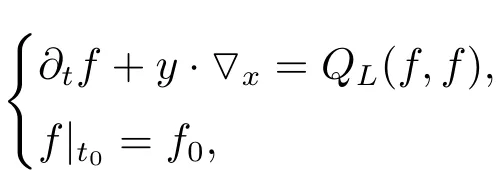
where QLis the so-called Landau collision operator

here,a(y)is a symmetric nonnegative matrix depending on a parameter y∈R3,

and
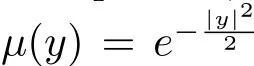

We consider the Landau-type operator with external potential
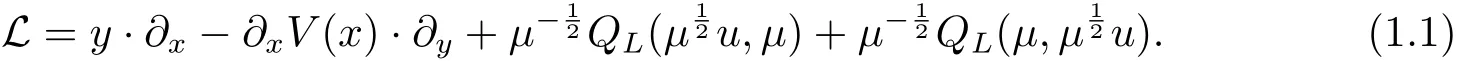
In the linear homogeneous case,Fokker-Planck equations,Landau equations and Boltzmann equations equations have then a parabolic behavior,and the study of the local smoothing properties in the velocity variable is rather direct.In the non-homogeneous case,the regularization in space variable is not so easy,but occurs anyway thanks to the so-called hypoelliptic structure of the equation.In this article,we are interested in global estimates of the following Landau operator
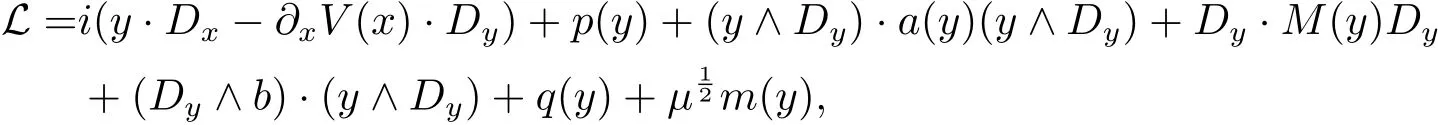
where Dx= ?i?x,Dy= ?i?y,and x ∈ R3is the space variable and y ∈ R3is the velocity variable,and X·Y stands for the standard dot-product on R3.The real-valued function V(x)of space variable x stands for the macroscopic force,M(y)is a metric and the functions a(y),b(y)and p(y)of the variable y in the diffusion are smooth and real-valued with the properties subsequently listed below.
(1)There exists a constant c>0 such that
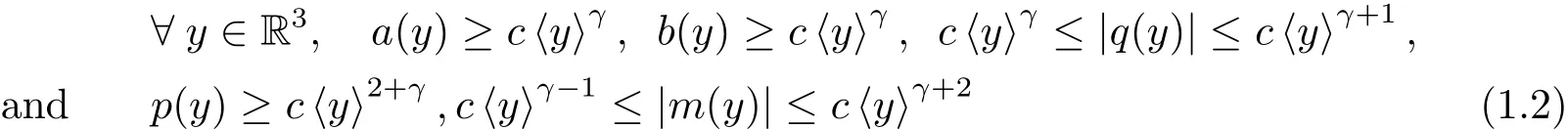
(2)For any α ∈,there exists a constant Cαsuch that

(3)M(y)is a positive de finite matrix with
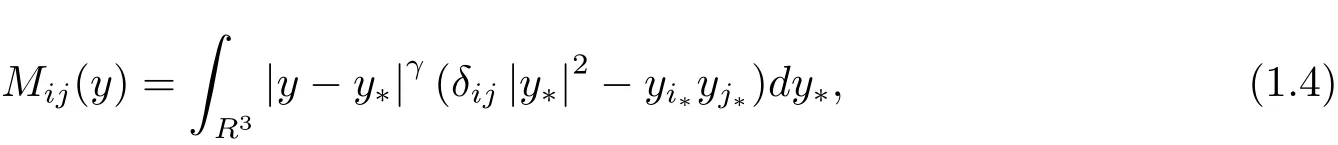
here we can substitute Dy·F(y)Dyfor Dy·M(y)Dywith F(y)〈y〉γ.It is sometimes convenient to rewrite the operator as the form
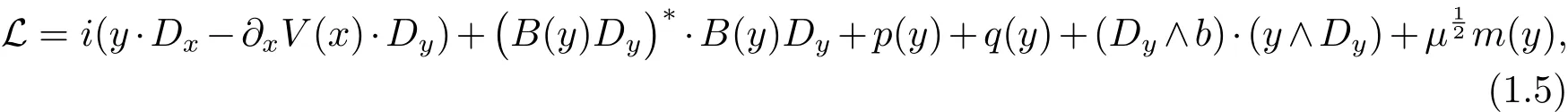
where the matrix B(y)is given by
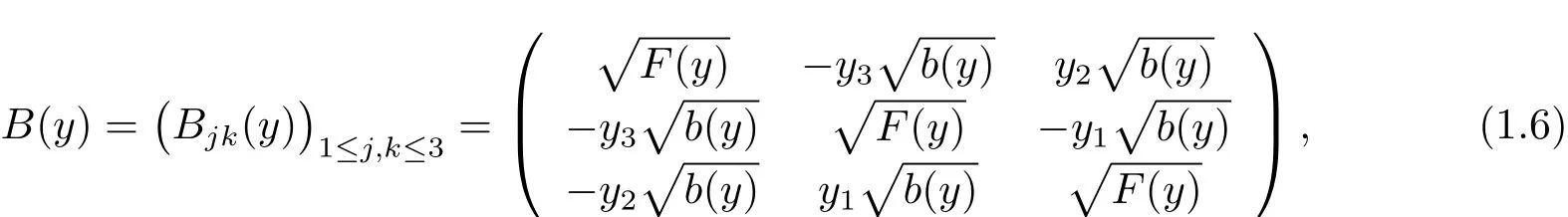
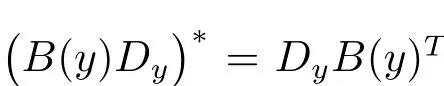
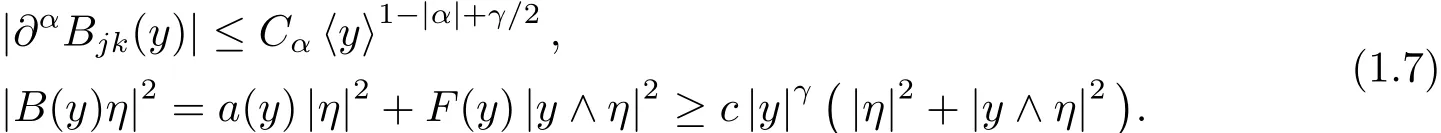
Denoting by(ξ,η)the dual variables of(x,y),we notice that the diffusion only occurs in the variables(y,η),but not in the other directions;and that the cross product term y∧Dyimproves this diffusion in speci fic directions of the phase space.In[3],the authors gave a estimate of the main term to the operator L.In this work,we aim at dealing with the low order terms to linear Landau-type operators and giving a similar results.Our main results can be stated as follows.
Theorem 1.1Let V∈C2(R3;R)satisfy that
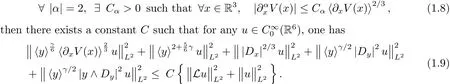
Estimates of the type given in Theorem 1.1 can be analyzed through different point of views.At first they give at least local regularity estimates in the velocity direction,according to the term|Dy|2appearing in(1.9).Now one of the goal of this article was to give global estimates in order to identify the good functional spaces associated to the problems.
The second main feature of this result is to re flect the regularizing effect in space variable x,thanks to the hypoelliptic structure,which leads to terms involving e.g.|Dx|2/3.Recall that the exponent 2/3 here is optimal.
Now similarly to the case of elliptic directions,it may be interesting to get global weighted estimates in space direction.In[7,9],the authors studied the Fokker-Planck case,in particular with a potential.In this direction,the work[4]also gave a first subelliptic global(optimal)estimate,concerning the Landau operator in the case when there is no potential;the main feature of that work was to show that subellipticity in space direction occured with anisotropic weights of type 〈y〉γy ∧ Dx.In the present article,we first give complete form of operator and recover the same type of behavior,with additional terms also involving wedges linked with the potential V.
The present work is a natural continuation of[1,3,4],and as there we will make a strong use of pseudodifferential calculus.
2 Notations and Some Basic Facts
We first list some notations used throughout the paper.Denote respectively byandthe inner product and the norm in L2(Rn).For a vector-valued functions U=
To simplify the notation,by AB we mean there exists a positive constant C,such that A≤CB,and similarly for AB.While the notation A≈B means both AB and BA hold.
Now,we introduce some notations of phase space analysis and recall some basic properties of symbolic calculus,and refer to[8]and[11]for detailed discussions.Throughout the paper let g be the admissible metric|dz|2+|dζ|2and m be an admissible weight for g(see[8]and[11]for instance the de finitions of admissible metric and weight).Given a symbol p(z,ζ),we say p ∈ S(m,g)if
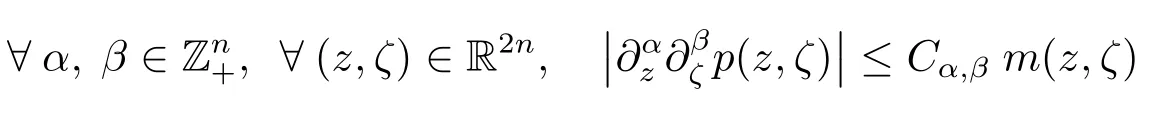
with Cα,βa constant depending only on α,β.For such a symbol p we may de fine its Weyl quantization pwby The L2continuity theorem in the class S(1,g),which will be used frequently,says that if p∈ S(1,g)then
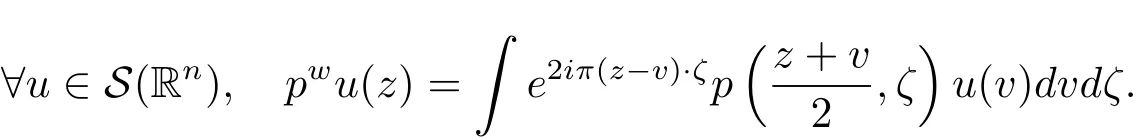
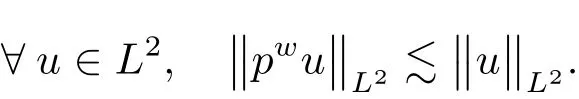
We shall denote by Op(S(m,g))the set of operators whose symbols are in the class S(m,g).Finally,let’s recall some basic properties of the Wick quantization,and refer the reader to the works of Lerner[11]for thorough and extensive presentations of this quantization and some of its applications.Using the notation Z=(z,ζ)∈ R2n,the wave-packets transform of a function u∈ S(Rn)is de fined by
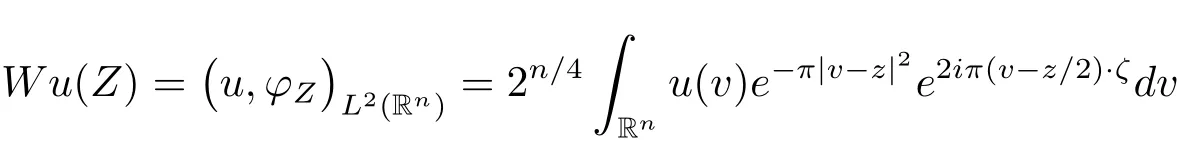
with ?Z(v)=2n/4e?π|v?z|2e2iπ(v?z/2)·η,v ∈ Rn,then one can verify that W is an isometric mapping from L2(Rn)to L2(R2n),

Moreover the operator πH=WW?,with W?the adjoint of W,is an orthogonal projection on a closed space in L2whose kernel is given by
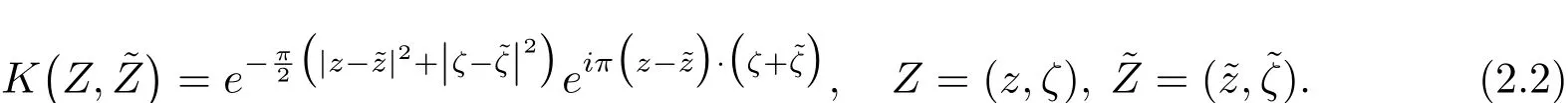
We de fine the Wick quantization of any L∞symbol p as pWick=W?pW.The main property of the Wick quantization is its positivity,i.e.,
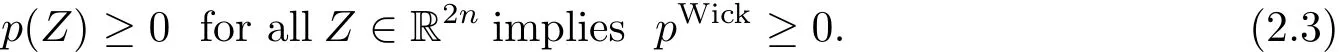
According to Proposition 2.4.3 in[11],the Wick and Weyl quantizations of a symbol p are linked by the following identities

with
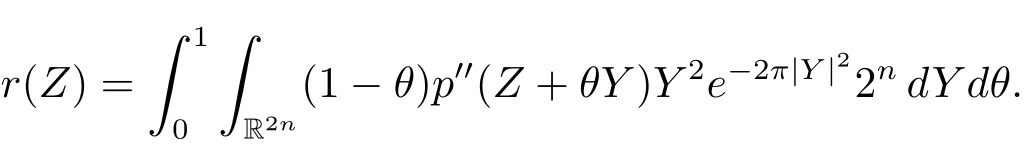
We also recall the following composition formula obtained in the proof of Proposition 3.4 in[10]

with T a bounded operator in L2(R2n),when p∈L∞(R2n)and q is a smooth symbol whose derivatives of order≥2 are bounded on R2n.The notation{p,q}denotes the Poisson bracket de fined by

3 The Proof of Theorem 1.1:Weighted Estimates
In this section,we are mainly concerned with the estimate in weighted L2norms,that is
Proposition 3.1Let V(x)∈C2(R3;R)satisfy condition(1.8),then

In order to prove the proposition,we begin with
Lemma 3.2Considerate the operator L in(1.5),in the elliptic direction we have an estimate.For all
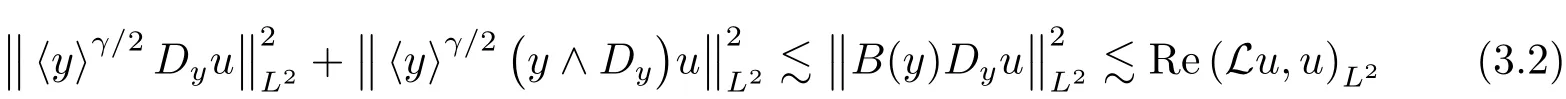
and

where(·, ·)L2andstanding for the inner product and norm in
ProofObserving i(y·Dx??xV(x)·Dy)is skew-adjoint,then
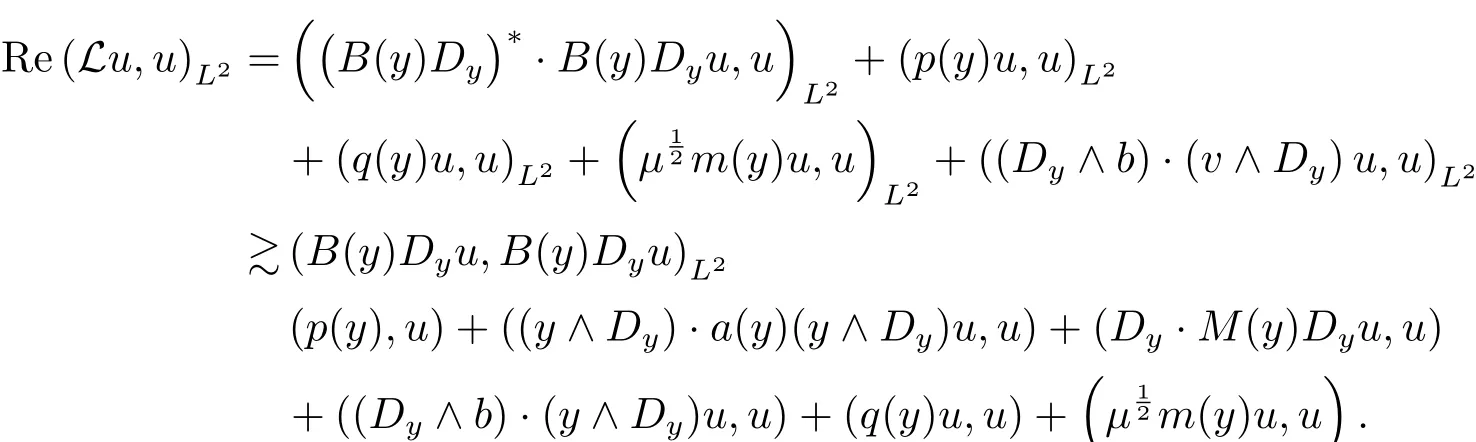
The inequality hold due to
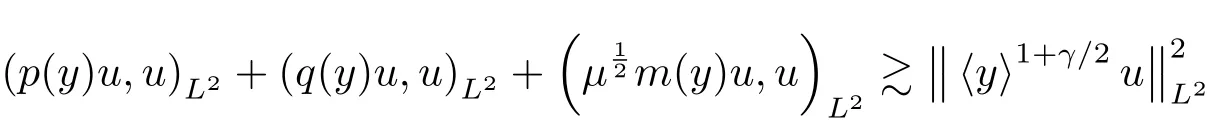
and

By(1.2)and(1.3)one has,for any y,η ∈ R3and any α ∈ Z3+,
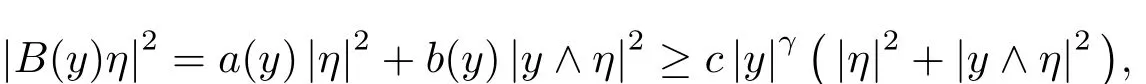
then
So we complete the lemma.

ProofWe notice that p(y)α∈ S(p(y)α,|dy|2+|dη|2),then

For the first term to(3.4),

where the third holds,since G ∈ S(1,|dy|2+|dη|2).As to the second term,
we get the third inequality from
Now,we will estimate the last term,similar to the above inequality,we get
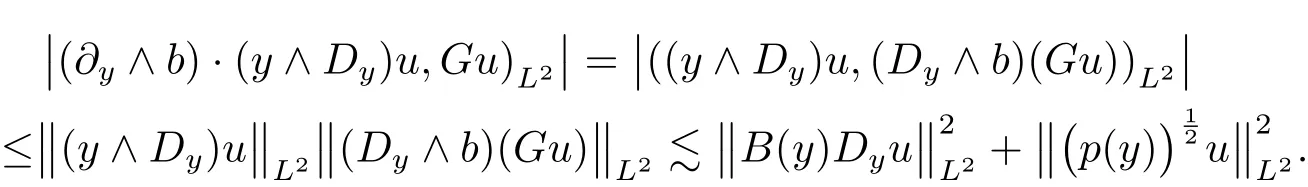
Together the above estimate and Lemma 3.2 give Lemma 3.3.
Lemma 3.4For all,we have

ProofIn this proof,we letthe conclusion will follow if one could prove
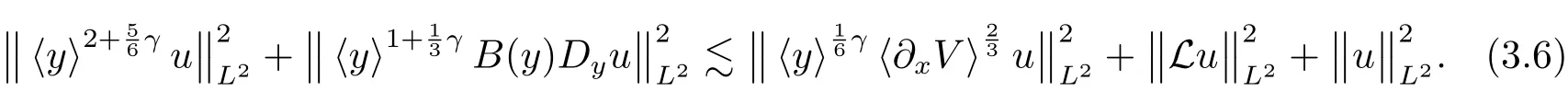

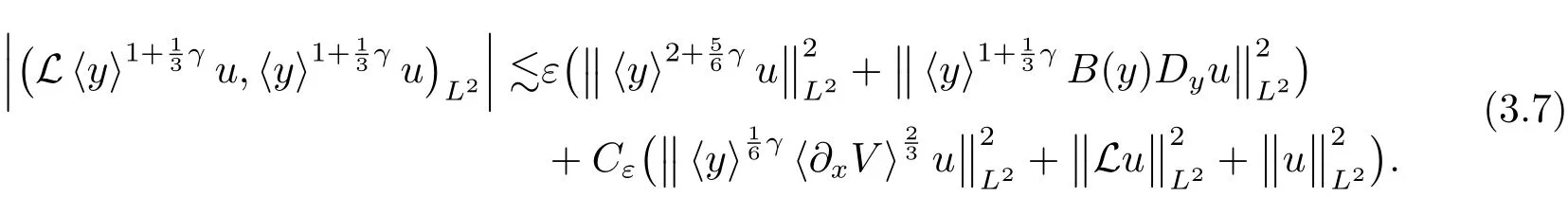
In fact,the estimate
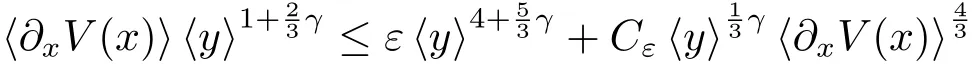
yields
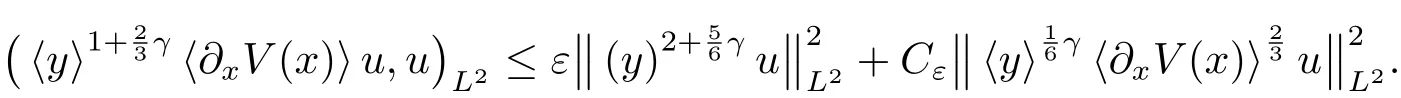
Consequently,using(1.5),we compute

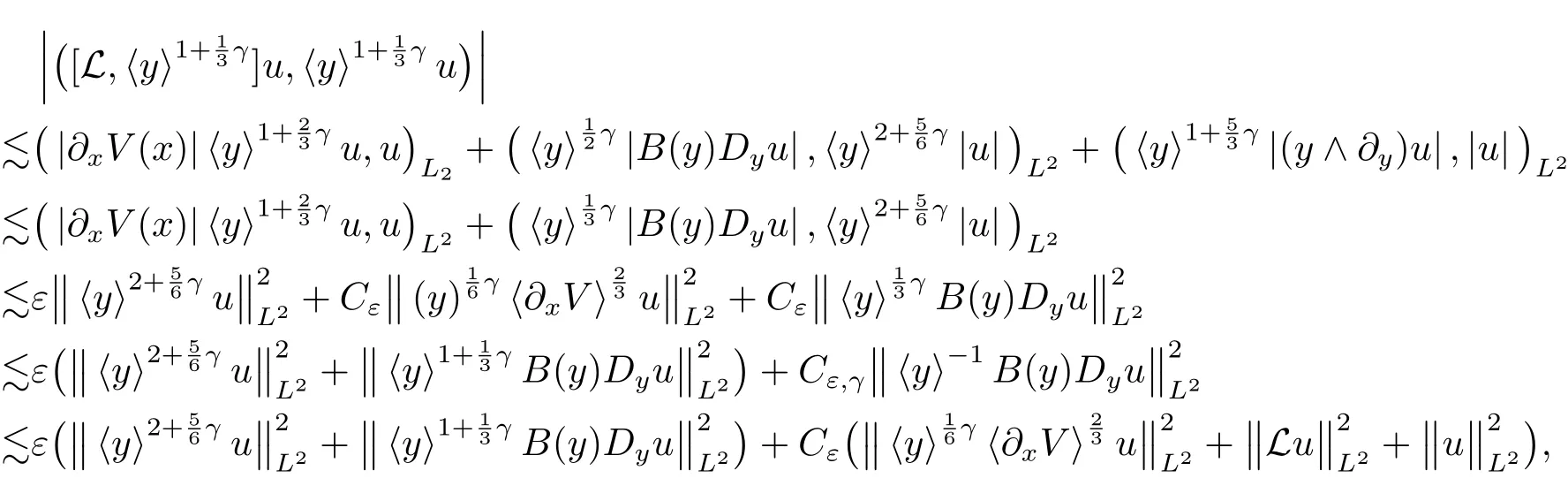
And thus where the second inquality follows from
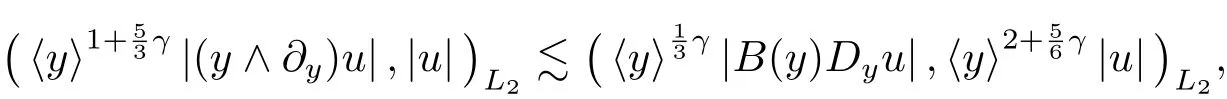
the third inquality holds due to interpolation inequality.The forth inquality holds because
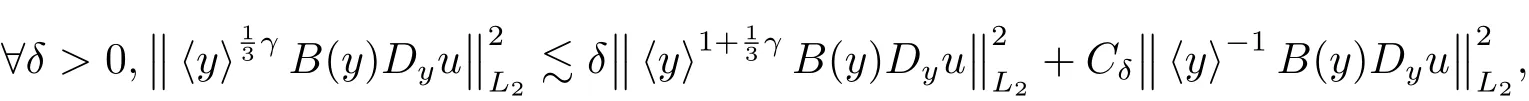
and the last inequality follows from

As a result
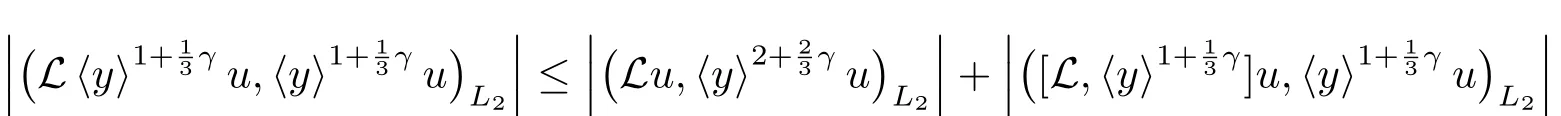
and notice that γ≥0,
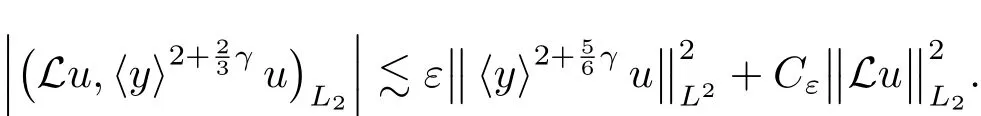
Then we gain inequality(3.7).
Now we prove(3.6).Let’s first write

the second inequality using(3.2).For the last term,we have
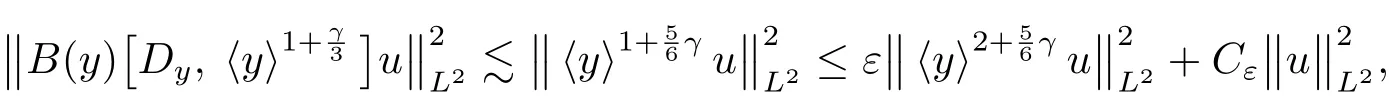
then the desired estimate(3.5)follows from the above inequalities and(3.7),completing the proof of Lemma 3.4.
Proof of Proposition 3.1Let ρ ∈ C1(R2n)be a real-valued function given by
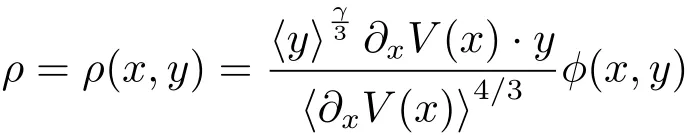
with

where χ ∈(R;[0,1])such that χ =1 in[?1,1]and supp χ ? [?2,2].So we have
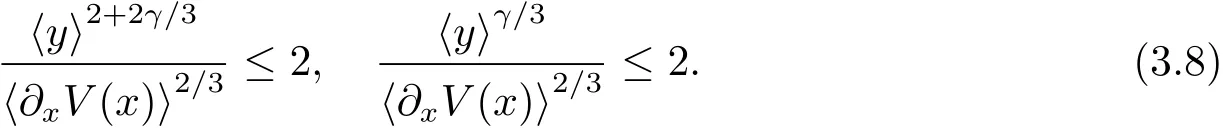
And it is easy to verify that|ρ|≤ 1.
Using the notation Q=y·Dx??xV(x)·Dy,

which along with yields Re(iQu,ρu)L2? |(Lu,u)L2|+|(Lu,ρu)L2|.Next,we want to give a lower bound for the term on the left side.Direct computation shows that
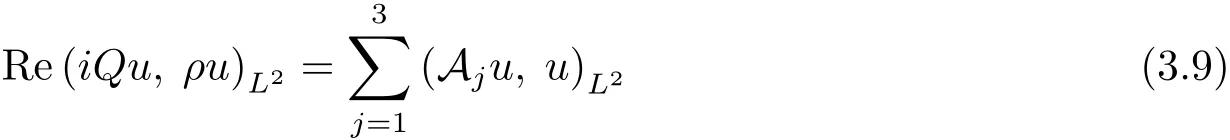
with Ajgiven by

We will proceed to treat the above three terms.First one has
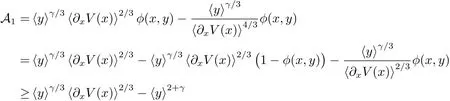
from which it follows that
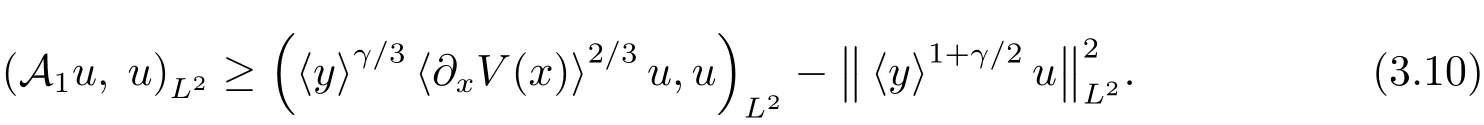
Here we used(3.8)in last inequality.As for the term A2we make use of the relation
to compute

the first inequality using the fact that
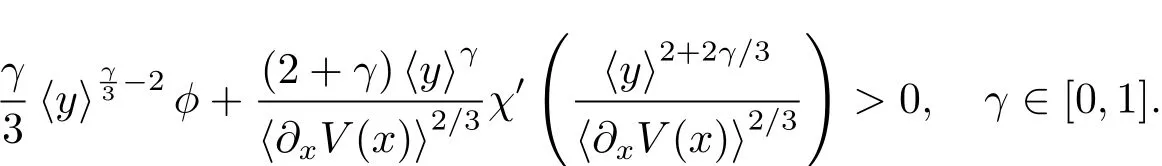
As a result,we conclude
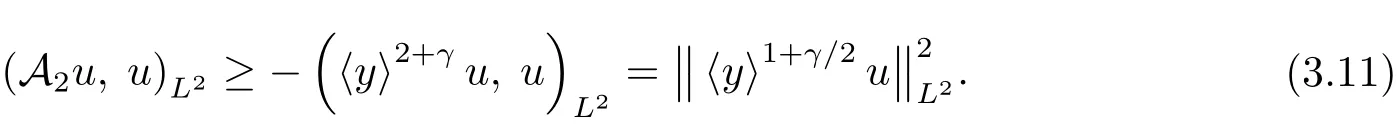
For the term A3,using(1.8)gives
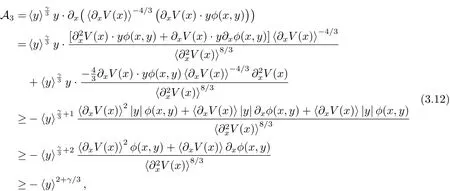
and thus
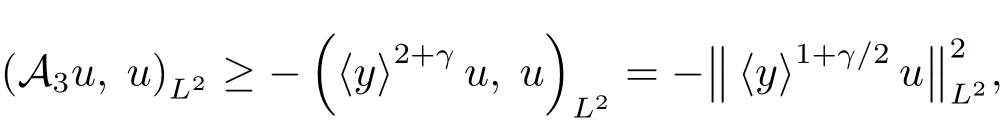
this along with(3.9),(3.10)and(3.11)shows that
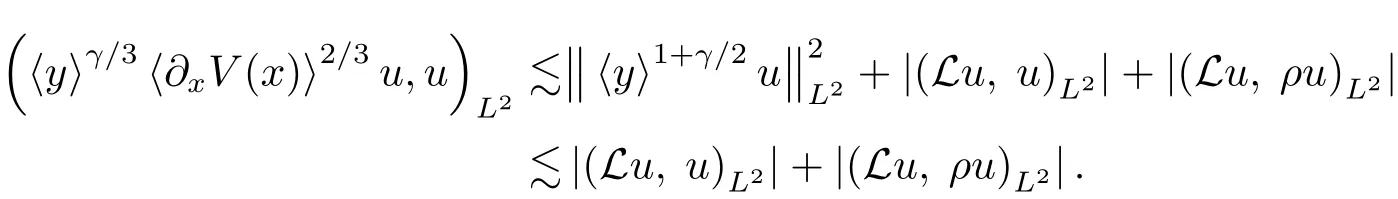
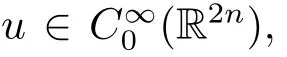
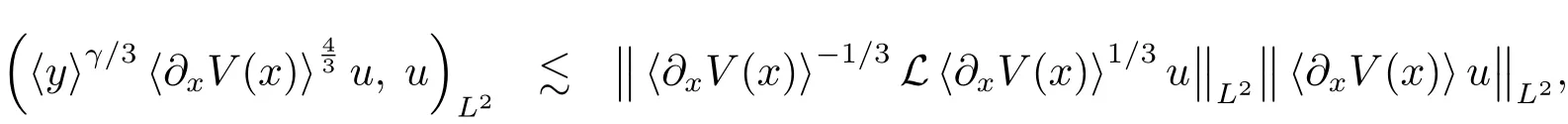
which,together with the fact that γ≥0,implies
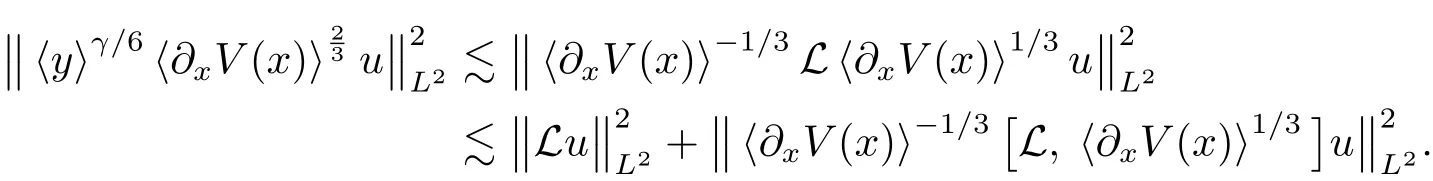
Moreover in view of(1.8),we have

Then the desired inequality(3.1)follows,completing the proof of Proposition 3.1.
4 Hypoelliptic Estimates for the Operator with Parameters
In this section,we always consider X=(x,ξ) ∈ R6as parameters,and study the operator acting on the velocity variable y,

where QX=y·ξ??xV(x)·Dyand B(y)is the matrix given in(1.6).

The main result of this section is the following proposition.
Proposition 4.1Let λ be de fined by
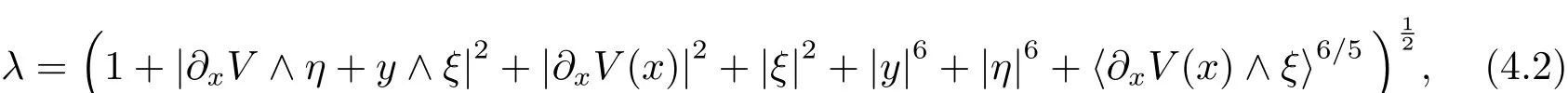
then the following estimate
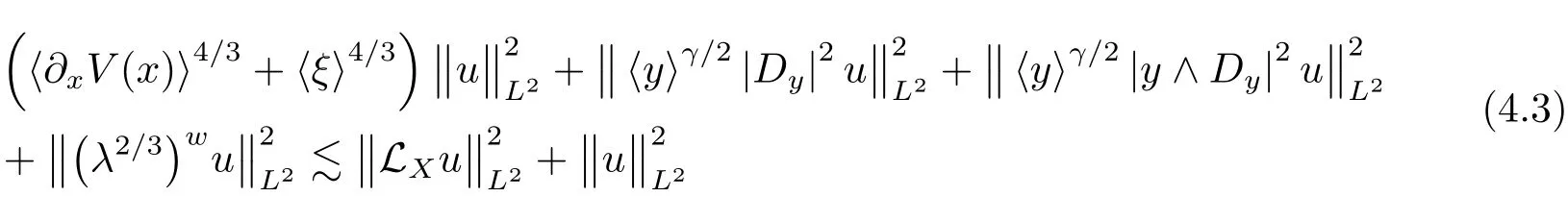
holds for all u∈S(),uniformly with respect to X.
We would make use of the multiplier method introduced in[4],to show the above proposition through the following subsections.
Before the proof of Proposition 4.1,we list some lemmas.
Lemma 4.2Let λ be de fined in(4.2),then
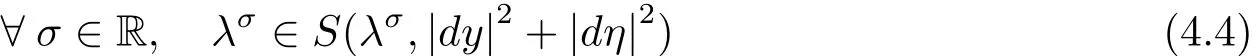


and thus
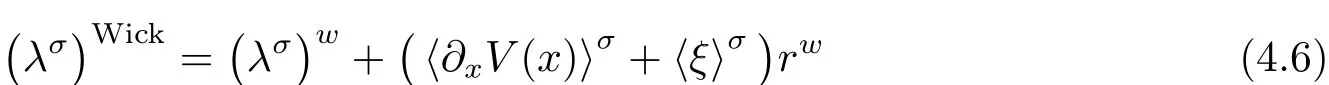

ProofBy direct veri fication,we see that for all(y,η)∈ R2nand all α,,one has
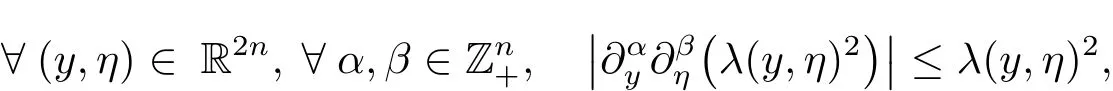
which implies(4.4).Moreover note that for

and thus

then we get(4.5)ifand thus(4.6)in view of(2.4),completing the proof of Lemma 4.2.
Lemma 4.3Let λ be given in(4.2),then for all u ∈ S(R3),one has
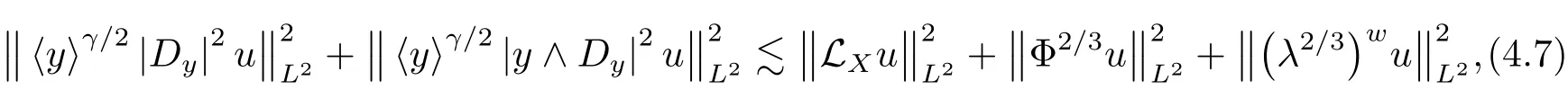
where Φ is de fined by
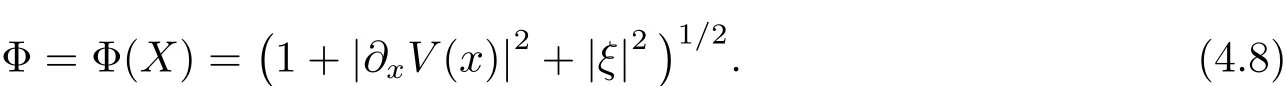
ProofSimilar to(3.2),we have,for any u∈,S(),

Using the above inequality to Dyju gives
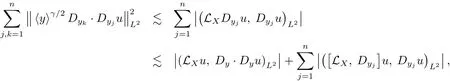
which with the fact that γ ≥ 0 implies
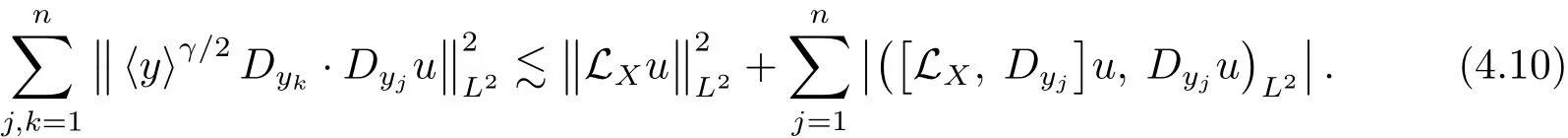
So we only need to handle the last term in the above inequality.Direct veri fication shows
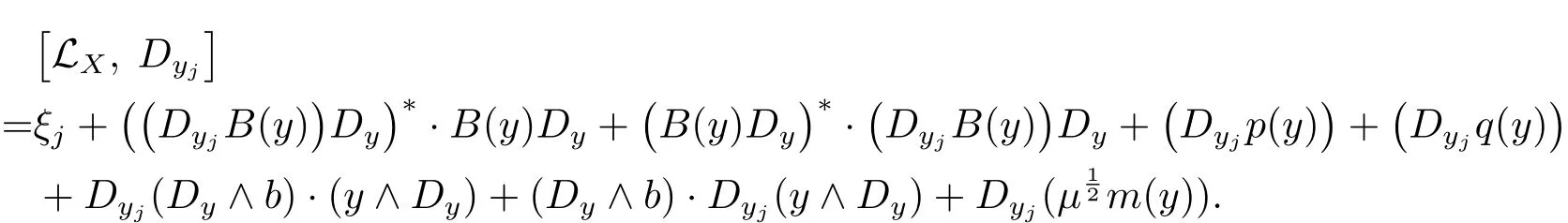
This gives
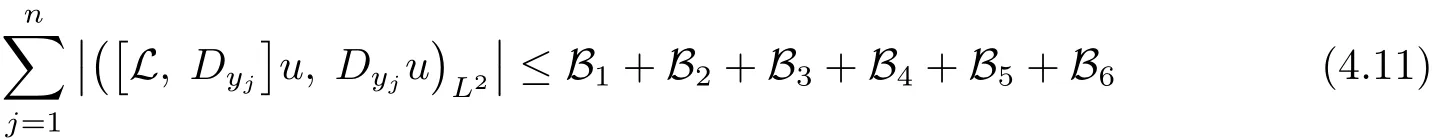
with

By Parseval’s theorem,we may write,denoting bythe Fourier transform with respect to y,and hence
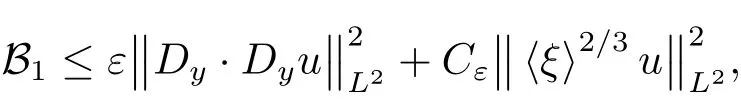
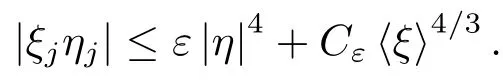
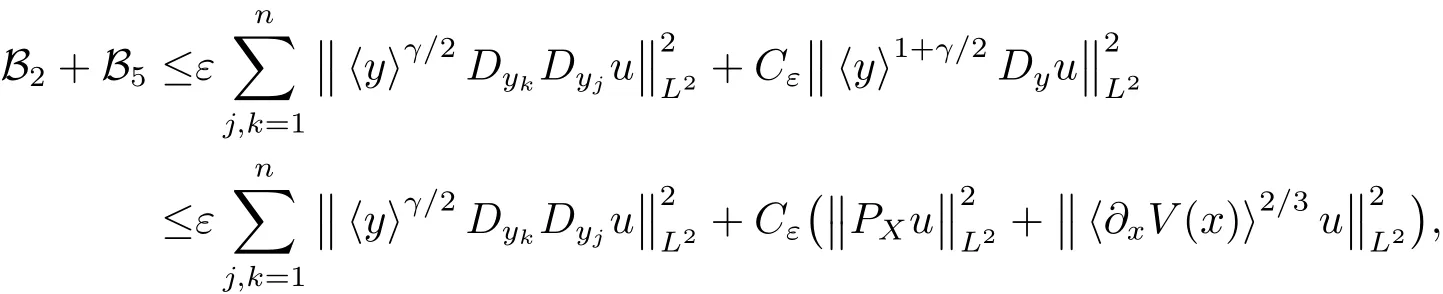
the last inequality using Lemma 3.4.
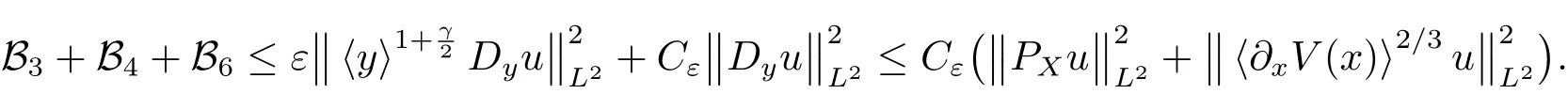
Due to the arbitrariness of the number ε,the above inequalities along with(4.10)and(4.11)gives the desired upper bound for the first term on the left side of(4.7).
It remains to treat the second term.In the following discussion,we use the notation

From(4.9),it follows that

which with the fact that γ ≥ 0 implies

In order to handle the last term in the above inequality,we write

This gives
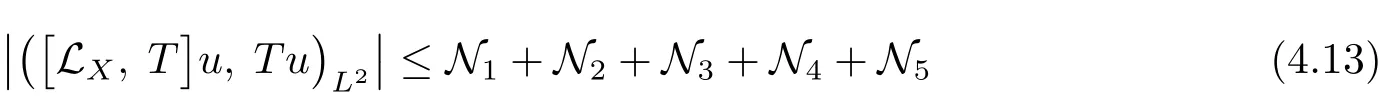

Next we proceed to treat the above four terms.For the term N1one has,with λ de fined in(4.2),
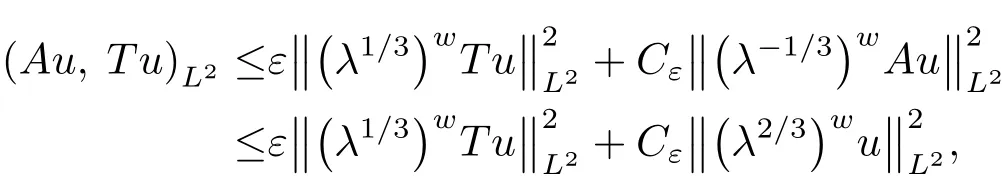

On the other hand,

Observing(4.4),symbolic calculus give that

with dj,1≤ j≤ 3,belonging touniformly with respect to X.This shows
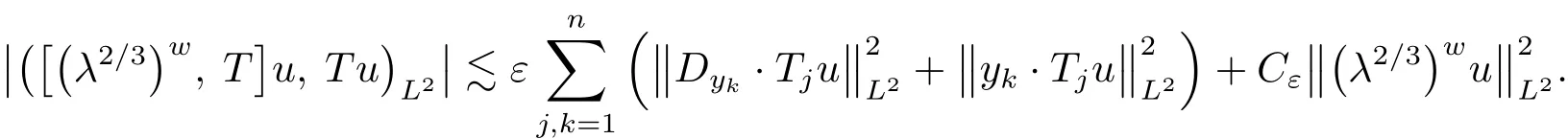
Combining the above inequalities,we have
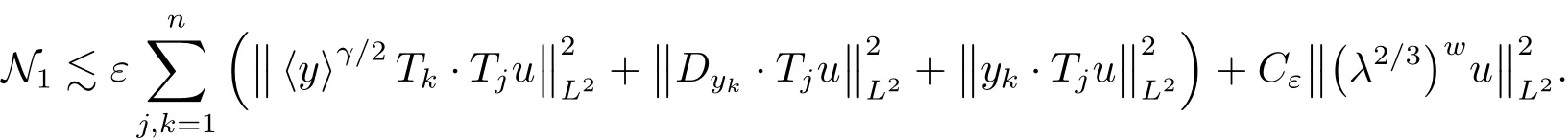
Direct veri fication shows
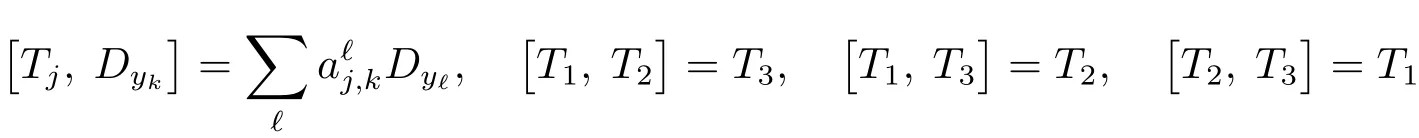
withand thus
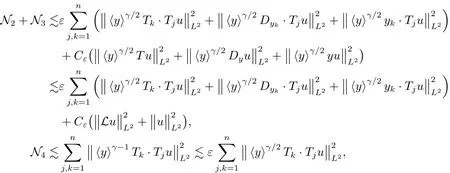
the last inequality using(3.2).It remains to treat N5,and by(1.2)and(3.2),we have
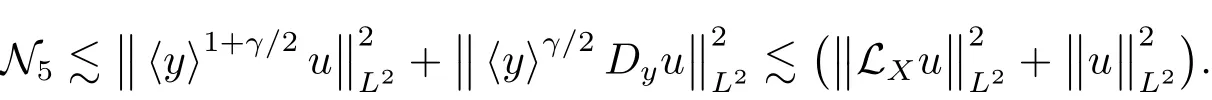
Combining the above estimates,we conclude
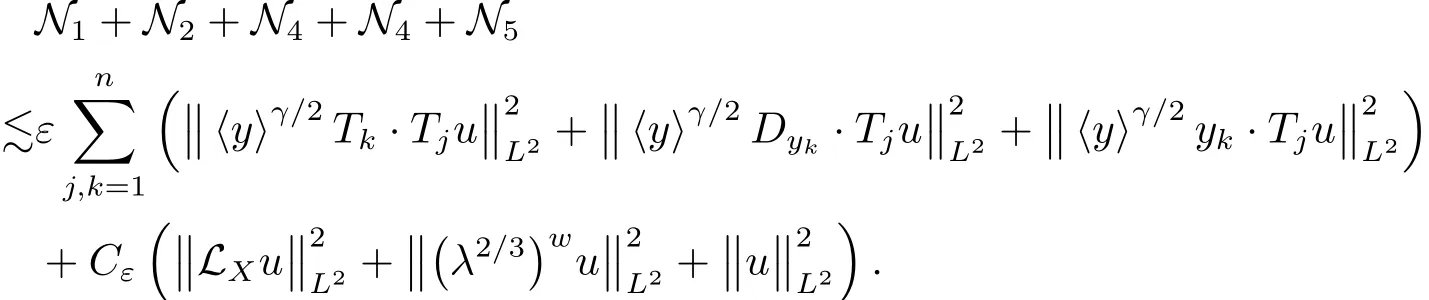
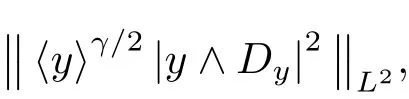
Lemma 4.4Let g ∈ S(1,|dy|2+|dη|2)uniformly with respect to X,and let λ be de fined in(4.2).Then for any ε> 0,there exists a constant Cεsuch that

where Φ is given in(4.8).
ProofAs a preliminary step we firstly show that for any ε> 0,there exists a constant Cεsuch that
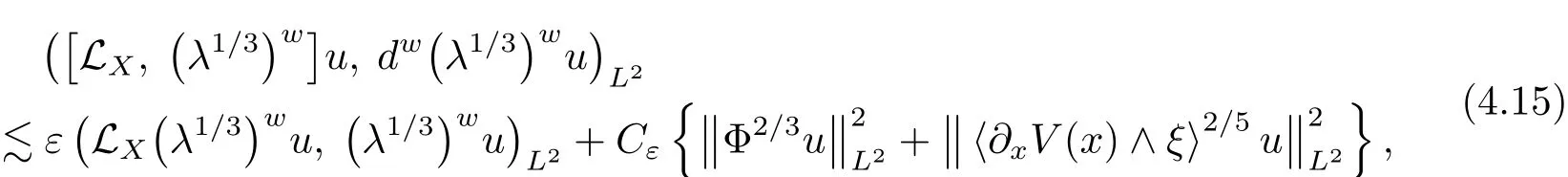

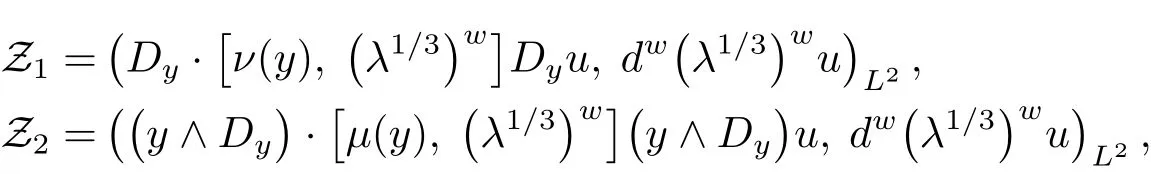
we have

The last inequality holding because
Denote
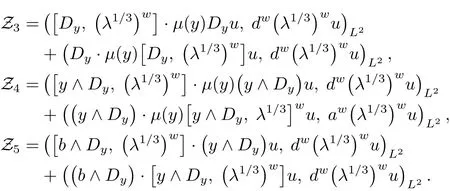
Observing(4.5),symbolic calculus give that
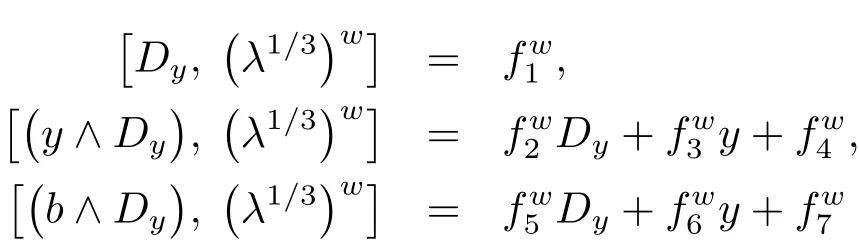
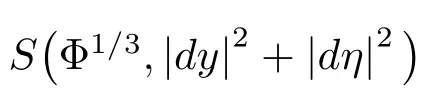
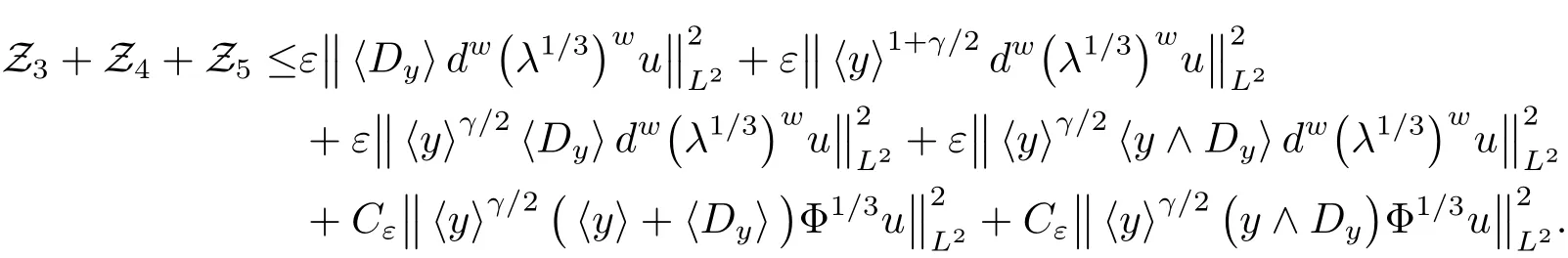
Using similar arguments as the treatment of Z1and Z2,we conclude

This along with(4.16)gives

since
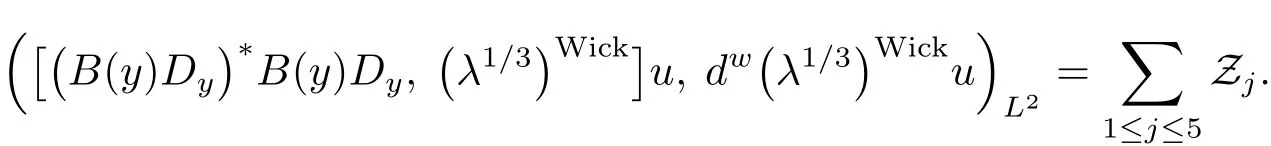
Moreover,we have
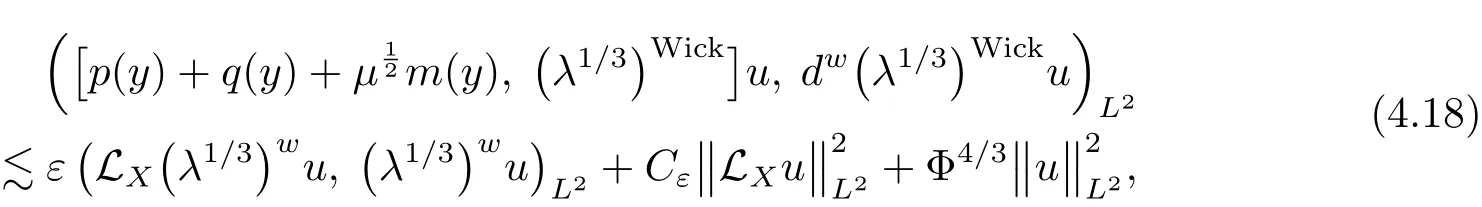
which can be deduced similarly as above,since by(1.3),
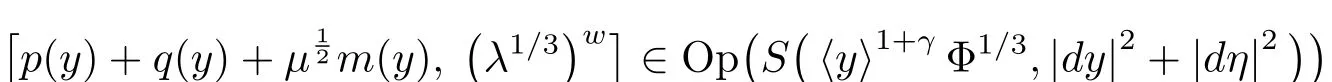
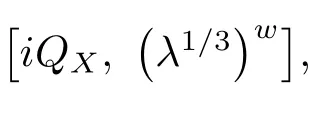
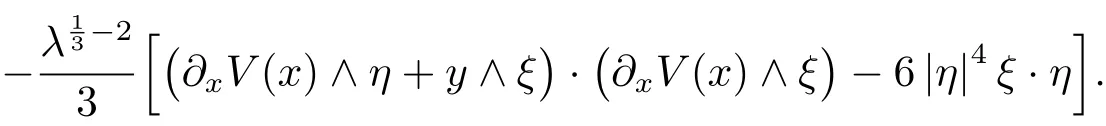
In view of(4.4)and(4.2),one could verify that the above symbol belongs to
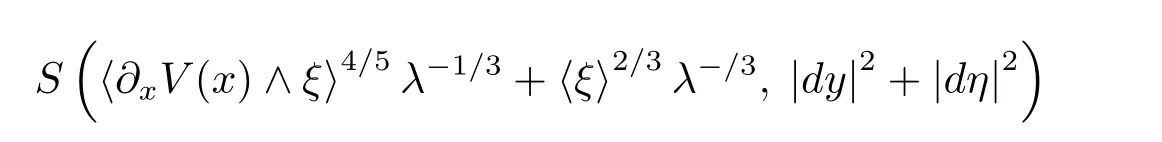
uniformly with respect to X.As a result,observinguniformly with respect to X,we have
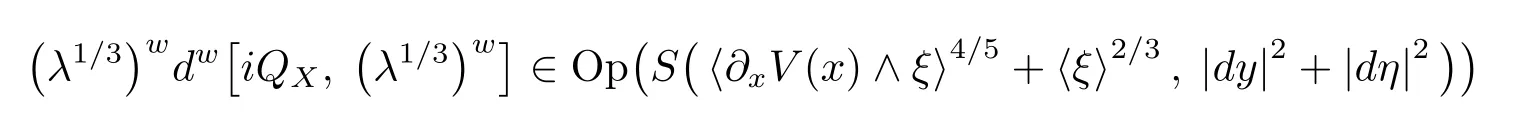
uniformly with respect to X,which implies
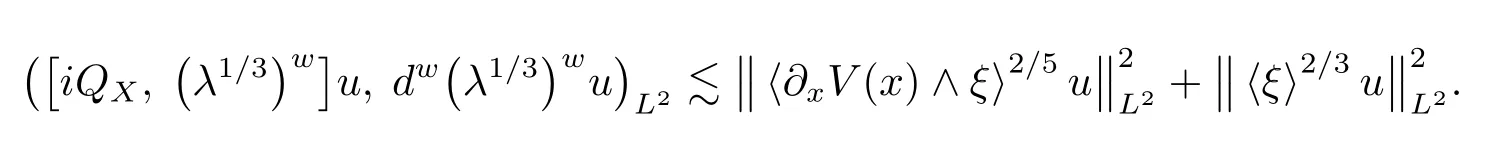
This along with(4.17)and(4.18)gives(4.15),since
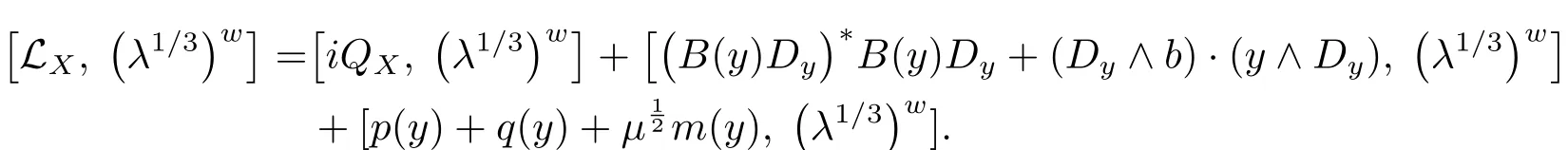
Next we prove(4.14).The relation
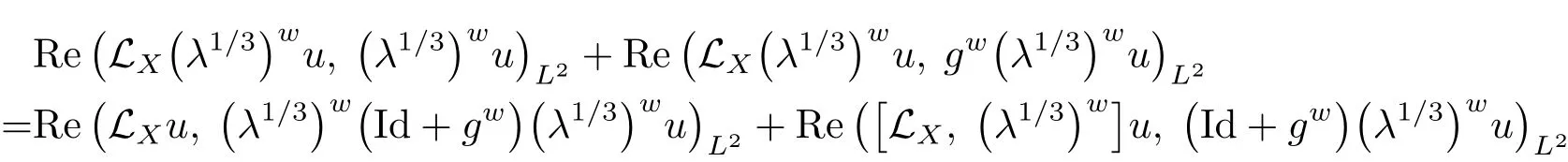
gives,with>0 arbitrary,
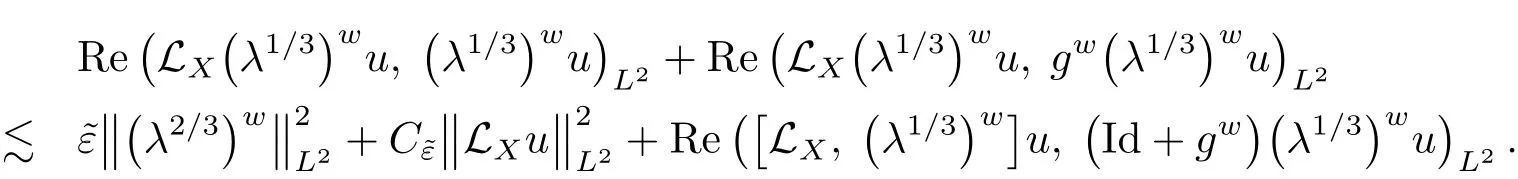
We could apply(4.15)with d=1+g to estimate the last term in the above inequality;this gives,with ε> 0 arbitrary,
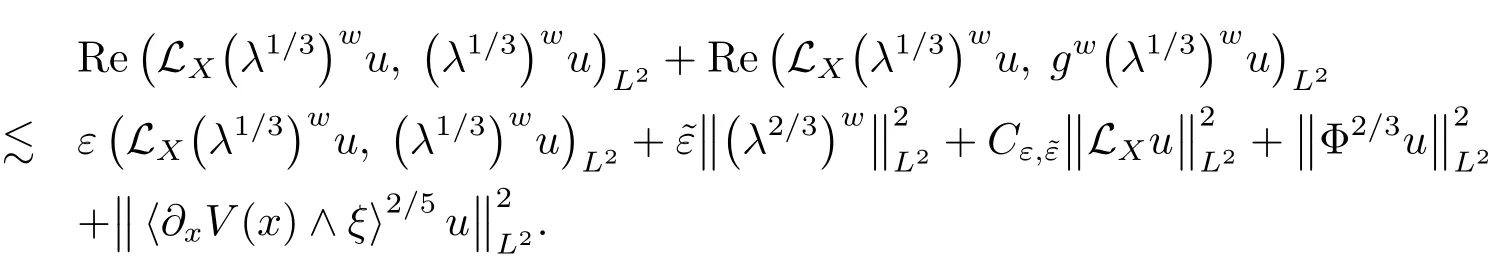
Let ε small enough yields the desired estimate(4.14).The proof is thus completed.
4.1 Proof of Proposition 4.1
In what follows,let hN,with N a large integer,be a symbol de fined by
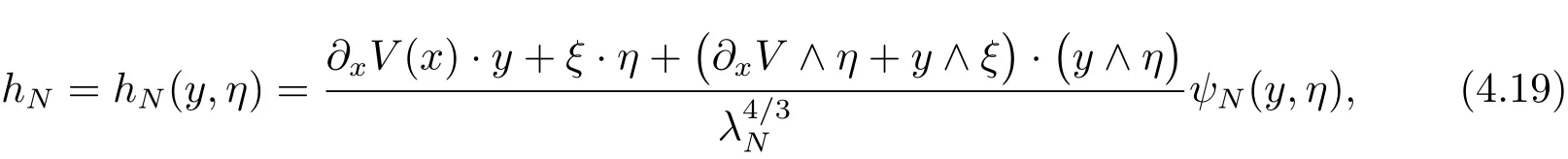
where

and
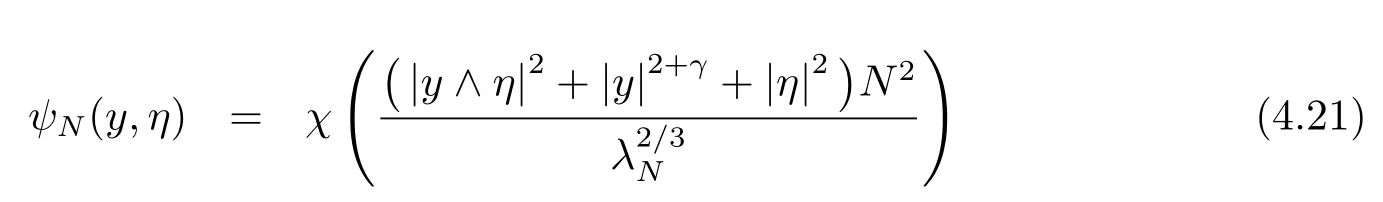
with χ ∈(R;[0,1])such that χ =1 in[?1,1]and supp χ ? [?2,2].
Lemma 4.5Let λNbe given in(4.20).Then

uniformly with respect to X.Moreover,if σ≤1,then
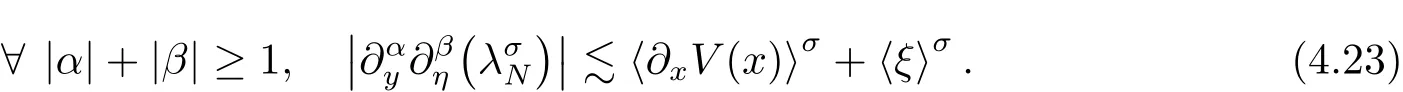
ProofThe proof is the same as Lemma 4.2.
Lemma 4.6The symbol hNgiven in(4.19)belongs to S(1,|dy|2+|dη|2)uniformly with respect to X.
Proofstraightforward calculatation to get
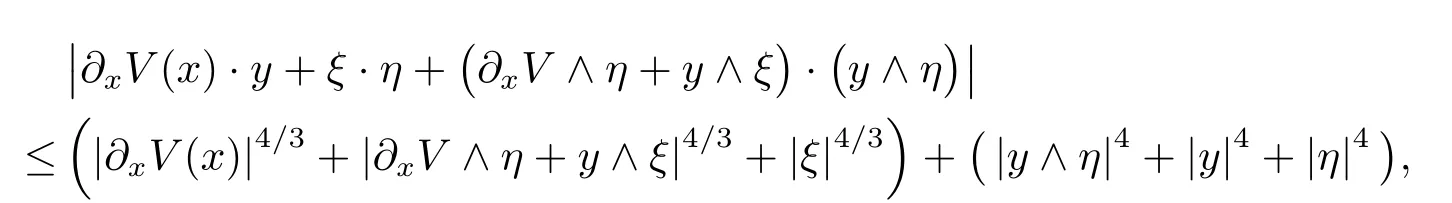
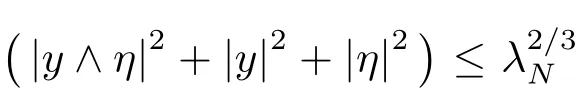
Lemma 4.7Let λNand ψNbe given in(4.20)and(4.21).Then for any σ ∈ R,the following two inequalities
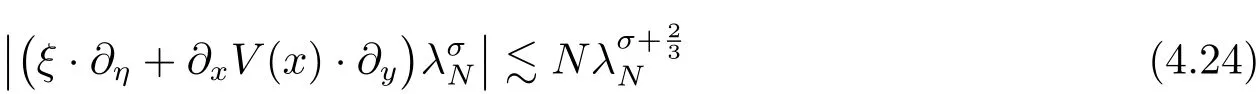
and
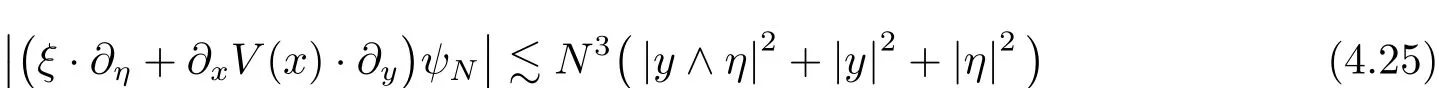
hold uniformly with respect to(x,ξ).



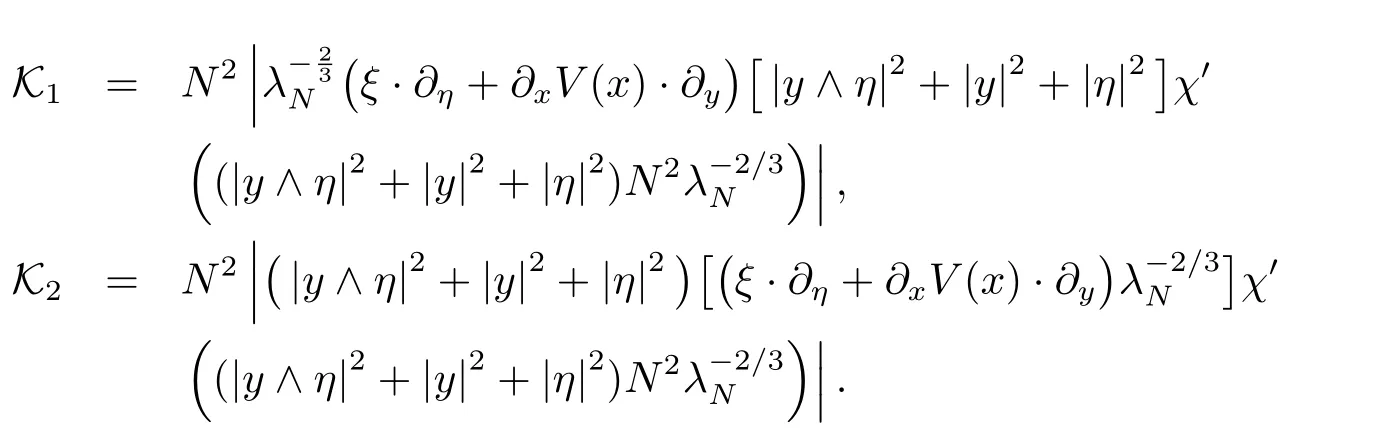
Using(4.24)showsMoreover direct computation givesthe last inequality following from the fact thaton the support of the functionthen the above inequalities yield the desired inequality(4.25).The proof of Lemma is thus completed.
The rest of this section is occupied by
Proof of Proposition 4.1Since the proof is quite long,we divide it into three steps.
Step ILet N be a large integer to be determined later andbe the Wick quantization of the symbol hNgiven in(4.19).To simplify the notation we will use CNto denote different suitable constants which depend only on N.In the following discussion,let u ∈ S().By(2.4)and Lemma 4.6,we can find a symbolsuch that H=withuniformly with respect to X.Then using Lemma 3.3,one gives
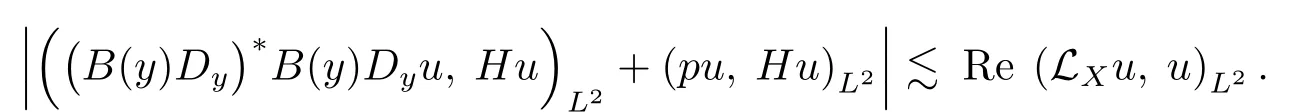
This together with the relation
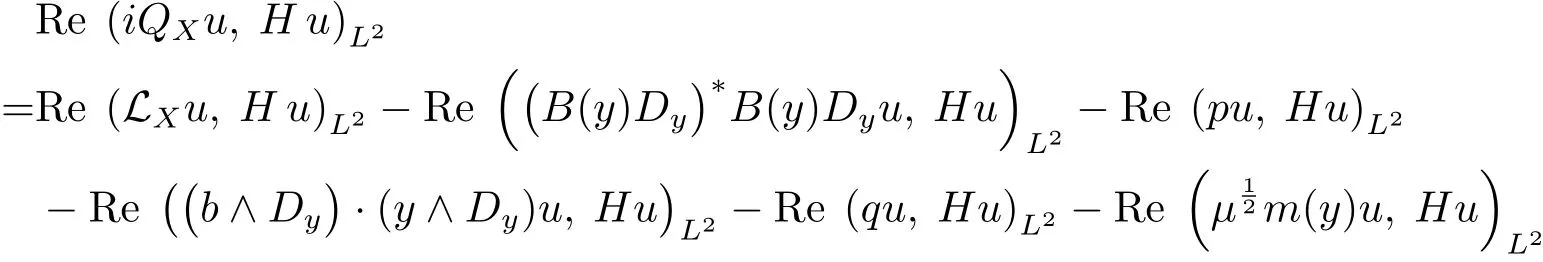
yields
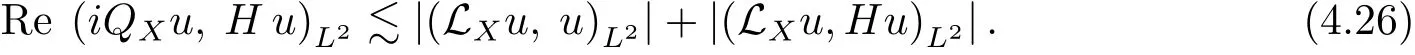
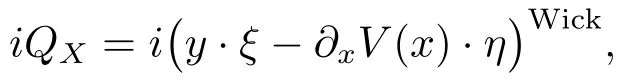
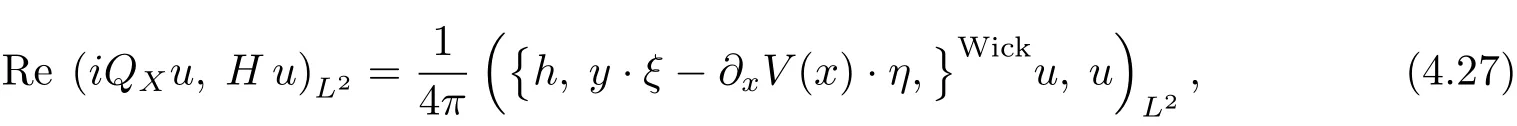
where{·, ·}is the Poisson bracket de fined in(2.5).Direct calculus shows
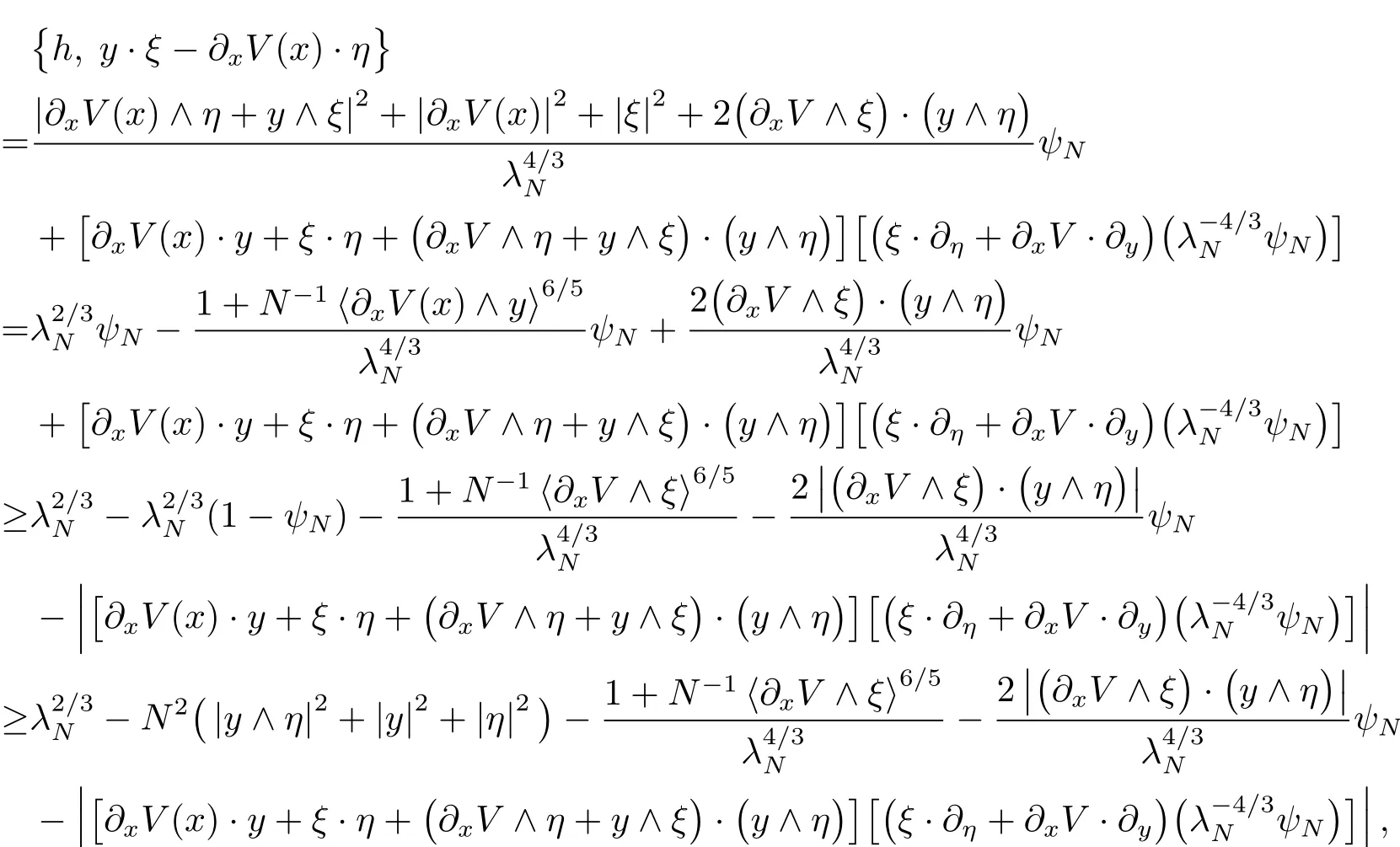
the last inequality holding becauseon the support of 1?ψN.Due to the positivity of the Wick quantization,the above inequalities,along with(4.26),(4.27)and the estimate
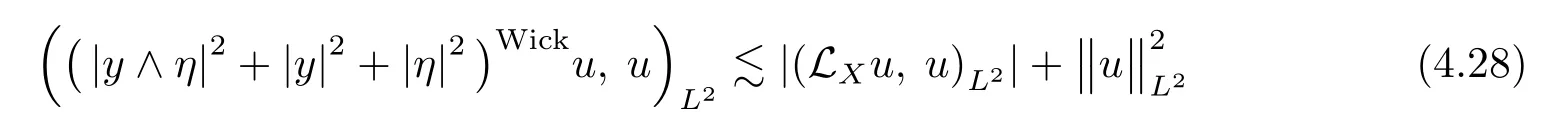
due to(4.9),yield

where Rjare given by
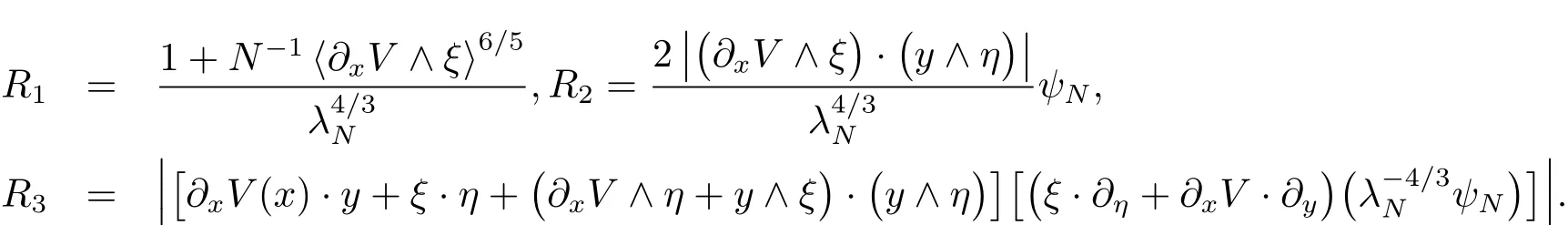
Step IIIn this step,we will treat the above terms Rj,and show that there exists a symbol q,belonging to S(1,|dy|2+|dη|2)uniformly with respect to X,such that
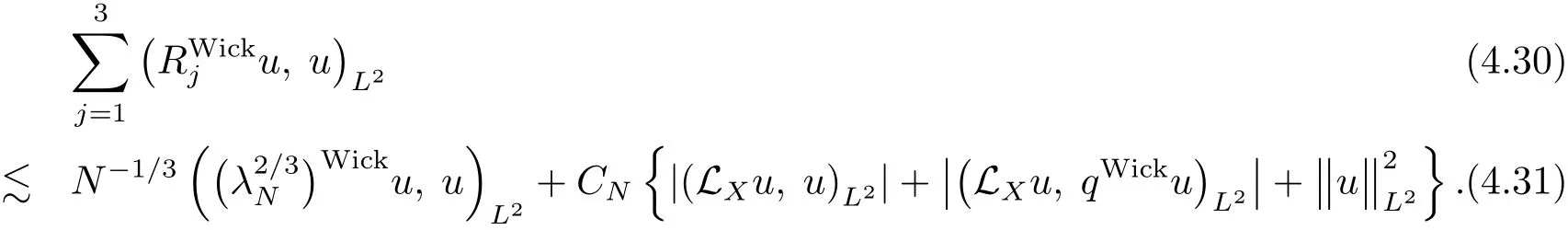
For this purpose,we de fine q by

with
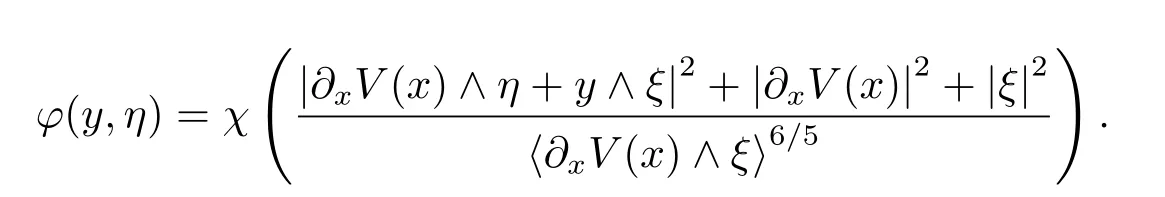
Then one can verify that q ∈ S(1,|dy|2+|dη|2)uniformly with respect to(x,ξ).Thus by(3.4),we conclude
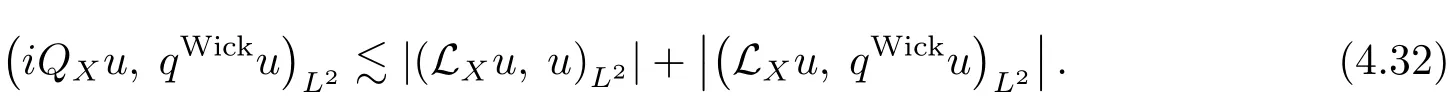
On the other hand,it is just a direct computation of the Poisson bracke to see that

with
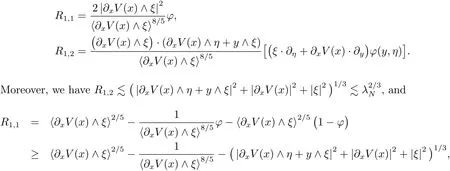
where the last inequality holds because
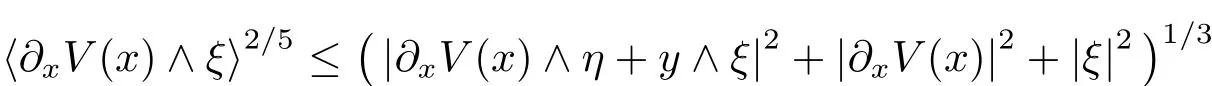
on the support of 1??.These inequalities,combining(4.33)and(4.32),yield
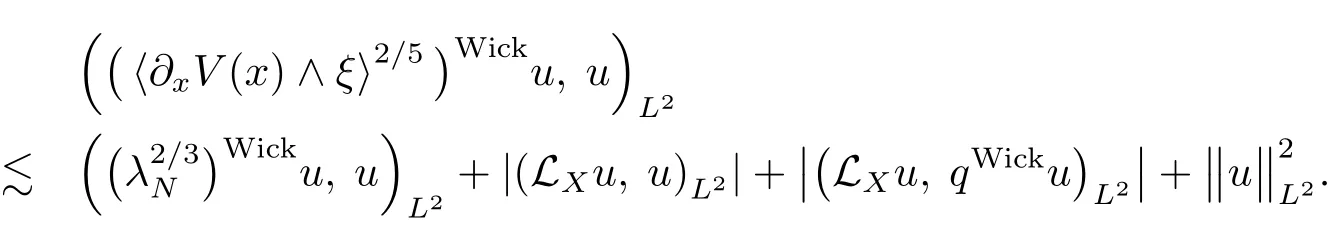
Consequently,observing that
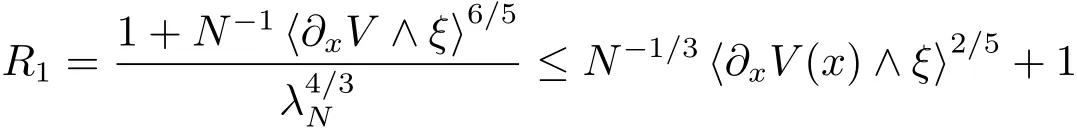
and
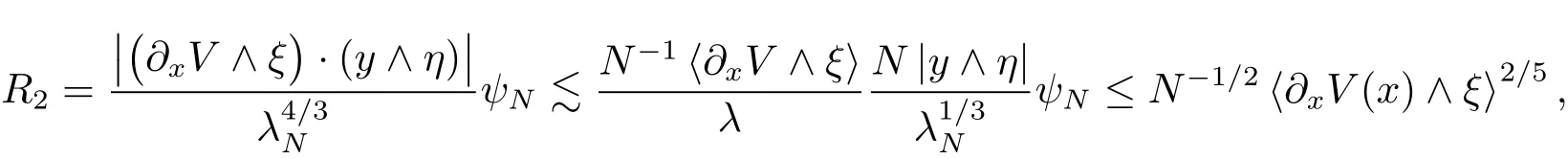
we get the desired upper bound for the terms R1and R2.It remains to handle R3.By virtue of(4.24)and(4.25),we compute
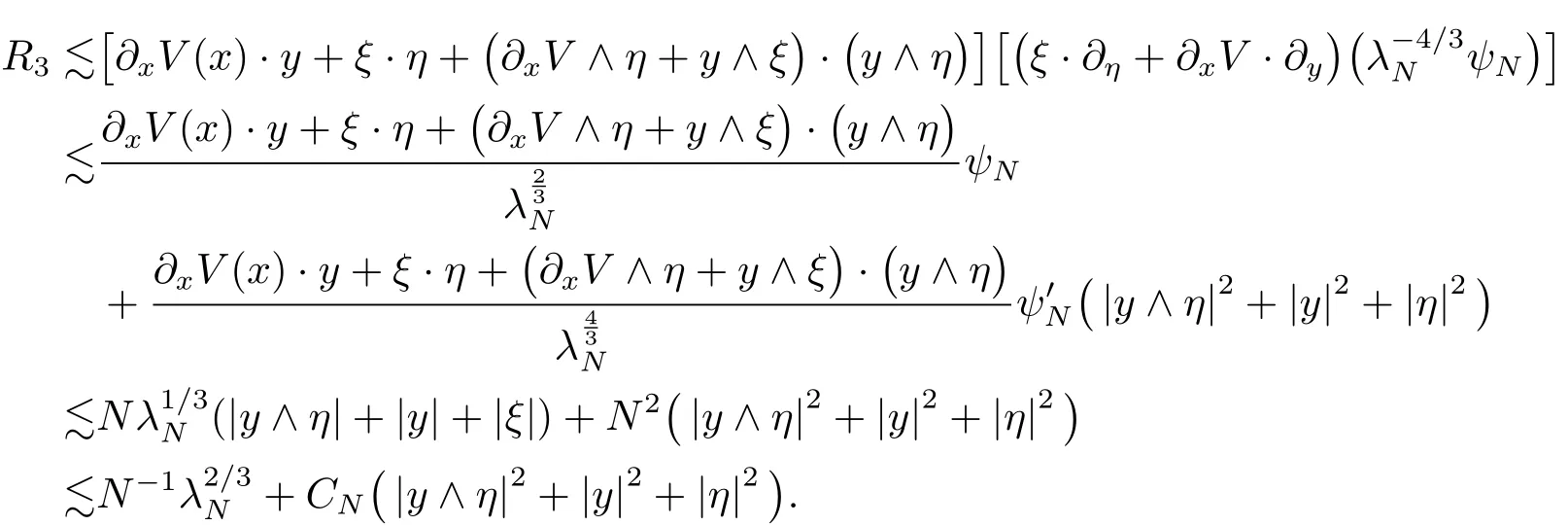
The forth inequlity result from
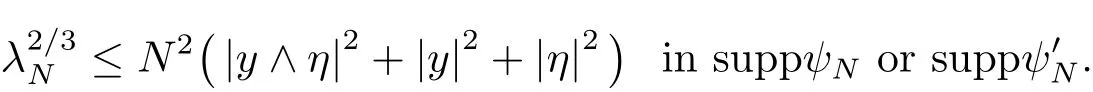
As a result,the positivity of Wick quantization gives
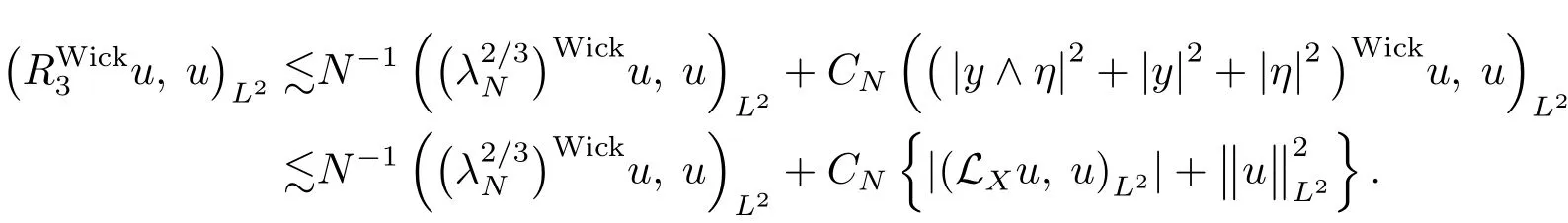
Thus the desired estimate(4.30)follows.
Step IIINow,we proceed the proof of Proposition 4.1.From(4.29)and(4.30),it follows that there exists a symbol p ∈ S(1,|dy|2+|dη|2)uniformly with respect to X,such that
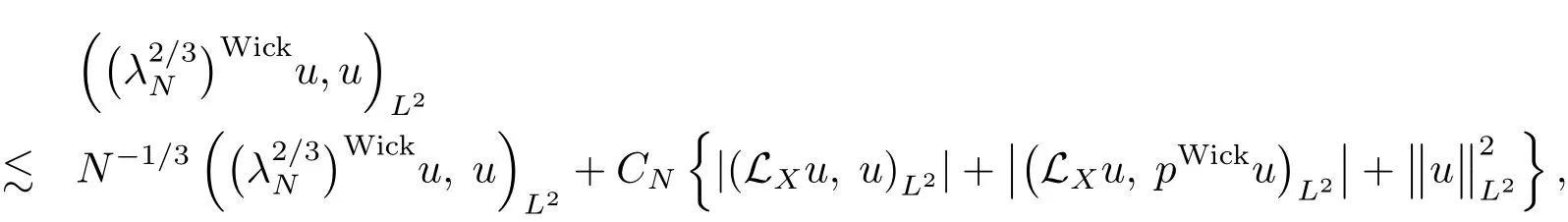
which allows us to choose an integer N0large enough,such that

Consequently,observing thatwith λ de fined in(4.2),we get,combining(4.28),
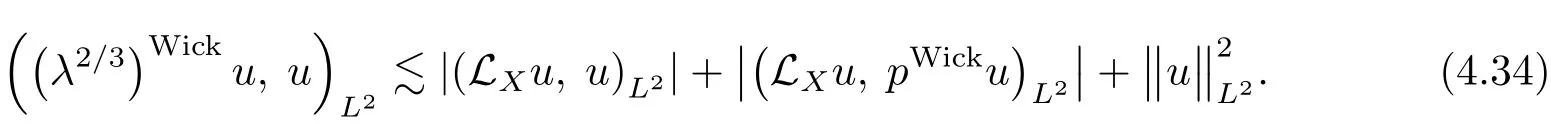
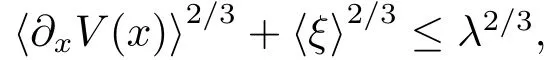
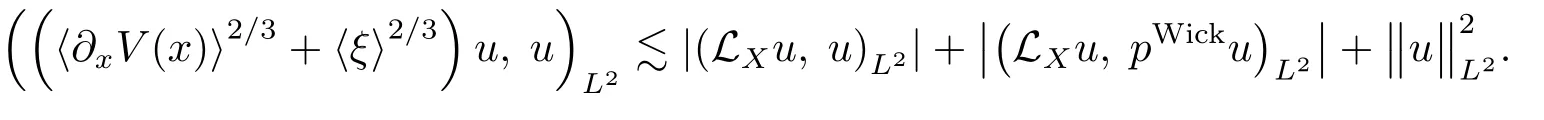
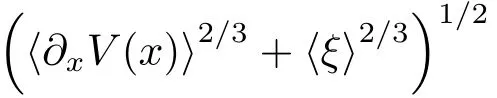

Similarly,since〈?xV(x)∧ ξ〉2/5≤ λ2/3,then by virtue of(4.34)we have,repeating the above arguments,
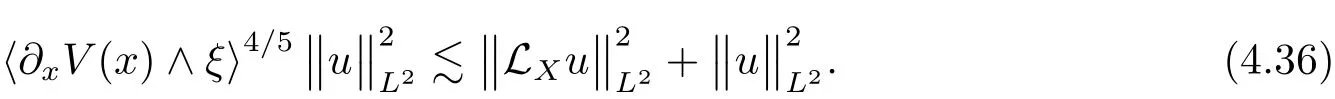
Now,we apply(4.34)to the functionto get
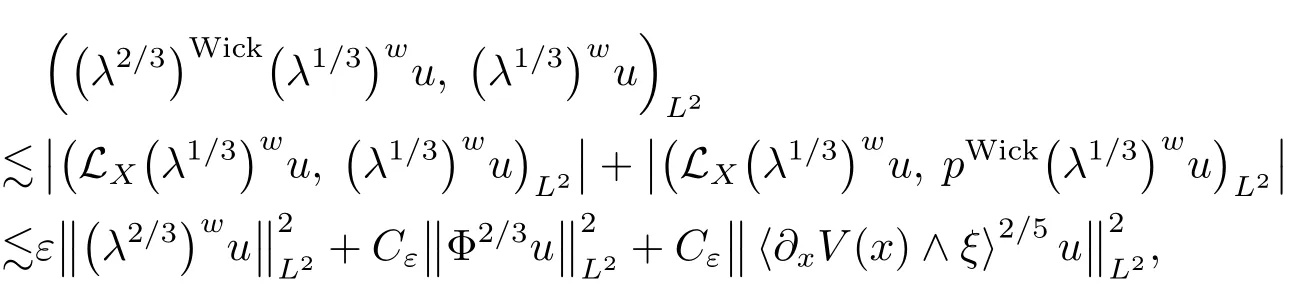
where the last inequality follows from(4.14).Furthermore,using(4.6)implies

Combining the above inequalities,we have
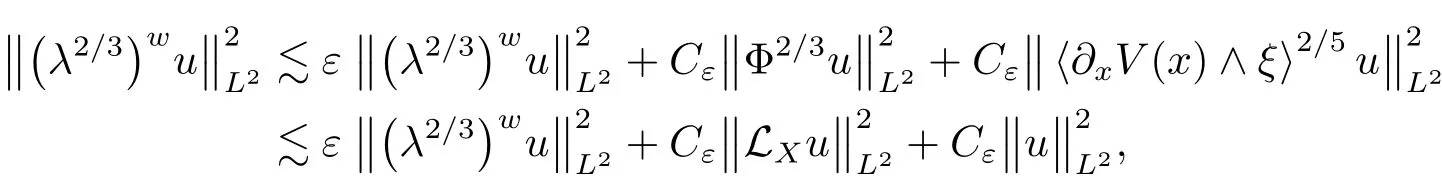
5 Proof of Theorem 1.1:Regularity Estimates in All Variables
In this section,we will show the hypoelliptic estimates in spatial and velocity variables for the original operator L.
Proposition 5.1Let V(x)be a C2-function satisfying assumption(1.8).Then for anyone has.
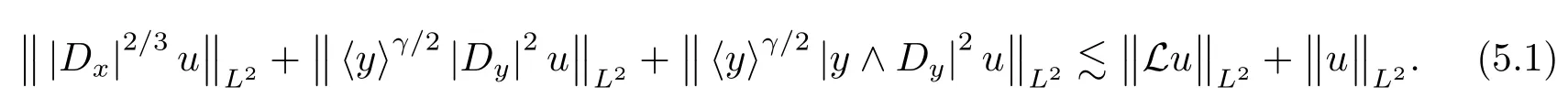
ProofThe proof of is quite similar as that of Proposition 4.1 in[2]and[3].So we only give a sketch here and refer to[2]and[3]for more detailed discussions.With each fixed xμ∈ R3,we associate an operator

Let PXμ,with Xμ=(xμ,ξ),be the operator de fined in(4.1),i.e.,
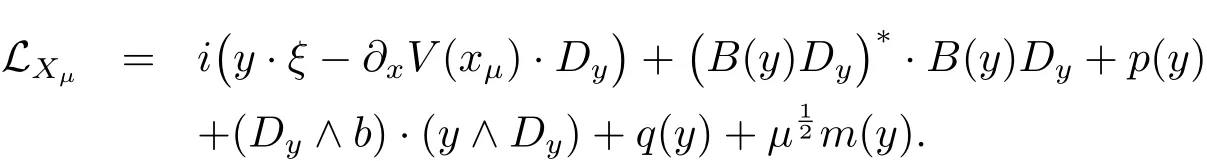
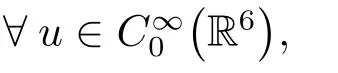

Lemma 4.2 in[1]shows the metric g de fined by gx= 〈?xV(x)〉2/3|dx|2,x ∈ R3is slowly varying,i.e.,we can find two constants C?,r0> 0 such that if gx(x?y)≤,then
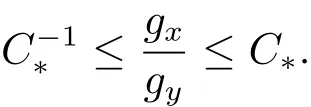
The main feature of a slowly varying metric is that it allows us to introduce some partitions of unity related to the metric(see for instance Lemma 18.4.4 of[8]).Precisely,we could find a constant r>0 and a sequence xμ∈Rn,μ≥ 1,such that the union of the balls
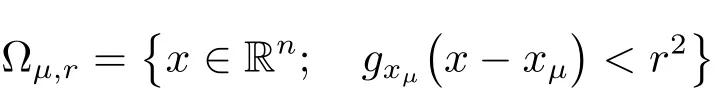
coves the whole space Rn.Moreover there exists a positive integer Nr,depending only on r,such that the intersection of more than Nrballs is always empty.One can choose a family of nonnegative functions{?μ}μ≥1in S(1,g)such that

Repeat the precess in[3],we see
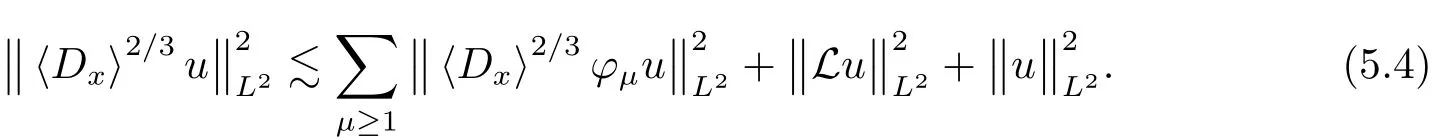
Using the notation

we may write ?μLu=Lxμ?μu+Rμu,then



Using(5.4)and(5.2),we have
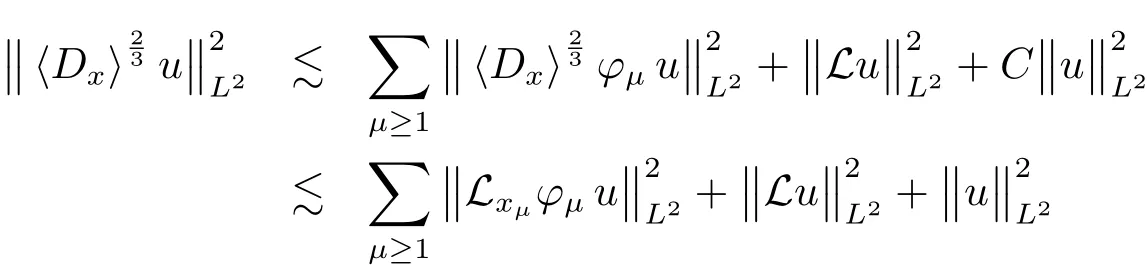
and

As a result,combining these inequalities gives(5.1).The proof is then completed.
References
[1]Li W X.Global Hypoellipticity and compactness of resolvent for Fokker-Planck operator[J].Ann.Sc.Norm.Super.Pisa Cl.Sci.,2012,XI:789–815.
[2]Li W X.Global hypoelliptic estimates for fractional order kinetic equation[J].Math.Nach.,2014,287:610–637.
[3]Fr′ed′eic H′erau,Li W X.Global hypoelliptic estimates for Landau-type operator with external potential[J].Kyoto J.Math.,2013,53:533–565.
[4]H′erau F,Pravda-Starov K.Anisotropic hypoelliptic estimates for Landau-type operators[J].J.Math.Pures et Appl.,2011,95:513–552.
[5]Lerner N,Morimoto Y,Pravda-Starov K,Xu C J.Phase space analysis and functional calculus for the linearized landau and boltzmann operators[J].Kinetic Rel.Mod.,2012,6(3):625–648.
[6]Desvillettes L,Villani C.On the spartially homogeneous Landau equation for hard potentials,part I:existence,uniqueness and smoothness[J].Comm.Part.Diff.Equ.,2000,25(1-2):179–259.
[7]H′erau F,Nier F.Isotropic hypoellipticity and trend to equilibrium for the Fokker-Planck equation with a high-degree potential[J].Arch.Ration.Mech.Anal.,2004,171(2):151–218,.
[8]H?rmander L.The analysis of partial differential equations[J].Berlin:Springer-Verlag,1985.
[9]Helffer B,Nier F.Hypoelliptic estimates and spectral theory for Fokker-Planck operators and Witten Laplacians[M].Lect.Notes Math.,Vol.1862,Berlin:Springer-Verlag,2005.
[10]Lerner N.The Wick calculus of pseudo-differential operators and some of its applications[J].Cubo Mat.Educ.,2003,5(1):213–236.
[11]Lerner N,Metrics on the phase space and non-selfadjoint pseudo-differential operators,Volume 3 of Pseudo-Differential Operators[M].Basel:Birkhuser Verlag,2010.
[12]Villani C.On the spatially homogeneous Landau equations for Maxwellian molecules[J].Math.Mod.Meth.Appl.Sci.,1998,8(6):957–983.
[13]Liu Zhenhai.Existence and uniqueness of solusions for nonlocal nonlinear evolution equations[J].J.Math.,1998,18(4):389–392.

