洪 勇, 溫雅敏

(廣東財(cái)經(jīng)大學(xué) 統(tǒng)計(jì)與數(shù)學(xué)學(xué)院, 廣州 510320)

1 引言與引理

設(shè)r>1,α是常數(shù), 定義函數(shù)空間

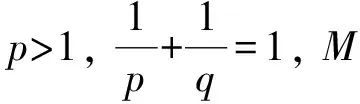
為Hilbert型積分不等式.

Hilbert型積分不等式在分析學(xué)及算子理論中應(yīng)用廣泛[1]. 當(dāng)積分核K(x,y)為齊次函數(shù)時(shí), 對(duì)Hilbert型不等式的研究已有很多結(jié)果[2-19]; 但當(dāng)K(x,y)為非齊次函數(shù)時(shí), 目前研究報(bào)道相對(duì)較少. 本文研究具有非齊次核的Hilbert型積分不等式成立的充要條件及其最佳常數(shù)因子.

設(shè)K(x,y)=G(xλ1yλ2)(λ1>0,λ2>0), 則顯然K(x,y)是一個(gè)非齊次函數(shù), 且對(duì)t>0滿足:

K(tx,y)=K(x,tλ1/λ2y),K(x,ty)=K(tλ2/λ1x,y).

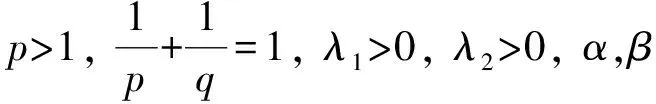
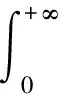
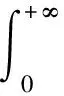
做變換xλ1/λ2y=t, 有

類似地可得ω2(y)=y(λ2/λ1)((α+1)/p-1)W2.

2 主要結(jié)果

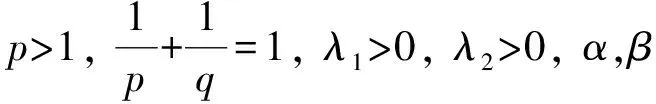
1) 存在常數(shù)M, 對(duì)一切f(x)∈Lp,α(0,+∞),g(y)∈Lq,β(0,+∞), 使Hilbert型不等式

(1)

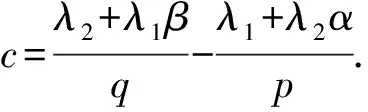
則有

(2)

同時(shí), 又有

由式(1)～(3), 得

(4)

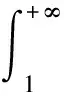
若c<0, 對(duì)足夠小的ε>0, 令

則類似地可得

(5)

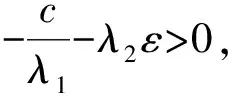
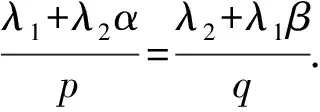
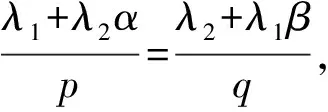
(6)

對(duì)足夠小的ε>0及δ>0, 取

則有

(7)

由式(6)～(8)得

令ε→0+, 得

再令δ→0+, 得

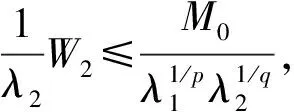
3 在算子理論中的應(yīng)用

設(shè)K(x,y)非負(fù)可測,f(x)∈Lr,α(0,+∞), 定義奇異積分算子T:

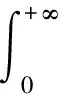
(9)

則T是一個(gè)線性算子. 若存在常數(shù)M, 使得?f(x)∈Lr,α(0,+∞), 有

‖T(f)‖r,γ≤M‖f‖r,α,

則稱T是從Lr,α(0,+∞)到Lr,γ(0,+∞)的有界線性算子. 此時(shí), 定義T的算子范數(shù)為

特別地, 當(dāng)T是從Lr,α(0,+∞)到自身的有界線性算子時(shí), 則稱T是Lr,α(0,+∞)中的有界線性算子.

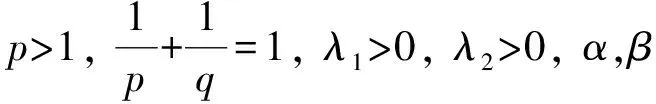
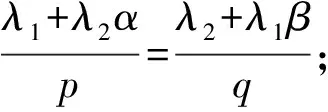
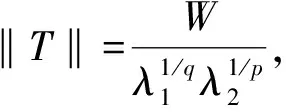
證明: 只需證明‖T(f)‖p,(1-p)β≤M‖f‖p,α與式(1)等價(jià)即可. 若式(1)成立, 令

則有

于是‖T(f)‖p,(1-p)β≤M‖f‖p,α.

反之, 若‖T(f)‖p,(1-p)β≤M‖f‖p,α, 則易得式(1), 因而式(1)與‖T(f)‖p,(1-p)β≤M‖f‖p,α等價(jià). 證畢.

在定理2中, 取α=β=0, 則可得到以下推論.

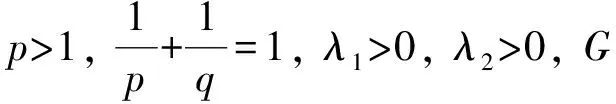
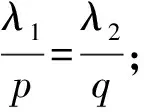
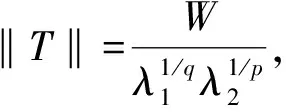
則:

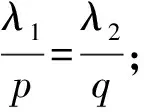
2) 若T是Lp(0,+∞)中的有界線性算子, 則T的范數(shù)

其中B(·,·)是Beta函數(shù).

同理

根據(jù)推論1知定理3成立.

[1] Hardy G H, Littlewood J E, Pólya G. Inequalities [M]. 2nd ed. Cambridge: Cambridge University Press, 1952.

[2] 和炳, 曹俊飛, 楊必成. 一個(gè)全新的多重Hilbert型積分不等式 [J]. 數(shù)學(xué)學(xué)報(bào)(中文版), 2015, 58(4): 661-672. (HE Bing, CAO Junfei, YANG Bicheng. A Brand New Multiple Hilbert-Type Integral Inequality [J]. Acta Mathematics Sinica (Chinese Series), 2015, 58(4): 661-672.)

[3] 洪勇. 一類具有準(zhǔn)齊次核的涉及多個(gè)函數(shù)的Hilbert型積分不等式 [J]. 數(shù)學(xué)學(xué)報(bào)(中文版), 2014, 57(5): 833-840. (HONG Yong. A Hilbert-Type Integral Inequality with Quasi-homoeneous Kernel and Several Functions [J]. Acta Mathematics Sinica (Chinese Series), 2014, 57(5): 833-840.)

[5] ZHONG Wuyi, YANG Bicheng. On a Multiple Hilbert-Type Integral Inequality with the Symmetric Kernel [J/OL]. J Inequal Appl, 2007-11-13. https://doi.org/10.1155/2007/27962.

[6] XIN Dongmei, YANG Bicheng, CHEN Qiang. A Discrete Hilbert-Type Inequality in the Whole Plane [J/OL]. J Inequal Appl, 2016-05-05. https://link.springer.com/article/10.1186/s13660-016-1075-3.

[7] 匡繼昌. 常用不等式 [M]. 濟(jì)南: 山東科學(xué)技術(shù)出版社, 2004. (KUANG Jichang. Applied Inequalities [M]. Jinan: Shangdong Science and Technology Press, 2004.)

[8] YANG Bicheng, CHEN Qiang. On a Hardy-Hilbert-Type Inequality with Paremeters [J/OL]. J Inequal Appl, 2015-10-24. https://link.springer.com/article/10.1186/s13660-015-0861-7.

[9] YANG Bicheng, CHEN Qiang. A New Extension of Hardy-Hilbert’s Inequality in the Whole Plane [J/OL]. J Funct Spaces, 2016-06-30. http://dx.doi.org/10.1155/2016/9197476.

[10] YANG Bicheng. On an Extension of Hilbert’s Integral Inequality with Some Parameters [J]. Aust J Math Anal Appl, 2004, 1(1): 1-8.

[11] Rassias M Th, YANG Bicheng. On a Hardy-Hilbert-Type Inequality with a General Homogeneous Kernel [J]. Int J Nonlinear Anal Appl, 2015, 7(1): 249-269.

[12] CHEN Qiang, SHI Yanping, YANG Bicheng. A Relation between Two Simple Hardy-Mulholland-Type Inequalities with Parameters [J/OL]. J Inequal Appl, 2016-02-24. https://link.springer.com/article/10.1186/s13660-016-1020-5.

[13] 洪勇, 溫雅敏. 齊次核的Hilbert型級(jí)數(shù)不等式取最佳常數(shù)因子的充要條件 [J]. 數(shù)學(xué)年刊(中文版), 2016, 37A(3): 329-336. (HONG Yong, WEN Yamin. A Necessary and Sufficient Condition of That Hilbert Type Series Inequality with Homogeneous Kernel Has the Best Constant Factor [J]. Chinese Annals of Mathematics, 2016, 37A(3): 329-336.)

[14] YANG Bicheng, CHEN Qiang. On a More Accurate Hardy-Mulholland-Type Inequality [J/OL]. J Inequal Appl, 2016-03-02. https://link.springer.com/article/10.1186/s13660-016-1026-z.

[15] GAO Mingzhe, YANG Bicheng. On the Extended Hilbert’s Inequality [J]. Proc Amer Math Soc, 1998, 126(3): 751-759.

[16] YANG Bicheng. On a More Accurate Multidimensional Hilbrt-Type Inequality with Parameters [J]. Math Inequal Appl, 2015, 18(2): 429-441.

[17] HONG Yong. On Multiple Hardy-Hilbert Integral Inequalities with Some Parameters [J/OL]. J Inequal Appl, 2006-09-20. https://link.springer.com/article/10.1155/JIA/2006/94960.

[18] HUANG Qiliang, YANG Bicheng. On a Multiple Hilbert-Type Integral Operator and Applications [J/OL]. J Inequal Appl, 2009-12-09. https://doi.org/10.1155/2009/192197.

[19] 楊必成. 算子范數(shù)與Hilbert型不等式 [M]. 北京: 科學(xué)出版社, 2009. (YANG Bicheng. The Norm of Operator and Hilbert-Type Inequalities [M]. Beijing: Science Press, 2009.)