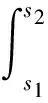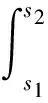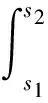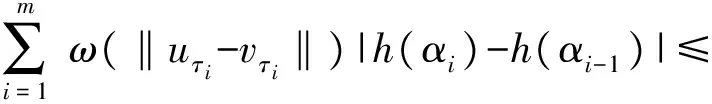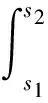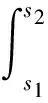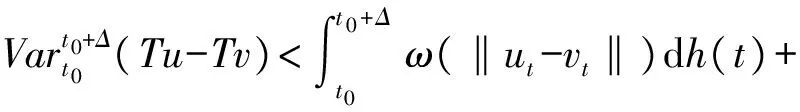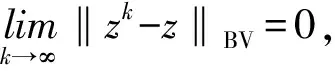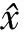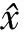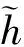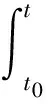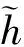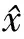滯后型脈沖微分方程的有界變差解
李寶麟, 安曉偉, 茍海德
(西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院, 甘肅 蘭州 730070)
Henstock-Kurzweil積分包含了Riemann積分和Lebesgue積分[1],這類積分的一個典型特征是如F′(t)這樣的高振動函數(shù)的積分可以定義,其中F(t)=t2sin t-2,t∈(0,1],F(0)=0.Henstock等[2]于1957—1958年建立的Henstock-Kurzweil積分在常微分方程問題研究中有很好的應(yīng)用.李寶麟等[3]借助Henstock-Kurzweil積分研究了一類滯后型泛函微分方程
的有界變差解的存在性.本文在文獻[3]的基礎(chǔ)上,借助Henstock-Kurzweil積分,考慮滯后型脈沖微分方程
(1)
的有界變差解的存在性,其中t0∈R,r≥0,σ≥0,x∈Rn表示定義在[t0-r,t0+σ]上的函數(shù).對任意的t∈[t0,t0+σ],定義函數(shù)xt(θ)=x(t+θ),θ∈[-r,0],Ik:Rn→Rn連續(xù),k=1,2,…,m,t0 (2) 本文假定滯后型脈沖微分方程的右端函數(shù)所滿足的條件比文獻[4-6]更為廣泛,假定被積函數(shù)f是Henstock-Kurzweil可積的,且φ是正則函數(shù). 引理1.2[6]如果u在[a,b]上Lebesgue可積,則它在[a,b]上H-K可積. 引理1.3[6]如果u在[a,b]上是非負(fù)的且H-K可積,則它在[a,b]上Lebesgue可積. 定理1.4設(shè)u,um:[a,b]→Rn,m=1,2,…,其中{um}在[a,b]上H-K可積.如果: (i) 存在正值函數(shù)δ:[a,b]→R+,使得對任意的ε>0,存在P:[a,b]→N及定義在閉區(qū)間J?[a,b]上的正值超可加區(qū)間函數(shù)Φ:J?[a,b]→R+,滿足Φ([a,b])<ε,使得對每個τ∈[a,b]及δ-精細區(qū)間[τ,j],τ∈J,當(dāng)m>P(τ)時,有 ‖(um(τ)-u(τ))|J|‖≤Φ(J); (3) (4) 則稱u在[a,b]上H-K可積,且 (5) 證明易知Rn-值函數(shù)是收斂的當(dāng)且僅當(dāng)它的每個分量都收斂.因此,不失一般性,僅考慮實值函數(shù)序列.設(shè)u是一個實值函數(shù),由(3)式有 |(um(τ)-u(τ))|J||≤Φ(J). 再由文獻[8]的定理1.29,結(jié)論成立. 本章主要回顧滯后型脈沖微分方程及相關(guān)的結(jié)果. 顯然,當(dāng)函數(shù)x∈G-([t0-r,t0+σ],Rn)時,對任意的t∈[t0,t0+σ]都有xt∈G-([-r,0],Rn). 令H1?G-([-r,0],Rn),{xt|t∈[t0,t0+σ],x∈G1}?H1,假設(shè)f(t,xt):(t,xt)∈[t0,t0+σ]×G-([-r,0],Rn)滿足以下條件: (A) 存在正值函數(shù)δ(τ):[t0,t0+σ]→R+,使得對每個區(qū)間[u,v]滿足τ∈[u,v]?(τ-δ(τ),τ+δ(τ))?[t0,t0+σ]及x∈G1,都有 ‖f(τ,xτ)(v-u)‖≤|h(v)-h(u)|; (B) 對每個區(qū)間[u,v]滿足τ∈[u,v]?(τ-δ(τ),τ+δ(τ))?[t0,t0+σ]及x,y∈G1,都有 ‖f(τ,xτ)-f(τ,yτ)‖(v-u)≤ 其中,h:[t0,t0+σ]→R是不減的左連續(xù)函數(shù),ω:[0,∞)→R是連續(xù)的增函數(shù),且ω(r)=r,r≥0. 定義2.1設(shè)Ω?[t0,t0+σ]×H1是開集,若函數(shù)f:Ω→Rn是Carathéodory函數(shù),如果f滿足條件(A)和(B),則f∈H(Ω,h,ω). 證明設(shè)ε>0給定,由條件(B),對每個τ∈[α,β]?[t0,t0+σ],t1≤τ≤t2,[t1,t2]?[α,β],有 ‖f(τ,(xk)τ)-f(τ,xτ)‖(t2-t1)≤ (6) 令 函數(shù)μ:[α,β]→R是不減的且μ(β)-μ(α)<ε,因此 由于對每個t∈[α,β],函數(shù)ω在0處連續(xù),則存在p(τ)∈N,使得對k≥p(τ),有 令Φ(J)=μ(t2)-μ(t1),J=[t1,t2],對k≥p(τ),不等式(6)可寫為形式 其中τ∈J?(τ-δ(τ),τ+δ(τ))?[α,β]. S={x∈Rn:‖x‖ (7) 證明由于每個有界變差函數(shù)都是有限階梯函數(shù)的一致極限[9],由推論2.3,結(jié)論成立. (8) 成立. 由ε>0的任意性有 下面考慮方程(2)的脈沖項,對脈沖函數(shù)Ik:Rn→Rn,k=1,2,…,n,假設(shè)以下條件成立. (C) 存在一個常數(shù)K>0,使得對所有的k=1,2,…,n及x,y∈Rn,有 Ik(x)-Ik(y)≤K|x-y|. 給定一個d∈[t0,t0+σ],定義 則 且方程(2)等價于 定義3.1[10]x(t,t0,x0),t∈[t0,T]?[a,b]是滯后型脈沖微分方程(1)的解,如果: (ii)x(t)在[t0,T]上的任意緊子區(qū)間是有界變差的; (iii) 對t∈[t0,T],有(x,t)∈G; (v)Δ(t)|t=tk=x(tk+)-x(tk)=Ik(x(tk)),tk∈[t0,T]. 定理3.2設(shè)f∈H(Ω,h,ω).如果x:[α,β]→Rn,[α,β]?[t0-r,t0+σ]是方程(6)的一個解,則x在[α,β]上有界變差且 證明令α=t0 引理3.3設(shè)X是Banach空間,U是X中的有界閉凸集,T:U→U連續(xù)且T(U)列緊,則T在U上必有一個不動點. 定理3.4設(shè)φ是H1上的函數(shù),f∈H(Ω,h,ω),Ik:Rn→Rn滿足條件(C),且對θ1,θ2∈[-r,0],有 ‖φ(θ1)-φ(θ2)‖≤|h(θ1)-h(θ2)|, (10) 則對每個(t0,φ)∈Ω,存在Δ>0,使得方程(2)在區(qū)間[t0-r,t0+Δ]?[t0-r,t0+σ]上存在解 G-([t0-r,t0+Δ],Rn). 證明考慮以下2種情形:函數(shù)h:[t0,t0+σ]→R在點t0處連續(xù)及不連續(xù). 首先,設(shè)函數(shù)h在點t0處連續(xù),即有h(t0+)=h(t0).由于G1是開集,則存在Δ>0,使得對任意的t∈[t0,t0+Δ]?[t0,t0+σ]及x∈Rn有 ‖x(t)-φ(0)‖=‖x(t)-x(t0+)‖< ‖z-φ(0)‖≤‖zk-z‖+‖zk-φ(0)‖<ε+b, 即有 ‖z-φ(0)‖≤b. 類似地,對每個t∈[t0,t0+Δ]有 從而,對任意的ε>0及t∈[t0,t0+Δ],當(dāng)k∈N充分大時有 即有 其中, h(t)=h1(t)+h2(t), 其中θ1=s-t0∈[-r,0].令 b=max{|h(t0+Δ)-h(t0)|, |h(θ1)-h(θ)|}, (11) 取t0≤s1 和 因此 由ε>0的任意性有 及 (13) 從而由函數(shù)ω1=ω(r)+K在0處連續(xù),且ω1(0)=0,有 從而由(13)式有 再由(11)式有 另一方面,對t∈[t0-r,t0]有 (Tzk)(t)=φ(t-t0)=(Tz)(t), 則Tzk→Tz(k→∞),即T是連續(xù)映射. 最后,證明T(Q)?Q在Banach空間BV([t0-r,t0+Δ],Rn)是序列緊的. 由(8)式有y∈BV-([t0-r,t0+Δ],Rn),且易證 從而T是序列緊的. 下面考慮函數(shù)h在點t0處不連續(xù).定義 類似于上一種情形,存在Δ>0,使得對t∈[t0,t0+Δ]?[t0,t0+σ]及x∈Rn,(t,xt)∈Ω,有 G-([t0-r,t0+Δ],Rn). [1] LEE P Y. Lectures on Henstock Integration[M]. Singapore:World Scientific,1989. [2] KURZWEIL J. Generalized ordinary differential equations and continuous dependence on a parameter[J]. Czech Math J,1957,7(82):418-449. [3] 李寶麟,茍海德. 滯后型泛函微分方程的有界變差解[J]. 數(shù)學(xué)雜志,2015,35(3):567-578. [4] FEDERSON M, SCHWABIK S. Generalized ODE approach to impulsive retarded functional differential equations[J]. Diff Integ Eqns,2006,19(11):1201-1234. [5] WU C X, LI B L. Bounded variation solution for discontinuous systems[J]. J Math Study,1998,31(4):417-427. [6] 傅希林,閆寶強,劉衍勝. 脈沖微分系統(tǒng)引論[M]. 北京:科學(xué)出版社,2005. [7] FEDERSON M, T′ABOAS P Z. Topological dynamics of retarded functional differential equations[J]. J Diff Eqns,2003,195(2):313-331. [8] SCHWABIK S. Generalized Ordinary Differential Equations[M]. Singapore:World Scientifc,1992. [9] SCHWABIK S, TVRD′Y M. Boundary value problems for generalized linear differential equations[J]. Czech Math J,1979,29(3):451-477. [10] 李寶麟,梁雪峰. 一類脈沖微分系統(tǒng)的有界變差解[J]. 西北師范大學(xué)學(xué)報(自然科學(xué)版),2007,41(4):192-198. [11] FEDERSON M. Converse Lyapunov theorems for retarded functional differential equations[J]. Cadernos de Matematica,2007,8(1):285-303. [12] PURNA C D, RISHI R S. Existence and stability of measure differential equations[J]. Czechoslovak Math J,1972,22(97):145-158. [13] HINO Y, MURAKAMI S, NAITO T. Functional Differential Equations with Infinite Delay[M]. New York:Springer-Verlag,1991. [14] KURZWEIL J. Generalized ordinary differential equations[J]. Czechoslovak Math J,1958,83(8):360-389. [15] 朱雯雯,徐有基. 帶非線性邊界條件的一階微分方程多個正解的存在性[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2016,39(2):226-230. [16] SLAVIK A. Well-posedness results for abstract generalized differential equations and measure functional differential equations[J]. J Math Anal Appl,2015,259(2):666-707. [17] FEDERSON M, GRAU R, MESQUITA J G, et al. Boundedness of solutions of measure differential equations and dynamic equations on time scales[J]. J Diff Eqns,2017,263(1):26-56.1 Henstock-Kurzweil積分
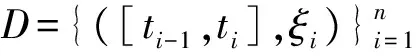
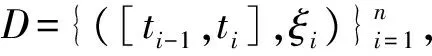

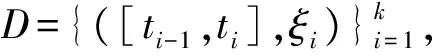

2 滯后型脈沖微分方程
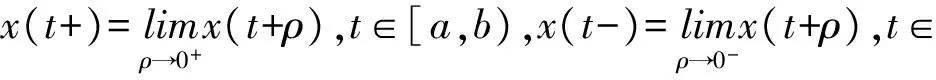
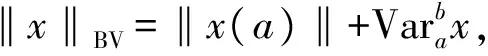
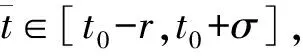
ω(‖xτ-yτ‖)|h(v)-h(u)|,
ω(‖(xk)τ-xτ‖)(h(t2)-h(t1)).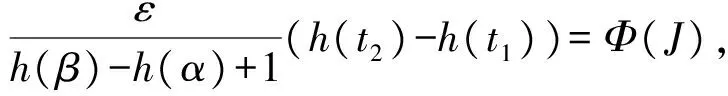
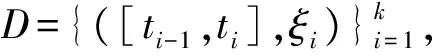
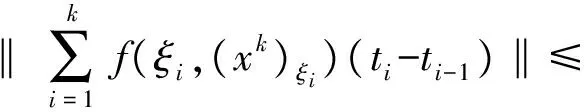





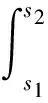

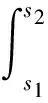
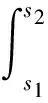
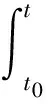
3 有界變差解的存在性
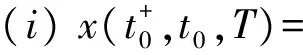


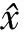
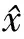
|h(t)-h(t0)|, (t,xt)∈Ω.