安徽省無為縣牛埠中學(xué)(238351) 朱小扣

對(duì)學(xué)生的空間想能力的考察一直是高考的重點(diǎn),其中也不乏有對(duì)多面體各個(gè)面延伸的考察,如2013高考數(shù)學(xué)江西卷理科第8題等.在平時(shí),同學(xué)們也能掌握三棱柱各個(gè)面延伸分空間21個(gè)部分,正方體各個(gè)面延伸分空間27個(gè)部分及其他棱柱的情形,但對(duì)于正棱錐與正棱臺(tái).大多數(shù)同學(xué)都不太清楚,筆者翻遍數(shù)學(xué)資料,發(fā)現(xiàn)對(duì)此問題的討論寥若晨星.筆者現(xiàn)將對(duì)正偶棱錐與正偶棱臺(tái)延伸問題的探究寫成此文,以饗讀者.為了解決此類問題,現(xiàn)對(duì)讀者熟悉的三棱錐(臺(tái))的情形進(jìn)行討論.

1.從簡出發(fā),探究思路

1.1 探討三棱錐各個(gè)面延伸可以把空間分成多少個(gè)部分?三棱臺(tái)各個(gè)面延伸可以把空間分成多少個(gè)部分?

解

(1)如圖1,現(xiàn)將三棱錐O?ABC特殊成OA,OB,OC互相垂直,將其放在如上圖的位置,8個(gè)卦限中,只有第七卦限沒有被平面一分為二,其他的卦限都一分為二了,故有8+7=15個(gè),類似的可以得到普通的三棱錐也是15個(gè).

(2)如圖2,類似第一問的解答,將三棱臺(tái)ABC?A1B1C1放在如圖2的位置,易知答案為:7+7+8=22

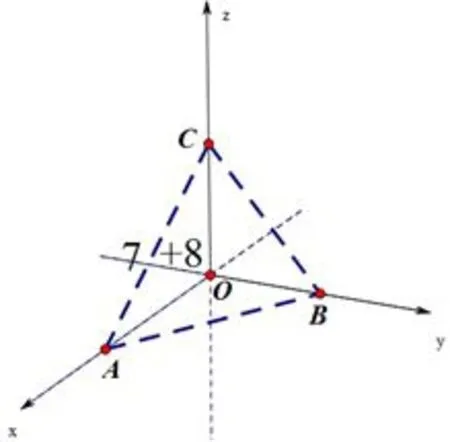
圖1

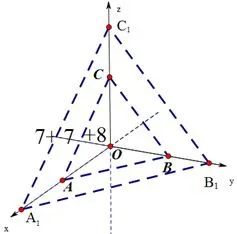
圖2

1.2 啟發(fā)

這樣做能很好的理解延伸三棱錐(臺(tái))各個(gè)面延伸分空間成多少個(gè)部分這一問題,可以彌補(bǔ)了空間想象力的不足.由此,我們可以得到解決此類問題策略:借助模型和降維處理.我們將用它解決正n(n為偶數(shù))棱錐(臺(tái))的情形.

2.化繁為簡,拾級(jí)而上

直接做正棱錐各個(gè)面延伸可以把空間分成多少個(gè)部分這一問題,非常困難.故我們先規(guī)定向上的是側(cè)棱延伸,不是側(cè)面延伸,進(jìn)行探討(為了方便敘述,規(guī)定:本文中出現(xiàn)的各棱延伸均指側(cè)棱向上延伸,向下是指面延伸).

2.1 正四棱錐各棱延伸可以把空間分成多少個(gè)部分?

解

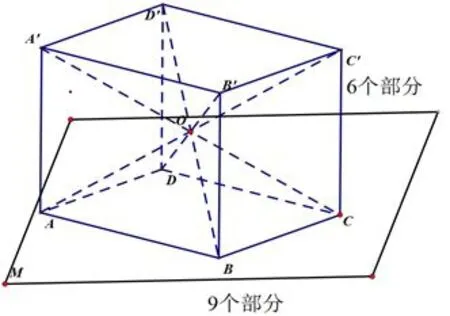
圖3

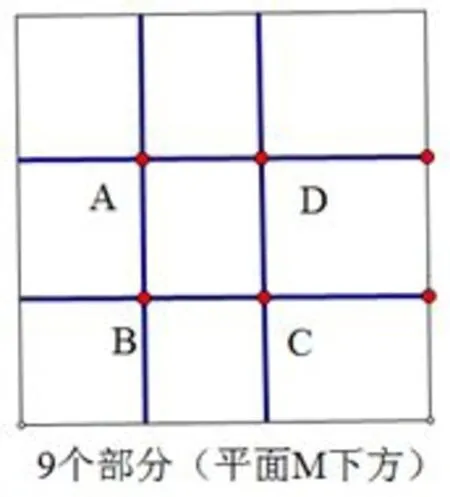
圖4

如圖3,圖4,可以將四棱錐O?ABCD各棱向上延伸得到長方體ABCD?A′B′C′D′.于是,平面M上方有O?ABCD,O?ABB′A′,O?BCC′B′,O?CDD′C′,O?DAA′D′,O?A′B′C′D′共6個(gè)部分,平面M下方9個(gè)部分,共15個(gè).

2.2 正四棱臺(tái)各棱可以把空間分成多少個(gè)部分?

解

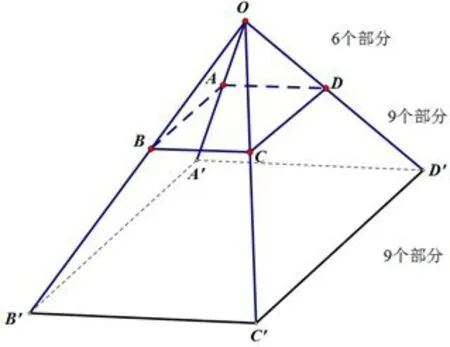
圖5

如圖5可以將正四棱臺(tái)ABCD?A′B′C′D′的各棱延伸就得到了四棱錐O?ABCD,類比四棱錐,有6+9+9=24,共24個(gè)部分.

2.3 正六棱錐各棱延伸可以把空間分成多少個(gè)部分?

解

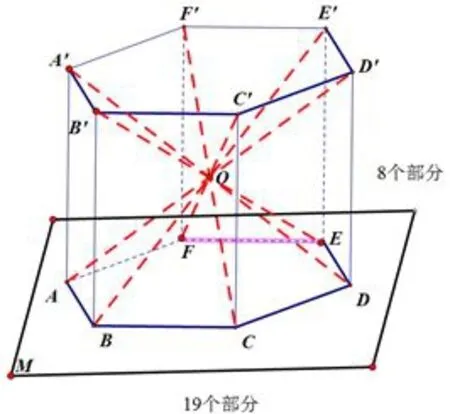
圖6

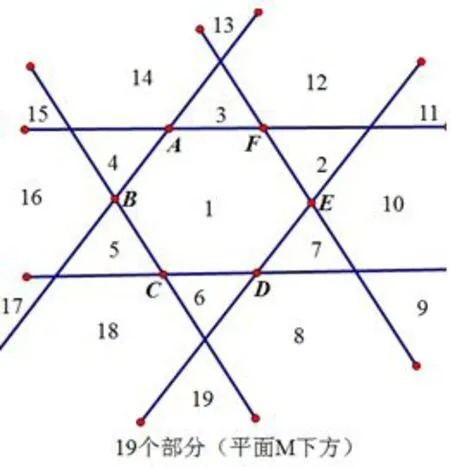
圖7

如圖6,圖7共有8+19=27個(gè)部分.類比四棱臺(tái),可以得到正六棱臺(tái)各個(gè)棱延伸可以把空間分成8+19+19=46個(gè)部分.

2.5 獲得方法

通過限定向上延伸是側(cè)棱延伸,可以得到正偶棱臺(tái)各面延伸問題和正偶棱錐問題相關(guān),正偶棱錐各面延伸問題和正棱柱有直接的聯(lián)系.故可以正棱柱為模型,進(jìn)行研究.

3.形成思路,解答推廣

3.1 正四棱錐各個(gè)面延伸可以把空間分成多少個(gè)部分?

解

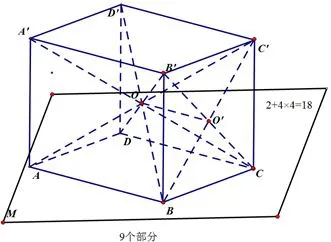
圖8

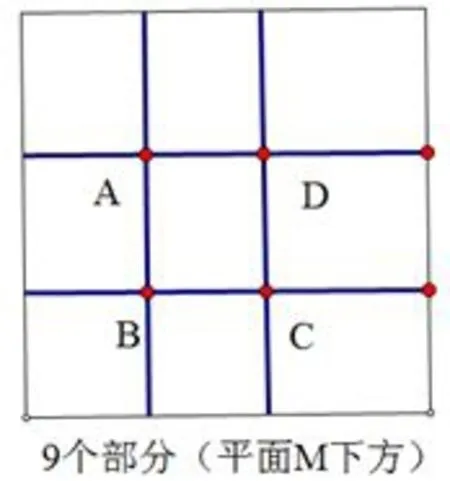
圖9

如圖8,可以將四棱錐O?ABCD側(cè)面向上延伸得到長方體ABCD?A′B′C′D′.于是,平面M上方有O?ABCD,O?ABB′A′,O?BCC′B′,O?CDD′C′,O?DAA′D′,O?A′B′C′D′共6個(gè)部分,其中4個(gè)側(cè)面中的每一個(gè)又被分成了4個(gè)部分,故平面M上方有2+4×4=18個(gè)部分.如圖9,平面M下方有9個(gè)部分,故一共有18+9=27個(gè).

3.2 正四棱臺(tái)各棱可以把空間分成多少個(gè)部分?

解類比2.2,易得答案為27+9=36個(gè).

3.3 正六棱錐各面延伸可以把空間分成多少個(gè)部分?

解

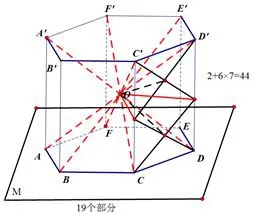
圖10

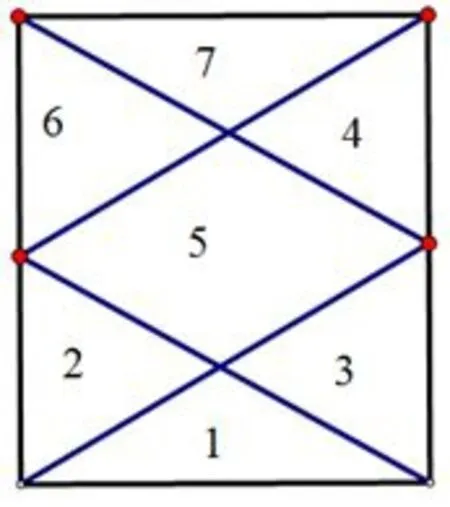
圖11

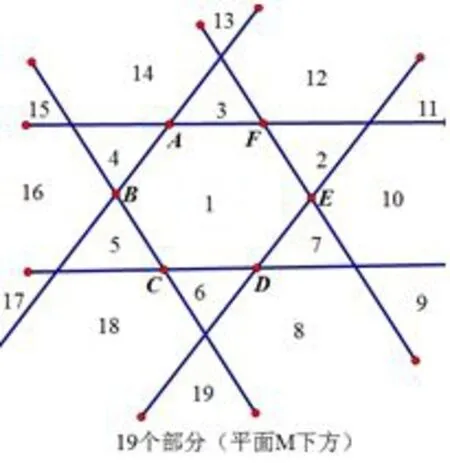
圖12

如圖10,圖11,可以將正六棱錐側(cè)面向上延伸得到直六棱柱,于是,平面M上面有共8個(gè)部分,其中6個(gè)側(cè)面中的每一個(gè)又被分成了7個(gè)部分,故平面M上面有2+6×7=44個(gè)部分.由圖12知平面M下面有19個(gè)部分,故一共有44+19=63個(gè)部分.

類比3.2易得:正六棱臺(tái)將空間分成63+19=82個(gè)部分

3.4 正八棱錐各面延伸可以把空間分成多少個(gè)部分?

解

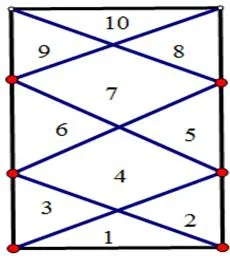
圖13

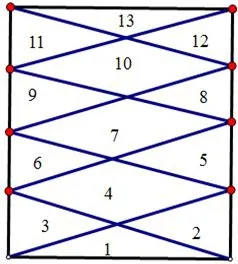
圖14

類比3.3,如圖13可以將正八棱錐側(cè)面向上延伸得到直八棱柱,于是,平面M上方有共10個(gè)部分,其中8個(gè)側(cè)面每個(gè)又被分成了10個(gè)部分,故平面M上方有2+8×10=82個(gè)部分.易得知平面M下方有33個(gè)部分,故一共有82+33=115個(gè)部分.類似的,可以得到正十棱錐每一個(gè)側(cè)面被分成的部分?jǐn)?shù)是13個(gè),如圖14.

3.5 推廣

可以推廣得到如下兩個(gè)定理:

定理1正n棱錐(n為偶數(shù))各個(gè)面延伸可以把空間分成2n2?2n+3個(gè)部分.

解釋由上述例題可知:正n邊形各條邊延長分平面的部分?jǐn)?shù)+2+各側(cè)面被分成的部分?jǐn)?shù)之和.可以驗(yàn)證并遞推的到:正n邊形(n為偶數(shù))各條邊延長分平面的部分?jǐn)?shù)為:.正偶棱錐每個(gè)側(cè)面被分成的部分為:.故答案為:.

定理2正n棱臺(tái)(n為偶數(shù))各個(gè)面延伸可以把空間分成個(gè)部分.

解釋由上述例題可知答案為

正n邊形各條邊延長分平面的部分?jǐn)?shù)×2+2+各側(cè)面被分成的部分?jǐn)?shù)之和.故答案為:

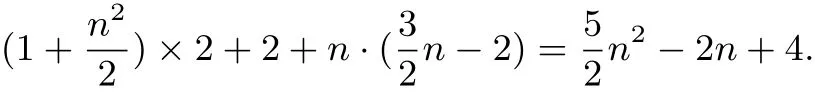
4.總結(jié)與期望

由于筆者水平所限,本文只對(duì)正偶數(shù)的棱錐與棱臺(tái)作出了解答,對(duì)于正奇數(shù)的棱錐與棱臺(tái)的問題,還望各位同仁及專家給出解答與探究.通過大家的共同努力,相信此類問題在不久的將來定會(huì)百花齊放,百家爭鳴!