李國安, 李穆真

(1.寧波大學(xué)金融工程系,浙江 寧波 315211;2.密蘇里大學(xué)統(tǒng)計系,密蘇里 哥侖比亞 65201)

指數(shù)抽樣分布定理及三個期望之極小方差無偏估計的有效性比較

李國安1, 李穆真2

(1.寧波大學(xué)金融工程系,浙江 寧波 315211;2.密蘇里大學(xué)統(tǒng)計系,密蘇里 哥侖比亞 65201)

在相關(guān)文獻(xiàn)工作的基礎(chǔ)上完善指數(shù)抽樣分布定理.首先導(dǎo)出指數(shù)分布樣本最大值與樣本最小值之差的分布,并證明了樣本最大值與樣本最小值之差和樣本最小值相互獨(dú)立;然后導(dǎo)出指數(shù)分布樣本最大值與樣本均值之差的分布,并證明了樣本最大值與樣本均值之差和樣本最小值相互獨(dú)立.從而構(gòu)造出三個期望之極小方差無偏估計,基于樣本均值與樣本最小值之差和樣本最小值構(gòu)造出的期望之極小方差無偏估計,恰好是期望之一致最小方差無偏估計;文末,在小樣本情景下,對上述三個期望之極小方差無偏估計作了有效性比較.

指數(shù)抽樣分布定理;樣本最大值;差;分布;期望;極小方差無偏估計;有效性

1 引言

指數(shù)分布樣本最小值與樣本最大值和樣本均值均是重要的統(tǒng)計量.其中樣本最小值服從指數(shù)分布,樣本均值服從自由度為2n的卡方分布或伽馬分布,樣本均值與樣本最小值之差服從自由度為2(n?1)的卡方分布或伽馬分布,樣本均值與樣本最小值之差與樣本最小值相互獨(dú)立,這些都是熟知的結(jié)果,可參見文獻(xiàn)[1-2].本文繼續(xù)有關(guān)文獻(xiàn)的工作,首先導(dǎo)出了指數(shù)分布樣本最大值與樣本最小值之差的分布,證明了樣本最大值與樣本最小值之差和樣本最小值相互獨(dú)立;然后導(dǎo)出了指數(shù)分布樣本最大值與樣本均值之差的分布,證明了樣本最大值與樣本均值之差和樣本最小值相互獨(dú)立;從而完善了指數(shù)抽樣分布定理.并且從樣本均值與樣本最小值之差和樣本最小值可以構(gòu)造出第一個期望之極小方差無偏估計,它恰好是期望之一致最小方差無偏估計;從樣本最大值與樣本最小值之差和樣本最小值可以構(gòu)造出第二個期望之極小方差無偏估計;從樣本最大值與樣本均值之差和樣本最小值可以構(gòu)造出第三個期望之極小方差無偏估計.由此,在小樣本情景下,對上述三個期望之極小方差無偏估計作了有效性比較.

2 指數(shù)抽樣分布定理

指數(shù)分布總體的順序統(tǒng)計量(X(1),···,X(n))的聯(lián)合分布如下:

定義 2.1設(shè)X～E(α),X1,···,Xn是X～E(α)的容量為n的樣本,(X(1),···,X(n))有如下的密度函數(shù):

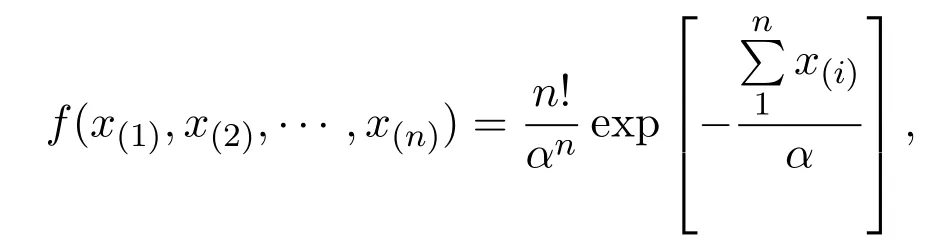
其中x(1)＜x(2)···＜x(n),α＞0,則稱 (X(1),···,X(n))服從多元順序統(tǒng)計量型指數(shù)分布.

記

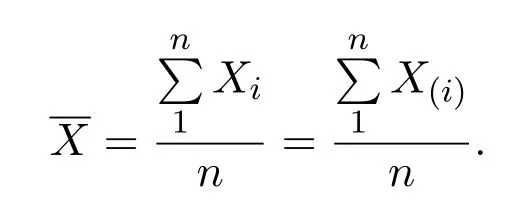
得指數(shù)抽樣分布定理如下:

定理 2.1設(shè)X～E(α),X1,···,Xn是來自X～E(α)的容量為n的樣本,(X(1),···,X(n))為對應(yīng)的順序統(tǒng)計量,則:

證明(1)部分可見文獻(xiàn)[1],因參數(shù)設(shè)置不同及證明的連接性緣故,這里仍然具體寫

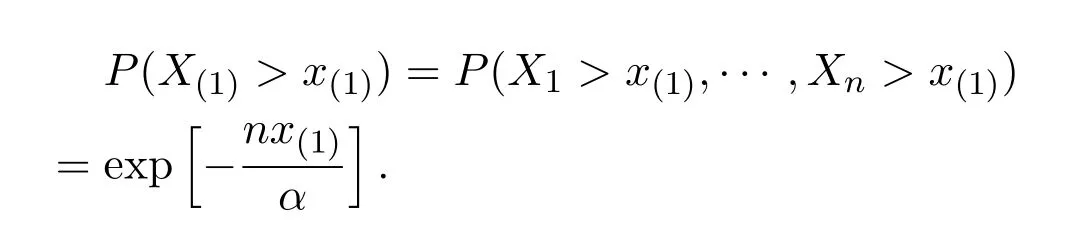
所以,

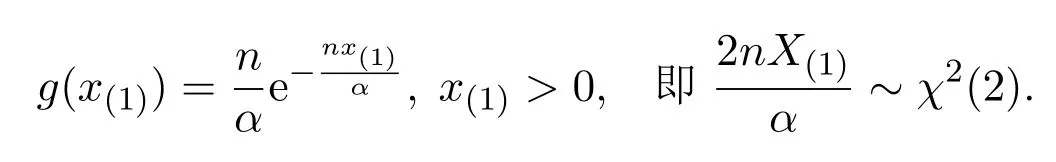
記

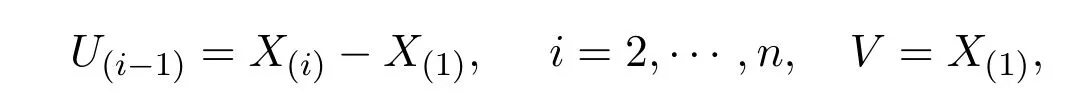
u(i?1)=x(i)?x(1),v=x(1)?x(i)=u(i?1)+v,i=2,···,n.x(1)=v,

則 (U(1),···,U(n?1),V) 的聯(lián)合分布密度為:

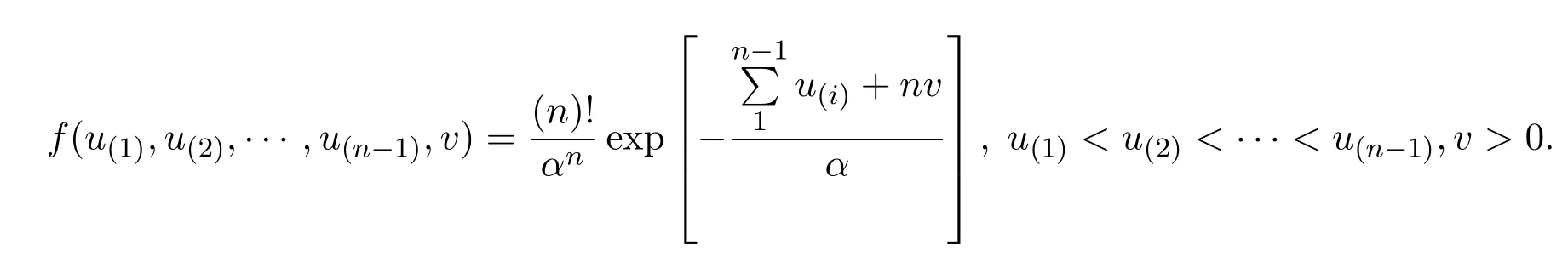
所以,(U(1),···,U(n?1))是來自總體U～E(α)的容量為n?1 的樣本 (U1,···,Un?1)的順序統(tǒng)計量,(U1,···,Un?1)與X(1)相互獨(dú)立.所以,

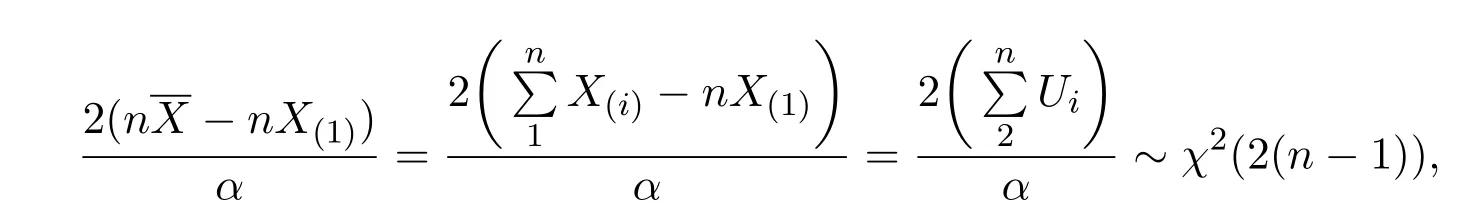
接著證第(2)部分,

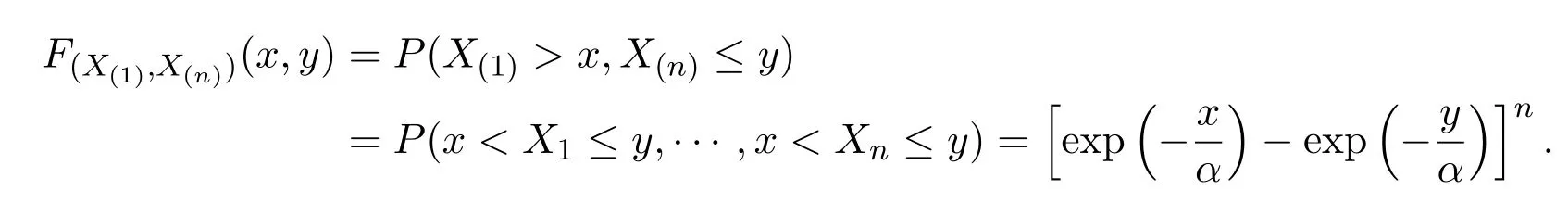
所以,

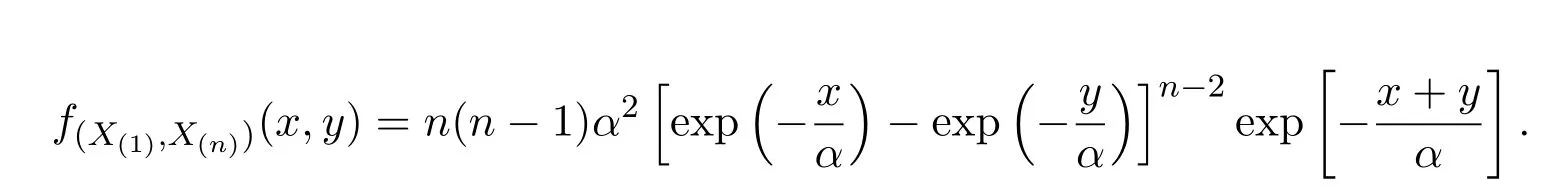
做變換

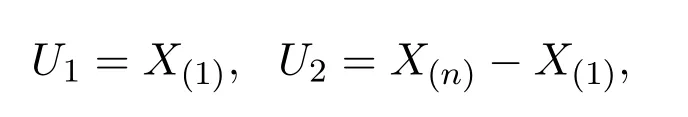
則

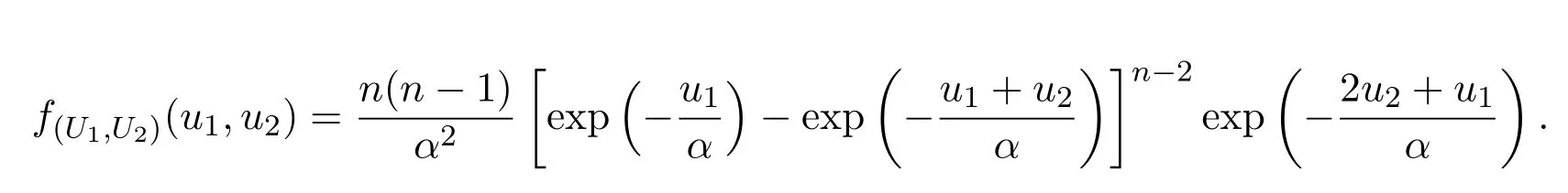
因此,

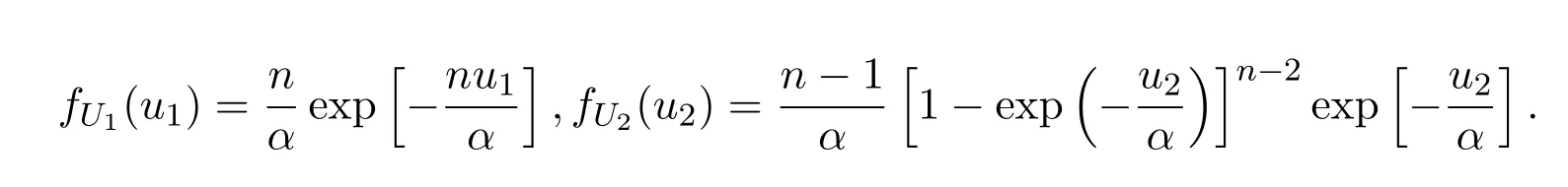
所以,U1與U2相互獨(dú)立,

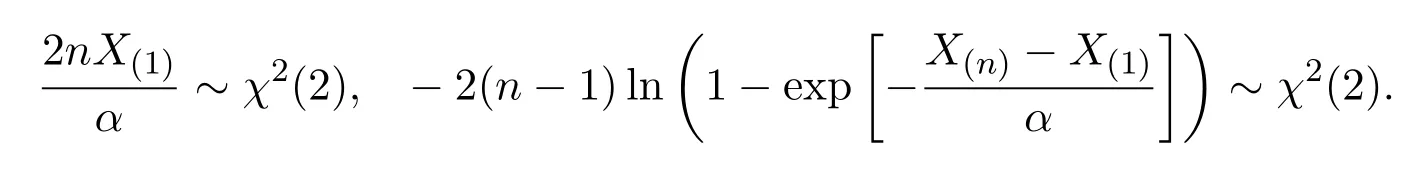
接著證明第 (3) 部分,前記U(i?1)=X(i)?X(1),i=2,···,n,記

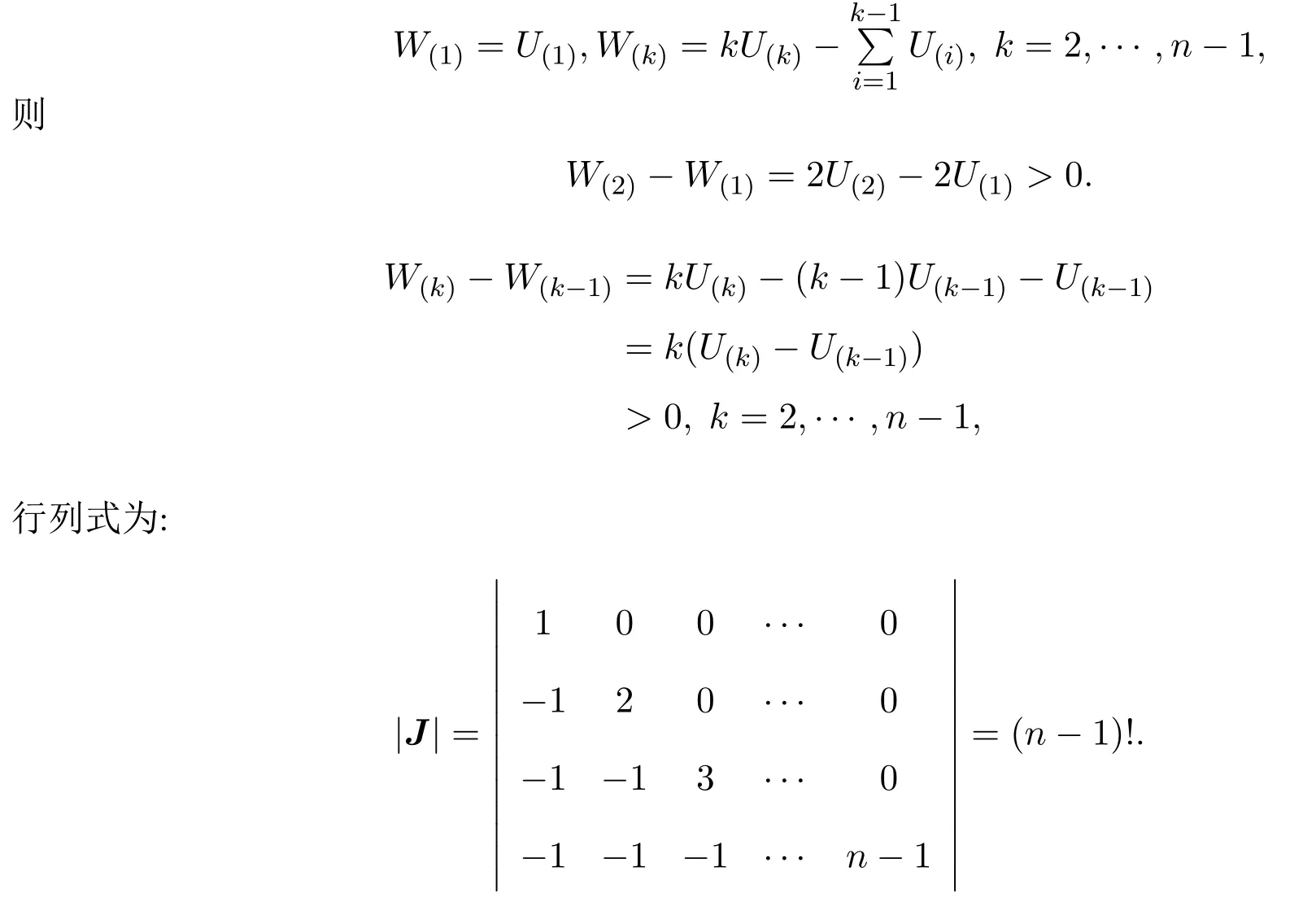
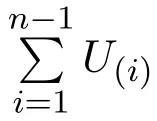
這里列出下面幾種情形:

n=3時,

明顯是一個混合指數(shù)分布的形式.

n=4時,

n=5時,

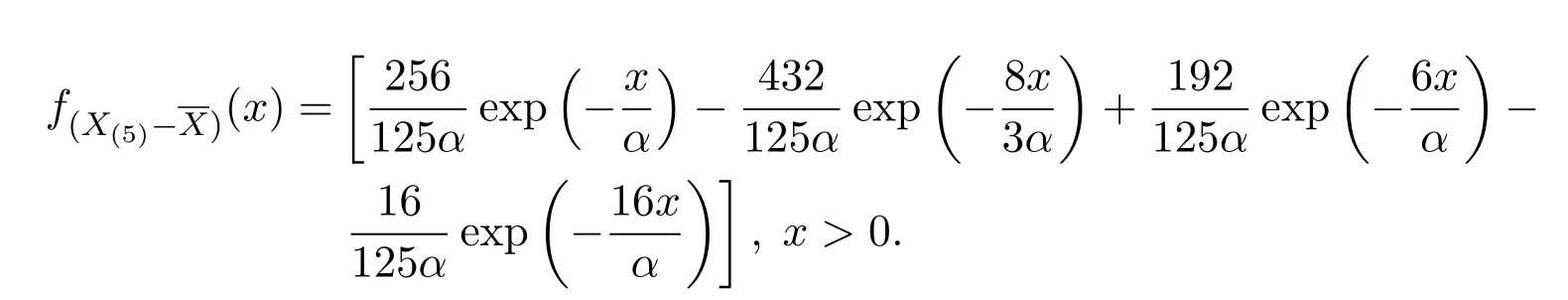
n=6時,

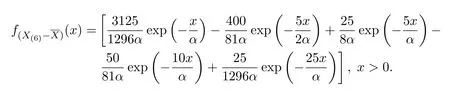
顯然,X(1)與相互獨(dú)立.

3 三個期望之極小方差無偏估計

定理 3.1若X～E(α),X1,···,Xn是來自X～E(α)的容量為n的樣本,(X(1),···,X(n))為對應(yīng)的順序統(tǒng)計量,則基于樣本最小值及樣本均值與樣本最小值之差的期望之極小方差無偏估計恰好為期望之一致最小方差無偏估計.

證明由定理2.1知,

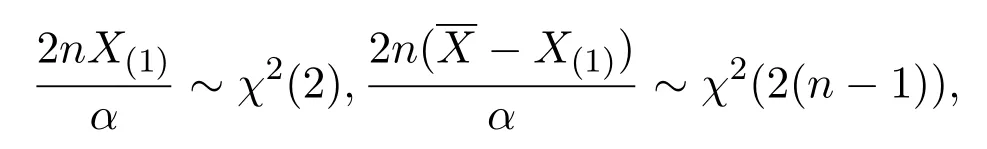
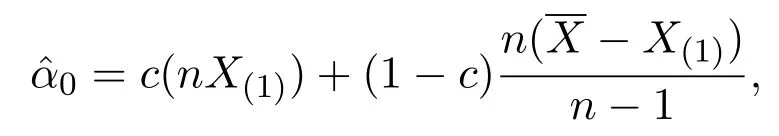
這里

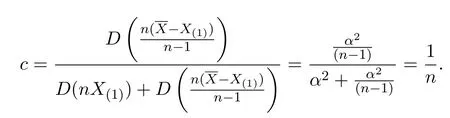
定理 3.2若X～E(α),X1,···,Xn是來自X～E(α)的容量為n的樣本,(X(1),···,X(n))為對應(yīng)的順序統(tǒng)計量,則基于樣本最小值及樣本最大值與樣本最小值之差(X(n)?X(1))的期望之極小方差無偏估計量為,這里

證明

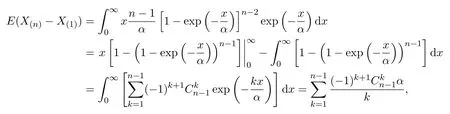
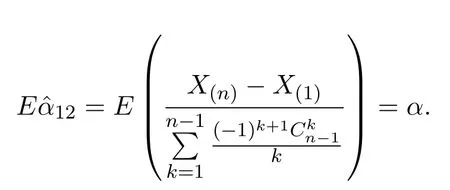
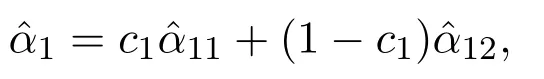
都是α的無偏估計量.

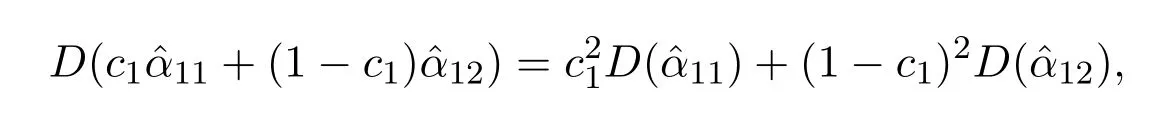
對c1求導(dǎo),并令導(dǎo)數(shù)為零,得

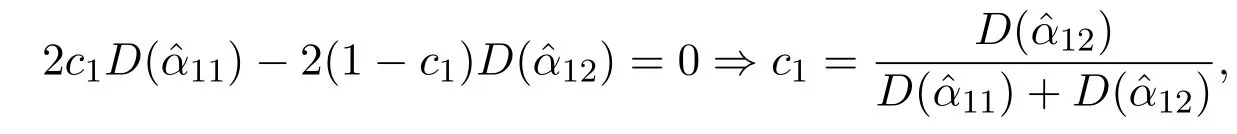
這里

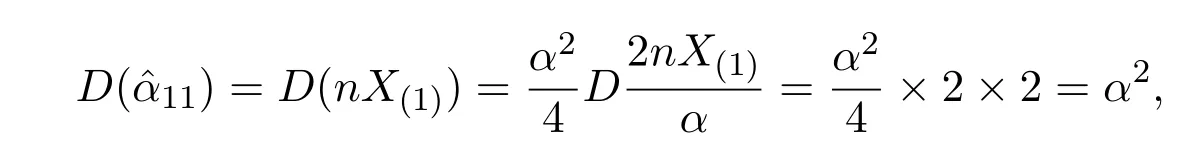
又

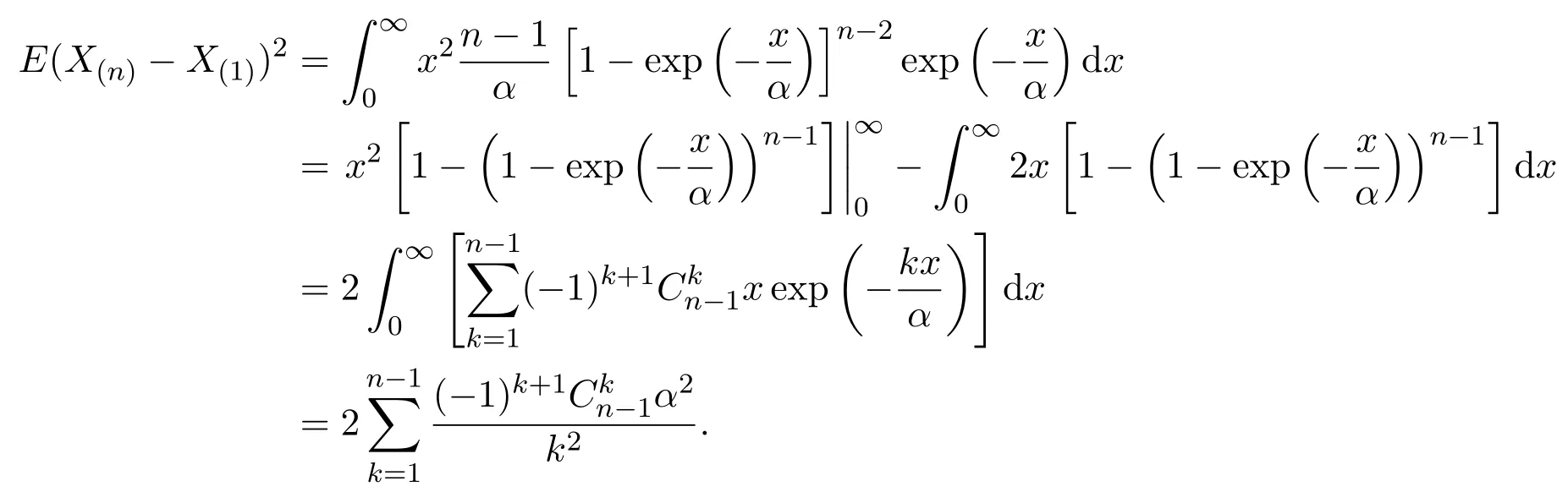
所以,

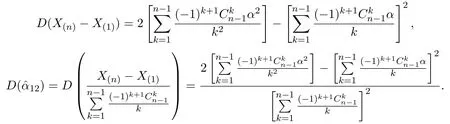
所以,當(dāng)

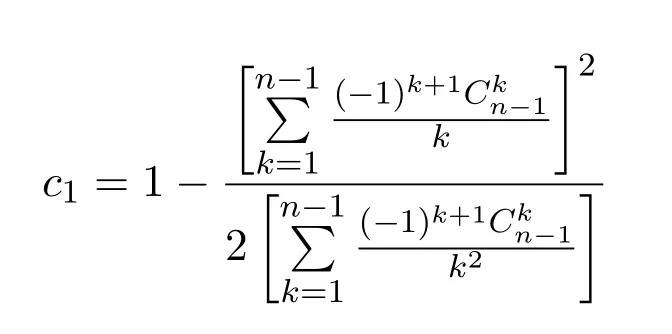
定理 3.3若X～E(α),X1,···,Xn是來自X～E(α)的容量為n的樣本,(X(1),···,X(n))為對應(yīng)的順序統(tǒng)計量,則基于樣本最小值及樣本最大值與樣本均值之差的期望之極小方差的無偏估計量為:

證明,類似于定理3.2,只要算出的期望,二階矩,方差即可.由

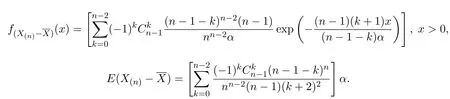
記α前系數(shù)為μ1(n),則

同理寫出

記α2前系數(shù)為μ2(n),則

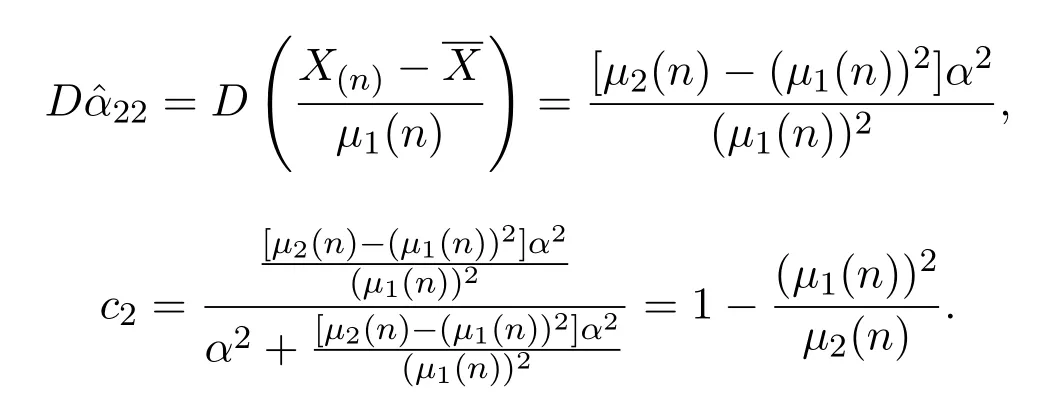
注 3.1三個期望之極小方差無偏估計有效性對比其實(shí)就是三個期望之極小方差無偏估計的方差對比,在此轉(zhuǎn)化為三個期望之無偏估計的方差對比,由

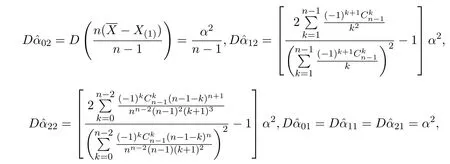
則

取α=1,以下是樣本容量為2至6時三個極小方差無偏估計的方差大小對比(見表1).

表1 小樣本情景下三個極小方差無偏估計的方差大小對比

[1]李國安.指數(shù)分布抽樣基本定理及在四參數(shù)二元Marshall-Olkin型指數(shù)分布參數(shù)估計中的應(yīng)用[J]．統(tǒng)計研究,2016,33(7):98-102．

[2]李國安,李建峰．指數(shù)分布抽樣基本定理及在三參數(shù)一般指數(shù)分布參數(shù)估計中的應(yīng)用[J]．?dāng)?shù)學(xué)的實(shí)踐與認(rèn)識,2017,47(3):165-169．

[3] Lawrance A J,Lewis P A W．Simple dependent pairs of exponential and uniform random variables[J]．Operations Research,1983,31:1179-1197．

[4]Cohen A C,Helm E R．Estimation in the Exponential Distribution[J]．Technometrics,1973,15(2):415-418．

[5]Nie K,Sinha B K,Hedayat A S．Unbiased estimation of reliability function from a mixture of two exponential distributions based on a single observation[J]．Statistics and Probability Letters,2017,127-713．

[6]Al-Saleh M F,Al-Hadhrami S A．Estimation of the mean of the exponential distribution using moving extremes ranked set sampling[J]．Statistical Papers,2003,44:367-382．

[7]Baklizi A,Dayyeh W A．Shrinkage Estimation of P(Y＜X)in the Exponential Case[J]．Communications in Statistics-Simulation and Computation,2003,32(1):31-42．

[8]Dixit U J,Nasiri P N．Estimation of parameters of a right truncated exponential distribution[J]．Statistical Papers,2008,49:225-236．

[9]Gupta R D,Kundu D．Generalized exponential distributions[J]．Australian and New Zealand Journal of Statistics,1999,41:173-188.

[10]Kundu D,Gupta R D．Bivariate generalized exponential distributions[J]．Journal of Multivariate Analysis,2009,100:581-593．

[11]Marshall A W,Olkin I．A multivariate exponential distribution[J]．Journal of American Statistical Association,1967,62(1):30-44．

[12]Arnold B C．Parameter estimation for a multivariate exponential distribution[J]．Journal of American Statistical Association,1968,63:848-852．

Exponential sample theorem and efficiency comparison of three local minimum variance unbiased estimators of mean of the exponential distribution

Li Guoan1,Li Muzhen2

(1.Department of Financial Engineering,Ningbo University,Ningbo 315211,China;2.Department of Statistics,University of Missouri-Columbia Columbia,Missouri65201,USA)

This article continues the works of references,so as to improve and perfect the exponential sample theorem. fi rst,the distribution of the difference between sample maximum and minimum of exponential distribution is derived,and that the difference of these two statistics is mutually independent with the sample minimum is proven.Also,this article derives the distribution of the difference between sample maximum and sample mean,and demonstrates that the difference of these two statistics is mutually independent with the sample minimum.Thus,the three local minimum variance unbiased estimators could be built,the one which is built by sample minimum and the difference between sample mean and sample minimum,is precisely the UMVUE of of mean of the Exponential distribution.At last,in small sample,the efficiency comparison is made among above-mentioned three local minimum variance unbiased estimators of mean of the Exponential distribution.

exponential sample theorem,sample maximum,difference,distribution,mean,local minimum variance unbiased estimator,efficiency

2010 MSC:62D05,62E15,62F10

O212;C811

A

1008-5513(2017)06-0568-10

10.3969/j.issn.1008-5513.2017.06.003

2017-09-04.

寧波大學(xué)學(xué)科項(xiàng)目(XKL14D2037).

李國安(1964-),副教授,研究方向:數(shù)理統(tǒng)計和土地估價.