LIU Wei,LI Bi-wen,LI Zhen-wei,WANG Gan

(School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China)

STABILITY AND HOPF BIFURCATION OF A PREDATOR-PREY BIOLOGICAL ECONOMIC SYSTEM

LIU Wei,LI Bi-wen,LI Zhen-wei,WANG Gan

(School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China)

In this paper,we mainly study the Hopf-bifurcation and the stability of differentialalgebraic biological economic system with predator harvesting.By using the method of stability thoery and Hopf bifurcation theorem dynamical systems and differential algebraic system,we find some related conclusions about stability and Hopf-bifurcation.We have improved the ratio-dependent predator-prey system,take economic effectμas the bifurcation parameter and make a numerical simulation by using Matlab at last,so the conclusions are made more practical.

stability;economic system;Hopf bifurcation;harvesting

2010 MR Subject Classification:34D20;34K18

Document code:AArticle ID:0255-7797(2016)06-1160-13

1　Introduction

According to the lack of biological resources on the earth,more and more people increasingly realized the importance of the modelling and research of biological system.The predator-prey was one of the most popular models that many researchers[1-8]studied and acquired some valuable characters of dynamic behavior.For example,the stability of equilibrium,Hopf bifurcation,flip bifurcation,limit cycle and other relevant conducts.At the same time,the development and utilization of biological resources and artificial arrest was researched commonly in the fields of fishery,wildlife and forestry management by some experts[9-11].Most of them choose differential equations and difference equations to research biological models.It is well known that economic profit become more and more important and take a fundamental gradually situation in social development.In recent years,biological economic systems were researched by many authors[12-16],who describe the system by differential-algebraic equations or differential-difference-algebraic equations.

Basic analysis model which applied by differential-algebraic equations and differentialdifference-algebraic equations are familiar at present.However,there still exist some disadvantages in many systems such as harvesting function.In this paper,the main research isthe stability and Hopf bifurcation of a biological-algebraic biological economic system,which is changed in some details and meaningful.

Our basic model is based on the following ratio-dependent predator-prey system with harvest

where u and v represent the predator density and prey density at time t,respectively,∈,θ and α are all positive constants,and r1and r2stand for the densities of predator and prey populations,and E represents harvesting effort.αEv denotes that the harvests for predator population are proportional to their densities at time t.

In 1954,Gordon[17]studied the effect of the harvest effort on ecosystem form an economic perspective and proposed the following economic principle:

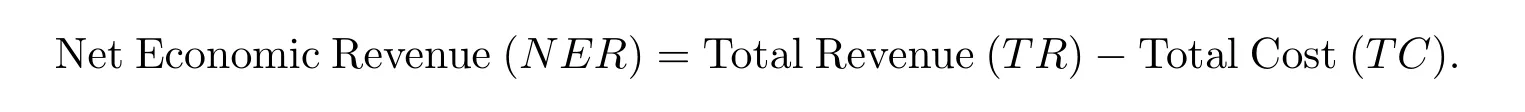
Associated with system(1.1),an algebraic equation which considers the economic profit m of the harvest effort on predator can be established as follows

where E(t)represents the harvest effort,p denotes harvesting reward per unit harvesting effort for unit weight,c represents harvesting cost per unit harvesting effort.Combining the economic theory of fishery resources,we can establish a differential algebraic biological economic system

Nevertheless,the capture effect to predator is not always shown in the liner in nature based on many factors that can affect the predation such as the ability of search,illness and death.Therefore,the harvesting function of system(1.2)is modified as follows

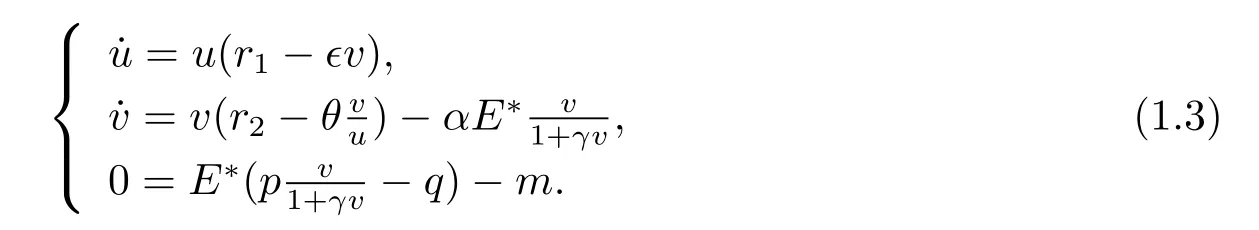
To simplify system(1.2),we use these dimensionless variables

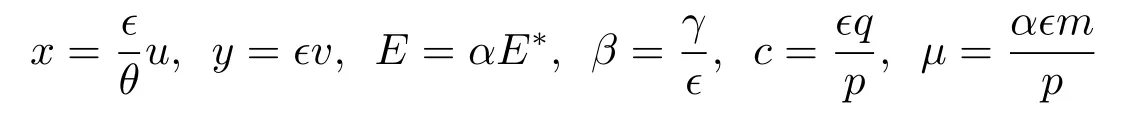
and then obtain the following system

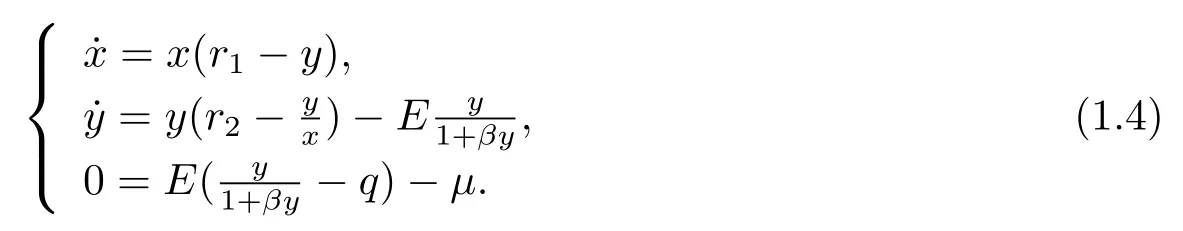
For simplicity,let

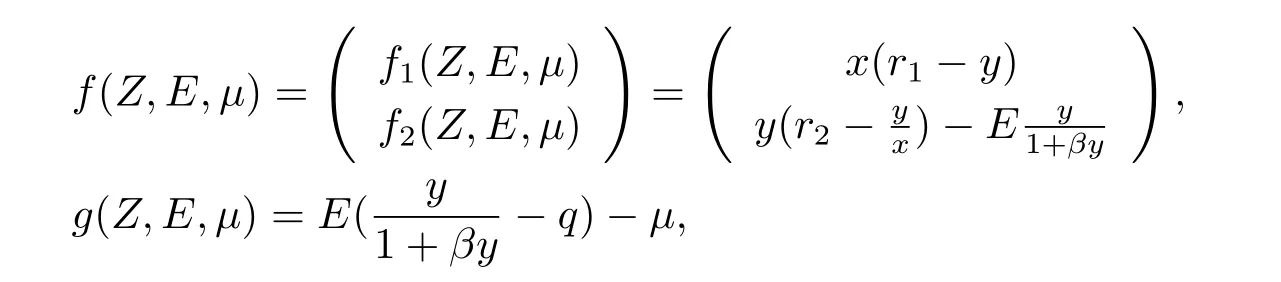
where Z=(x,y)T,μis a bifurcation parameter,which will be defined in the follows.

In this paper,we discuss the effects of the economic profit on the dynamics of system (1.4)in the region={(x,y,E)|x＞0,y＞0,E＞0}.

Next,the paper will be organized as follows.In Section 2,the stability of the positive equilibrium point is discussed by corresponding characteristic equation of system(2.2).In Section 3,we provide Hopf bifurcation analysis of system(1.4).In Section 4,we use numerical simulations to illustrate the effectiveness of result.Then give a brief conclusion in Section 5.

2　Local Stability Analysis of System(1.4)

It is obvious that there exists an equilibrium inif only if this point χ0:=(x0,y0,E0)Tis a real solution of the equations

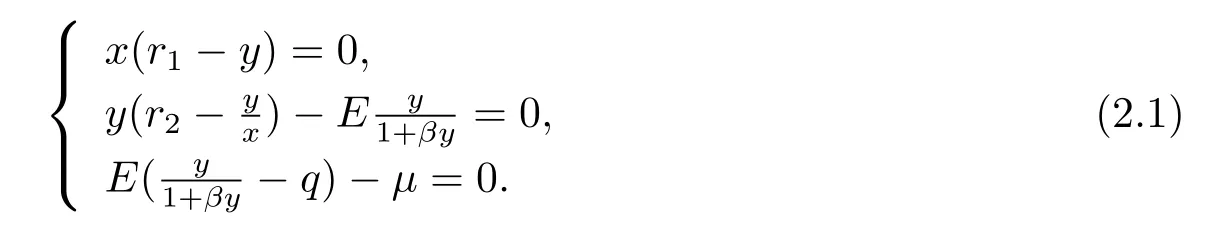
By the calculation,we get

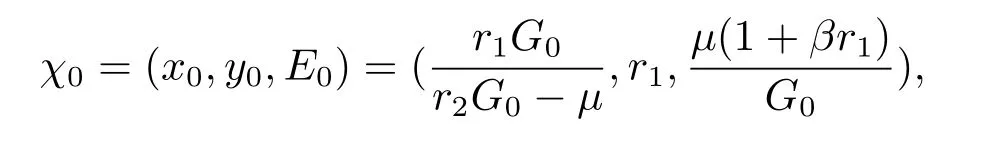
where

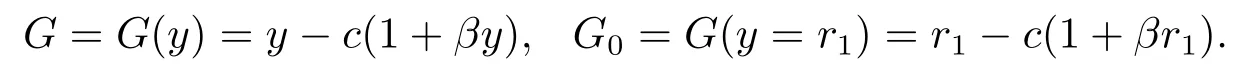
According to this analysis procedure,this essay only concentrate on the interior equilibrium of system(1.4).Based on the ecology meaningful of the interior equilibrium,the predator and the harvest effort to predator are all exist that it is the key point to the study. Thus,a simple assumption that the inequality 0＜μ＜r2G0holds in this paper.Following, we use the linear transformation χT=QMT,where

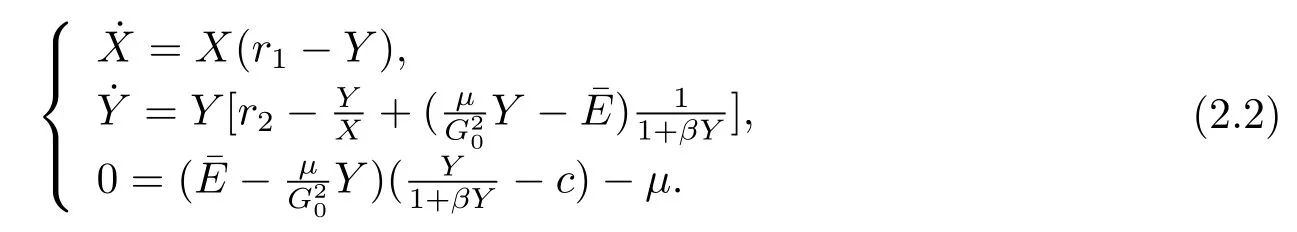
From Section 1,we obtain

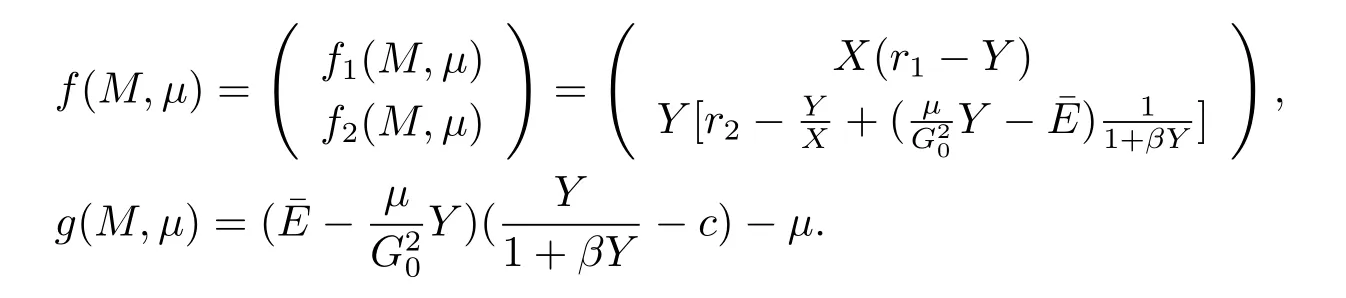
For system(2.2),we consider the local parametric ψ,which defined as follows

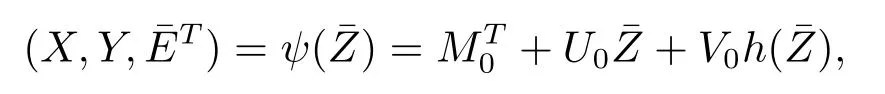
where

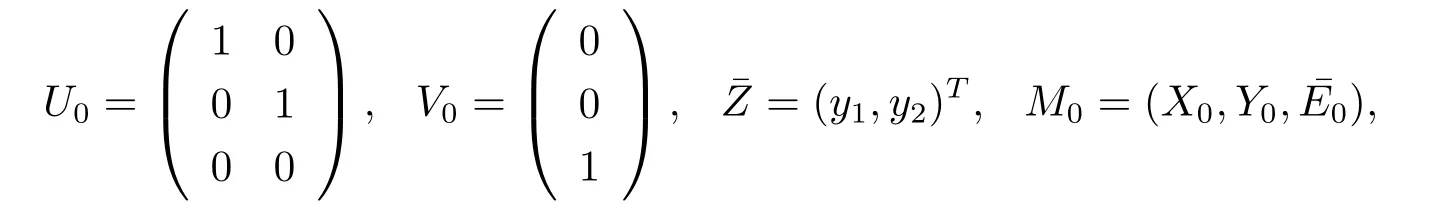
h:R2→R3is a smooth mapping.Then we can obtain the parametric system(2.2)as follows:

More details about the definition can be found in[18].Based on system(2.3),we can get Jacobian matrix E(M0),which takes the form of

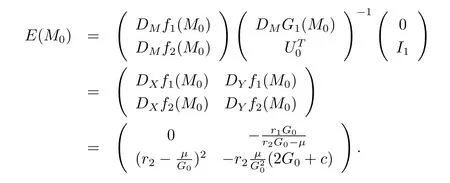
Then the following theorem summarizes the stability of the positive equilibrium point of system(1.4).

Theorem 2.1 For system(2.2)

(ii)If(r2-μ)2＜4r1andμ＜minthe positive equilibrium point of system(1.4)is a sink;otherwise when＜μ＜r2G0,the positive equilibrium point of system(1.4)is a source.

Proof First,the characteristic equation of the matrix E(M0)can be written as

Now donate?by

Remark 1 The local stability of χ0is equivalent to the local stability of M0.

Remark 2 When the roots of eq.(2.4)exist zero real parts,system(1.4)will occur bifurcation,which will be discussed in Section 3.

3　Hopf Bifurcation Analysis of the Positive Equilibrium

In this section,we discuss the Hopf bifurcation from the equilibrium point χ0by choosing μas the bifurcation parameter.Based on the Hopf bifurcation theorem in[19],we need find some sufficient conditions.

According to the definition of?,we obtain

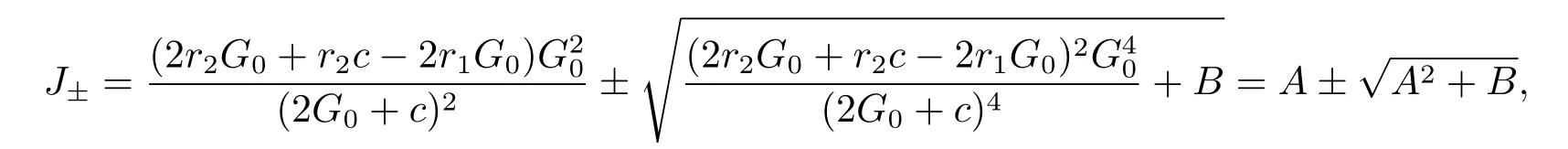
where

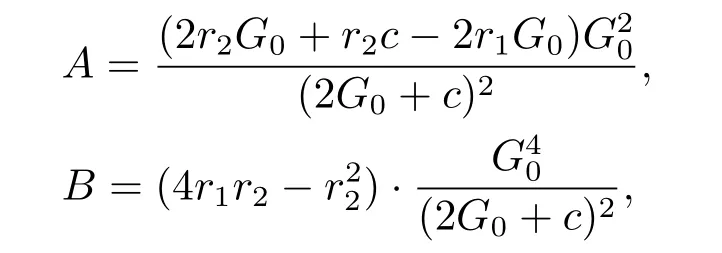
here,we assume that A2+B≥0 in this paper.

Thus,for eq.(2.4),if B＞0 and 0＜μ＜min{r2G0,J+}.Eq.(2.4)has one pair of imaginary roots.When B＞0,A＞0,J-＜r2G0and J-＜μ＜min{r2G0,J+},eq.(2.4) has one pair of imaginary roots.

In the case of meet the above conditions,we can get the roots as follows:

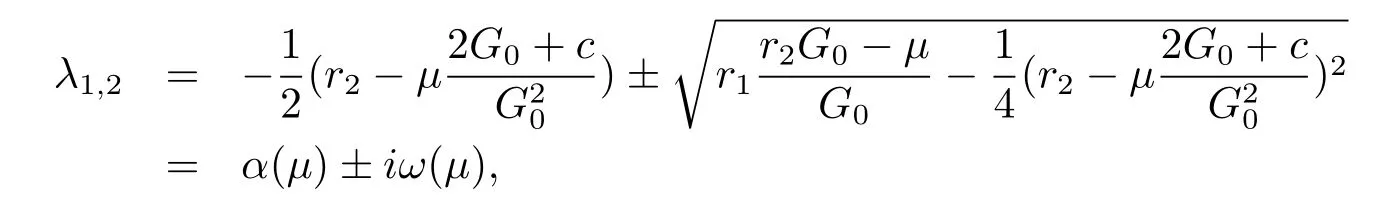
where

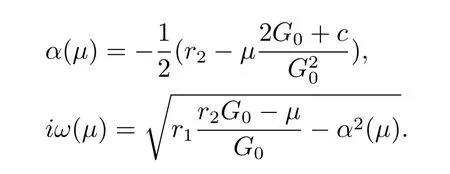
By calculating,we obtain

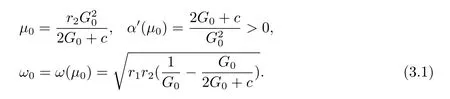
Eq.(3.1)indicates that eq.(2.2)occurs Hopf bifurcation atμ0.

In order to calculate the Hopf bifurcation,we need to lead the normal form of system (2.2)as follows

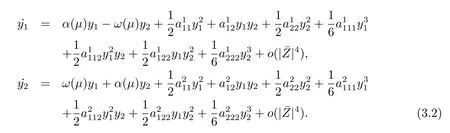
From eq.(2.3),we have

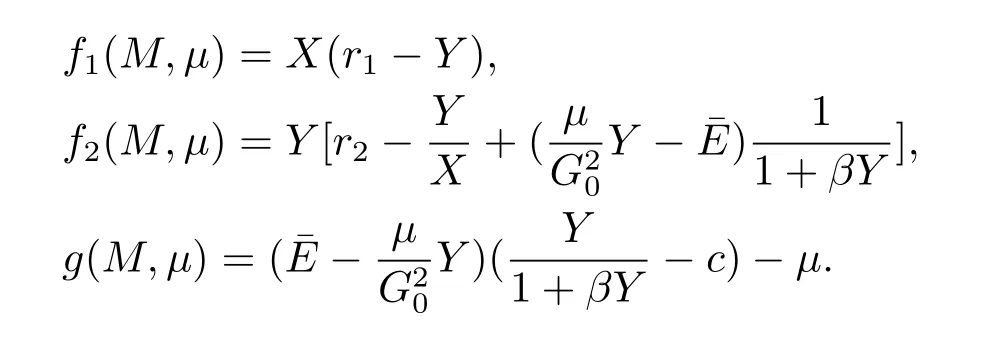
Then we can easily obtain

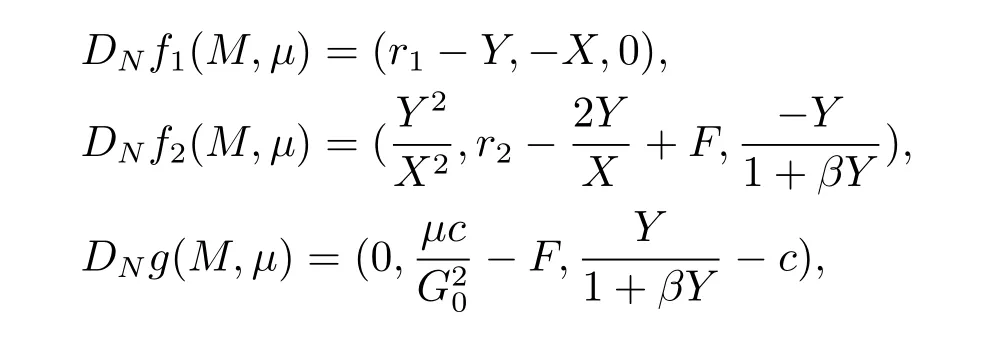
where

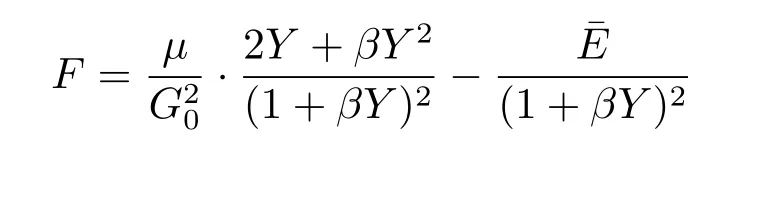
and

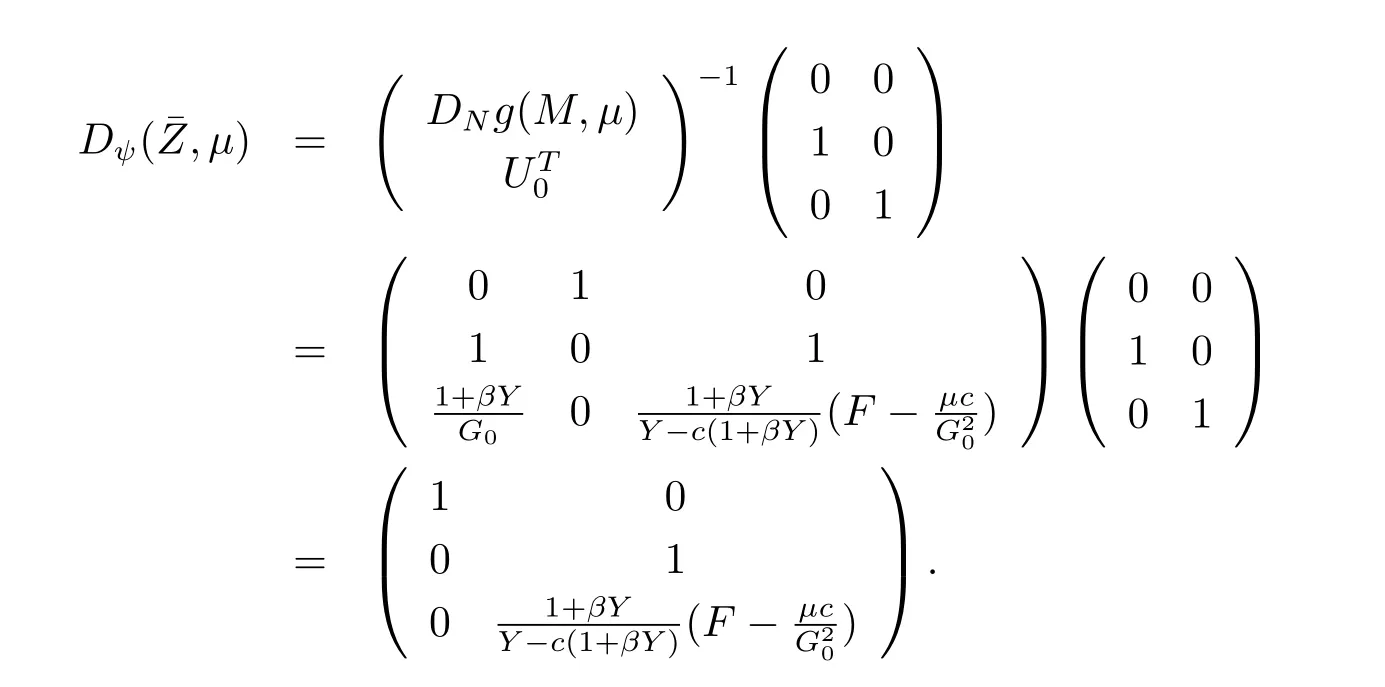
Then we get

Thus we have

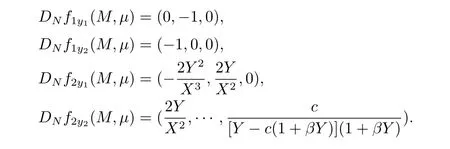
Then we obtain

Substituting M0,μ0into above,we have

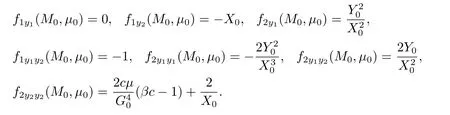
Now,we get

Finally,we obtain

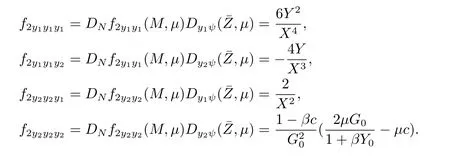
Thus we have eq.(3.3)

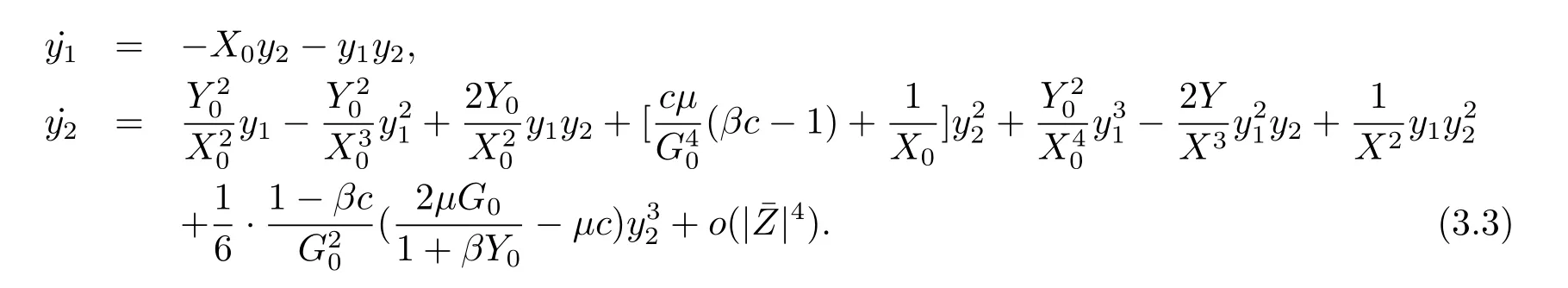
Comparing with the normal form(3.2),we chosse the nonsingular matrix

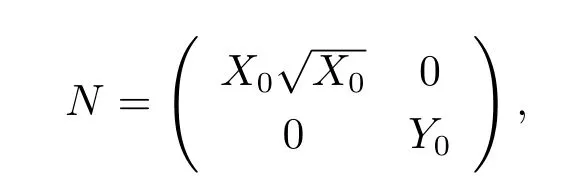
then we use the linear transformation H=N,noticing ω0=,we derive the normal form as follows

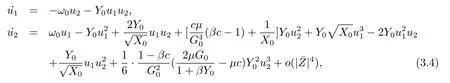
where H=(u1,u2)T.Then

According to the Hopf bifurcation theorem in[19],now we only need to calculate the value of a

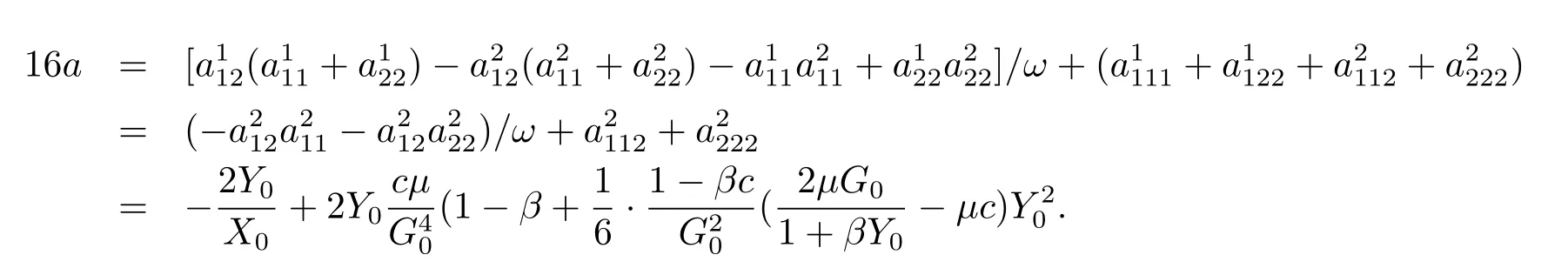
Next,there are two cases should be discussed.That is a＞0 and a＜0.Based on the Hopf bifurcation theorem in[19],we obtain Theorem 3.1.

Theorem 3.1 For the system(2.2),there exist an ε＞0 and two small enough neighborhoods P1and P2of χ0(μ),where P1?P2.

(i)If

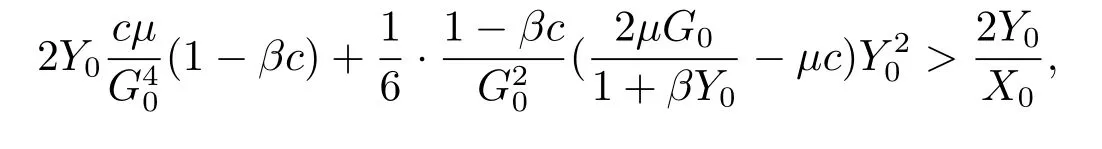
then

(1)whenμ0＜μ＜μ0+ε,χ0(μ)is unstable,and repels all the points in P2;

(2)whenμ0-ε＜μ＜μ0,there exist at least one periodic solution in1,which is the closure of P1,one of them repel all the points in1{χ0(μ)},and also have another periodic solution(may be the same that)repels all the points in P21,and χ0(μ)is locally asymptotically stable.

(ii)If

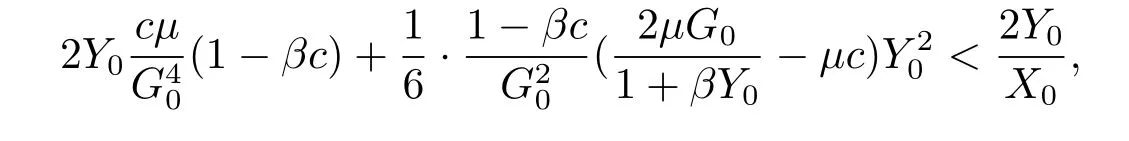
then

(1)whenμ0-ε＜μ＜μ0,χ0(μ)is locally asymptotically stable,and repels all the points in P2;

(2)whenμ0＜μ＜μ0+ε,there exist at least one periodic solution in1,one of them repel all the points in1{χ0(μ)},and also have another periodic solution(may be the same that)repels all the points in P21,and χ0(μ)is unstable.

Proof Theorem 3.1 can be similarly proved as the Hopf bifurcation theorem in[19],so we omit the process here.

4　Numerical Simulations

In this section,we give a numerical example of system(1.4)with the parameters r1= 3,r2=1,c=1,β=0.195,then system(1.4)becomes

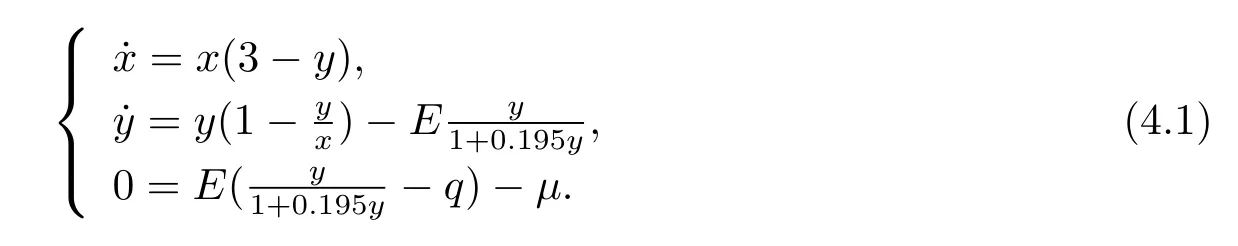
By simple computing,the only positive equilibrium point of above system is

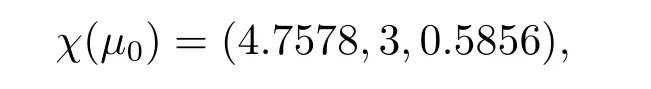
and the Hopf bifurcation valueμ0=

Therefore,by Theorem 3.1,we can easily show that the positive equilibrium point χ0(μ) of system(4.1)is locally asymptitically stable whenμ=0.505＜μ0as is illustrated by computer simulations in Fig.1;periodic solutions occur from χ0(μ)whenμ=0.5195＜μ0as is illustrated in Fig.2;the positive equilibrium point χ0(μ)of system(4.1)is unstable whenμ=0.535＞μ0as is illustrated in Fig.3.

Figure 1:Whenμ=0.505＜μ0,that show the positive equilibrium point χ0(μ)is locally asymptotically stable.

Figure 2:Periodic solutions bifurcating from χ0(μ)whenμ=0.5195＜μ0.

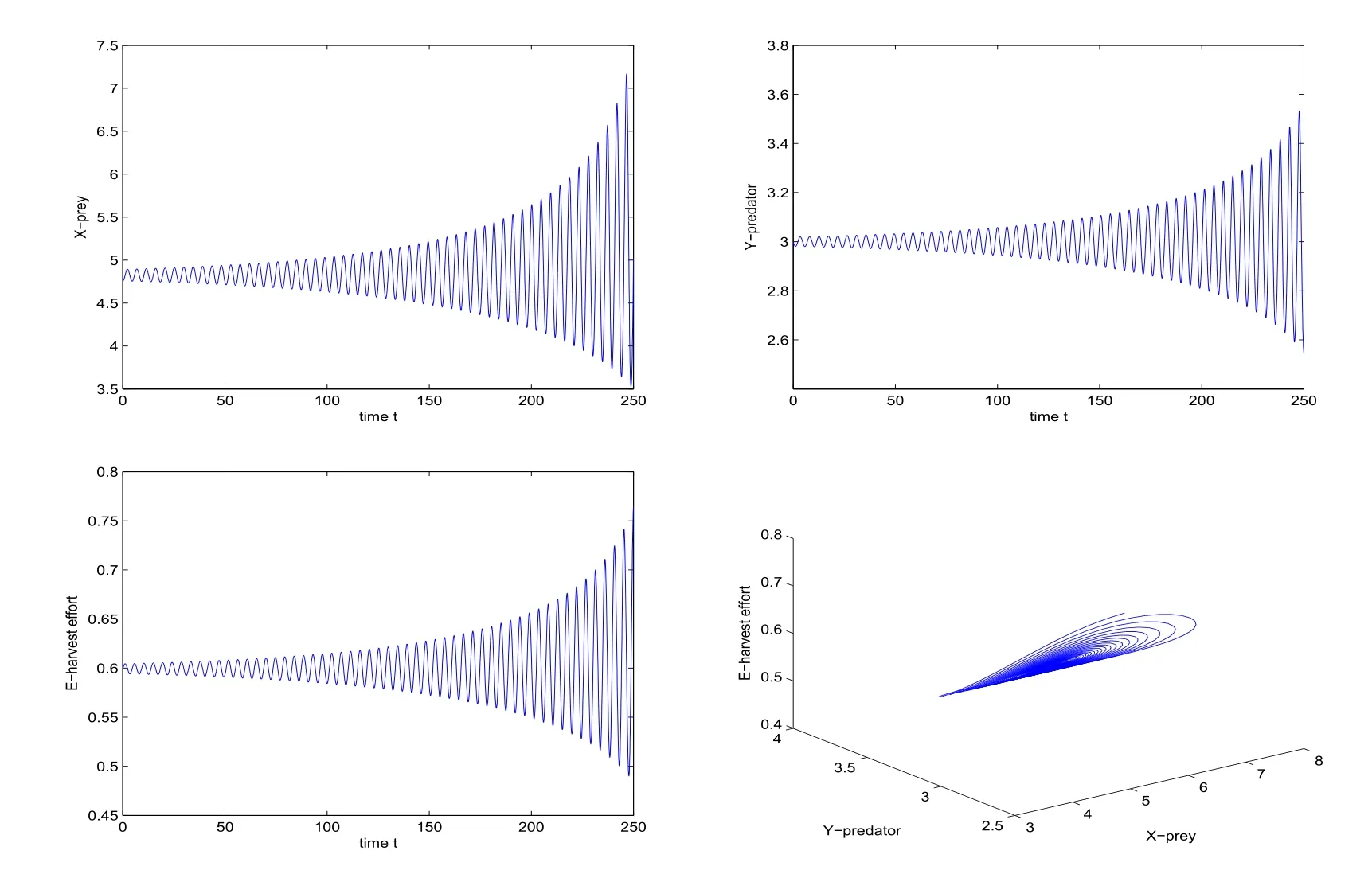
Figure 3:Whenμ=0.535＞μ0,that show the positive equilibrium point χ0(μ)is unstable.

5　Conclusions

Based on the above inference and calculation,we find that economic effect will influence the stability of differential-algebraic biological economic system.For instance,according to those statistics and graphs,if people fix the economic index at a high level,over the bifurcation value of Hopf-bifurcation,the system will become unstable that means people have destroyed the economic balance even led to the extinction of ecologic species.Therefore, with an aim to realize the harmonious sustainable development co-existence between man and nature,we should not seek economic effect blindly and control it within a certain limit, such as less than bifurcation value.

In addition,we can make some improvements in our model.For example,we do not consider the influence of time delays and double harvesting that is,human harvesting will harvest predator and prey at the same time.So it is necessary for us to go on with our research in these aspects in the future.

References

[1]Chen B S,Liu Y Q.On the stable periodic solutions of single sepias models with hereditary effects[J]. Math.Appl.,1999,12:42-46.

[2]Xiao D M,Li W X,Han M A.Dynamics in ratio-dependent predator-prey model with predator harvesting[J].J.Math.Anal.Appl.,2006,324(1):14-29.

[3]Zhang Y,Zhang Q L.Chaotic control based on descriptor bioeconomic systems[J].Contr.Dec., 2007,22(4):445-452.

[4]Pan K,Li B W.Existence of positive periodic solution for two-patches predator-prey impulsive diffusion delay system with functional response[J].J.Math.,2010,30(1):183-190.

[5]Li P L,Yu C C,Zeng X W.The qualitative analysis of a class of predator-prey system with functional response[J].J.Math.,2006,26(2):217-222.

[6]Qu Y,Wei J J.Bifurcation analysis in a predator-prey system with stage-structure and harvesting[J]. J.Franklin Institute,2010,347:1097-1113.

[7]Rebaza J.Dynamical of prey threshold harvesting and refuge[J].J.Comput.Appl.Math.,2012, 236:1743-1752.

[8]Gupta R P,Chandra P.Bifurcation analysis of modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting[J].J.Math.Anal.Appl.,2013,398:278-295.

[9]Liu C,Zhang Q L,Zhang Y,Duan X D.Bifurcation and control in a differential-algebraic harvested prey-predator model with stage structure for predator[J].Int.J.Bifurcation Chaos,2008,18:3159-3168.

[10]Chen L N,Tada Y,Okamoto H,Tanabe R,Ono A.Optimal operation solutions of power systems with transient stability constraints[J].IEEE Trans.Circuits Syst.,2001,48:327-339.

[11]Liu X X,Li B W,Chen B S.Global stability for a predator-prey model with disease in the prey[J]. J.Math.,2013,33(1):69-73.

[12]Zhang G D,Zhu L L,Chen B S.Hopf bifurcation and stability for a differential-algebraic biological economic system[J].Appl.Math.Comput.,2010,217:330-338.

[13]Chen B S,Chen J J.Bifurcation and chaotic behavior of a discrete singular biological economic system[J].Appl.Math.Comput.,2012,219:2371-2386.

[14]Liu W,Fu C J,Chen B S.Hopf bifurcation for a predator-prey biological economic system with Holling type II functional response[J].J.Franklin Institute,2011,348:1114-1127.

[15]Liu W,Fu C J.Hopf bifurcation of a modified Leslie-Gower predator-prey system[J].Cogn Comput., 2013,5:40-47.

[16]Zhang G D,Zhu L L,Chen B S.Hopf bifurcation in a delayed differential-algebraic biological economic system[J].Nonl.Anal.:Real World Appl.,2011,12:1708-1719.

[17]Gordon H S.Economic theory of a common property resource:the fishery[J].J.Polit.Econ.,1954, 62(2):124-142.

[18]Chen B S,Liao X X,Liu Y Q.Normal forms and bifurcations for the differential-algebraic systems[J]. Acta Math.Appl.Sinica,2000,23(3):429-443(in Chinese).

[19]Gukenheimer J,Holmes P.Nonlinear oscillations,dynamical systems,and bifurcations of vector fields[M].New York:Springer-Verlag,1983.

一類捕食食餌微分經(jīng)濟系統(tǒng)的穩(wěn)定性與Hopf分支

劉煒,李必文,李震威,汪淦

(湖北師范學院數(shù)學與統(tǒng)計學院,湖北黃石435002)

本文主要研究了一個帶有對捕食者進行捕獲的微分代數(shù)經(jīng)濟系統(tǒng)的穩(wěn)定性和Hopf分支問題.利用了動力系統(tǒng)和微分代數(shù)系統(tǒng)中的穩(wěn)定性理論和分支理論的方法,得到了穩(wěn)定性和Hopf分支穩(wěn)定性的相關結(jié)論.本文對Ratio-Dependent捕食食餌模型進行了一定程度的完善,并且選取經(jīng)濟效益μ為分支參數(shù)進行研究,最后利用Matlab進行數(shù)值模擬,這樣使得到的結(jié)論更符合現(xiàn)實意義.

穩(wěn)定性;經(jīng)濟系統(tǒng);Hopf分支;捕獲

MR(2010)主題分類號:34D20;34K18O29;O193

?date:2014-04-03Accepted date:2014-11-11

Supported by the Research Project of Hubei Provincial Department of Education of China under Grant(T201412).

Biography:Liu Wei(1989-),female,born at Taiyuan,Shanxi,master,major in ordinary differential equations and control theory.