COMPLETE MOMENT CONVERGENCE OF WEIGHTED SUMS FOR ARRAYS OF DEPENDENT RANDOM VARIABLES
GUO Ming-le,DAI Yu,ZHANG Li-jun
(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)
COMPLETE MOMENT CONVERGENCE OF WEIGHTED SUMS FOR ARRAYS OF DEPENDENT RANDOM VARIABLES
GUO Ming-le,DAI Yu,ZHANG Li-jun
(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)
In this paper,the complete moment convergence of weighted sums for sequences of dependent random variables is investigated.By applying moment inequality and truncation methods,some sufficient conditions of complete moment convergence of weighted sums for sequences of dependent random variables are established.We extend the results of Volodin et al.(2004) and Chen et al.(2006)for independent random variables to negatively associated and negatively dependent random variables,which improve and generalize the results of Sung(2011),Wu(2012) and Guo and Zhu(2012).
negatively associated;negatively dependent;ρ?-mixing;complete moment convergence;complete convergence
2010 MR Subject Classification:60F15
Document code:AArticle ID:0255-7797(2016)06-1120-13
1 Introduction
Hsu and Robbins[1]introduced the concept of complete convergence of{Xn}.A sequence{Xn,n=1,2,···}is said to converge completely to a constant C if

Moreover,they proved that the sequence of arithmetic means of independent identically distributed(i.i.d.)random variables converge completely to the expected value if the variance of the summands is finite.The converse theorem was proved by Erds[2].In view of the Borel-Cantelli lemma,the complete convergence implies that almost sure convergence. Therefore the complete convergence is very important tool in establishing almost sure convergence.The result of Hsu-Robbins-Erds is a fundamental theorem in probability theory and was generalized and extended in several directions by many authors.
We recall that the array{Xni,i≥1,n≥1}of random variables is said to be stochastically dominated by a random variable X if there exists a positive constant C,such that P{|Xni|>x}≤CP{|X|>x}for all x≥0,i≥1 and n≥1.
Volodin et al.[3]and Chen et al.[4](β>-1 and β=-1,respectively)obtained complete convergence for weighted sums of arrays of rowwise independent Banach-spacevalued random elements.
Theorem 1.1[3,4]Suppose that β≥-1.Let{Xni,i≥1,n≥1}be an array of rowwise independent random elements in a real separable Banach space which are stochastically dominated by a random variable X.Let{ani,i≥1,n≥1}be an array of constants satisfying

and

for some 0<θ≤2 andμsuch that θ+μ/r<2 and 1+μ+β>0.If E|X|θ+(1+μ+β)/r<∞Xni→0 in probability,then
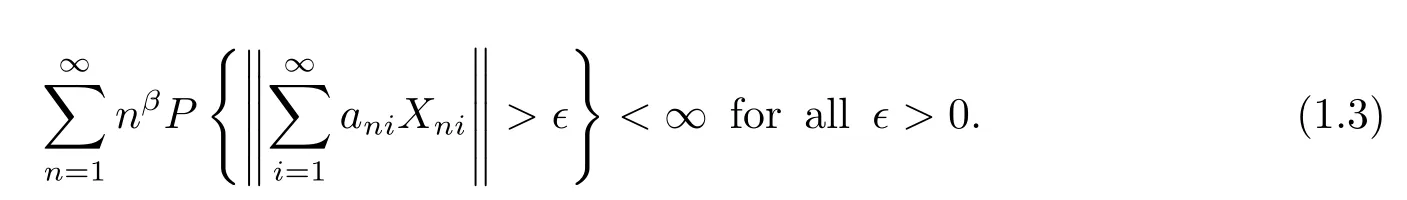
If β<-1,then(1.3)is immediate.Hence Theorem 1.1 is of interest only for β≥-1.
Recently,Sung[5]extended Theorem 1.1 to negatively associated and negatively dependent random variables when θ=1.Moreover,similar results for sequences of φ-mixing and ρ?-mixing random variables are also established.
Theorem 1.2[5]Suppose that β≥-1.Let{Xni,i≥1,n≥1}be an array of rowwise negatively associated random variables which are stochastically dominated by a random variable X.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and
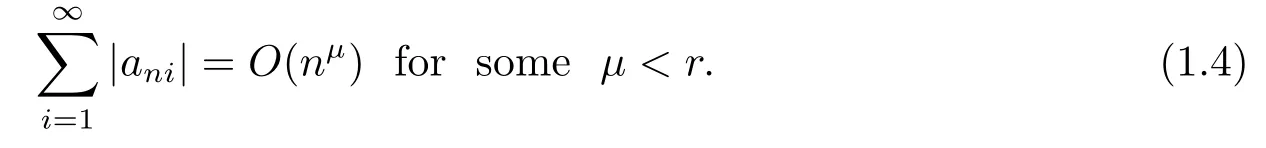
If EXni=0 for all i≥1,n≥1 and

then

Guo and Zhu[6]extended Theorem 1.2 to complete moment convergence of the supremum of partial sums for arrays of negatively associated random variables when β>-1. However,the proof of Guo and Zhu[6]does not work for the case of β=-1.
Theorem 1.3[6]Under the conditions of Theorem 1.2.If β>-1,then
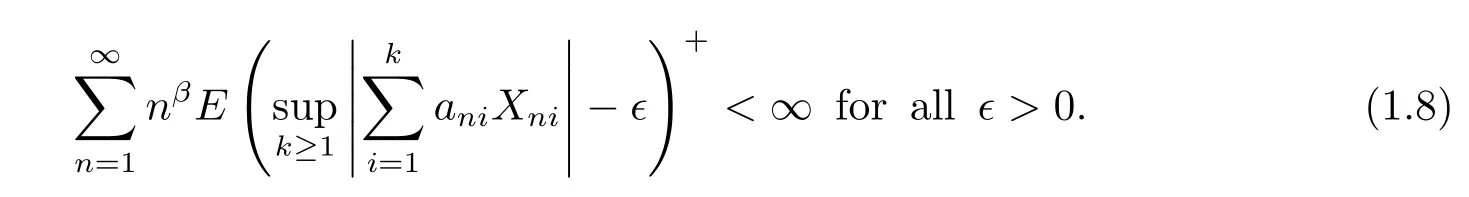
Wu[7]extended Theorem 1.1 to negatively dependent random variables when β>-1. Wu[7]also considered the case of 1+μ+β=0(β>-1).However,the proof of Wu[7]does not work for the case of β=-1.
Theorem 1.4[7]Suppose that β>-1.Let{Xni,i≥1,n≥1}be an array of rowwise negatively dependent random variables which are stochastically dominated by a random variable X.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and(1.2)for some θ andμsuch thatμ<2r and 0<θ<min{2,2-μ/r}.Furthermore,assume that EXni=0 for all i≥1 and n≥1 if θ+(1+μ+β)/r≥1.If
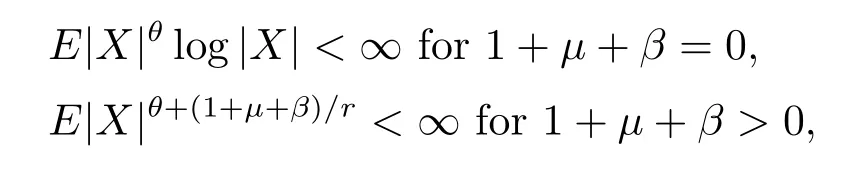
then

In this paper,We deal with more general weights and establish some weaker sufficient conditions for complete moment convergence of weighted sums for arrays of negatively associated and negatively dependent random variables.Similar results for sequences of ρ?-mixing random variables are also obtained.The results of Volodin et al.[3],Chen et al.[4],Sung [5],Wu[7]and Guo and Zhu[6]are improved and generalized.
For the proofs of the main results,we need to restate a few lemmas for easy reference. Throughout this paper,the symbol C denotes a positive constant which is not necessarily the same one in each appearance,I(A)denotes the indicator function of A.For a finite set B,the symbol#B denotes the number of elements in the set B.Let an?bndenote that there exists a constant C>0 such that an≤Cbnfor sufficiently large n.Also,let logx denote lnmax(e,x).
Lemma 1.1[5]Let the sequence{Xn,n≥1}of random variables be stochastically dominated by a random variable X.Then for any p>0,x>0,
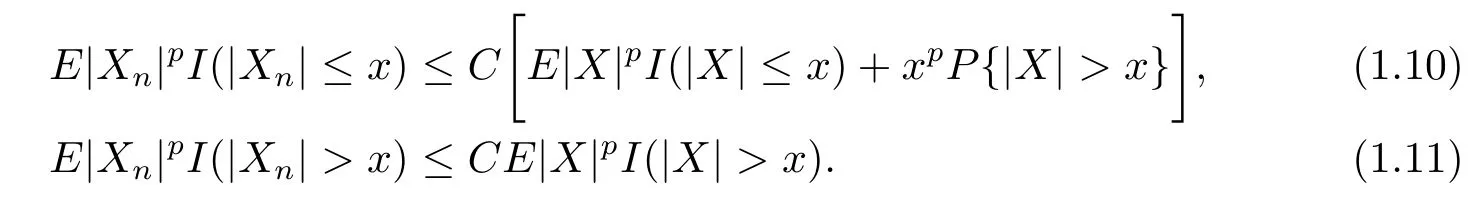
The following lemma is well known,and its proof is standard.
Lemma 1.2 Let X be a random variable.For any α>0,r>0,the following statements hold:
One of the most interesting inequalities to probability theory is the Rosenthal-type inequality.The Rosenthal-type inequality plays an important role in establishing complete convergence.The Rosenthal-type inequalities for sequences of dependent random variables were established by many authors.
The concept of negatively associated random variables was introduced by Alam and Saxena[8]and was carefully studied by Joag-Dev and Proschan[9].A finite family of random variables{Xi,1≤i≤n}is said to be negatively associated,if for every pair disjoint subset A and B of{1,2,···,n}and any real nondecreasing coordinate-wise functions f1on RAand f2on RB,
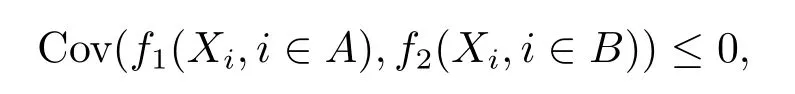
whenever the covariance exists.An infinite family of random variables{Xi,-∞<i<∞} is negatively associated if every finite subfamily is negatively associated.
The following lemma is a Rosenthal-type inequality for negatively associated random variables.
Lemma 1.3[10]Let{Xn,n≥1}be a sequence of negatively associated random variables with EXn=0 and E|Xn|p<∞for any n≥1,p≥1.Then there exist constants Cp>0 and Dp>0 depending only on p such that,

and

The concept of negatively dependent random variables was given by Lehmann[11].A finite family of random variables{Xi,1≤i≤n}is said to be negatively dependent(or negatively orthant dependent)if for all real numbers x1,x2,···,xn,
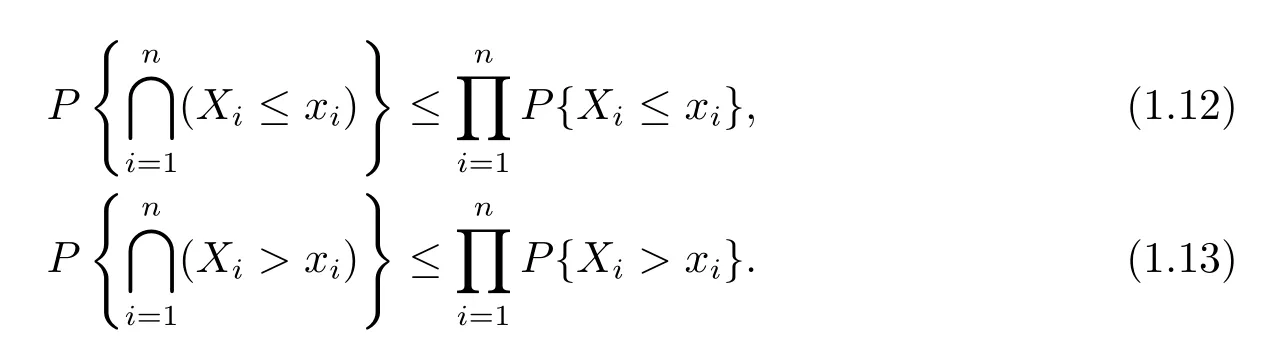
An infinite family of random variables is negatively dependent if every finite subfamily is negatively dependent.
Obviously,negatively associated implies negatively dependent from the definition of negatively associated and negatively dependent.But negatively dependent does not imply negatively associated,so negatively dependent is much weaker than negatively associated.The following lemma is a Rosenthal-type inequality for negatively dependent random variables.
Lemma 1.4[12]Let{Xn,n≥1}be a sequence of negatively dependent random variables with EXn=0 and E|Xn|p<∞for any n≥1,p≥1.Then there exist constants Cp>0 and Dp>0 depending only on p such that,
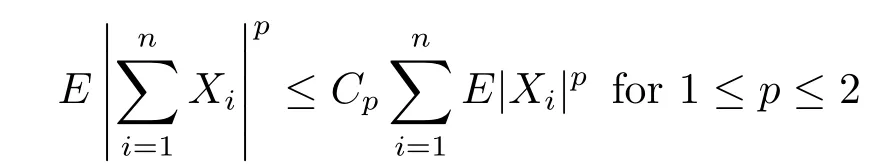
and

Let{Xn,n≥1}be a sequence of random variables defined on probability space (Ω,F,P).For any S?N,letFS=σ(Xk,k∈S).Define the ρ?-mixing coefficients by
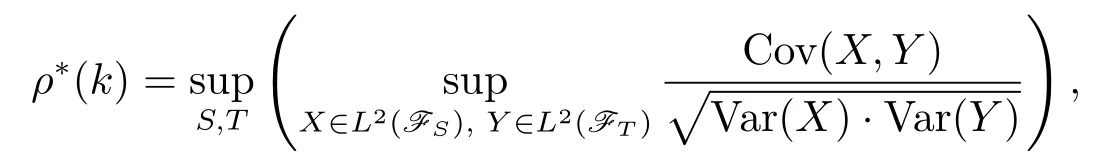
where S,T are the finite subsets of positive integers such that dist(S,T)≥k.We call {Xn,n≥1}a ρ?-mixing sequence if there exists k≥1 such that ρ?(k)<1.
Note that if{Xn,n≥1}is a sequence of independent random variables,then ρ?(n)=0 for all n≥1.
The following lemma is a Rosenthal-type inequality for ρ?-mixing random variables.
Lemma 1.5[13,14]Let{Xn,n≥1}be a sequence of ρ?-mixing random variables, Yn∈σ(Xn),EYn=0,E|Yn|p<∞,n≥1,p≥1.Then there exist constants Cp>0 and Dp>0 depending only on p,k and ρ?(k)where ρ?(k)<1 such that,

and
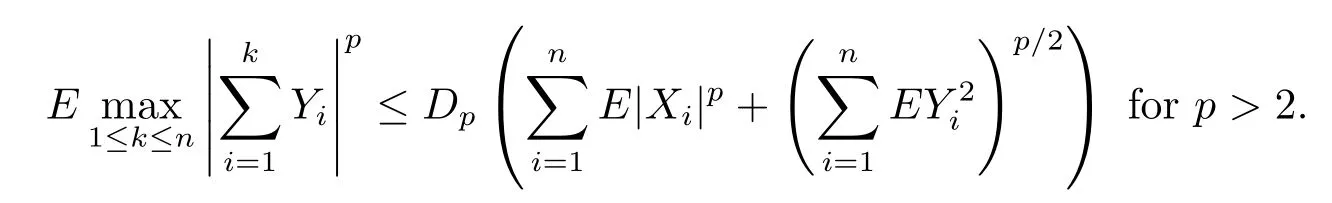
2 Main Results
Theorem 2.1 Suppose that β≥-1.Let{Xni,i≥1,n≥1}be an array of rowwise negatively associated random variables which are stochastically dominated by a random variable X satisfying E|X|p<∞for some p>1.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and
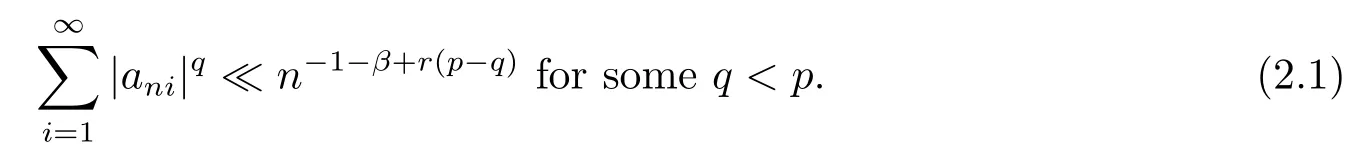
Furthermore,assume that

if p≥2.Let EXni=0 for all i≥1 and n≥1.Then

Proof Without loss of generality,we can assume that ani>0,1≤i≤n,n≥1 (otherwise,we useandinstead of ani,resp.,and note that ani=(1.1)and(2.1),without loss of generality,we can assume that

For any i≥1,n≥1,let
Noting that EXni=0,>1)for any i≥1,n≥1,we have
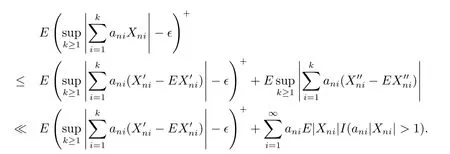
Therefore
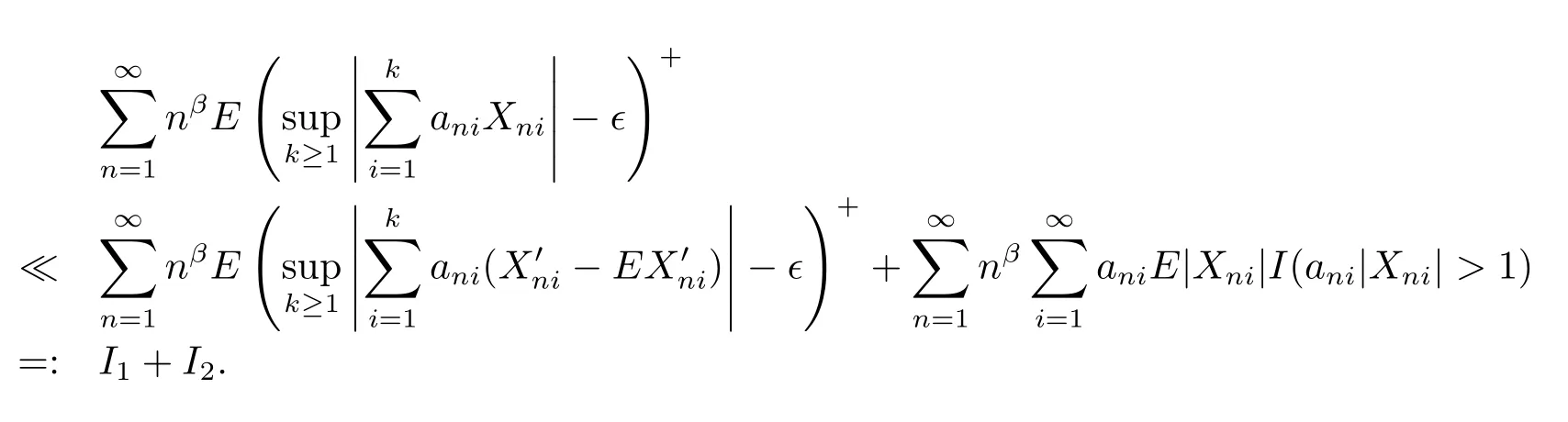
Hence,in order to prove(2.3),it suffices to prove that I1<∞and I2<∞.Take δ>0 suchthat p-δ>max(1,q).By Lemma 1.1,Lemma 1.2 and(2.4),we get that
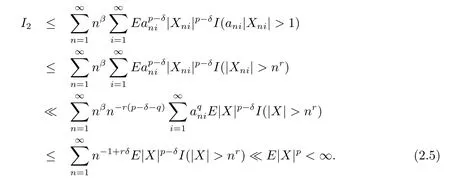
Next,we will prove I1<∞.Noting that p>1,for any M≥p,we obtain by Markov's inequality that
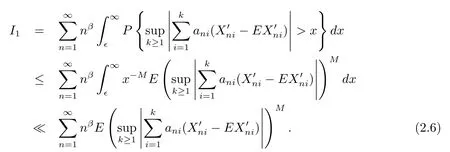
Case 1(1<p<2).Taking δ>0 such that p+δ<2,we get by Lemma 1.1,Lemma 1.3,Crinequality,(2.5)and(2.6)that
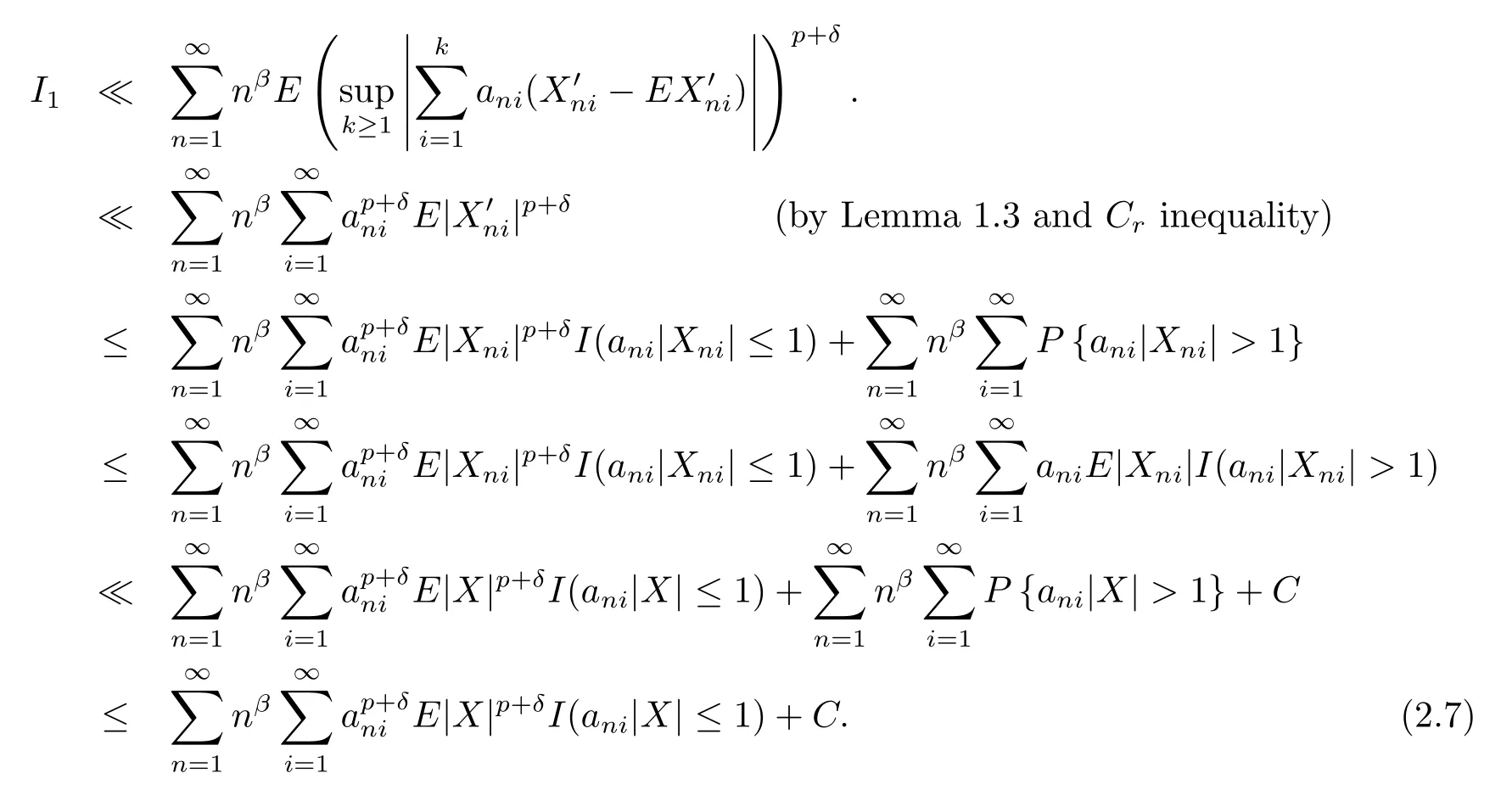
Set Inj={i,(n(j+1))-r<ani≤(nj)-r},j=1,2,···.Then∪j≥1Inj={1,2,···,}.Note also that for all k≥1,n≥1,M≥q,

Hence we have

Note that for any p>1,δ>0,
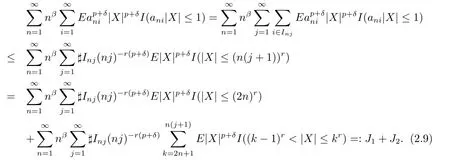
By Lemma 1.2 and(2.8),we obtain that
By(2.8),
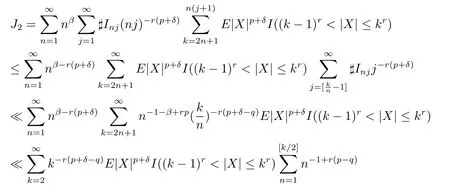
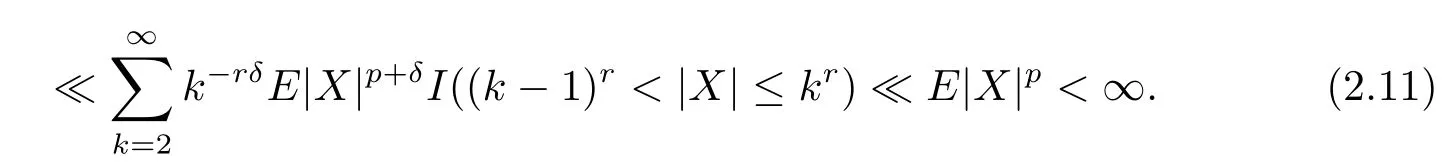
By(2.9),(2.10)and(2.11),for any p>1,δ>0,we have

Combining with(2.7),we get that I1<∞.
Case 2(p≥2).Taking sufficient large δ>0 such that β-α(p+δ)/2<-1,we get by Lemma 1.3,(2.6)and Crinequality that

From the proof of(2.7)and(2.12),we see that I11<∞.Since E|X|p<∞,p≥2 implies EX2<∞,by(2.2),we obtain that
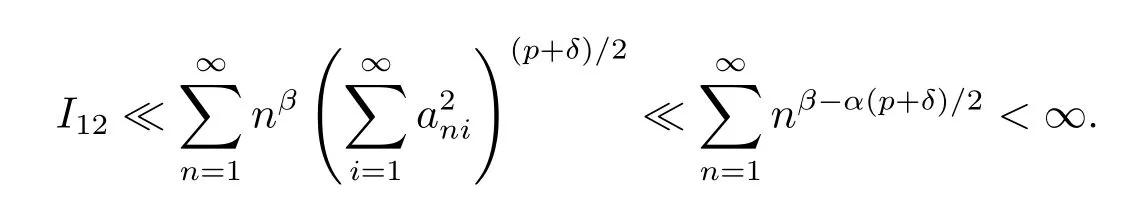
Thus I1<∞.
Remark 2.1 As in Remark 2.3 of Guo and Zhu[6],(2.3)implies(1.7).Hence,when θ+(1+μ+β)/r>1,Theorem 1.1 follows from Theorem 2.1 by taking p=θ+(1+μ+β)/r,q= θ,since

Hence conditions(1.1)and(2.1)are weaker than conditions(1.1)and(1.2).Theorem 2.1 not only extends the result of Volodin et al.[3]and Chen et al.[4]for independent random variables to negatively associated case,but also obtains the weaker sufficient condition of complete moment convergence of the supremum of partial sums for arrays of negatively associated random variables.
Remark 2.2 If 1+μ+β>0,Theorem 1.2,Theorem 1.3 follow from Theorem 2.1 by taking p=1+(1+μ+β)/r,q=1.Theorem 2.1 extends the result of Sung[5]and Guo and Zhu[6].Moreover,the method used for proving our main results is different from that of Sung[5].Our method can be used efficiently to the field of the complete moment convergence for sequences of dependent random variables.
Note that conditions(1.1)and(2.1)together imply

The following theorem shows that if the moment condition of Theorem 2.1 is replaced by a stronger condition E|X|plog|X|<∞,then condition(2.1)can be replaced by the weaker condition(2.13).
Theorem 2.2 Suppose that β≥-1.Let{Xni,i≥1,n≥1}be an array of rowwise negatively associated random variables which are stochastically dominated by a random variable X satisfying E|X|plog|X|<∞for some p≥1.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and(2.13).Furthermore,assume that(2.2)holds for some α>0 if p≥2.Let EXni=0 for all i≥1 and n≥1.Then(2.3)holds.
Proof Applying the same notation and method of Theorem 2.1,we need only to give the different parts.Noting that?logk and p≥1,we have

Set Inj={i,(n(j+1))-r<ani≤(nj)-r},j=1,2,···.Note that for all k≥1,n≥1,M≥p,

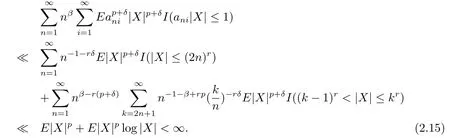
The rest of the proof is the same as that of Theorem 2.1 and is omitted.
Corollary 2.1 Suppose that β≥-1.Let{Xni,i≥1,n≥1}be an array of rowwise negatively associated random variables which are stochastically dominated by a random variable X.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and(1.2)for some θ andμsuch thatμ<2r and 1≤θ<min{2,2-μ/r}.Furthermore,assume that EXni=0 for all i≥1 and n≥1.If
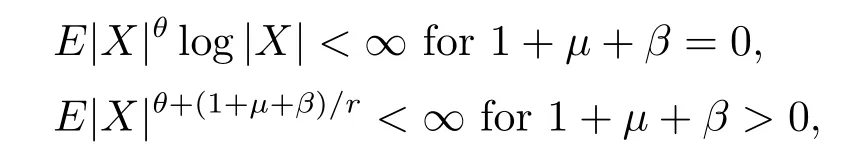
then(2.3)holds.
Proof If 1+μ+β=0,we take p=θ in Theorem 2.2.If 1+μ+β>0,we take p=θ+(1+μ+β)/r,q=θ in Theorem 2.1.Hence(2.3)holds by Theorem 2.1 and Theorem 2.2.
Remark 2.3 Corollary 2.1 extends the result of Sung[5]and Guo and Zhu[6]for θ=1 to 1≤θ<2.
The following theorems extend Theorem 1.1 to negatively dependent random variables. The proof is the same as that of Theorem 2.1 and Theorem 2.2 except that we use Lemma 1.4 instead of Lemma 1.3.
Theorem 2.3 Suppose that β≥-1.Let{Xni,i≥1,n≥1}be an array of rowwise negatively dependent random variables which are stochastically dominated by a random variable X satisfying E|X|p<∞for some p>1.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and(2.1).Furthermore,assume that(2.2)holds for some α>0 if p≥2.Let EXni=0 for all i≥1 and n≥1.Then
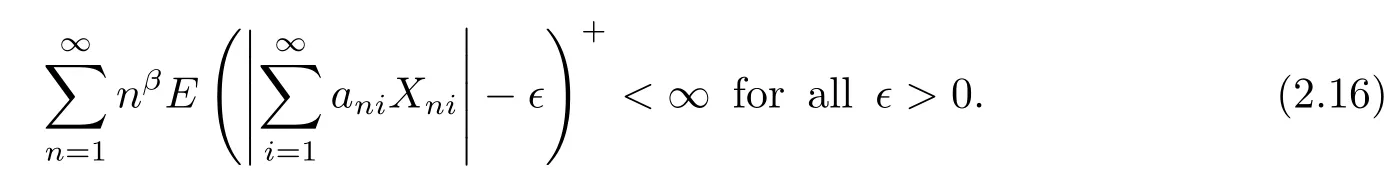
Theorem 2.4 Suppose that β≥-1.Let{Xni,i≥1,n≥1}be an array of rowwise negatively dependent random variables which are stochastically dominated by a random variable X satisfying E|X|plog|X|<∞for some p≥1.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and(2.13).Furthermore,assume that(2.2)holds for some α>0 if p≥2.Let EXni=0 for all i≥1 and n≥1.Then(2.16)holds.
Remark 2.4 If 1+μ+β=0,we take p=θ in Theorem 2.4.If 1+μ+β>0,we take p=θ+(1+μ+β)/r,q=θ in Theorem 2.3.Therefore Theorem 1.4 follows from Theorem 2.3 and Theorem 2.4.However,Theorem 1.4 does not deal with the case of β=-1.Our result covers the case of β=-1.
If the array{Xni,i≥1,n≥1}in Theorem 2.1 and Theorem 2.2 is replaced by the sequence{Xn,n≥1}then we can extend Theorem 1.1 to ρ?-mixing random variables.
Theorem 2.5 Suppose that β≥-1.Let{Xi,i≥1}be a sequence of rowwise ρ?-mixing random variables which are stochastically dominated by a random variable Xsatisfying E|X|p<∞for some p>1.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and(2.1).Furthermore,assume that(2.2)holds for some α>0 if p≥2. Let EXi=0 for all i≥1.Then
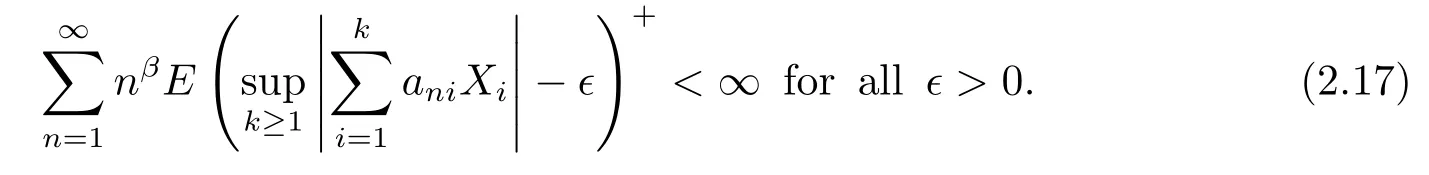
Proof For any i≥1,n≥1,let Xni=XiI(|aniXi|≤1).Note that

The rest of the proof is the same as that of Theorem 2.1 except that we use Lemma 1.5 instead of Lemma 1.3 and it is omitted.
Theorem 2.6 Suppose that β≥-1.Let{Xi,i≥1}be a sequence of rowwise ρ?-mixing random variables which are stochastically dominated by a random variable X satisfying E|X|plog|X|<∞for some p≥1.Let{ani,i≥1,n≥1}be an array of constants satisfying(1.1)and(2.13).Furthermore,assume that(2.2)holds for some α>0 if p≥2.Let EXi=0 for all i≥1.Then(2.17)holds.
Proof For any i≥1,n≥1,let Xni=XiI(|aniXi|≤1).Note that
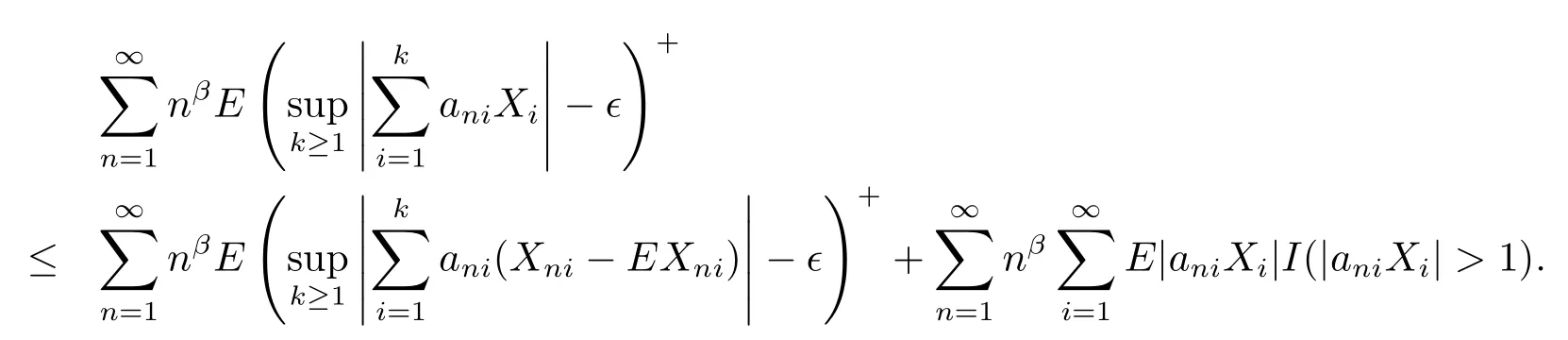
The rest of the proof is the same as that of Theorem 2.2 except that we use Lemma 1.5 instead of Lemma 1.3 and it is omitted.
Remark 2.5 As in Remark 3.7 of Sung[5],Theorem 2.5 and Theorem 2.6 can not be extended to the array{Xni,i≥1,n≥1}of rowwise ρ?-mixing random variables by using the method of the proof of Theorem 2.1 and Theorem 2.2.
References
[1]Hsu P L,Robbins H.Complete convergence and the law of large numbers[J].Proc.Nat.Acad.Sci. USA,1947,33:25-31.
[3]Volodin A,Giuliano Antonini R,Hu T C.A note on the rate of complete convergence for weighted sums of arrays of Banach space valued random elements[J].Lobachevskii J.Math.,2004,15:21-33.
[4]Chen P,Sung S H,Volodin A I.Rate of complete convergence for arrays of Banach space valued random elements[J].Sib.Adv.Math.,2006,16:1-14.
[5]Sung S H.On complete convergence for weighted sums of arrays of dependent random variables[J]. Abstr.Appl.Anal.,2011,2011:11.
[6]Guo Mingle,Zhu Dongjin.On complete moment convergence of weighted sums for arrays of rowwise negatively associated random variables[J].J.Prob.Stat.,2012,2012:12.
[7]Wu,Qunying.A complete convergence theorem for weighted sums of arrays of rowwise negatively dependent random variables[J].J.Inequ.Appl.,2012,2012:50.
[8]Alam K.,Saxena K M L.Positive dependence in multivariate distributions[J].Comm.Stat.The. Meth.A,1981,10:1183-1196.
[9]Joag-Dev K,Proschan F.Negative association of random variables with applications[J].Ann.Stat., 1983,11:286-295.
[10]Shao Qiman.A comparison theorem on moment inequalities between negatively associated and independent random variables[J].J.Theoret.Prob.,2000,13:343-356.
[11]Lehmann E L.Some concepts of dependence[J].Ann.Math.Stat.,1966,37:1137-1153.
[12]Asadian Fakoor N V,Bozorgnia A.Rosenthal’s type inequalities for negatively orthant dependent random variables[J].J.Iranian Stat.Soc.,2006,5:66-75.
[13]Yang Sanchao.Some moment inequalities for partial sums of random variables and their applications[J].Chinese Sci.Bull.,1998,43:1823-1827.
[14]Utev S,Peligrad M.Maximal inequalities and an invariance principle for a class of weakly dependent random variables[J].J.Theoret.Prob.,2003,16:101-115.
相依隨機(jī)變量陣列加權(quán)和的矩完全收斂性
郭明樂,戴鈺,張立君
(安徽師范大學(xué)數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽蕪湖241003)
本文研究了相依隨機(jī)變量陣列加權(quán)和的矩完全收斂性.利用矩不等式和截尾法,建立了相依隨機(jī)變量陣列加權(quán)和的矩完全收斂性的充分條件.將Volodin等(2004)及陳平炎等(2006)的關(guān)于獨(dú)立隨機(jī)變量陣列的結(jié)果推廣到了負(fù)相協(xié)和負(fù)相依隨機(jī)變量陣列的情形,推廣并完善了Sung(2011),吳群英(2012)及郭明樂和祝東進(jìn)(2012)的結(jié)果.
負(fù)相協(xié);負(fù)相依;ρ?混合;矩完全收斂性;完全收斂性
MR(2010)主題分類號(hào):60F15O211.4
?date:2013-12-16Accepted date:2014-09-10
Supported by the National Natural Science Foundation of China(11271020; 11201004);the Key Project of Chinese Ministry of Education(211077);the Natural Science Foundation for Colleges and Universities in Anhui Province(KJ2014A083);the Anhui Provincial Natural Science Foundation(1508085MA11).
Biography:Guo Mingle(1978-),male,born at Fengyang,Anhui,associated professor,major in probability limit theory.
- 數(shù)學(xué)雜志的其它文章
- ENDOMORPHISM ALGEBRAS IN THE YETTER-DRINFEL'D MODULE CATEGORY OVER A REGULAR MULTIPLIER HOPF ALGEBRA
- CHEN-RICCI INEQUALITIES FOR SUBMANIFOLDS OF GENERALIZED COMPLEX SPACE FORMS WITH SEMI-SYMMETRIC METRIC CONNECTIONS
- ON CONFORMABLE NABLA FRACTIONAL DERIVATIVE ON TIME SCALES
- BOUNDEDNESS FOR SOME SCHRDINGER TYPE OPERATORS ON MORREY SPACES WITH VARIABLE EXPONENT RELATED TO CERTAIN NONNEGATIVE POTENTIALS
- STABILITY AND HOPF BIFURCATION OF A PREDATOR-PREY BIOLOGICAL ECONOMIC SYSTEM
- GROUND STATE SOLUTIONS FOR NONLINEAR DIFFERENCE EQUATIONS WITH PERIODIC COEFFICIENTS

