MAI A-li,SUN Guo-wei

(Department of Applied Mathematics,Yuncheng University,Yuncheng 044000,China)

GROUND STATE SOLUTIONS FOR NONLINEAR DIFFERENCE EQUATIONS WITH PERIODIC COEFFICIENTS

MAI A-li,SUN Guo-wei

(Department of Applied Mathematics,Yuncheng University,Yuncheng 044000,China)

In this paper,we study the existence of ground state solutions for nonlinear second order difference equations with periodic coefficients.Using the critical point theory in combination with the Nehari manifold approach,the existence of ground state solutions is established.Under a more general super-quadratic condition than the classical Ambrosetti-Rabinowitz condition,the results considerably generalize some existing ones.Finally,an example is also presented to demonstrate our results.

nonlinear difference equations;Nehari manifold;ground state solutions;critical point theory

2010 MR Subject Classification:39A10;39A12

Document code:AArticle ID:0255-7797(2016)06-1173-10

1　Introduction

In this paper,we consider the following nonlinear second order difference equation

where a(k),b(k)and f(k,u)are T-periodic in k,f(k,u):Z×R→R is a continuous function on u.The forward difference operator?is defined by

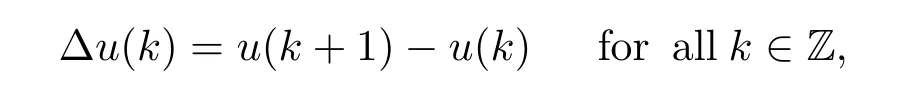
where Z and R denote the sets of all integers and real numbers,respectively.

The solutions of(1.1)are referred to as homoclinic solutions of the equation

In the theory of differential equations,homoclinic orbits play an important role in analyzing the chaos of dynamical systems.If a system has the transversely intersected homoclinic orbits,then it must be chaotic.If a system has the smoothly connected homoclinic orbits, then it can not stand the perturbation,its perturbed system probably produces chaotic. Therefore,it is of practical importance and mathematical significance to study the existence of homoclinic solutions.

Difference equations represent the discrete counterpart of ordinary differential equations. The classical methods are used in difference equations,such as numerical analysis,fixed point methods,linear and nonlinear operator theory,see[1-4].In recent years,the existence and multiplicity of homoclinic solutions for difference equations have been studied in many papers by variational methods,see[5-12]and the reference therein.

Assume the following conditions hold:

(A)a(k)＞0 and a(k+T)=a(k)for all k∈Z.

(B)b(k)＞0 and b(k+T)=b(k)for all k∈Z.

(H1)f∈C(Z×R,R),and there exist C＞0 and p∈(2,∞)such that

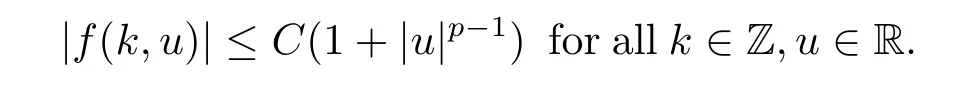
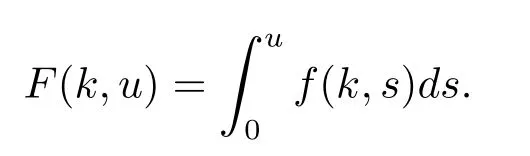
Remark 1.1(H2)implies that u(k)≡0 is a trivial solution of(1.1).

Our main result is following.

Theorem 1.1Suppose that conditions(A),(B)and(H1)-(H4)are satisfied.Then equation(1.1)has at least a nontrivial ground state solution,i.e.,solution corresponding to the least energy of the action functional of(1.1).

Remark 1.2 In[6],the authors also considered(1.1)and assumed that(H2)and the following classical Ambrosetti-Rabinowitz superlinear condition(see[16,17]):there exists a constantμ＞2 such that

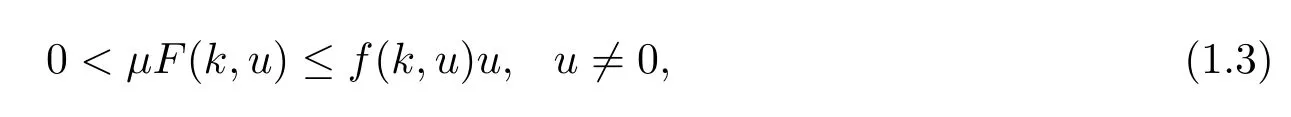
(1.3)implies that for each k∈Z,there exists a constant C＞0 such that

This implies(H3)holds.There exists a superlinear function,such as

does not satisfy(1.3).However,it satisfies the conditions(H1)-(H4).So our conditions are weaker than conditions presented in[6].And in our paper,we do not need periodic approximation technique to obtain homoclinic solutions.Furthermore,the existence of ground state solutions can be obtained.

Remark 1.3In[13],the authors considered the following difference equation

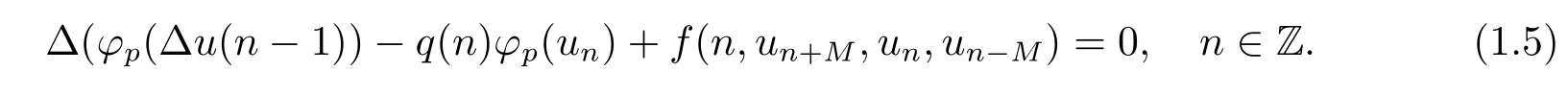
Let p=0 and M=0,(1.2)is the special case of(1.5).

The following hypotheses with p=0 and M=0 are satisfied in[13]:

(F1)F∈C(Z×R,R)with F(n+T,u)=F(n,u)and it satisfies=f(n,u);

(F2)there exist positive constantsand a＜such that|F(n,u)|≤a|u|2for all n∈Z and|u|≤

(F3)there exist constants ρ,c＞and b such that F(n,u)≥c|u|2+b for all n∈Z and|u|≥ρ;

(F4)fu-2F＞0 for all n∈Z and|u|0;

(F5)fu-2F→∞,as|u|→∞.

Note that(H2)-(H4)imply that(F2)-(F4).A nontrivial homoclinic orbit of(1.5)is obtained by Mountain Pass lemma in combination with periodic approximations in[13]. However,in our paper,we employ the Nehari manifold approach instead of periodic approximation technique to obtain the ground state solutions.Furthermore,we show that the functional is coercive on Nehari manifold(Lemma 3.2),which is weaker than P.S.condition in[13].

The rest of this paper is organized as follows.In Section 2,we establish the variational framework associated with(1.1),and transfer the existence of solutions of boundary value problem(1.1)into the existence of critical points of the corresponding functional.By employing the critical point theory,we give proofs of the main results in Section 3.Finally,we give a simple example to demonstrate our results.

2　Variational Framework

In this section,we firstly establish the corresponding variational setting associated with (1.1).Let

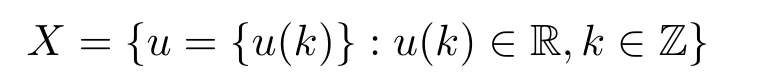
be the set of all real sequences

Then X is a vector space with au+bv={au(k)+bu(k)}for u,v∈X,a,b∈R.

Define the space

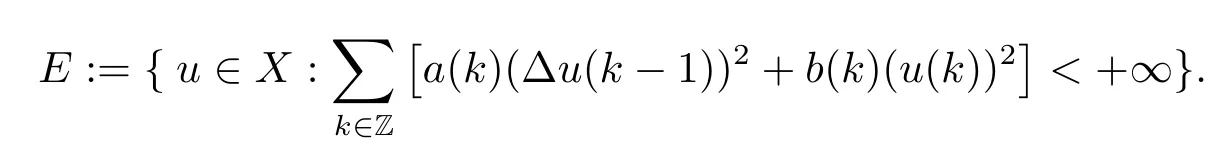
Then E is a Banach space equipped with the corresponding norm

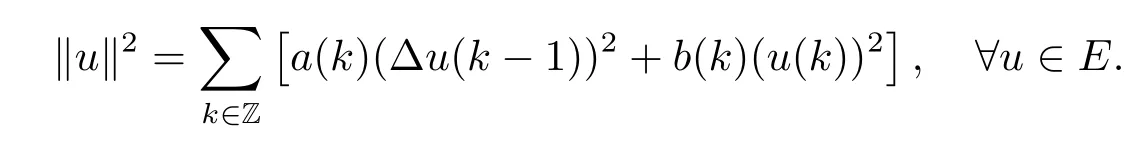
For 1≤p＜+∞,denote

equipped with the norm

|·|is the usual absolute value in R.Then the following embedding between lpspaces holds

Now we consider the variational functional J defined on E by

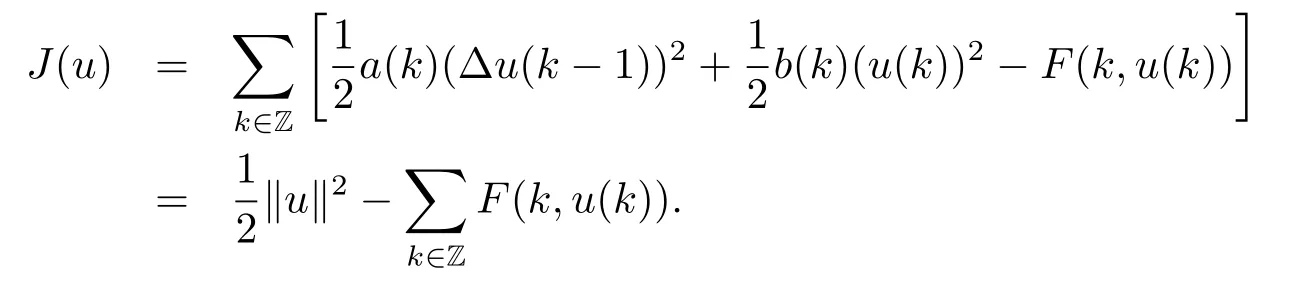
Then J∈C1(E,R),and for all u,v∈E,we have

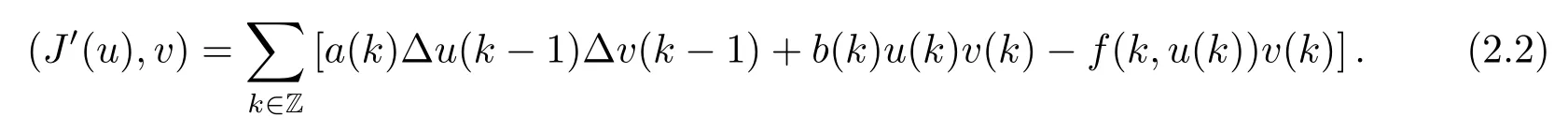
Then we easily get the variational formulation for(1.1).

Lemma 2.1 Every critical point u∈E of J is a solution of(1.1).

Proof We assume that u∈E is a critical point of J,then J＇(u)=0.According to (2.2),this is equivalent to

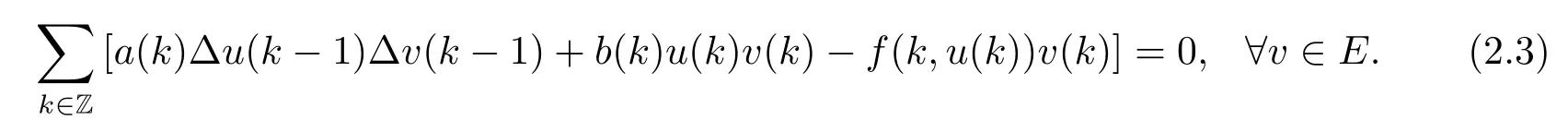
For any h∈Z,we define eh∈E by putting eh(k)=δhkfor all k∈Z,where δhk=1 if h=k;δhk=0 if hk.If we apply(2.3)with v=eh,then

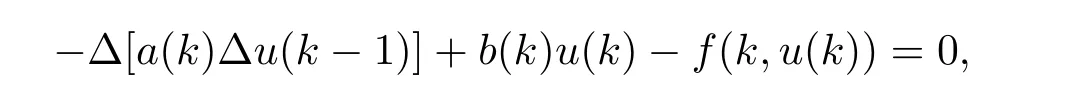
i.e.,u is a solution of(1.1).The proof is completed.

3　Proof of Main Results

Now,we consider the Nehari manifold N={u∈E{0}:J＇(u)u=0},and let c=J(u).By the definition of N,we know N contains all nontrivial critical points of J.

Lemma3.1Assume that(A),(B)and(H2)-(H4)are satisfied,then N is homeomorphic to the unit sphere S in E,where S={u∈E:‖u‖=1}.

Let U?E{0}be a weakly compact subset,we know that

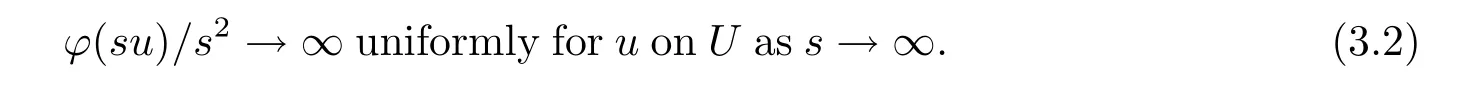
In fact,let{un}?U.It needs to show that

as n→∞.Passing to a subsequence if necessary,un?u∈E{0}and un(k)→u(k)for every k,as n→∞.

Note that from(H2)and(H4),it is easy to get that

Since|snun(k)|→∞and un0,by(H3)and(3.3),we have

Thus we obtain(3.2)holds.

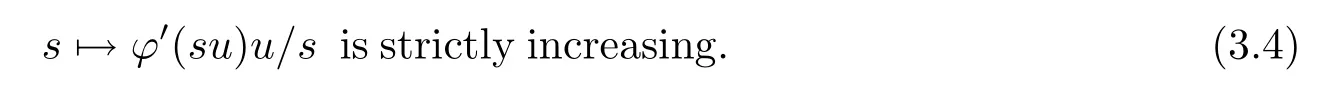
Let h(s):=J(sw),s＞0.Then

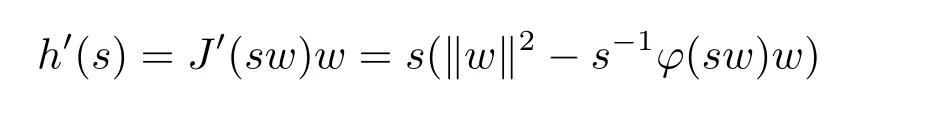
from(3.1)-(3.4),then there exists a unique sw,such that,when 0＜s＜sw,h＇(s)＞0;and when s＞sw,h＇(s)＜0.Therefore h＇(sw)=J＇(sww)w=0 and sww∈N.

Therefore swis a unique maximum of h(s),and we can define the mapping:E {0}→N by setting(w):=sww.Then the mappingis continuous.Indeed,suppose wn→w0.Since(tu)=(u)for each t＞0,we may assume wn∈S for all n.Write(wn)=swnwn.Then{swn}is bounded.If not,swn→∞as n→∞.

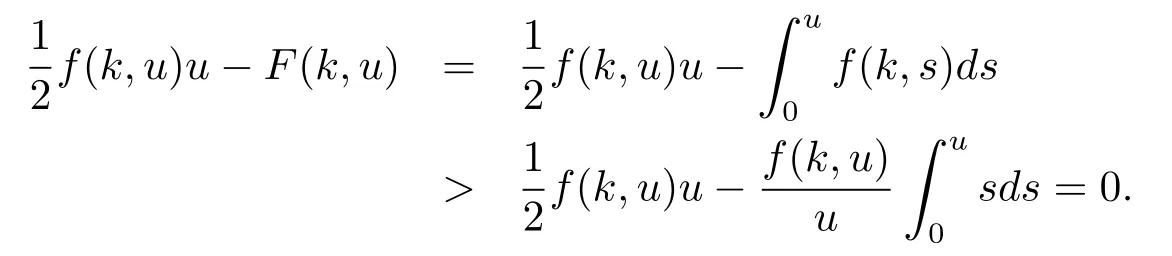
So for all u∈N,we have

By(H3),we have

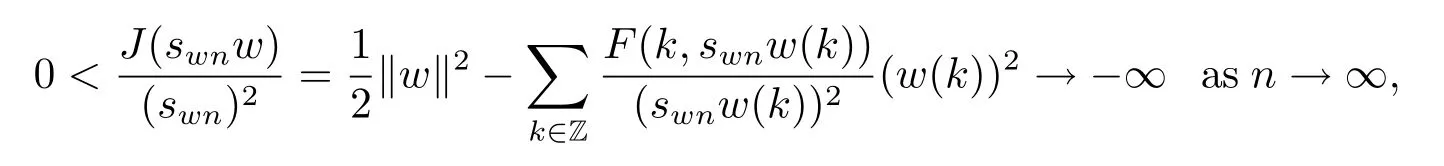
which is a contradiction.Therefore,swn→s＞0 after passing to a subsequence if needed. Since N is closed and(wn)=swnwn→sw,sw∈N.Hence sw=sww=(w)by the uniqueness of sw.

Therefore we define a mapping m:S→N by setting m:=|S,then m is a homeomorphism between S and N.

We also consider the functional:E{0}→R and Ψ:S→R by

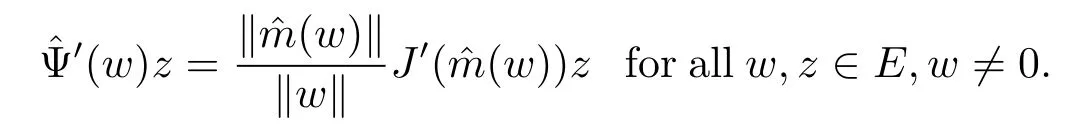
In fact,let w∈E{0}and z∈E.By Lemma 3.1 and the mean value theorem,we obtain

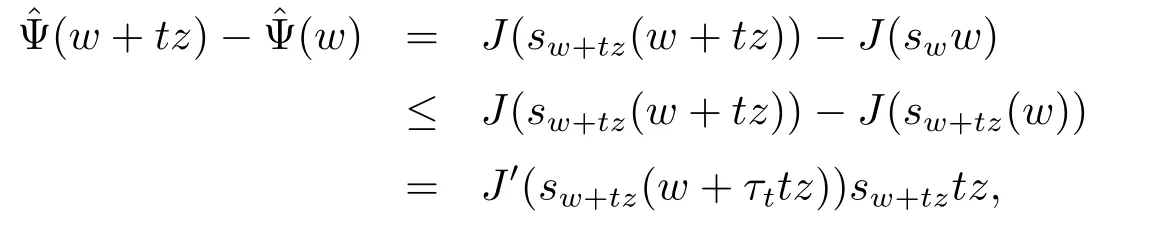
where|t|is small enough and τt∈(0,1).Similarly,

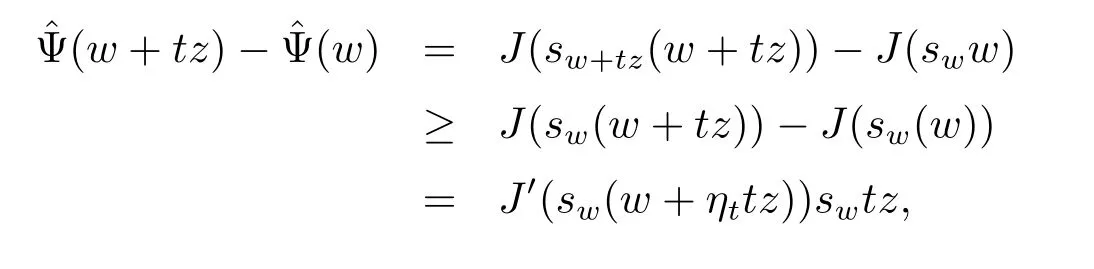
where ηt∈(0,1).Combining these two inequalities and the continuity of function wsw, we have

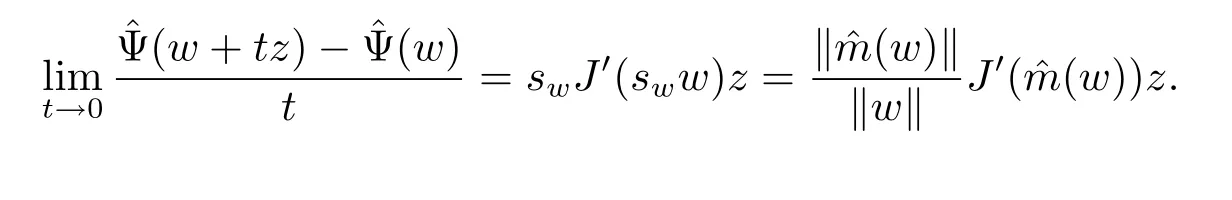
Lemma 3.2 Assume that(A),(B)and(H1)-(H3)are satisfied,for u∈N then J(u)→∞as‖u‖→∞.

Proof By way of contradiction,we assume that there exists a sequence{un}?N such that J(un)≤d,as‖un‖→∞.Set vn=,and then there exists a subsequence,still denoted by vn,such that vn?v,and therefore vn(k)→v(k)for every k,as n→∞.

First we can prove that there exist δ＞0 and kj∈Z such that

In fact,if not,then vn→0 in l∞as n→∞.For q＞2,

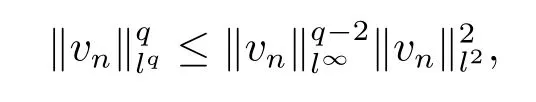
so we have vn→0 in all lq,q＞2.

Note that from(H1)and(H2),we have for any ε＞0,there exists cε＞0 such that

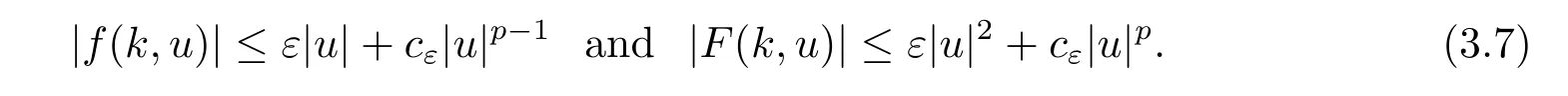
Then for each s＞0,we have

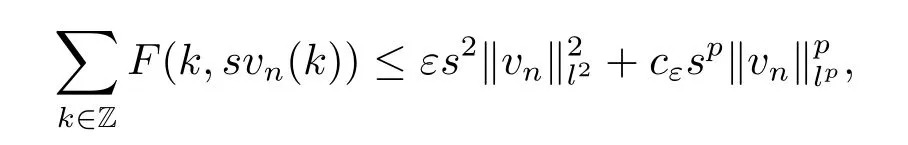
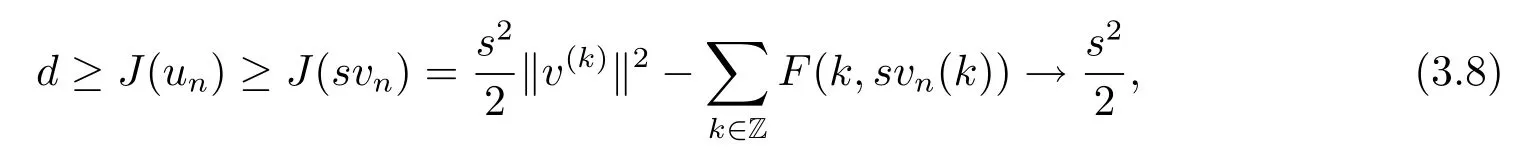
as n→∞.This is a contradiction if s＞

By periodicity of coefficients,we know J and N are both invariant under T-translation. Making such shifts,we can assume that 1≤kj≤T-1 in(3.6).Moreover,passing to a subsequence,we can assume that kj=k0is independent of j.

Next we can extract a subsequence,still denoted by{vn},such that vn(k)→v(k)for all k∈Z.Specially,for k=k0,inequality(3.6)shows that|v(k0)|≥δ,so v0.Since |un(k)|→∞as n→∞,it follows again from(H3)that

a contradiction again.

From above,we have the following lemma,which is important in this paper.

Lemma 3.3{wn}is a Palais-Smale sequence for Ψ if and only if{m(wn)}is a Palais-Smale sequence for J.

Proof Let{wn}be a Palais-Smale sequence for Ψ,and let un=m(wn)∈N.Since for every wn∈S we have an orthogonal splitting E=TwnS⊕Rwn,we have

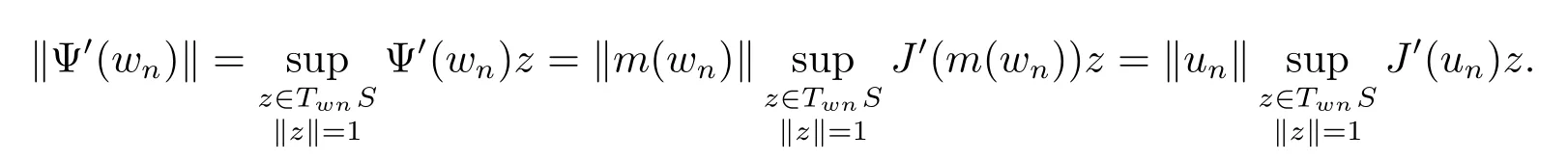
Then

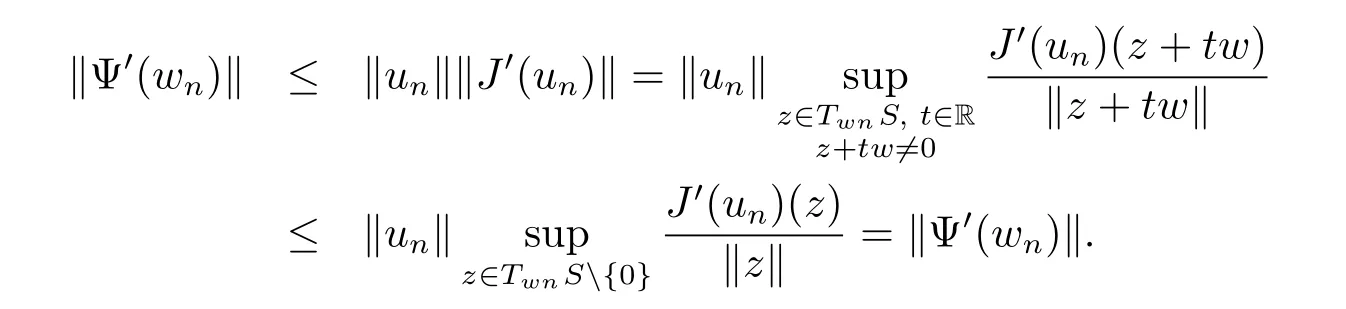
Therefore

By(3.5),for un∈N,J(un)＞0,so there exists a constant c0＞0 such that J(un)＞c0. And since c0≤J(un)=Together with Lemma3.2,≤‖un‖≤supn‖un‖＜∞.Hence{wn}is a Palais-Smale sequence for Ψ if and only if {un}is a Palais-Smale sequence for J.

Now,we give the detailed proof of Theorem 1.1.

Proof From(3.9),Ψ＇(w)=0 if and only if J＇(m(w))=0.So w is a critical point of Ψ if and only if m(w)is a nontrivial critical point of J.Moreover,the corresponding values of Ψ and J coincide and infSΨ=infNJ.

Let u0∈N such that J(u0)=c,then m-1(u0)∈S is a minimizer of Ψ and therefore a critical point of Ψ,so u0is a critical point of J.It needs to show that there exists a minimizer u∈N of J|N.

Let{wn}?S be a minimizing sequence for Ψ.By Ekeland's variational principle we may assume Ψ(wn)→c,Ψ＇(wn)→0 as n→∞,hence J(un)→c,J＇(un)→0 as n→∞, where un:=m(wn)∈N.

It follows from Lemma 3.2 that{un}is bounded in N,then there exists a subsequence, still denoted by the same notation,such that unweakly converges to some u∈E.We know that there exist δ＞0 and kj∈Z such that

If not,then un→0 in l∞as n→∞.Note that,for q＞2,

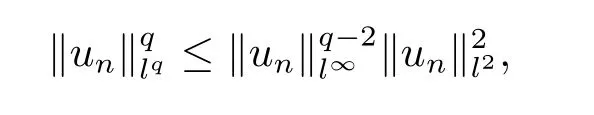
then un→0 in all lq,q＞2.By(3.7),we have

So‖un‖2→0,as n→∞,which contradicts with un∈N.

Since J and J＇are both invariant under T-translation.Making such shifts,we assume that 1≤kj≤T-1 in(3.10).Moreover passing to a subsequence,we assume that kj=k0is independent of j.Extracting a subsequence,still denoted by{un},we have un?u and un(k)→u(k)for all k∈Z.Specially,for k=k0,inequality(3.10)shows that|u(k0)|≥δ,so u0.Hence u∈N.

Now,we prove that J(u)=c.By Fatou's lemma,

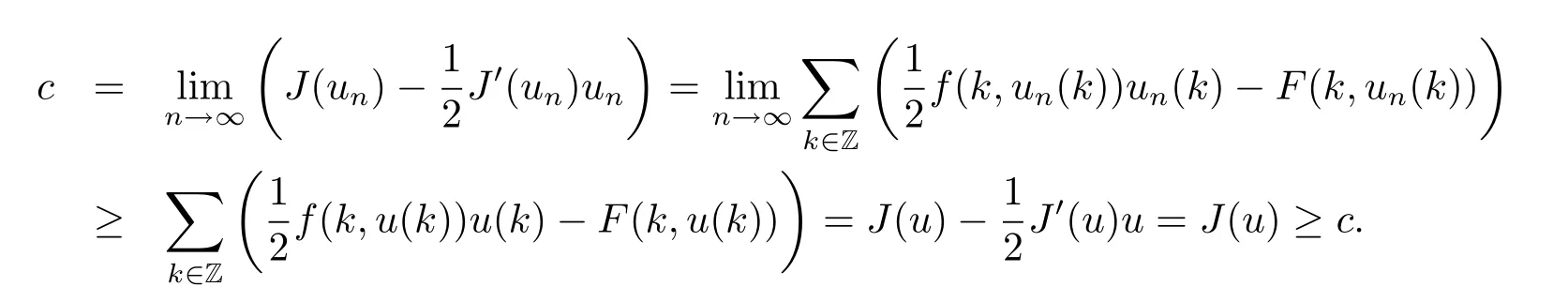
So J(u)=c.The proof of Theorem 1.1 is completed.

Example 1Consider the difference equation

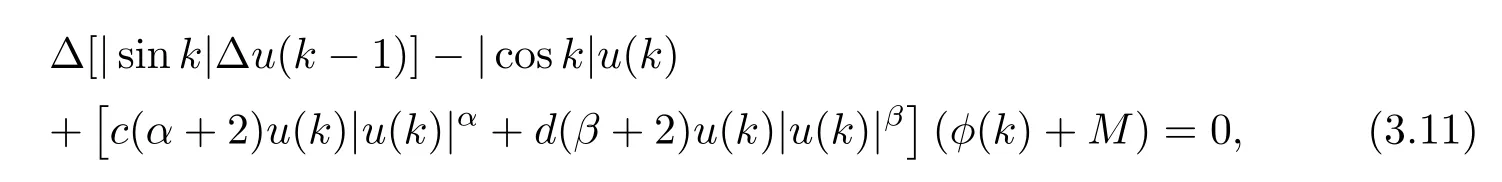
where c＞0,d＞0,α≥β＞0,M＞0,φ(k)is a bounded continuous π-periodic function and |φ(k)|＜M,k∈Z.Let a(k)=|sink|,b(k)=|cosk|,

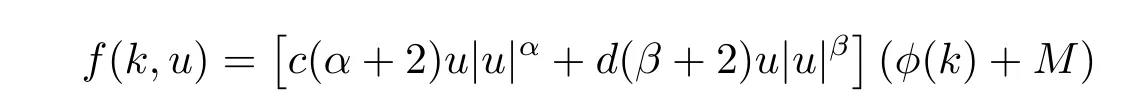
and

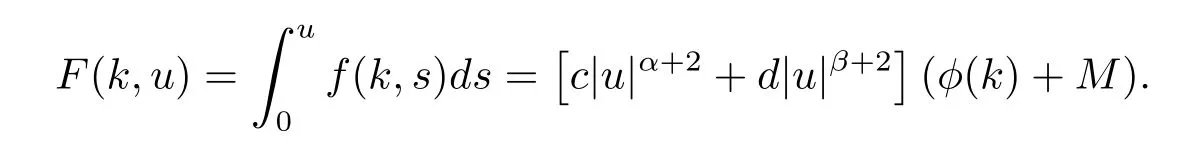
It is easy to show that all the assumptions of Theorem 1.1 are satisfied.Therefore,equation (3.11)has at least one homoclinic solution.

References

[1]Zhang K,Xu J.Existence of solutions for a second order difference boundary value problem[J].J. Math.,2014,34:856-862.

[2]Agarwal R P.Difference equations and inequalities:theory,methods and applications[M].New York: Marcel Dekker,1992.

[3]Kelly W G,Peterson A C.Difference equations:an introduction with applications[M].New York: Academic Press,1991.

[4]Lakshmikantham V,Trigiante D.Theory of difference equations:numerical methods and applications[M].New York:Academic Press,1988.

[5]Ma Manjun,Guo Zhiming.Homoclinic orbits for second order self-adjoint difference equations[J]. J.Math.Anal.Appl.,2005,323:513-521.

[6]Ma Manjun,Guo Zhiming.Homoclinic orbits for nonliear second order difference equations[J].Nonl. Anal.,2007,67:1737-1745.

[7]Ma Defang,Zhou Zhan.Existence and multiplicity results of homoclinic solutions for the DNLS equations with unbounded potentials[J].Abstr.Appl.Anal.,2012,2012:1-15.

[8]Mai Ali,Zhou Zhan.Ground state solutions for the periodic discrete nonlinear Schrdinger equations with superlinear nonlinearities[J].Abstr.Appl.Anal.,2013,2013:1-11.

[9]Mai Ali,Zhou Zhan.Discrete solitons for periodic discrete nonlinear Schrdinger equations[J].Appl. Math.Comput.,2013,222:34-41.

[10]Mai Ali,Zhou Zhan.Homoclinic solutions for a class of nonlinear difference equations[J].J.Appl. Math.,2014,2014:1-8.

[11]Sun Guowei.On standing wave solutions for discrete nonlinear Schrdinger equations[J].Abstr. Appl.Anal.,2013,2013:1-6.

[12]Shi Haiping,Zhang Hongqiang.Existence of gap solitons in periodic discrete nonlinear Schrdinger equations[J].J.Math.Anal.Appl.,2010,361(2):411-419.

[13]Haiping Shi,Xia Liu,Yuanbiao Zhang.Homoclinic orbits for second order p-Laplacian difference equations containing both advance and retardation[J].RACSAM,2016,110(1):65-78.

[14]Szulkin A,Weth T.The method of Nehari manifold[A].Gao D Y,Motreanu D,eds.Handbook of nonconvex analysis and applications[C].Boston:International Press,2010.

[15]Willem M.Minimax theorems[M].Boston:Birkhuser,1996.

[16]Ambrosetti A,Rabinowitz P H.Dual variational methods in critical point theory and applications[J]. J.Funct.Anal.,1973,14:349-381.

[17]Rabinowitz P H.Minimax methods in critical point theory with applications to differential equations[C].Providence RI:AMS,1986.

一類周期非線性差分方程的基態(tài)解

買阿麗,孫國偉

(運城學院應(yīng)用數(shù)學系,山西運城044000)

本文研究了一類二階周期非線性差分方程基態(tài)解的存在性問題.利用臨界點理論結(jié)合Nehari流形方法,獲得了此類方程基態(tài)解的存在性.在比經(jīng)典AR條件更一般的超二次條件下,本文結(jié)論推廣了已有的結(jié)果,并舉例說明此類方程解的存在性.

非線性差分方程;Nehari流形;基態(tài)解;臨界點理論

MR(2010)主題分類號:39A10;39A12O175.1

?date:2015-06-25Accepted date:2016-01-04

Supported by National Natural Science Foundation of China(11526183; 11371313;11401121);the Natural Science Foundation of Shanxi Province(2015021015)and Foundation of Yuncheng University(YQ-2014011;XK-2014035).

Biography:Mai Ali(1981-),femal,born at Yuncheng,Shanxi,associate professor,major in the theory and applications of differential equations.