趙夫群

(陜西咸陽師范學(xué)院 教育科學(xué)學(xué)院, 咸陽　712000)

?

一類新型計(jì)算機(jī)病毒最優(yōu)控制模型?

趙夫群?

(陜西咸陽師范學(xué)院 教育科學(xué)學(xué)院, 咸陽712000)

計(jì)算機(jī)病毒的存在,使得很多計(jì)算機(jī)無法正常運(yùn)行,并造成巨大的損失.針對這種情況,提出一類新型計(jì)算機(jī)病毒的最優(yōu)控制.控制首先對原有的計(jì)算機(jī)病毒模型進(jìn)行改進(jìn),加入控制項(xiàng),提出最優(yōu)控制問題,并證明最優(yōu)控制的存在性,然后利用龐德里亞金的極小值原理進(jìn)行理論分析,最后進(jìn)行數(shù)值模擬.數(shù)值模擬結(jié)果表明,在沒有控制的條件下,原模型得出基本再生數(shù)大于1, 說明存在地方病平衡點(diǎn),并且最終會導(dǎo)致病毒爆發(fā),而數(shù)值模擬揭示,運(yùn)用有效的控制策略能夠更好地抑制計(jì)算機(jī)病毒的傳播.

計(jì)算機(jī)病毒模型,極小值原理,最優(yōu)控制,數(shù)值仿真

引言

計(jì)算機(jī)病毒是指編制者在計(jì)算機(jī)程序中插入的破壞計(jì)算機(jī)功能或者破壞數(shù)據(jù),影響計(jì)算機(jī)使用并且能夠自我復(fù)制的一組計(jì)算機(jī)指令或者程序代碼.計(jì)算機(jī)病毒和醫(yī)學(xué)上的“病毒”不同,計(jì)算機(jī)病毒不是天然存在的,是某些人利用計(jì)算機(jī)軟件和硬件所固有的脆弱性編制的一組指令集或程序代碼.它能通過某種途徑潛伏在計(jì)算機(jī)的存儲介質(zhì)或者程序里,當(dāng)達(dá)到某種條件時即被激活,通過修改其他程序的方法將自己的精確拷貝或者可能演化的形式放入其他程序中.從而感染其他程序,對計(jì)算機(jī)資源進(jìn)行破壞,所謂的病毒就是人為造成的,對其他用戶的危害性很大.計(jì)算機(jī)病毒的破壞性及傳染性對社會造成極大的傷害,僅2008年,計(jì)算機(jī)病毒在全球造成的經(jīng)濟(jì)損失就高達(dá)85億美元.

計(jì)算機(jī)病毒的傳播類似于生物學(xué)中病毒的傳播方式,通過各種渠道從已被感染的計(jì)算機(jī)擴(kuò)散到為被感染的計(jì)算機(jī),導(dǎo)致硬盤數(shù)據(jù)被清空.計(jì)算機(jī)病毒具有自我復(fù)制并傳播給其他計(jì)算機(jī)的功能,同時又有很大的破壞性,一旦計(jì)算機(jī)被感染上病毒,將可能面臨著計(jì)算機(jī)癱瘓,更嚴(yán)重的甚至?xí)斐缮鐣薮蟮慕?jīng)濟(jì)損失,因此有效預(yù)防和控制計(jì)算機(jī)病毒的傳播就顯得尤為重要. 生物病毒的最優(yōu)控制在理論研究方面已經(jīng)取得很大的成就.比如,艾滋病病毒的最優(yōu)控制,乙肝,丙肝病毒的最優(yōu)控制[1-6],由于計(jì)算機(jī)病毒和生物病毒很相似,很多學(xué)者將生物學(xué)病毒和殺毒軟件結(jié)合起來研究計(jì)算機(jī)病毒模型[7-14]. 雖然控制理論被廣泛應(yīng)用到流行病傳播模型中,但是很少學(xué)者有研究將控制理論應(yīng)用到計(jì)算機(jī)病毒模型中,因此有必要研究一下計(jì)算機(jī)病毒的最優(yōu)控制模型.

本文在文獻(xiàn)[14]的基礎(chǔ)上進(jìn)行了改進(jìn),將之前的常數(shù)參數(shù)變量變成時變的控制變量,并為新模型建立了最優(yōu)控制系統(tǒng). 首先給出控制系統(tǒng)的目標(biāo)泛函;然后用Pontryagin極小值原理[15-17]推導(dǎo)出最優(yōu)控制;最后數(shù)值仿真驗(yàn)證了所得結(jié)論.

1　計(jì)算機(jī)病毒模型

1.1計(jì)算機(jī)病毒模型的提出

考慮計(jì)算機(jī)網(wǎng)絡(luò)由若干個節(jié)點(diǎn)組成的,并且所有的未感染的計(jì)算機(jī)都可能受到惡意軟件的攻擊.當(dāng)惡意軟件攻擊計(jì)算機(jī)網(wǎng)絡(luò)時,一部分節(jié)點(diǎn)會被感染.這些感染的節(jié)點(diǎn)又會繼續(xù)感染健康的節(jié)點(diǎn),因此被感染的節(jié)點(diǎn)的數(shù)目會大量增加.殺毒軟件的使用,能夠有效的防治計(jì)算機(jī)病毒的傳播,所以文獻(xiàn)[14]提出了如下的計(jì)算機(jī)模型:

(1)

1.2改進(jìn)的計(jì)算機(jī)病毒模型

由于現(xiàn)實(shí)生活中計(jì)算機(jī)之間也可以進(jìn)行病毒傳播,所以本文在文獻(xiàn)[14]的基礎(chǔ)上增加一項(xiàng)β1SI,得到的改進(jìn)模型如下:

(2)

系統(tǒng)(1)由四部分組成: S表示沒有感染病毒但很容易感染病毒的節(jié)點(diǎn); I表示已經(jīng)感染病毒的節(jié)點(diǎn); M表示網(wǎng)絡(luò)中惡意對象; P表示殺毒軟件. 系統(tǒng)中參數(shù)含義: A表示計(jì)算機(jī)的輸入率,β1表示計(jì)算機(jī)之間病毒感染率,β2表示惡意對象入侵計(jì)算機(jī)的感染率,γ表示殺毒率,d表示斷網(wǎng)率,α表示大量病毒入侵計(jì)算機(jī)癱瘓率,δ表示病毒復(fù)制能力,μ表示病毒入侵率,μ0表示殺惡意對象的效率,η表示殺毒軟件的增長率,η0表示殺毒失敗率,P0表示計(jì)算機(jī)現(xiàn)有的殺毒能力.

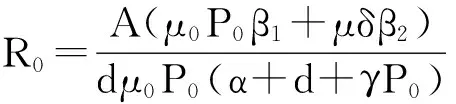
2　最優(yōu)控制問題

系統(tǒng)(1)中γ和μ0是個常數(shù),本文對此再次改進(jìn),將γ和μ0改成控制變量函數(shù)θu(t)和u(t).因?yàn)棣煤挺?是常數(shù)的話,會使得控制的成本大大增加,變成時變的控制變量,可以保證在控制計(jì)算機(jī)病毒減少到很低甚至到零的成本遠(yuǎn)遠(yuǎn)低于常數(shù)變量.帶有控制變量的控制模型如下:

(3)

其中0≤u(t)≤1,θ表示殺毒率調(diào)節(jié)系數(shù),u(t)表示殺毒率,這里假設(shè)殺毒率和購買和更新的殺毒軟件的數(shù)量成正比.

首先,為了建立最優(yōu)控制系統(tǒng),對于給定的整數(shù)T>0,給定下列集合作為控制集:

U={u(t)∈L2(0,T): 0≤u(t)≤1,0≤t≤T}

(4)

其次,目標(biāo)泛函定義如下:

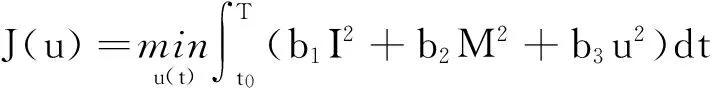
(5)

這樣的目標(biāo)函數(shù)是為了通過控制使得感染的計(jì)算機(jī)和惡意對象的數(shù)量達(dá)到最小,并且系統(tǒng)的消耗最少,從而達(dá)到最優(yōu)控制的目的,這也是符合我們最優(yōu)控制的初衷.

初始條件為:

S(0)=S0, I(0)=I0, M(0)=M0,

P(0)=P0.

(6)

下面給出最優(yōu)控制問題的Lagrangian函數(shù),

L(I,u)=b1I2+b2M2+b3u2,

(7)

其中I,M表示t時刻I和M的數(shù)目,u表示為了減少I和M所付出的系統(tǒng)消耗.例如我們用于購買和更新殺毒軟件所需要的金錢.

為了尋找目標(biāo)泛函式(5)的最小值,先定義Hamiltonian函數(shù)如下:

H=b1I2+b2M2+b3u2+λ1(A-β1SI-β2SM+

θu(t)IP-dS)+λ2(β1SI+β2SM-

θu(t)IP-dI-αI)+λ3(δμI-u(t)MP)+

λ4(ηI-η0(P-P0)).

(8)

3　最優(yōu)控制存在性

最優(yōu)控制的存在性證明:

由文獻(xiàn)[15],且方程(3),(4), (6)滿足如下條件:

1) 控制集和相對應(yīng)的狀態(tài)變量集為非空集合.

2) 可測集U是閉的凸集.

3) 系統(tǒng)(3)方程的右邊關(guān)于u的線性函數(shù),并且是連續(xù)有界的.

4) 目標(biāo)泛函的被積函數(shù)L(I,u)在U上式凹函數(shù).

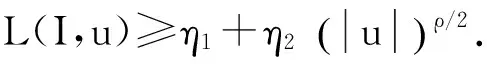
綜述,系統(tǒng)(2)存在最優(yōu)控制.

利用Pontryagin的極小值原理[16],極小值原理的必要條件如下:

7) S(0)=S0,I(0)=I0,M(0)=M0,P(0)=P0.

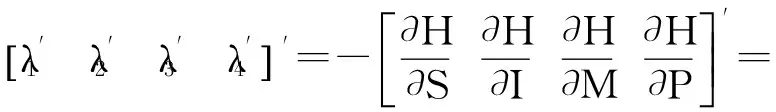
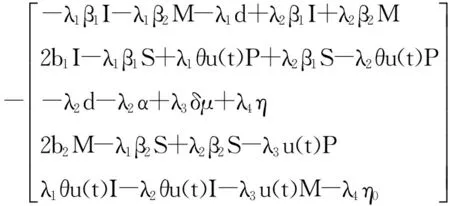
9) λi(T)=0, i=1,2,3,4.

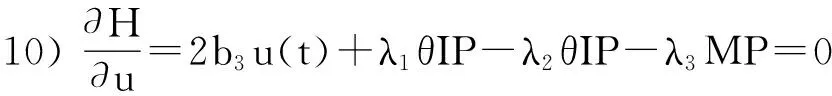
得出使目標(biāo)泛函式(4)到達(dá)最小值的一個最優(yōu)控制為

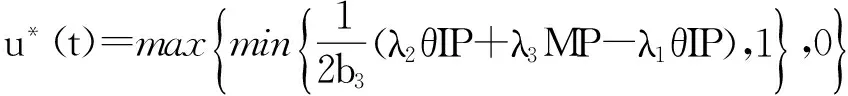
(9)

4　數(shù)值模擬和分析

根據(jù)前面的理論分析,本文通過實(shí)驗(yàn)來驗(yàn)證使用適當(dāng)?shù)目刂撇呗灾?計(jì)算機(jī)病毒傳播將得到有效控制.并將殺毒率分別是常數(shù)和變量函數(shù)進(jìn)行比較,從圖中看出控制模型能夠更加有效地抑制病毒的傳播.

給定初始條件如下:

S(0)=0.2,I(0)=0.3,M(0)=0.3,P(0)=0.2,經(jīng)過對模型的初始條件及相關(guān)參數(shù)進(jìn)行多次試驗(yàn)后,選取了如下參數(shù):

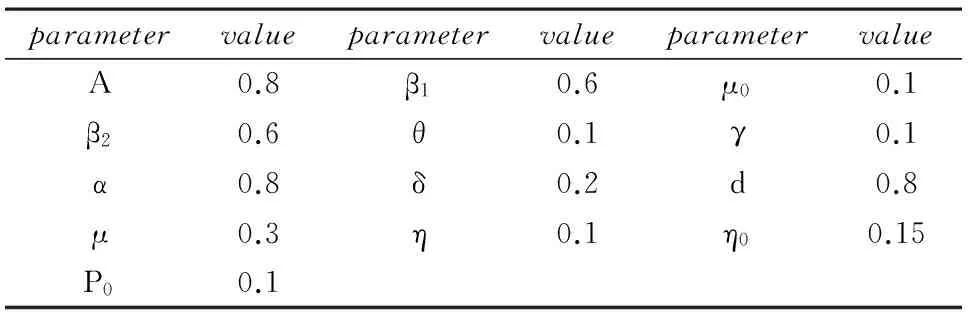
表1　數(shù)值模擬參數(shù)

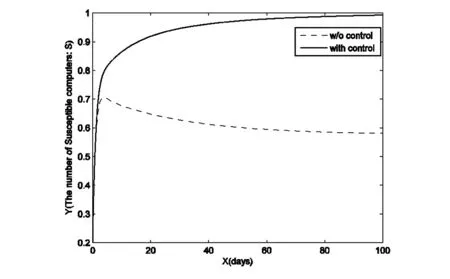
圖1　控制前后易感電腦S的趨勢變化

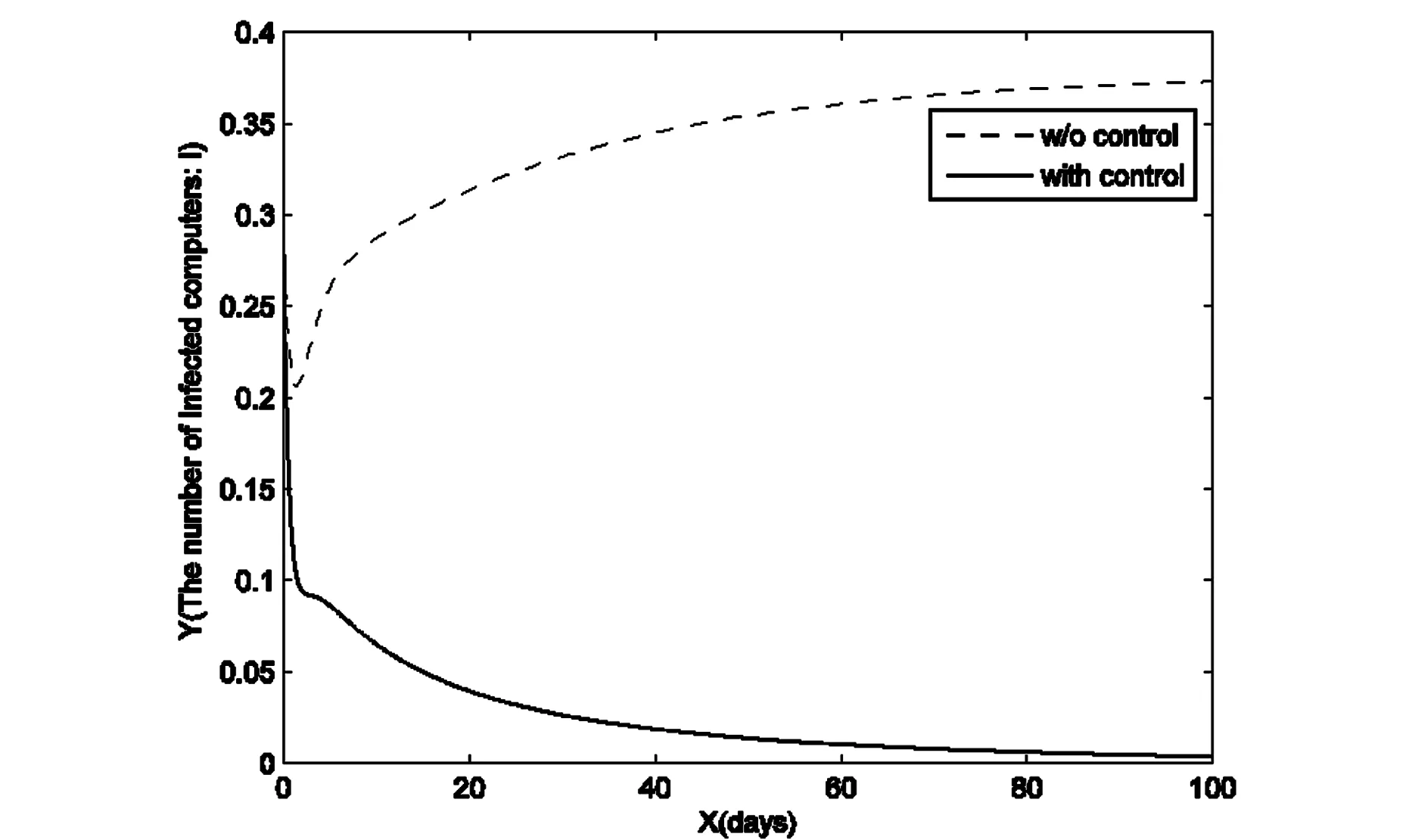
圖2　控制前后被感染的電腦I的趨勢變化Fig.2　The number of infected computers with control and without control

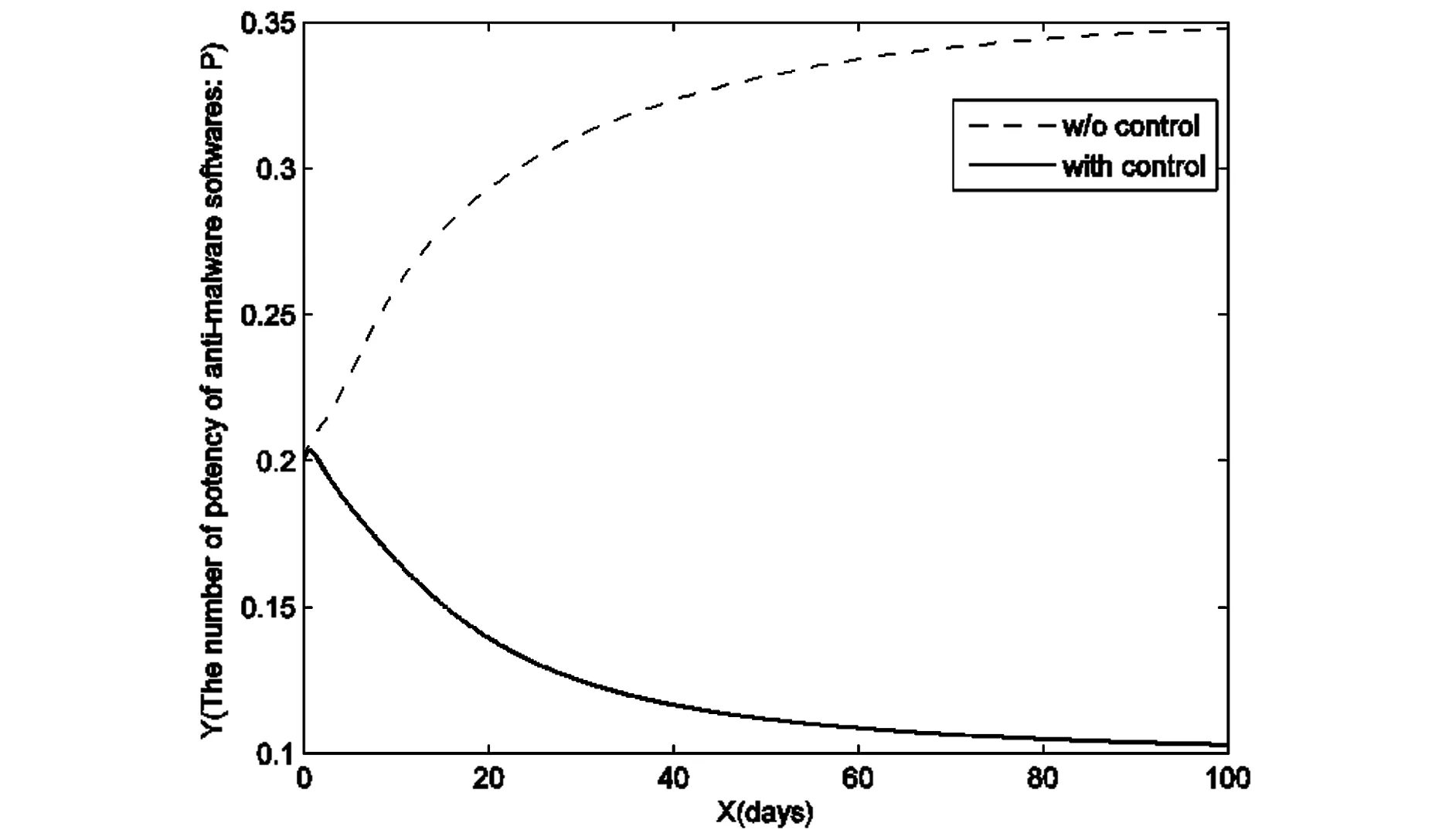
圖4　控制前后殺毒軟件P的趨勢變化Fig.4　The number of anti-malicious software with control and without control

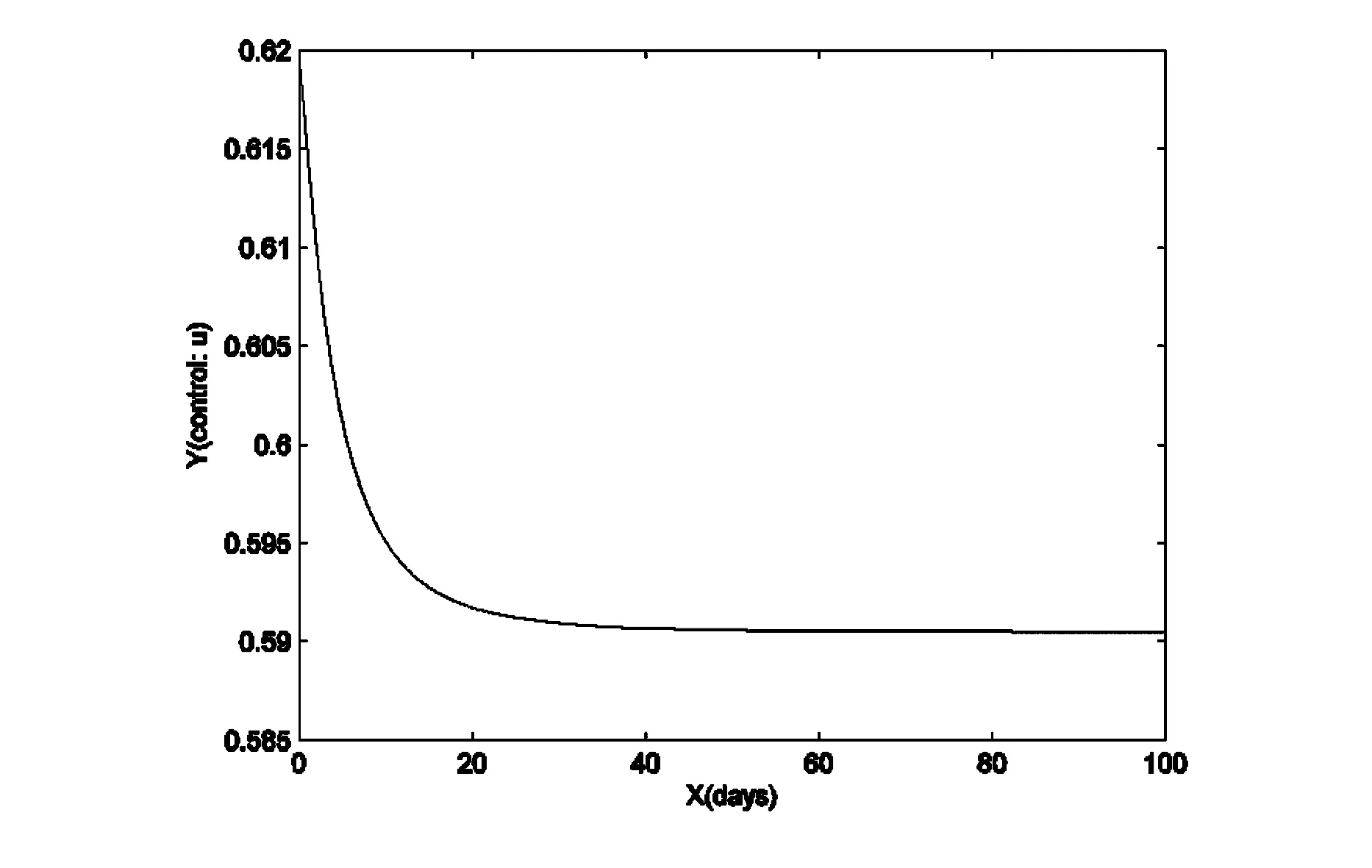
圖5　控制變量曲線

5　結(jié)語

通過上面的數(shù)值模擬可以很明顯的看到,在有最優(yōu)控制條件下,易感染的計(jì)算機(jī)的數(shù)量和被感染的計(jì)算機(jī)的數(shù)量趨勢是符合目標(biāo)函數(shù)的預(yù)期,而在沒有控制的條件下,計(jì)算機(jī)病毒的傳播無法被控制.從控制量的走勢也可以明顯看到,并不需要一直持續(xù)的最大效力就可以將計(jì)算機(jī)病毒的傳播控制住,這也是符合最優(yōu)控制的目標(biāo):在費(fèi)用最小的前提下,被感染的計(jì)算機(jī)的數(shù)量最少.研究計(jì)算機(jī)病毒模型是為了更好地控制計(jì)算機(jī)病毒的傳播,在此目的上,本文建立一個新的計(jì)算機(jī)病毒最優(yōu)控制模型,通過有效的控制策略,成功地將感染病毒的節(jié)點(diǎn)控制在一個較低的水平,利用數(shù)值模擬進(jìn)一步揭示了使用適當(dāng)?shù)目刂品椒ㄖ?能夠有效控制計(jì)算機(jī)病毒的傳播,并且在有控制的條件下得到的效果比沒有控制的條件下的模型的效果好,這也說明研究帶有控制的計(jì)算機(jī)病毒模型更具有實(shí)際意義.

1PachputeG,ChakrabartySP.DynamicsofhepatitisCunderoptimaltherapyandsamplingbasedanalysis. Communications in Nonlinear Science and Numerical Simulation, 2013,18(8):2202～2212

2MouofoPT,TewabJJ,MewoliB,BowongS.Optimalcontrolofadelayedsystemsubjecttomixedcontrol-stateconstraintswithapplicationtoawithin-hostmodelofhepatitisvirusB. Annual Reviews in Control, 2013,37(2):246～2593CostanzaV,RivadeneiraPS,BiaforeFL.OptimizingthymicrecoveryinHIVpatientsthroughmultidrugtherapies. Biomedical Signal Processing and Control, 2013,8(8):90～974LashariAA,ZamanG.Optimalcontrolofavectorbornediseasewithhorizontaltransmission. Nonlinear Analysis: Real Word Applications, 2012,13(1):203～212

5BlaynehKW,CaoY,KwonHD.Optimalcontrolofvector-bmediseases:treatmentandprevention. Discrete and Continuous Dynamical Systems-Series B, 2009,11(3):587～611

6JungIH,KangYH,ZamanG.OptimaltreatmentofanSIRepidemicmodelwithtimedelay. Biosystems, 2009,98(1):43～50

7MishraBK,JhaN.Fixedperiodoftemporaryimmunityafterrunofanti-malicioussoftwareoncomputernodes. Applied Mathematics and Computation,2007,190(2):1207～12128YangLX,YangXF.Thespreadofcomputervirusesundertheinfluenceofremovablestoragedevices. Applied Mathematics and Computation, 2012,219(8):3914～3922

9FengLP,HanQ,WangHB,etal.EffectiveimmunemeasuresonP2Pbotnets. Journal of Computer Application, 2012,32(9):2617～2619,2623

10BillingsL,SpearsWM,SchwartzIB.Aunifiedpredictionofcomputervirusspreadinconnectednetworks. Physics Letters A, 2002,297(6):261～266

11MishraBK,SainiD.Mathematicalmodelsoncomputerviruses. International Journal of Applied Mathematics and Computer Science, 2007,187(2):929～936

12YangLX,YangXF,ZhuQY,etal.Acomputervirusmodelwithgradedcurerates. Nonlinear Analysis: Real World Applications, 2013,14(1):414～422

13陳方方,洪靈.一類具有時滯和非線性發(fā)生率的SIRS傳染病模型穩(wěn)定性與Hopf分岔分析.動力學(xué)與控制學(xué)報(bào),2014,12(1):79～85 (ChenFF,HongL.StabilityandhopfbifurcationanalysisofadelayedSIRSepidemicmodelwithnonlinearsaturationincidence. Journal of Dynamics and Control, 2014,12(1):79～85 (inChinese))14MisraAK,VermaM,SharmaA.Capturingtheinterplaybetweenmalwareandanti-malwareinacomputernetwork. Applied Mathematics and Computation, 2014,229:340～349

15KamienMI,SchwartzNL.Dynamicsoptimization:thecalculusofvariationsandoptimalcontrolineconomicsandmanagement.Netherland:ElseverScience, 2000

16QiXH,HuangJQ,DongHR,YangZJ.Moderncontroltheoryandapplications.Beijing:NationalDefenceIndustryPress, 2007:186～191

17張旭龍,楊小帆.計(jì)算機(jī)病毒的最優(yōu)控制模型.計(jì)算機(jī)應(yīng)用研究,2011,28(8):3040～3043 (ZhangXL,YangXF.Optimalcontrolforcomputerviruses. Applied Research of Computers, 2011,28(8):3040～3043 (inChinese))

*Researchon3DreservoirdataprocessingbasedonArtificialIntelligence

?CorrespondingauthorE-mail:13240766843@163.com

29July2014,revised19May2015.

ANOPTIMALCONTROLMODELFORANEWTYPEOFCOMPUTERVIRUS?

ZhaoFuqun?

(Xianyang Normal University, College of Education Science, Xianyang712000, China)

Duetotheexistenceofcomputervirus,largenumbersofcomputerscannotrunnormally.Itusuallyresultsinhugeloss.Tothisend,ancontrolmodelforanewtypeofcomputervirusbasedonageneralcomputervirusmodelisproposedinthispaper.Firstly,anewtypeofcomputervirusmodelisimproved,andthecontrolistakenintoaccount.Theoptimalcontrolproblemisthenproposed.Meanwhile,theexistenceofoptimalcontrolisproved.Pontryagin’sminimalprincipalisemployedtoanalyzetheoptimalcontrol.Finally,thetheoryanalysisisalsosupplementedasacomparisonwork.Thesimulatingresultsshowsthatundertheconditionwithoutcontrol,thebasicreproductivenumberisobtainedfromtheoriginalmodel,anditisbiggerthan1.Moreover,aboveconclusionindicatesthatthereexiststheendemicequilibrium,anditleadstotheoutbreakofthecomputervirusfinally.Thenumericalmodelingshowsthatthroughtheoptimalcontrolstrategy,thespreadofcomputerviruscanbepreventedeffectively.

computervirus,minimumprincipal,optimalcontrol,numericalsimulation

E-mail:13240766843@163.com

10.6052/1672-6553-2015-036

2014-07-29收到第1稿,2015-05-19收到修改稿.

*基于人工智能的三維油藏?cái)?shù)據(jù)處理研究(07XSYK224)