Growth of Solutions of Higher Order Complex Linear DifferentialEquations in an Angular Domain of Unit Disc
Jianren Long
1School of Mathematics and Computer Science,Guizhou Normal University,Guiyang 550001,Guizhou Province,P.R.China.
2School of Mathematical Sciences,Xiamen University,Xiamen 361005,Fujian Province,P.R.China.
Growth of Solutions of Higher Order Complex Linear DifferentialEquations in an Angular Domain of Unit Disc
Jianren Long1,2?
1School of Mathematics and Computer Science,Guizhou Normal University,Guiyang 550001,Guizhou Province,P.R.China.
2School of Mathematical Sciences,Xiamen University,Xiamen 361005,Fujian Province,P.R.China.
.We study the growth of solutions of higher order complex differential equations in an angular domain of the unit disc instead of the whole unit disc.Some conditions on coefficient functions,which will guarantee all non-trivial solutions of the higher order differential equations have fast growing,are found in this paper.
AMS(2010)Mathematics Subject Classification:34M10,30D35
Complex differential equation,analytic function,iteratedn-order,angular domain,unit disc.
1 Introduction and main results
For a functionfmeromorphic in the unit disc?={z:|z|<1},the order of growth is given by
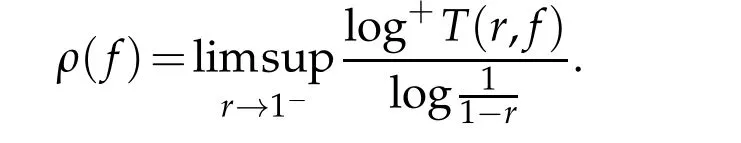
Iffis an analytic function in?,then the order of growth offis often given by
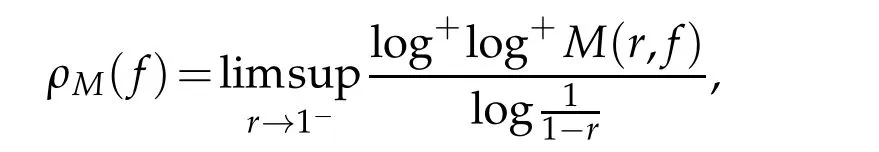
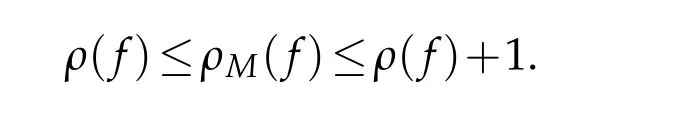
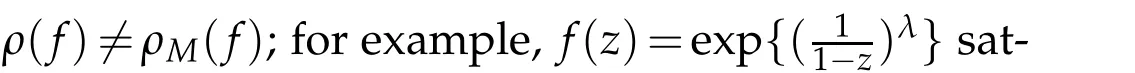
For the function of fast growth in?,we also need the definition of iteratedn?order,which can be found in[3].It is defined by
for any analytic functions in?.However,it follows from Proposition 2.2.2 in[14]thatρn(f)=ρM,n(f)forn≥2.In general,ρ2(f)orρM,2(f)are called hyper-order offin ?.In this paper,we assume that the reader is familiar with the fundamental results and standard notation of the Nevanlinna’s theory of meromorphic functions in ?,see[13]and[21]for more details.
The meromorphic functions in?can be divided into the following three cases:
(1)Bounded type:T(r,f)=O(1)asr→1?;
(3)Admissible in?:
It is always interested in studying the growth of solutions of linear differential equations in the unit disc by using the Nevanlinna’s theory of meromorphic functions.The analysis of slowly growing solutions has been studied in[5,8,9,11,12,15].Fast growth of solutions are considered in[1,3,4,8,10].There are a few results in studying the growth of solutions of differential equations in an angular domain.One of our main purpose of this paper is to investigate the properties in an angular domain of solutions of linear differential equation of the form
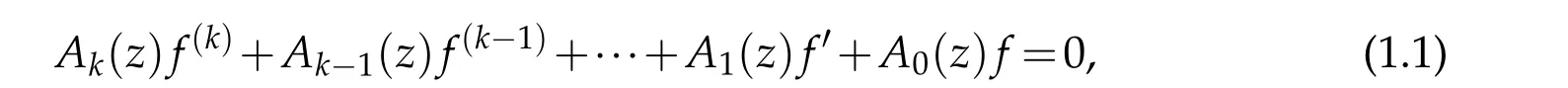
In[8],Heittokangas studied the growth of solutions of second orderlinear differential equations and obtained the following result.
Theorem 1.1.([8])Suppose that A0(z),A1(z)are analytic functions in?satisfying one of the following conditions.
(1)ρ(A1)<ρ(A0);
(2)A0(z)is admissible while A1(z)is non-admissible.
Then all non-trivial solutions of the equation

are of infinite order.
In[4],Chen generalized Theorem 1.1 to consider arbitrary order equation(1.1).The result is stated as follows.
Theorem 1.2.([4])Suppose that A0(z),A1(z),...,Ak(z)are analytic functions in?satisfying
one of the following conditions.
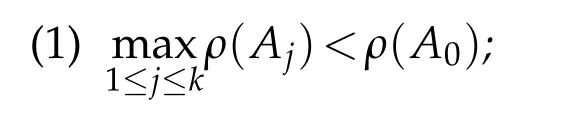
(2)Aj(z)is non-admissible while A0is admissible,where j=1,...,k.
Then all non-trivial solutions of the equation(1.1)are of infinite order.
In[20],Wu studied the growth of solutions of the equation(1.2)in an angular domain by using the Nevanlinna’theory in an angular domain(see[7,Chapters 1 and 3]),and obtained the following result.
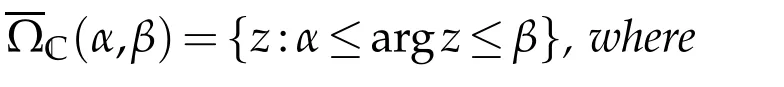
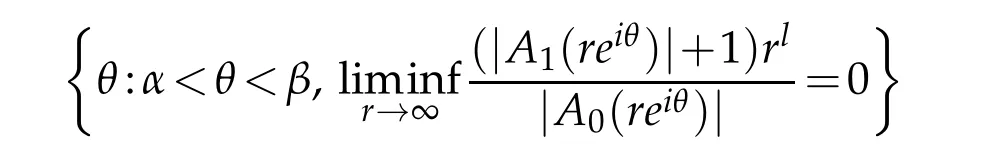
is greater than zero,then any non-trivial solutions f of(1.2)satisfies ρα,β(f)=∞.
Remark 1.1.The orderρα,βin Theorem 1.3 is defined by
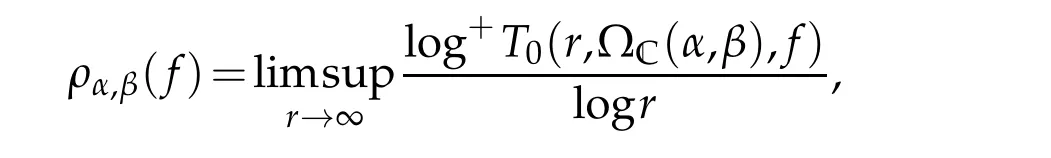
whereT0(r,?C(α,β),f)is Ahlfors-Shimizu characteristic in the angulardomain ?C(α,β)={z:α<argz<β},see[7]for more details.
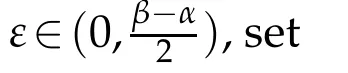
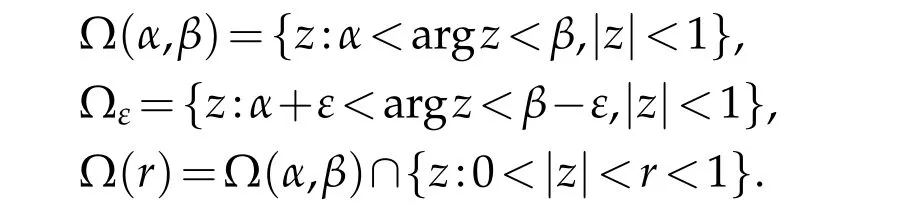
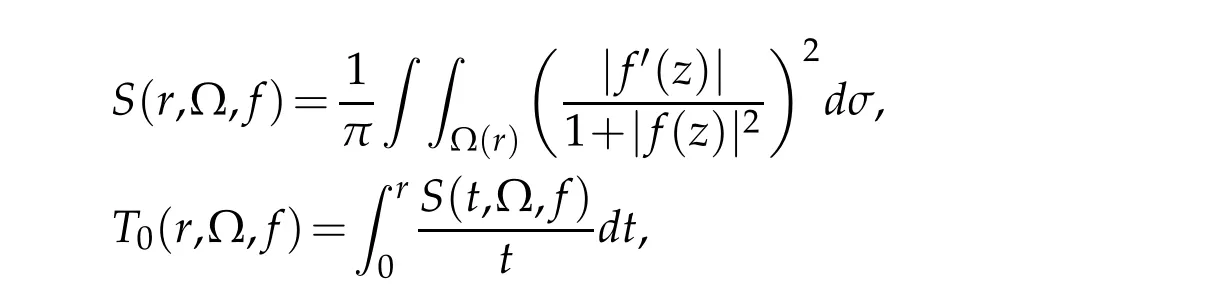
wheredσ=rdrdθforz=reiθ.
The order of growth of a meromorphic functionfin ? is defined by
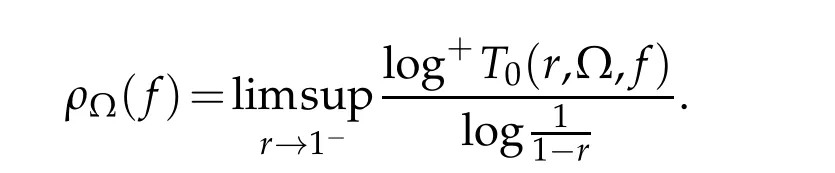
For fast growing of meromorphic functions in ?,we use the iteratedn-order to measure its growing,which is defined by
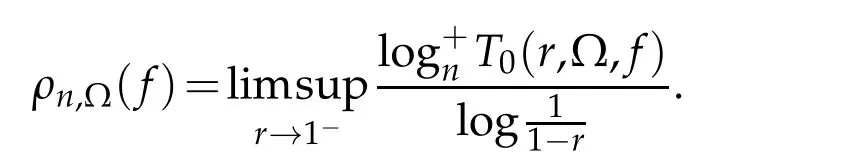
We remark that the definitions ofρ?(f)andρn,?(f)of a meromorphic functionfin ?are reasonable,because
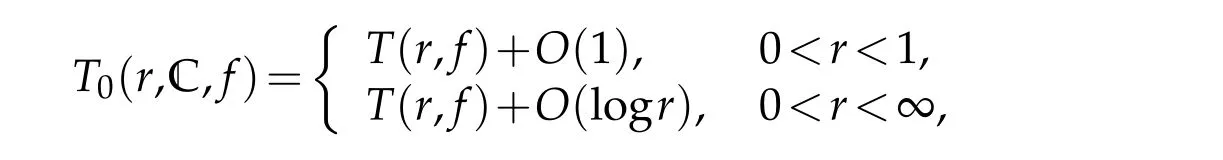
where C denotes whole complex plane.
Similarly the case of unit disc,for the meromorphic functionsfin ?,we also divide into the following three classes:
(1)Bounded type:T0(r,?,f)=O(1)asr→1?;
(3)Admissible in ?:
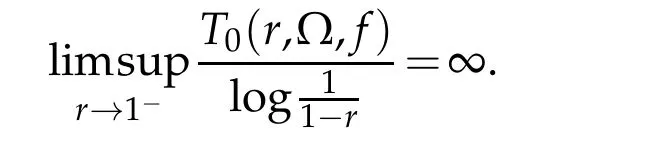
In this paper,we mainly obtain the following results by using the similar way of[19].
Theorem 1.4.Let A0(z),A1(z),...,Ak(z)be analytic functions in?={z:α<argz<β,|z|<1}.
If
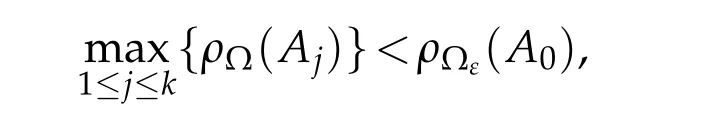
then every non-trivial solution f of(1.1)satisfies
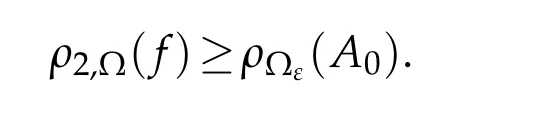
To state the second result,we also need the following notations.ForH?[0,1),the upper and lower densities ofHare given,which can be found in[3],by
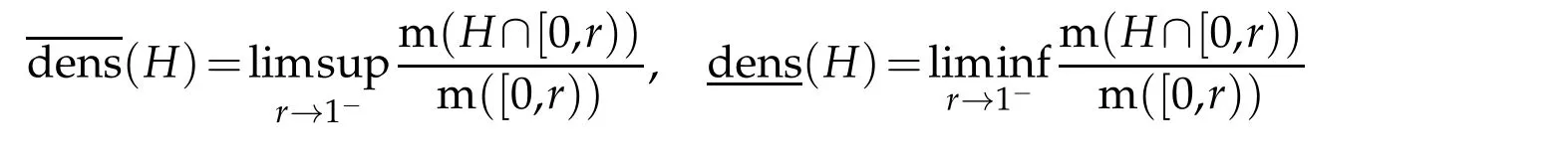
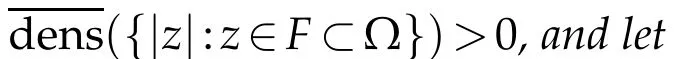
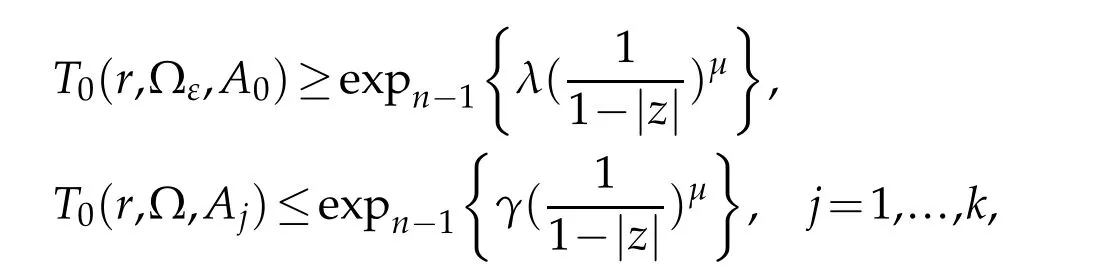
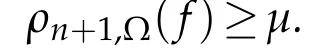
2 Auxiliary results
In this section,we give some auxiliary results for the proof of our theorems.The proof of the following lemma can be found in[16]plays an important role in proving our results.
Lemma 2.1.Let
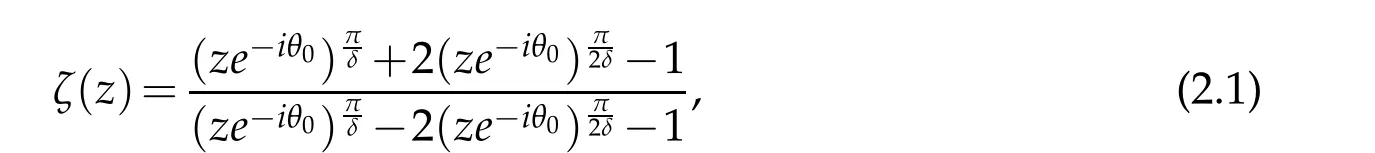
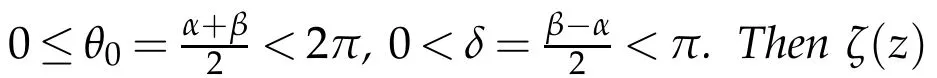
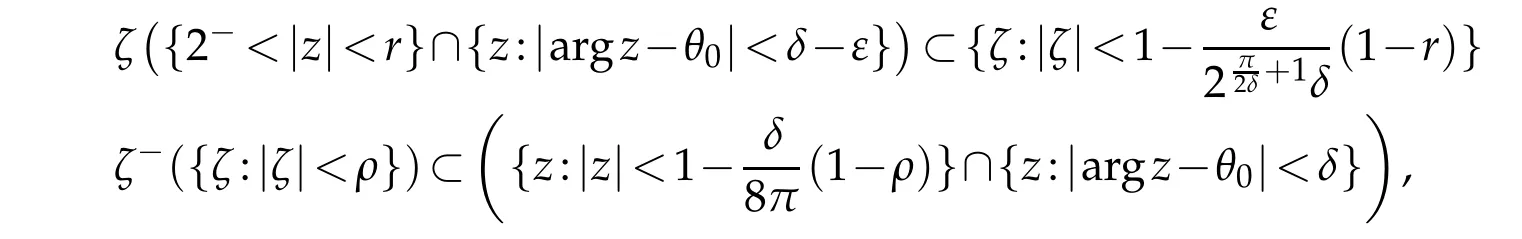
where ρ<1is a constant.The inverse transformation of(2.1)is
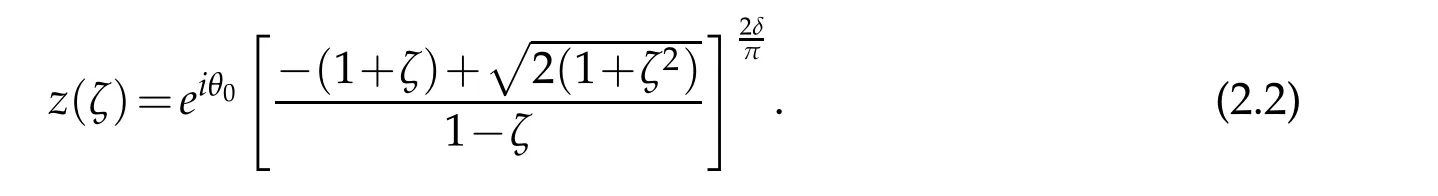
The following lemma due to Wu[19].
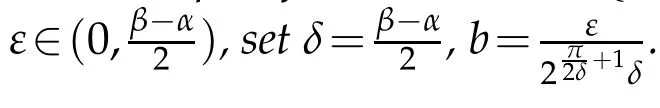
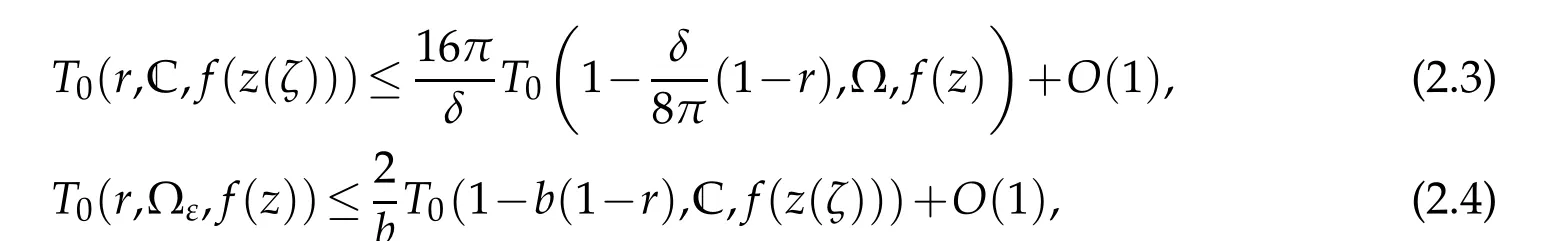
where z(ζ)is the inverse transformation of(2.1).
Remark 2.1.Applying the formulaT(r,f)=T0(r,C,f)+O(1),Lemma 2.2 and the definition of iteratedn-order,we immediately obtain that
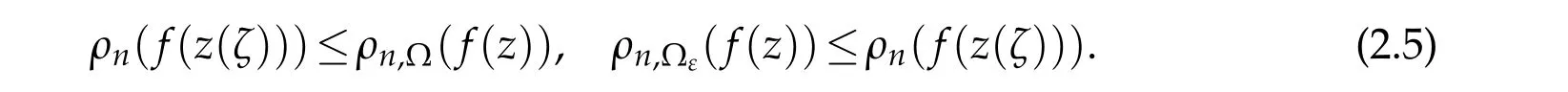
The following lemma can be proved by the same method of[6,Lemma 1],see also[19,Lemma 2.3].
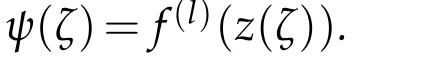
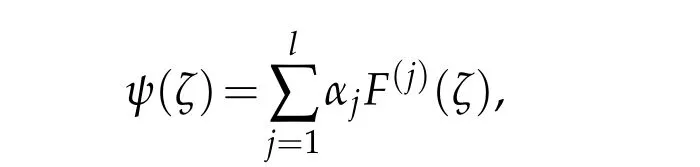
3 Proofs of theorems
Proof of Theorem 1.4.Suppose thatfis a non-trivial solution of(1.1)in ?.Applying
Lemma 2.3,we have
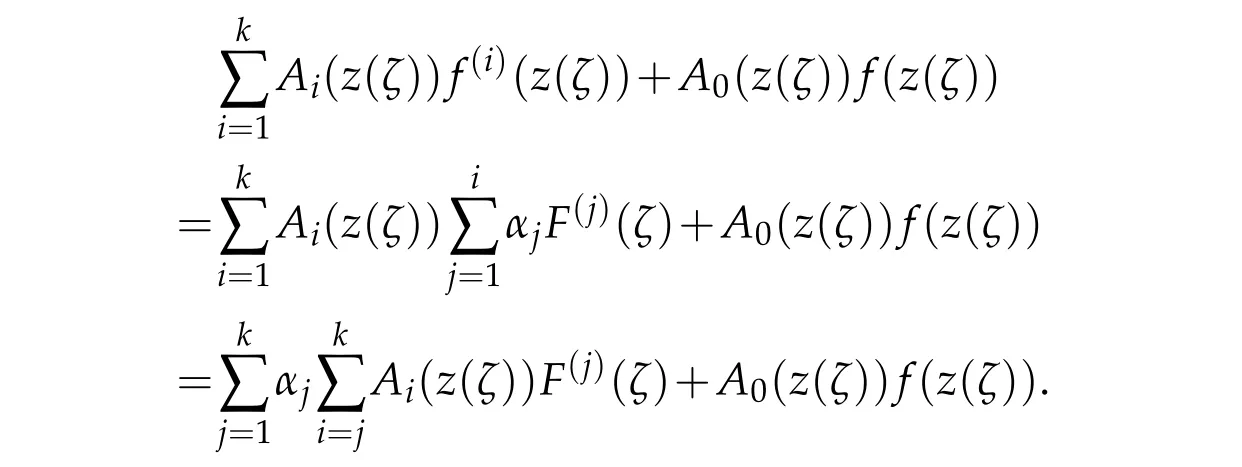
ThenF(ζ)=f(z(ζ))is a solution of the differential equation
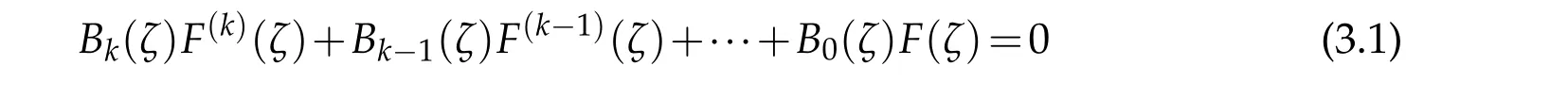
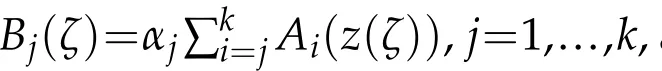
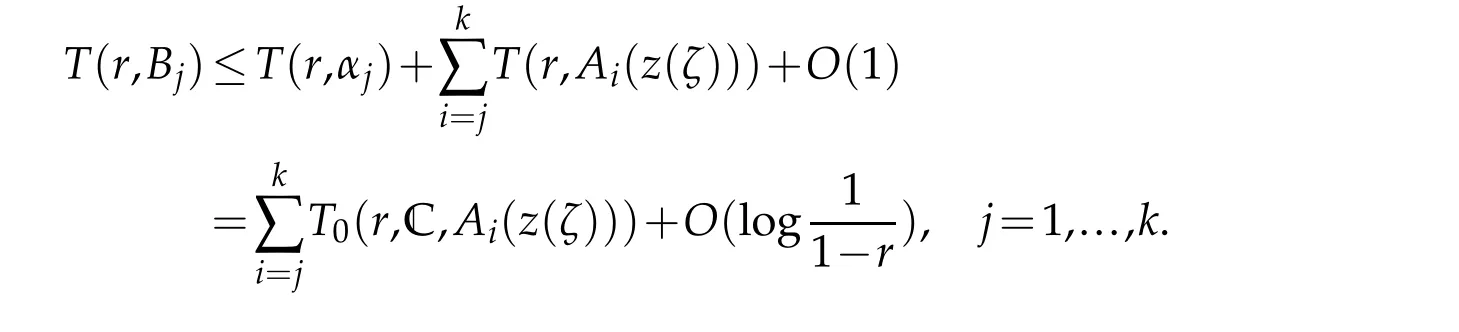
Applying Lemma 2.2 and our conditions,we get
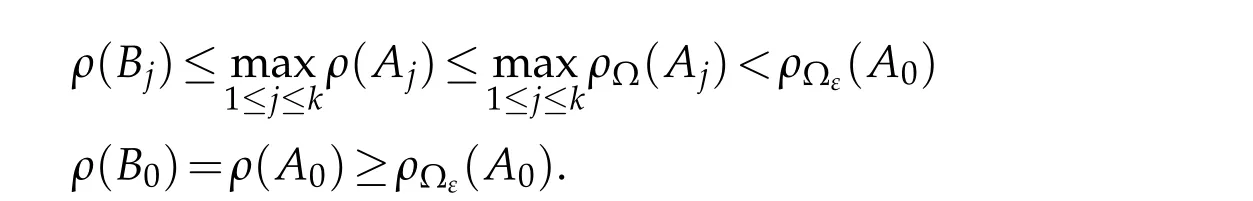
It follows from two inequalities above that

By[2,Theorem 2.2],we getρ2(F)≥ρ(B0)for all non-trivial solutionsFof(3.1).It follows from this and(2.5)that
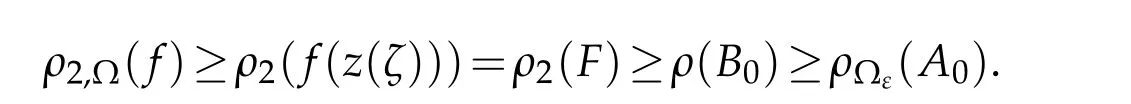
Thusρ2,?(f)≥ρ?ε(A0)for all non-trivial solutions of(1.1).This completes the proof.
Proof of Theorem 1.5.Suppose thatfis a non-trivial solution of(1.1)in ?.By using the similar reasoning ofthe proofofTheorem 1.4,we get(3.1).By(2.3)and(2.4)in Lemma 2.2,we get
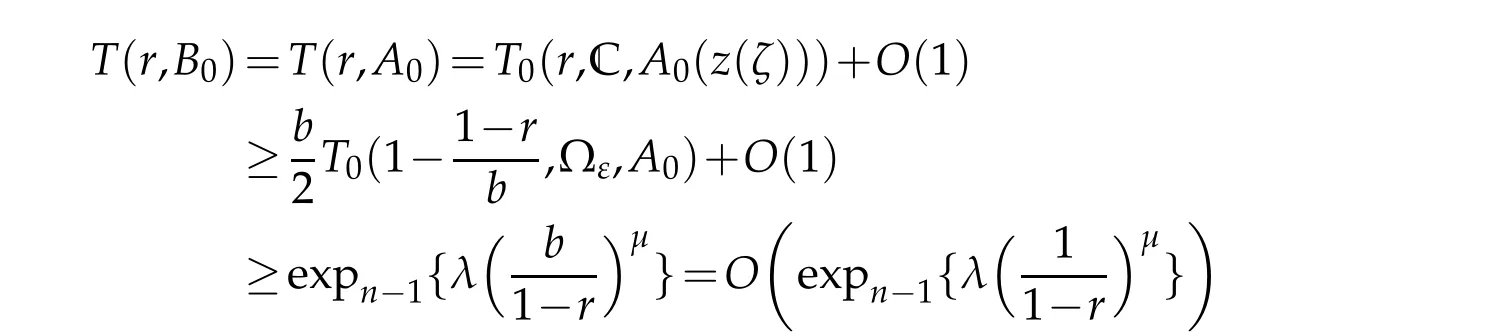
and forj=1,...,k,
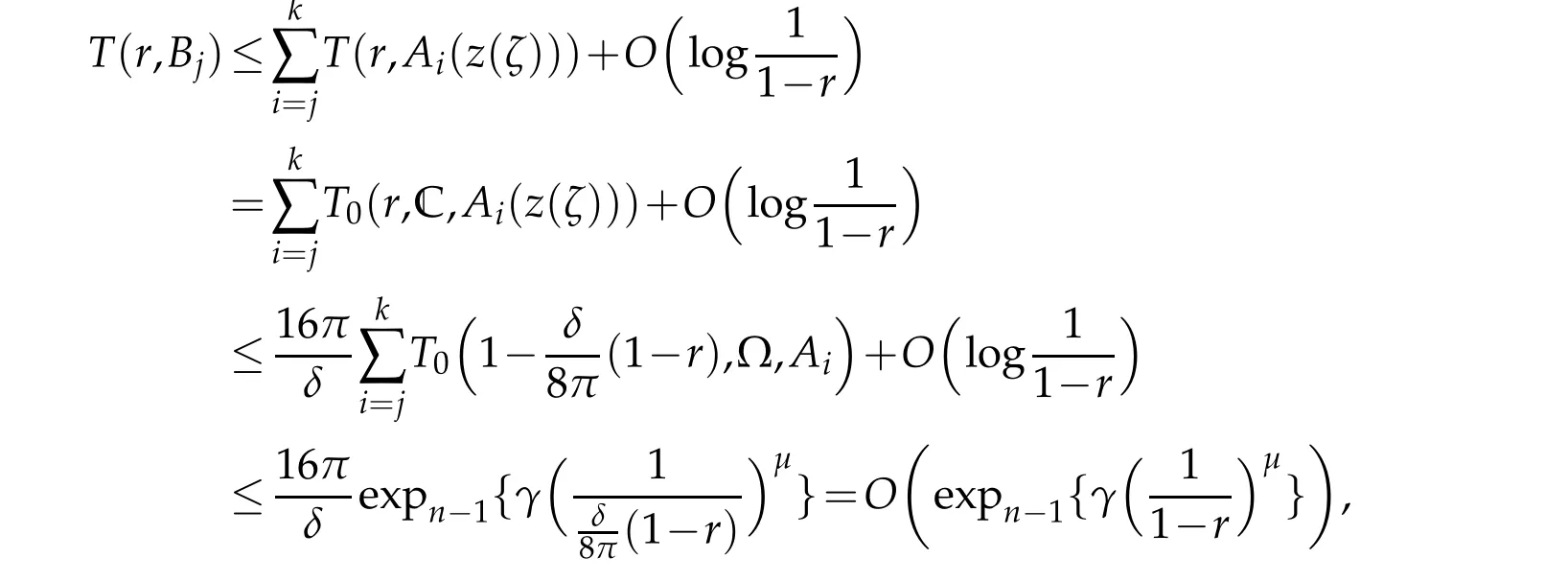
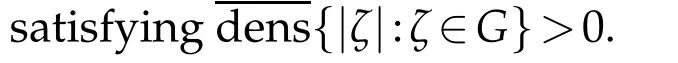
Applying[3,Theorem 1.3],we getρn(F)=∞ andρn+1(F)≥μfor all non-trivial solutionsFof(3.1).It follows from this and(2.5)that
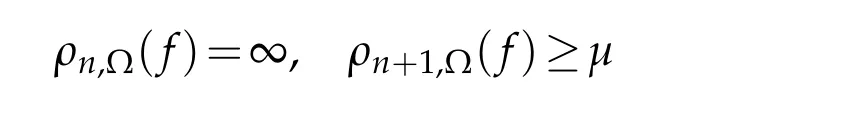
for all non-trivial solutionsfof(1.1).This completes the proof.
Acknowledgments
The author would like to thank the anonymous referees for the valuable comments and suggestions in improving this paper.This research is supported in part by the Foundation of Science and Technology of Guizhou Province(Grant No.[2015]2112),and the National Natural Science Foundation of China(Grant No.11171277,11501142,11571288).
[1]D.Benbourenane and L.R.Sons.On global solutions of complex differential equations in the unit disc.Complex Var.Elliptic Equa.,49:913-925,2004.
[2]T.B.Cao.On the complex oscillation theory of linear differential equations with analytic coefficients in the unit disc.Acta Math.Sci.,28A(6):1046-1057,2008,(In Chinese).
[3]T.B.Cao.The growth,oscillation and fixed points of solutions of complex linear differential equations in the unit disc.J.Math.Anal.Appl.,352:739-748,2009.
[4]Z.X.Chen.The properties of solutions of a class of differential equations in the unit disc.J.Jiangxi Norm.Univer.,26(3):189-190,2002,(In Chinese).
[5]Z.X.Chen and K.H.Shon.The growth of solutions ofdifferentialequations with coefficients of small growth in the disc.J.Math.Anal.Appl.,297:285-304,2004.
[6]A.Edrei.Meromorphic functions with three radially distributed values.Trans.Amer.Math.Soc.,78:276-293,1955.
[7]A.A.Gol’dberg and I.V.Ostrovshii.Value Distribution of Meromorphic Functions,Translations of Mathematical Monographs.American Mathematical Society,Providence,RI,236,2008.
[8]J.Heittokangas.On complex differential equations in the unit disc.Ann.Acad.Sci.Fenn.Math.Diss.,122:1-54,2000.
[9]J.Heittokangas.Blaschke-oscillatory equations of the formf′+A(z)f=0.J.Math.Anal.Appl.,318:120-133,2006.
[10]J.Heittokangas,R.Korhonen and J.R¨atty¨a.Fast growing solutions of linear differential equations in the unit disc.Results Math.,49:265-278,2006.
[11]J.Heittokangas,R.Korhonen and J.R¨atty¨a.Linear differential equations with coefficients in weighted Bergman and Hardy spaces.Trans.Amer.Math.Soc.,360(2):1035-1055,2007.
[12]J.Heittokangas,R.Korhonen and J.R¨atty¨a.Linear differential equations with solutions in the Dirichlet type subspace of Hardy spaces.Nagoya Math.J.,187:91-113,2007.
[13]W.K.Hayman.Meromorphic Functions.Clarendon Press,Oxford,1964.
[14]I.Laine.Nevanlinna Theory and Complex Differential Equations.Walter de Gruyter,Berlin,New York,1993.
[15]C.Pommenrenke.On the mean grwoth of solutions of complex linear differential equations in the disk.Complex Var.Elliptic Equa.,1(1):23-38,1982.
[16]D.C.Sun and J.R.Yu.On the distribution of random Dirichlet series(II).Chin.Ann.Math.,11B:33-44,1990.
[17]M.Tsuji.Potential Theory in Modern Function Theory.Chelsea,New York,1975,reprint of the 1959 edition.
[18]J.F.Xu and H.X.Yi.Solutions of higher order linear differentialequations in an angle.Appl.Math.Letter,22(4):484-489,2009.
[19]N.Wu.On the growth order of solutions of linear differential equations in a sector of the unit disk.Results Math.,65:57-66,2014.
[20]S.J.Wu.On the growth of solutions of second order linear differentialequations in an angle.Complex Var.,24:241-248,1994.
[21]G.H.Zhang.Theory of Entire and Meromorphic Functions-Deficient and Asymptotic values and Singular Directions.Springer-Verlag,Berlin,1993.
14 April,2015;Accepted 10 July,2015
?Corresponding author.Email address:longjianren2004@163.com(J.R.Long)
 Journal of Mathematical Study2015年3期
Journal of Mathematical Study2015年3期
- Journal of Mathematical Study的其它文章
- Elliptic Systems with a Partially Sublinear LocalTerm
- Second Order Estimates for Non-concave Hessian Type Elliptic Equations on Riemannian Manifolds
- The Distortion Theorems for Harmonic Mappings with Negative Coefficient Analytic Parts
- Weak Convergence Theorems for Mixed Type Asymptotically Nonexpansive Mappings
- Global Strong Solution to the 3D Incompressible Navierv-Stokes Equations with General Initial Data
- Non-Isotropic Jacobi Spectral and Pseudospectral Methods in Three Dimensions
