ZHU Liang(朱亮),PU Peng(蒲鵬),DU Sha(杜莎),and HAN Ding-Ding(韓定定),

1School of Information Science and Technology,East China Normal University,Shanghai 200241,China

2Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Shanghai 201800,China

Simulation of neutron diffusion and transient analysis of MSR?

ZHU Liang(朱亮),1,2PU Peng(蒲鵬),1DU Sha(杜莎),1and HAN Ding-Ding(韓定定)1,?

1School of Information Science and Technology,East China Normal University,Shanghai 200241,China

2Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Shanghai 201800,China

Molten salt reactor(MSR)is a potential nuclear power reactor of Generation IV.The working process of the primary loop of an MSR is studied in this paper.A physical model is established to describe the coupled heat transfer for the MSR core channels,the temperature negative feedback and the neutron characteristics. The simulation code,NDP1D,has been developed with the object-oriented method,conducting the neutron diffusion and transient analysis in a parallel way.The simulation data and diagrams of neutron,power,f l ow rate and temperature can be obtained via graphical user interface.The simulation results can be used for further study on MSRs of larger dimensions and more complicated geometry.

Molten salt reactor,Neutron diffusion,Transient analysis,Simulation software

I.INTRODUCTION

The Generation IV International Forum(GIF)on nuclear energy aims at developing technologies to achieve safety performance,waste reduction and increased proliferation resistance,and to provide a nuclear energy option that is economically competitive[1].Of the six future nuclear power plants under the framework of GIF,only the Molten Salt Reactor(MSR)is of the liquid fuel type.The concept of MSR was initially proposed by Oak Ridge National Laboratory(ORNL)[2,3]where the feasibility was proved by both theories and experiments.In 2011,Chinese Academy of Sciences launched the project of Thorium Molten Salt Reactor Nuclear Energy System(TMSR).As part of the prestudy project,the molten salt reactor transient analysis considers key parameters(the power, fl ow rate,temperature and the controlling orders)and the physical properties of the core ( fl ow rate of the initial zero-power and low-power mode,temperature and the primary loop pressure).The transient analysis software also judges status of the reactor via different parameters.Therefore,the simulation methods are of much concern.

Current researches on MSR mainly focus on fi nding different descriptive approaches of the reaction procedures. Lapentaet al.[4]analyzed neutronics in a fl uid fuel system through a point-kinetics model.Dullaet al.[5,6]used the quasi-static method,which considered a prescribed velocity fi eld in one direction without taking the temperature crosssection feedback into account.Yamamotoet al.[7,8]and Suzukiet al.[9]analyzed the steady-state and transient state for a small molten salt reactor by coupling the neutron diffusion equations with the heat transfer in fuel salt and graphite. Krepelet al.used the DYN1D–MSR[10]and DYN3D–MSR[11]codes for solving the two-group neutron diffusion equation with a point kinetics model,and models of delayedneutrons drift and heat release distribution were included. The prompt f i ssion neutron source was calculated by means of the same nodal f l ux expansion method.Part of the neutrons was released with a time delay when the precursor core drifted with the liquid fuel along axial direction.An extended delayed neutrons model was developed.Transient simulating of 3D neutronics and parallel channel thermal hydraulics were used.

Lecarpentieret al.[12]developed the Cinsf1D program, which replaced MSRE at Oak Ridge to become the European benchmark of the transient simulation,and to study the AMSTERsystem[13].Bothsteady-stateandtransientstatecould besimulatedbytheCinsf1Dprogram.Aftermodelingthesalt fuel and the graphite in the reactor,the axial and radial power distribution of the core were calculated by the DRAGON program[14].Based on the diffusion theory with two energy groups,the neutron f l ux and the distribution of delayed neutron precursors were described in neutronics according to the cross sections.The thermal negative feedback depending on the cross sections was related to the temperatures of various mediums.Thermo hydraulics could be described by the energy balance between the salt fuel and graphite.A simplif i ed geometric model represented the typical core channel in the molten salt reactor.Also,a point kinetic model was included, where graphite temperature was a single average value,and the relationship between the temperature of the molten salt and the height of the core was linear.

In this paper,we report our work on simulating neutron diffusion and transient analysis in an MSR.Optimization of the model based on Cinsf1D will be discussed in Sec.II, with a focus on the transient analysis,which is separated from the point kinetic model.The implementation of objectoriented programming is discussed in Sec.III.The software architecture is improved to meet the standards of softwareengineering,high-performance computing and management viagraphicaluserinterface,andtoacquirethesimulationdata and diagrams in visualized forms.The results are shown in Sec.IV.In Sec.V,we conclude that the neutron diffusion and transient analysis of the MSR are simulated in a precise and eff i cient way.

II.THEORETICAL MODEL OF THE MSR PROCESS

A vertical-section diagram of the primary loop is shown in Fig.1.The molten reactor core consists of graphite re fl ector.The molten salt fuel contains beryllium fl uoride,lithium fl uoride,zirconium fl uoride,and uranium or thorium fl uoride.With the fi ssile materials and convertible molten salt at 600°C,the molten salt fuel exits from the core.The fuel salt fl ows sequentially from the left of the core to Pipe 1,next to the heat exchanger,then to Pipe 2,and fi nally back to the core.The molten salt reactor core is a cylindrical cavity with 199 parallel hexagonal graphite elements,each of which has a circular coolant channel.Each channel has a fuel passage in the middle.The calculation of the reactor core is divided into three zones,withh1,h2,andh3describing the length of each zone,rgbeing the channel diameter andrfbeing the inner diameter.The liquid salt serves as both the coolant and fuel. The graphite moderator in the reactor is heated by the neutrons and gamma rays produced in the fi ssion reaction process.The heat between the graphite moderator and coolant is exchanged through the heat exchanger.Controlling of the reaction is modeled as follows.

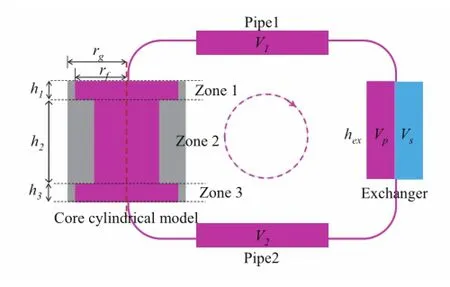
Fig.1.(Color online)The vertical-sectional diagram of the primary loop:the fuel salt f l ows as the dashed-circle is indicated.

A.Neutron Diffusion Modeling

In the neutron diffusion modeling,the neutrons are of two energy groups(the fast and thermal neutron energy groups) and one spatial dimension(z).The neutron energy groups are cut at 1.8eV.The f l ux of the molten salt reactor is calculated by the thermal spectrum.It has been shown that the axial direction(z)and radial direction(x)are relatively decoupled. The main object of the model is to compare the inf l uence of liquidity for the delayed neutron precursors,which are produced only in the core,drifted along axial(z)with the MSR core movement.The life spans of these neutrons are much shorter than the molten salt fuel cycle,so the neutrons are not affected by the velocity f i eld[15,16].

The neutron and precursors dynamics equations in the fuel material of molten salt reactor are derived from the particle conservation equations as follows:

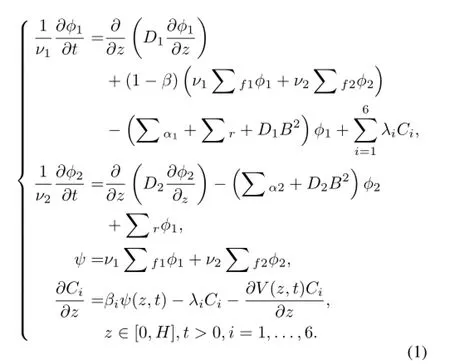
where,iis the delayed neutron group number.Vj=1,2indicates the neutron speed of groupj,withj=1 being the fast neutron energy group andj=2 the thermal neutron energy group.φj(z,t)is the neutron fl ux of groupj,tis the time,Dj(z,t)is the diffusion coef fi cient of groupj.βjis the proportion of emitted heat from the delayed neutron of groupi,andβis the sum of allβj,(z)and(z)are the macroscopic neutron fi ssion cross-section and the macroscopic neutron absorption cross-section of the groupj,respectively;is the neutron diffusion cross-section from the fast neutron group towards the thermal group;B2is the radial leakage coef fi cient;λjis the delayed neutron decay constant of groupi;Cj(z,t)is the linear precursor concentration of groupi.ψ(z,t)is the number of neutrons emitted by fi ssion per unit height of the reactor;andV(z,t)is the moltensaltspeedvector.Duetothelongdecaytimeofthedelayedneutrons,theyaresupposedtodriftwiththemoltensalt, which means that the pioneer nuclear has the same speed with the molten salt without considering the interaction of them.

B.Thermal Negative Feedback

Thediffusioncross-sectioncanbewrittenasafunctionofzand temperature.Thus,according to the diffusion theory,the cross-section as a function ofzat a certain temperature can be calculated through the interpolation using standard crosssectiondata.Thus,Eq.(1)canbesolvedtoobtainthef l uxand power released.The reactivity is affected by temperature and balance conf i guration of salt and graphite,and the control rod depth,butpresetdatacanbepreparedtoevaluatethediffusion process simulation.

C.Thermal Hydraulics

The calculation is divided into two parts,the core and the heat exchanger,using lumped parameter model.

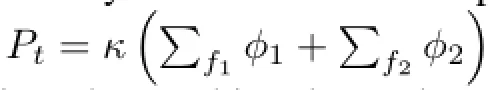
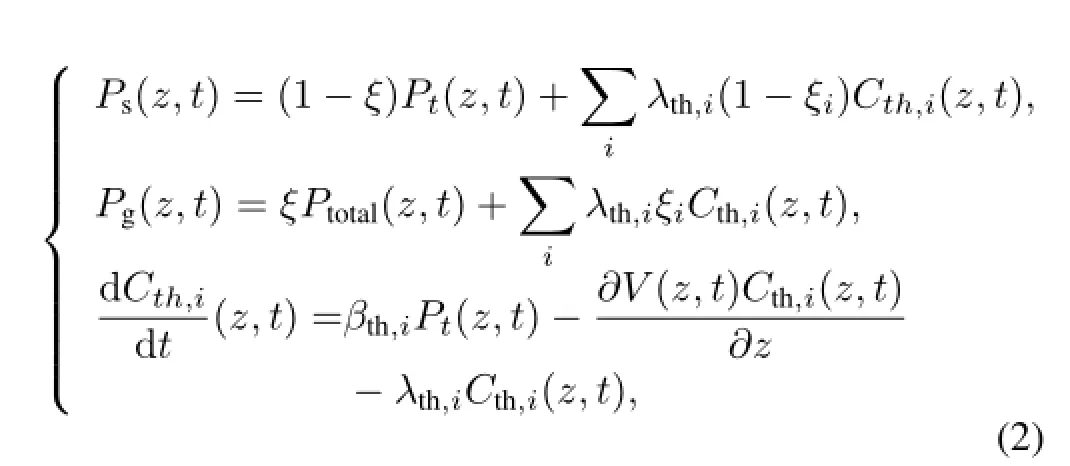
where,ξi=exp(?λiΔt);Cth,i(z,t)is the density per unit length for delayed precursors of groupi;andλ,βandVare of the similar def i nitions to those in Eq.(1).

The heat exchange between the salts in the primary and secondary loops is described by thermal convection equations,taking into account the heat emission due to the decrease of delayed thermal precursors.The f l ow rateDis related with volumeV,temperatureT,zand timetas:

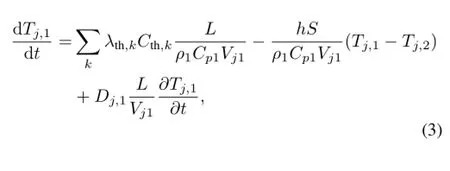
where footnote 1 stands for the primary loop and 2 for the secondaryloop.ρissaltdensity,andcpistheheatingcapacity at constant pressure,Sis the exchange surface,andhis a coef fi cient of exchange per unit surface area.The total salt fl ow in the primary loop is calculated byD(t)=1(t), (j=1→6).

Between the core outlet and the inlet of heat exchanger,the fuel salt passes a high-temperature zone without heat transfer, namely Pipe 1 in Fig.1;similarly,between the bottom outlet of the heat exchanger and the core inlet the fuel salt passes a low-temperature zone,namely Pipe 2.Therefore,the heat exchanger is calculated in three parts:above the heat exchanger, the heat exchanger and below the heat exchanger.Each of the parts is calculated on the assumption that temperatures of the boundary and precursor concentrations in all parts are continuous.

III.THE REALIZATION OF THE SIMULATION SOFTWARE

According to the physical model and the geometric model of the MSR,simulation code Neutron Diffusion Program for 1D(NDP1D)for one-dimensional neutron diffusion and transient analysis was f i nished with the following featuress:

?To analyze and design the structure of the coupled program of neutron diffusion and transient analysis.Based on physical function of the neutron diffusion process, design the data structure and f i le operations in a hierarchical and modular way;

?To achieve the function of each module and to complete optimization of the program algorithm and computational eff i ciency;

?To transplant the original code into an architecture suitable for parallelization;

?To reserve open programming interface for further improvements the transient analysis program on multigroup and complicated geometry.

NDP1D is written in C++,the object-oriented language, combinedwith thelinearalgebranumericallibrary ublas(part of the library Boost,launched by the C++Standards Committee Library Working Group members),shared memory parallel library OpenMP,as well as the cross-platform graphical user interface framework tools Qt.

A.Calculation Process of NDP1D

The NDP1D is divided into critical and transient calculations.Their f l ow charts are shown in Figs.2 and 3,respectively.

Thesaltfueltemperaturealongtheaxisziscalculated.The macroscopic cross-section is linearly interpolated to calculate the thermal characteristics of molten salt and the graphite by adjusting the radial leakage and the uranium concentration and by using the input table of reaction cross-section data.At a f i xed temperature,the neutron f l ux equations containing a concentration of delayed neutrons are resolved,and the f l ux is normalized by the core power.In transient calculations, the depth and speed of control rod is considered.Flow rate, coupled with heat exchange rate,is determined by the status of reactor.And the input table of reaction cross-section data is linearly interpolated to get the macroscopic cross-section at timet.

Then the neutron f l ux and delayed neutron precursors concentration at the next time step are calculated by the crosssection and f l ux at timet.By using the distribution of temperature and the power released in the time interval to calculate temperature of the core salt,temperatures of the graphite and heat exchanger are calculated at the next moment.Considering situations where some more vectors,matrix operations,fi le reading and writing operations are involved in the calculation and frequently repeated calls,a certain amount optimization and parallelization have been done to adapt the multidimensional data simulation.

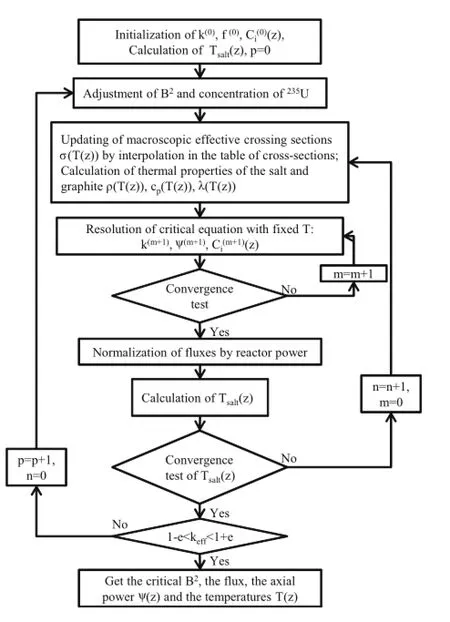
Fig.2.Flow chart for critical calculation.

B.Optimization of NDP1D

Based on the Cinsf1D code,the program is optimized in three aspects:functionality,syntax and data structures.

?The calculation of diffusion model has been separated according to functionality into several relatively independent modules,which can be tested separatly.Coupling of the program is reduced to improve the readability,being conducive to expansion and the second revision;

?With the unique pointer characteristics in C++,the data transfer procedure of the program is optimized to avoid the operations in Cinsf1D written in Fortran,which only supports transferring the real parameters instead of formal parameters;

?The stringstream object of C++is used in NDP1D to simplify the type and upgrade f i le reading and writing to the memory-level and object-level,hence the reading speed and security is greatly improved.

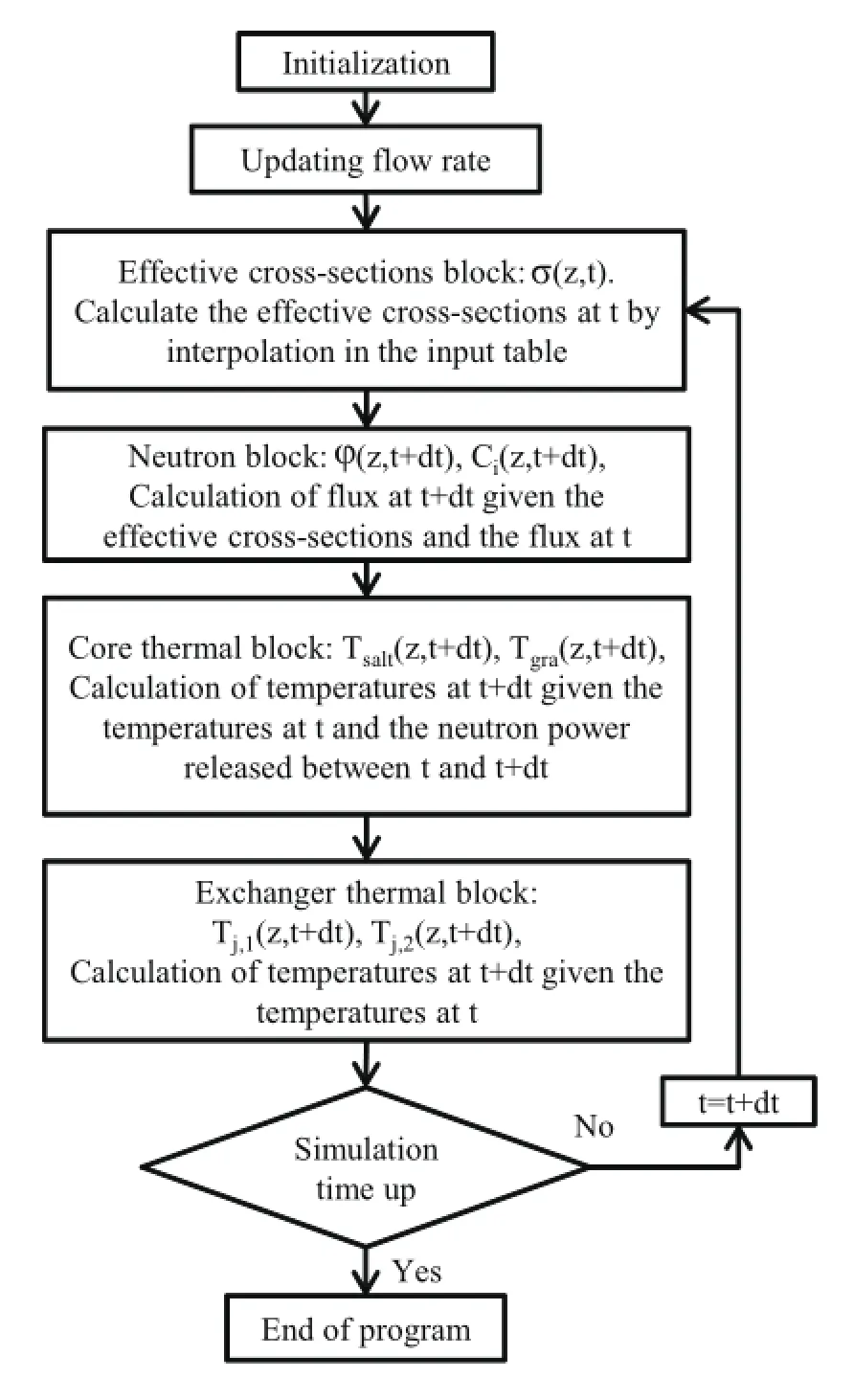
Fig.3.Flow chart for transient calculation.

C.Parallelization of NDP1D

For one-dimensional case,the code can be run on just a single computer or one node of a computing cluster,so it is parallelized using shared memory model,i.e.OpenMP.The parallel execution of the model is the Fork-Join.With time analysis,physical models and code analysis as well as the OpenMP parallelization,the performance of this program has been improved and CPU load can be equalized.

1.Parallel analysis of NDP1D

Combined with the above physical model,parameters of the model and calculation involved have been analyzed:

a.The mathematical equations resolution:MATHFONC ::SOLVETSYS,MATHFONC::SOLVES SYSTEM are respectively the LU decomposition and the main–element elimination method,solving the linear equations AX=Y.In both methods,the former can be paralleled in the process of back substitution;the latter can be in the elimination process of the primary line to other lines.Due to the usage of lower proportion of LU decomposition algorithm,smaller size of the one-dimensional program,and the larger cost of parallelization,we have considered the main-element elimination method to get effective parallelization.

TABLE 1.Upgraded FECs threshold consistency test

b.File reading and writing:the program inputs data from theneutron,thermo,transient,geometryandother fi les; for outputing codes,results are written to some data fi les.Since the reading and writing of fi les does not interfere with each other,the CPU can exchange data with the cache in parallel,and then read and write the hard disk to reduce the waiting time between peripherals.On the other hand, fi le reading and writing is in parallel with other calculations in order to effectively use the waiting time of reading and writing.

c.The main cycle in transient simulation:pipeline parallelism is a better choice concerned for continuous cycle of code.Because the loop of the transient simulation in main program contains a large number of interdependent variables which are in serial execution and each cycle is highly dependent on the calculation results of the last cycle,it is very diff i cult to parallelize and the model and algorithm modif i ed should be sought to accommodate parallelization.

2.Results of parallelization

The CPU time of the optimized code is 37.84s,whereas it was 51.32s before.In comparison,the speed-up ration isS≈1.36.Although it does not reach linear acceleration,p/log2p≤S≤p,yet it has been greatly improved.For current scale of the code,there are two trends for the parallelization results:when only a small amount of parallelization is implemented,the calculation speed gets higher,but CPU load is unbalanced,as shown in Table 1;when the parallelized part is greater,the calculation speed is not signif icantly increased,or even gets slower,but CPU load is more balanced.The reason is that the large serial part is unable to be parallelized.Also,the small code scale is of high cost of parallelization.A possible way to improve the application performance of the code is to increase the number of threads based on Amdahl’s law[19],or to increase workload according to Gustafson’s Law[20].Another way of parallelization using GPU[21],specif i cally CUDA[22],will also be considered in future work.

IV.THE SIMULATING RESULTS OF NDP1D

The graphical interface of NDP1D is written in Qt,a C++ cross-platform graphical user interface development framework,as shown in Fig.4.The diagrams displayed are generated by Root codes,which are integrated into NDP1D.

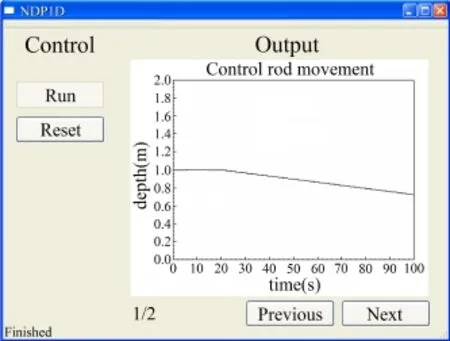
Fig.4.(Color online)User interface of NDP1D,showing the change of control rod depth.

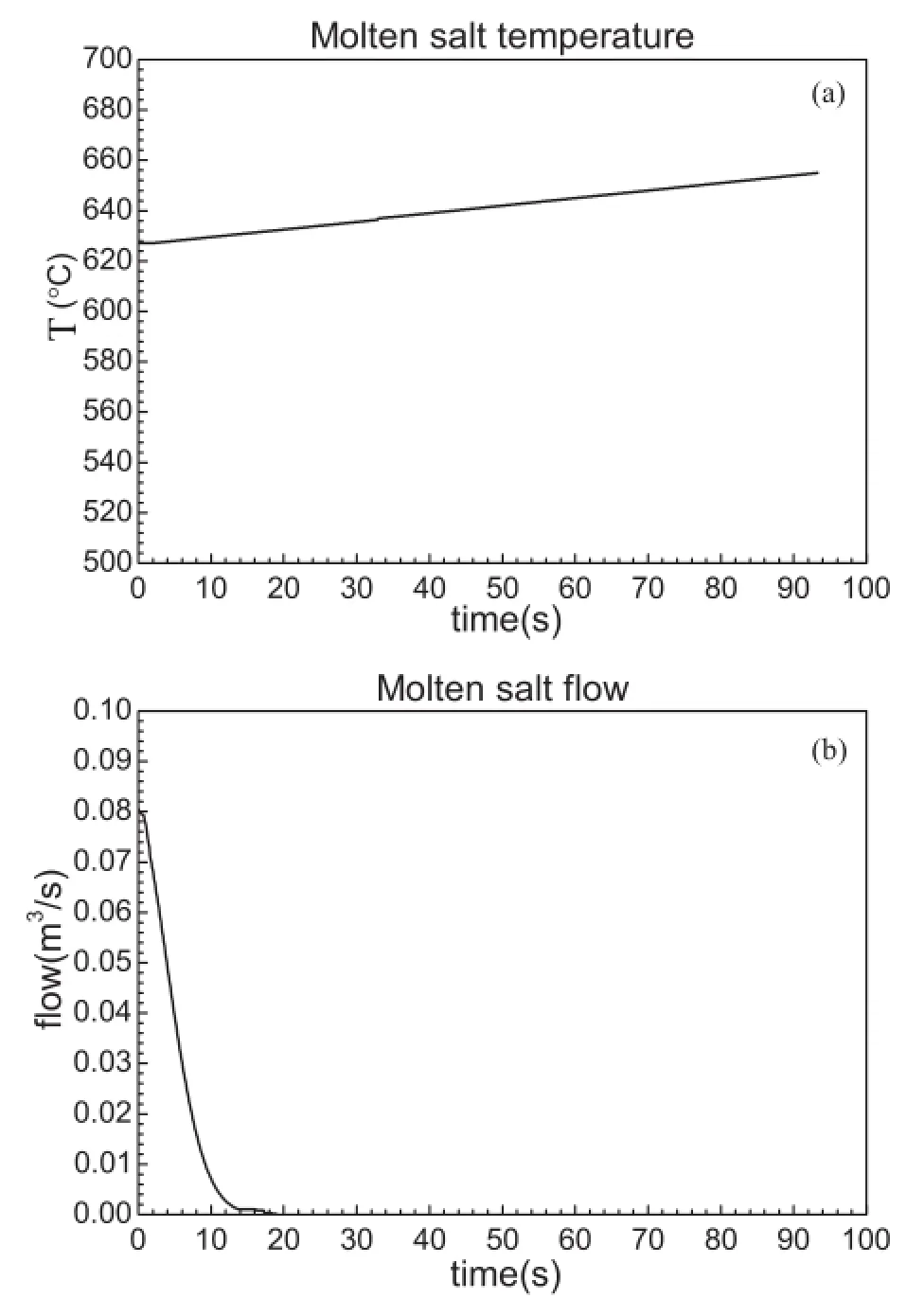
Fig.5.Constant power shutdown with(a)increasing temperature of molten salt and(b)rapid decrease of molten salt f l ow rate.

An important simulating process is reactor shutdown. When the reactor is shut down,the power of the reactor goes from the level of operation down to the neutron source level. For validation,a benchmark test,the shutdown of constant power,is performed,and the results are shown in Fig.5,with both the molten salt f l ow rate and temperature mainly tested. Also,the control rod depth is shown in Fig.4.The simulation results of NDP1D program consists with the calculation results of analytical method.

V.CONCLUSION

The simulation of neutron diffusion and transient analysis of the molten salt reactor has been discussed in this paper,which established an effective physical and geometric model and built a theoretical foundation for the development of the one-dimensional neutron diffusion and transient analysis calculation software NDP1D.The optimized program has reduced the degree of coupling among modules and the redundancy,in line with the software engineering.On the other hand,the program’s performance has been improved and the hardware load has been more balanced after parallelization. With the help of simulation software NDP1D,multiple results have been acquired,such as the simulation of constant power shutdown,including changes of molten salt f l ow rate,temperature and control rod depth.Although the software NDP1D we developed is just one-dimensional simulation,and some conditions are set close to the ideal states of transient analysis,the studying methods and framework of the software as well as the reactor physics and thermal coupling model can be the basis for follow-up projects to further explore transient analysis on molten salt reactors with higher dimension and more complicated geometry.

ACKNOWLEDGMENTS

The authors acknowledge the support from CAI Xiang-Zhou,GUO Wei,ZHAN Zhi-Chao,YU Ming-Xiang and SHI Hong-Li.

[1]DOE.A Technology Roadmap for Generation IV Nuclear Energy Systems.Issued by the US DOE,2003.

[2]Bettis E S,Schroeder R W,Cristy G A,et al.Nucl Sci Eng, 1957,2:804–825.

[3]Rosenthal M W,Kasten P R,Briggs R B.Nucl Appl Technol, 1970,8:107–117.

[4]Lapenta G,Mattioda F,Ravetto P.Ann Nucl Energy,2001,28: 1759–1772.

[5]Dulla S,Ravetto P,Rostagno M M.Ann Nucl Energy,2004,31:1709–1733.

[6]Dulla S and Ravetto P.Nucl Sci Eng,2007,155:475–488.

[7]Yamamoto T,Mitachi K,Ikeuchi K,et al.Heat Transfer Asian Res,2006,35:434–450.

[8]YamamotoT,MitachiK,SuzukiT.JSMEIntJB-FluidT,2005,48:610–617.

[9]Suzuki N and Shimazu Y.J Nucl Sci Technol,2008,45:575–581.

[10]Krepel J,Grundmann U,Rohde U,et al.Ann Nucl Energy, 2005,32:1799–1824.

[11]Krepel J,Rohde U,Grundmann U,et al.Ann Nucl Energy, 2007,34:449–462.

[12]Lecarpentier D.Ph.D.Thesis,National Academy of Arts and Trades,2001.

[13]Lecarpentier D and Carpentier V.Nucl Sci Eng,2003,143: 33–46.

[14]Delpech M,Dulla S,Garzenne C,et al.Proceedings of the international conference GLOBAL,2003,2182–2187.

[15]Lapenta G.Nuclear Reactor Physics,CLUT,Turin,2005, pp.195–210.

[16]Memoli V,Cammi A,Di Marcello V.Proceedings of the COMSOL Conference,Milan,Italy,2009.

[17]Kˇrepel J,Grundmann U,Rohde U.Proceedings of ICONE 12 Conference,Arlington,Virginia(Washington,DC),USA. 2004.

[18]Cammi A,Di Marcello V,Luzzi L,et al.Ann Nucl Energy, 2011,38:1356–1372.

[19]Hill M D and Marty M R.Computer,2008,41:33–38.

[20]GustafsonJ.CommunicationsoftheACM,1988,31:532–533.

[21]Owens J D,Luebke D,Govindaraju N,et al.Comput Graph Forum,2007,26:80–113.

[22]Ruan J and Han D D.Microelectronics&Computer,2009,26: 201–205.(in Chinese)

10.13538/j.1001-8042/nst.25.020601

(Received October 30,2013;accepted in revised form December 18,2013;published online March 20,2014)

?SupportedbytheNationalNatureScienceFoundationof China(Nos.11075057,11035009 and 10979074)

?Corresponding author,ddhan@ee.ecnu.edu.cn