Zhen-kun MA, Zi-wu FAN*, Ming ZHANG, Yi-lu SU

1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P. R. China

2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, P. R. China

3. Administration Office of Feilaixia Water Conservancy Project of Guangdong Province, Qingyuan 511500, P. R. China

Flood risk control of dams and dykes in middle reach of Huaihe River

Zhen-kun MA1, Zi-wu FAN*2, Ming ZHANG2, Yi-lu SU3

1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P. R. China

2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, P. R. China

3. Administration Office of Feilaixia Water Conservancy Project of Guangdong Province, Qingyuan 511500, P. R. China

Three stochastic mathematical models for calculation of the reservoir flood regulation process, river course flood release, and flood risk rate under flood control were established based on the theory of stochastic differential equations and features of flood control systems in the middle reach of the Huaihe River from Xixian to the Bengbu floodgate, comprehensively considering uncertain factors of hydrology, hydraulics, and engineering control. They were used to calculate the flood risk rate with flood regulation of five key reservoirs, including the Meishan, Xianghongdian, Nianyushan, Mozitan, and Foziling reservoirs in the middle reach of the Huaihe River under different flood frequencies, the flood risk rate with river course flood release under design and check floods for the trunk of the Huaihe River in conjunction with relevant flood storage areas, and the flood risk rate with operation of the Linhuaigang Project under design and check floods. The calculated results show that (1) the five reservoirs can withstand design floods, but the Xianghongdian and Foziling reservoirs will suffer overtopping accidents under check floods;

stochastic mathematical model; reservoir flood regulation; river course flood release; risk factor; risk rate; middle reach of Huaihe River

1 Introduction

Risk analysis is a comprehensive interdisciplinary subject developed in recent decades. The risk analysis of water conservancy projects originated in the U.S.A. In 1978, theinstruction of the National Water Resources Committee emphasized the necessity and importance of system risk analysis in water conservancy projects (Xie 2006). Europe established a specialized agency for engineering reliability and risk analysis, and thereafter put forward a research framework on the system theory and evaluation method and index. In recent years, Canada, the U.K., Finland, Sweden, Holland, and other countries have developed research on evaluation of dam safety and consequent decision making, and put forward a series of theories and methods for analysis of dam safety.

Evaluation of the flood risk rate with flood regulation of dykes and dams is not only correlated to the selection of flood regulation policies but also to the safety of the protected area. Its reasonable calculation is of significance to scientific research and guidance for flood control (Humberto 1996). The flood risk rate of a dyke or dam is the probability of overtopping accidents during its service life (Jiang et al. 2005; Kuo et al. 2007; Kwon and Moon 2006; Tung and Mays 1980). The flood regulation capacity of a reservoir is affected by uncertain hydrological and hydraulic factors, including the process of upstream inflow floods, flood discharge capacity, the relation between flood storage capacity and water level, and the initial regulation water level. The flood routing process of a river course is influenced by various uncertain input factors, including initial conditions of water level of cross-sections, channel roughness, channel geometric configuration, and partial resistance (Yen 1970). Those random factors determine the randomness of the flood regulation process of reservoirs and the flood water surface profile of river courses.

The key to understanding the flood risk of dykes and dams is to calculate the probability distribution and characteristic parameters of the upstream water level of reservoirs and the water level of river courses by establishing stochastic models for reservoir flood regulation and river course flood release based on the theory of stochastic differential equations, which comprehensively consider various random factors during reservoir flood regulation and river course flood release.

Flood control in the Huaihe River Basin has drawn wide attention in the water conservancy management and research field because of the basin’s extreme complexity in climate, hydrology, landforms, and elevation (Qian 2003; Qian 2009, 2008; Qian et al. 2004). In this study, stochastic mathematical models and methods for calculating the flood risk rate with reservoir flood regulation and river course flood release were established with respect to the medium-size and large key reservoirs and dykes of the flood control system for the reach from Xixian to the Bengbu floodgate in the middle reach of the Huaihe River (Fig. 1). The risks with flood regulation of water conservancy projects on the trunk and branches, including several large reservoirs in the middle reach of the Huaihe River, were analyzed, and on such a basis their flood control capacities were evaluated.

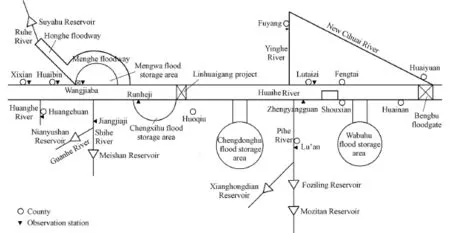
Fig. 1 Distribution of main water conservancy projects in middle and upper reaches of Huaihe River

2 Stochastic models

2.1 Stochastic model for reservoir flood regulation

Throughout the flood regulation process of a reservoir, the uncertain hydrological and hydraulic conditions result in random variations of reservoir water level and corresponding flood discharge capacity, and finally result in the randomness of the maximum reservoir water level related to the flood risk rate (Harris and Brunner 2011; Jiang 1994). The process randomness is not considered in the traditional methods of flood control, and the rationality of reservoir flood control programs and dam safety against floods cannot be accurately evaluated. To describe the flood control process more accurately, it is necessary to consider the influences of various random factors, and the calculation of flood regulation should use the stochastic differential equation instead of the deterministic ordinary differential equation (Chauhan and Bowles 2004; Chu 1992; Liu 2008).

Throughout the flood regulation process, the reservoir flood storage capacity changes randomly. It restricts the random change of reservoir water level and is meanwhile determined by the random processes of flood input and output. The random change process W(t) is the Markov process (Qian 2008) and is characterized by a continuous, stable, and independent increasing process, which fits within the definition of the Wiener process. There are various random factors affecting W(t) during the flood regulation process. The comprehensive effects cause W(t) to randomly vary around the mean process line μW(t), and its probability distribution is normal. Assuming an unbiased Wiener process B(t) on μW(t), W(t) can be expressed as:

where μW(t) is calculated with the traditional deterministic method. The differential form ofEq. (1), divided by G(h ) = d w dh, is as follows:

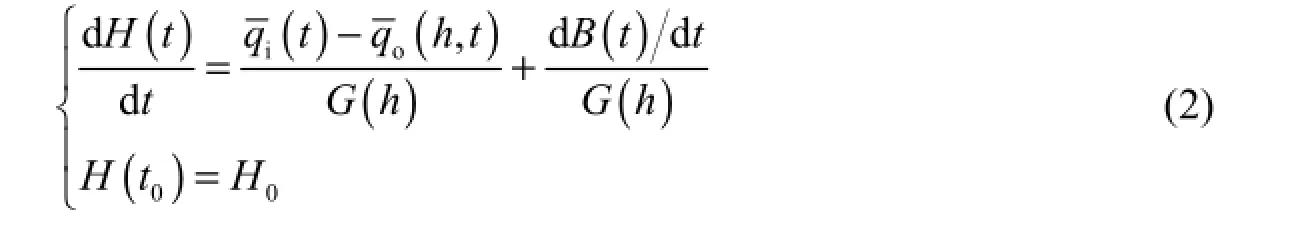
In order to solve the random process ()Ht, the probability density ( ),fht at different times should be obtained based on the probability distribution transfer of the Markov process. Using the Fokker-Planck forward equation, Eq. (2) becomes

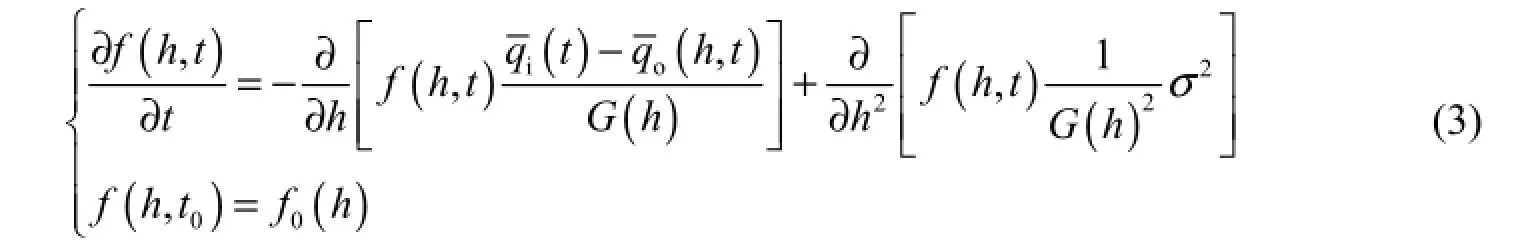
where σ2is the parameter of process density(Jiang et al. 2005). Eq. (3) is a deterministic differential equation and can be solved with the finite difference method (Salas et al. 2003). While the equation is being solved, μH(t ) and σH(t), which are the mean value and standard deviation of water level at time t, respectively, can be calculated synchronously by use of the distribution of f(h ,t), and μqo(t ), the mean value of flood outflow at time t, can be obtained. The randomness of the reservoir water level process H(t) can be quantified and described by f(h ,t) and the corresponding μH(t ) and σH(t) at different times.

2.2 Stochastic model for flood water surface profile of river courses

The randomness of the flood water surface profile of a river course is dependent upon uncertain input factors, such as its roughness, geometric configuration, and partial resistance (Klein et al. 2010; Jiang 1995). By analyzing the features of a dynamic river course system, the random factors affecting the uncertainty of the water surface profile can be divided into three categories: (1) random coefficients: the roughness of the river course is the most important random parameter; (2) random initial conditions: the initial hydraulic condition0Z has a significant influence on the solutions to differential equations, and the flood water surface profile is also affected by some other uncertain factors such as the flow discharge of the river course; and (3) random terms: any error generated in calculating the water head, partial loss, sectional area, and wetted perimeter may cause random fluctuation of the water surface profile.

The comprehensive effects of various random input factors causes the hydraulic condition of the river course Z(x ,n) to randomly change around the mean value process line μZ(x), where x is the distance along the river course, nis Manning’s roughness. The probability distribution f(z ,x) can be assumed to be a normal one. Thus, it is considered that Z(x ,n)obeys the definition conditions of the Wiener process. When the mean deviation of Z(x ,n) is deduced, there is still an unbiased water level change process l(x), with a mean value of μl= 0, and varianceTherefore, a nonhomogeneous random term can be introduced into the river course water surface profile equation:

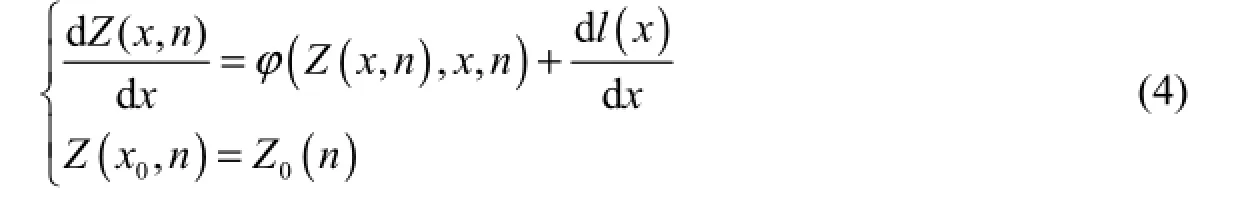
where ?(Z (x ,n ),x,n )= Q2K2, which is the water surface profile calculated by the deterministic method. Q is the flow discharge of the river course;where R is the hydraulic radius, and A is the area of the cross-section.

The Fokker-Planck forward equation provides a way to solve the probability density of Z(x,n). After it is processed, Eq. (4) is transformed into an Ito equation, which can be simplified into the following:

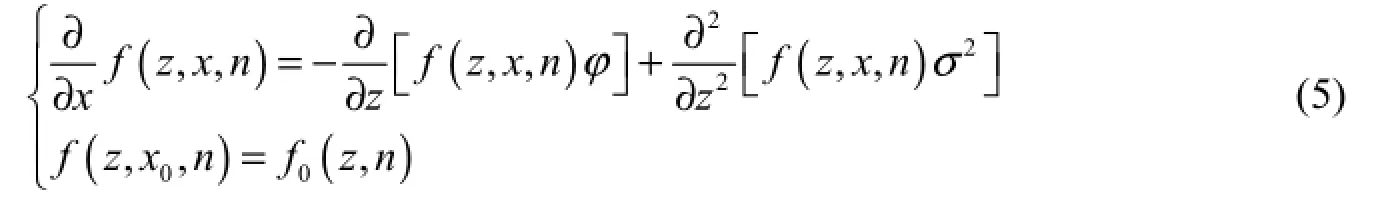
wherezis the water level of the river course and f(z ,x,n) is the probability density. Eq. (5) is a deterministic differential equation that can be solved with the finite difference method. Once f(z,x,n) is obtained, f(z,x) can be obtained with the numerical integration of roughness, and then the random process of the flood water surface profile of the river course can be calculated with the integration of water level z.

3 Method of calculating flood risk rate with flood regulation of dykes and dams

For a specific flood event, the probability calculation of flood overtopping conditions is basically the problem of the relation between flood force F (i.e., the reservoir water level or river course flood water level) and flood control resistance D (i.e., the dyke or dam elevation) (Jiang et al. 2005; Salas et al. 2003; Gebregiorgis and Hossain 2012).

3.1 Calculation of flood risk rate under specific frequency

For floods with specific return periods and operating conditions, the probability of flood overtopping (fP) can be described as

Eq. (6) shows that the main random factors affecting the flood risk rate are D and F.

The uncertainty of the dyke or dam elevation D is easy to analyze. The randomness of D is caused by construction measurement errors and wind waves in reservoirs and river courses. Generally, it is considered to have a normal distribution: the mean valueDμ can be the design elevation, and the standard deviationDσ is relatively small.

The water levels of reservoirs and river courses are random processes. Using the method mentioned above, ( ),fht and the correspondingHμ andHσ values of a reservoir at different times or (,)fzx and the corresponding mean valuezμ and standard deviationzσ of the water level of a river course at different positions can be obtained. In this way, the conditions for calculating the flood risk rate with flood regulation of reservoirs and river course flood release are obtained.

3.2 Calculation of mean annual flood risk rate of flood control project

To obtain the general overtopping risk rate for a flood control project, it is necessary to consider all probable flood levels.

The occurrence of a flood event is the precondition of the flood risk rate. The total flow discharge of all probable floods is divided into those of numerous areas, and each area has a certain flow discharge qdwith a corresponding probability density f(qd). The summation of the probability for all the flood events is

The overtopping risk rate of a dyke or dam project within one year can be expressed as

where P is the flood frequency, and1P is the mean overtopping risk rate of the flood control project within one year.

4 Analysis of flood risk control of dykes and dams in middle reach of Huaihe River

The stochastic model for flood water level regulation of reservoirs was used to calculate the flood risk rate with flood regulation of the Meishan, Xianghongdian, Nianyushan, Mozitan, and Foziling reservoirs, in the middle reach of the Huaihe River, under different design flood frequencies. The stochastic model for the flood water surface profile of river courses was used to calculate and evaluate the flood risk rate of the reach from Xixian to the Bengbu floodgate, considering the integrated application of flood storage areas, dams, and floodgates under design floods.

4.1 Reservoir projects

The five key reservoirs are designed with the capacity to withstand design floods with return periods of 100 to 500 years. Except for the Mozitan Reservoir, these reservoirs are also designed with the capacity to withstand check floods with a return period of 5000 years. They play important roles in flood control of the Huaihe River Basin (HWCRDI 2003). The flood risk rates with flood regulation of the reservoirs under different flood frequencies were calculated and analyzed, and their flood control capacities were also evaluated.

4.1.1 Analysis of flood regulation at Meishan Reservoir

Due to the limitations of text length, only the results relating to the Meishan Reservoir were analyzed in detail. The Meishan Reservoir has a total capacity of 2.264 km3, which was originally designed for a design flood with the flood return period of 1 000 years and a check flood with the flood return period of 10 000 years. In 2002, the flood control standard was rechecked and modified. Its capacity was then shown to be adequate for a design flood with the flood return period of 500 years and a check flood with the flood return period of 5 000 years. The maximum design water level, which we refer to below as the limit water level, of the reservoir is 125.27 m, and the dam crest elevation is 140.17 m. Its main purposes are flood control, irrigation, power generation, navigation, and aquatic production, and it is also designed for flood storage in the trunk of the Huaihe River. Fig. 2 shows the hydrographs of inflow floods of the Meishan Reservoir with different frequencies.

Fig. 2 Hydrographs of inflow floods of Meishan Reservoir with different flood frequencies

(1) Influence of initial water level:

The mean value of the initial water level0zμ was modified, and five values of0zμ , 124.27 m, 124.77 m, 125.27 m, 125.77 m, and 126.27 m, were selected for calculation.

Fig. 3 shows the hydrographs of the mean value of the water level in the Meishan Reservoir with different mean values of initial water levels. Table 1 gives the mean value and standard deviation of the maximum water level and the maximum flood risk rate with flood regulation of the Meishan Reservoir for different mean values of initial water levels.

The mean value of the initial water level of the Meishan Reservoir has a strong influence on the distribution of the water level at the initial stage, and, in general, the influence gradually decreases with time. The reason is that the rise of the water level will increase the flood discharge, and these joint effects weaken the influence of the water level on the flood risk rate with reservoir flood regulation. If the mean value of the initial water level is 1.0 m higher than the limit water level of 125.27 m, the mean value of the maximum water levelonly increases 0.02 m, and the risk rate with flood regulation increases by 0.3%, showing that the initial water level of reservoirs has little effect on the mean value of the maximum water level and flood risk rate, and the Meishan Reservoir has a high capacity for flood regulation.

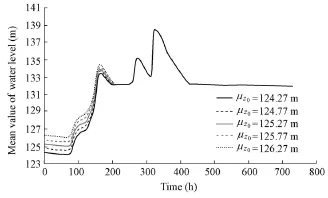
Fig. 3 Hydrographs for different mean values of initial water level in Meishan Reservoir

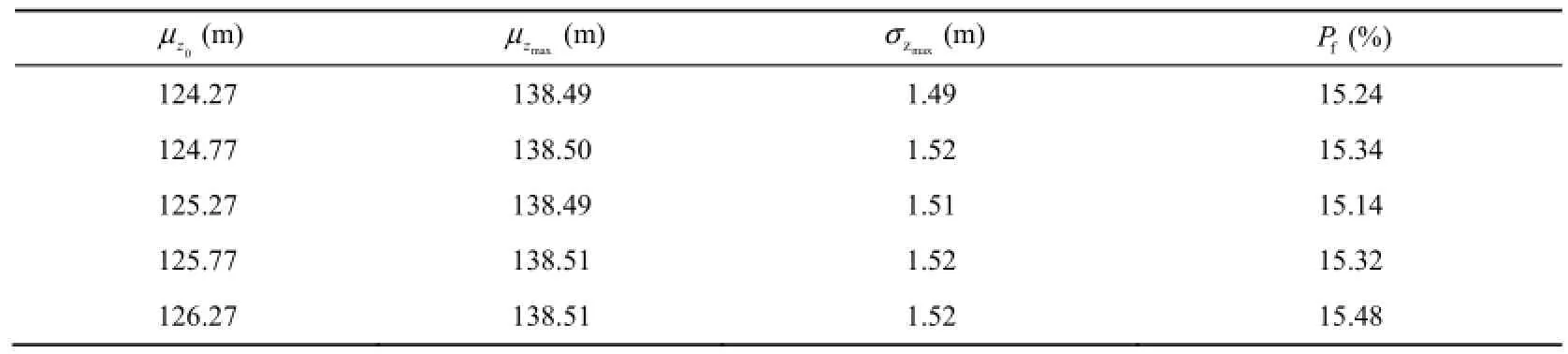
Table 1 Results of flood regulation of Meishan Reservoir with different mean values of initial water level

(2) Influence of flood frequency on flood risk rate with flood regulation:

To analyze the flood regulation of the Meishan Reservoir under floods of different return periods, six flood frequencies, 0.01%, 0.02%, 0.05%, 0.10%, 0.20%, and 1.00%, were selected, with flood regulation beginning at the limit water level of 125.27 m, and the probability distribution of the water level and final flood risk rate under flood regulation were calculated using the proposed model. Fig. 4 shows the mean value and standard deviation of the water level with flood regulation of the Meishan Reservoir under a check flood with the flood return period of 5 000 years. Fig. 5 shows the mean value of the water level with flood regulation at different flood frequencies. Table 2 shows the results of flood regulation of the Meishan Reservoir with different flood frequencies.

The calculated results show that the flood risk rate with flood regulation of the Meishan Reservoir is related to the frequency of reservoir inflow floods, and a smaller flood frequency means a larger flood risk rate. For a flood with a frequency of 0.05%, the mean value of the maximum water level is 139.33 m, which is below the dam crest elevation of 140.17 m, but this does not mean there is no risk, as the standard deviation of the maximum water level is1.6 m, and the maximum flood risk rate with reservoir flood regulation is 31.26%. When adesign flood with the return period of 5 000 years occurs, the flood risk rate with reservoirflood regulation increases to 52.19%, and the probability of flood overtopping exceeds 50%. The Meishan Reservoir has a high capacity for flood regulation, and a scientific regulation process can effectively withstand a flood with a return period of 2 000 years.

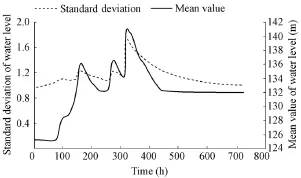
Fig. 4 Mean value and standard deviation of water level with flood regulation of Meishan Reservoir under check flood with flood return period of 5 000 years

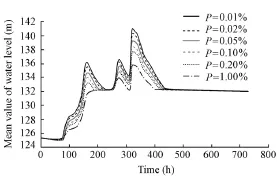
Fig. 5 Distribution of mean value of water level with flood regulation of Meishan Reservoir at different flood frequencies

Table 2 Characteristic values of flood risk rates with flood regulation of Meishan Reservoir under check flood at different flood frequencies

4.1.2 Analysis of flood regulation in other reservoirs

Fig. 6 showsf-PP curves and corresponding overtopping risk rates of all five reservoirs at different flood frequencies. Table 3 provides the mean values of the maximum water level and the corresponding overtopping risk rates with flood regulation of the other four reservoirs, the Xianghongdian, Nianyushan, Moztitan, and Foziling reservoirs, at different flood frequencies.

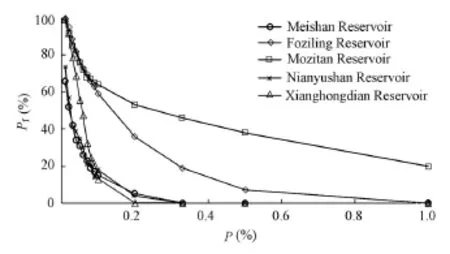
Fig. 6 f-PPcurves with flood regulation of five reservoirs

The maximum flood risk rates of the Meishan, Xianghongdian, Nianyushan, Mozitan, and Foziling reservoirs are 4.50%, 0.00%, 0.00%, 19.82%, and 0.00%, respectively, under the design flood, and 52.19%, 92.21%, 57.28%, 63.57%, and 95.44%, respectively, under the check flood at the flood frequency of 0.02%. Thus, the five reservoirs can effectively withstand the design flood. However, the Xianghongdian and Foziling reservoirs are at risk of overtopping accidents under check floods, as their actual flood control capacities are far below the standard against check floods. The mean annual overtopping risk rates of the five reservoirs are 4.8%, 6.4%, 5.2%, 52%, and 20%, respectively.

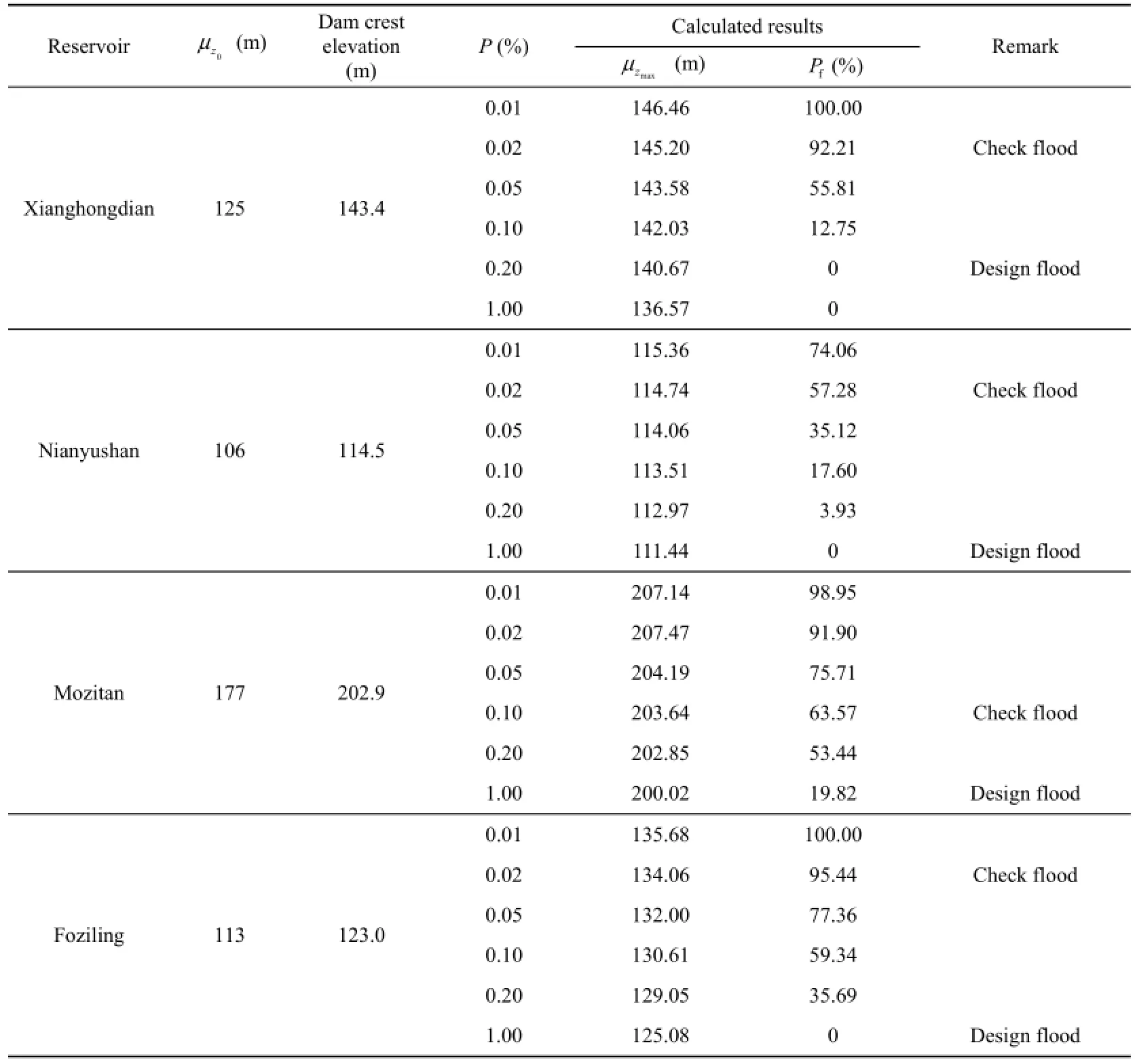
Table 3 Results of flood risk rates with flood regulation at different flood frequencies

4.2 Dyke projects

The proposed stochastic mathematical model for river course flood release was used to calculate the flood risk rate by sections with river course flood release and to evaluate the flood carrying capacity of each section in the middle reach of the Huaihe River from Xixian tothe Bengbu floodgate under a design flood with the flood return period of 20 years, considering the application of flood storage areas and the influence of local inflow.

To avoid error accumulation in calculating the flood risk rate, the middle reach of the Huaihe River was further divided into five reaches: Xixian-Huaibin, Huaibin-Wangjiaba, Wangjiaba-Runheji, Runheji-Zhengyangguan, and Zhengyangguan-Bengbu floodgate. In consideration of the special function of the Linhuaigang Project, the flood risk rate of the reach from Runheji to Zhengyangguan was calculated by means of the model for the flood risk rate with reservoir flood regulation, and the risk rate of the Linhuaigang Project was calculated under a design flood with the flood return period of 100 years and under a check flood with the flood return period of 1 000 years.

4.2.1 Calculation of flood risk rate of reach from Wangjiaba to Runheji under river course flood release

The reach from Wangjiaba to Runheji is about 20 km long, including the Mengwa flood storage area, Menghe floodway, and Shihe and Guanhe rivers (HWCC 2007). In the calculation, when the inflow flood to Wangjiaba was 7 000 m3/s under the design flood, 2 500 m3/s would flow along the trunk of the Huaihe River, 1 626 m3/s would flow into the Mengwa flood storage area, and 2 874 m3/s would flow into the Menghe floodway. Downstream of Wangjiaba, there was 400 m3/s of water from the Shihe and Guanhe rivers flowing into the trunk of the Huaihe River. Therefore, a total flow discharge of 2 900 m3/s flowed downstream. If the flood in the Menghe floodway flowed into the Huaihe River, the total flow discharge would be 7 400 m3/s.

The stochastic mathematical model was used to calculate the flood risk rate of the reach from Wangjiaba to Runheji with flood control under the design flood. The results are given in Table 4 and Fig. 7. The mean value of the river course roughnessnμ= 0.022, and the mean value of the initial water level0zμ = 27.1 m. The flood risk rate of the reach from Wangjiaba to Runheji ranges from 0.12 to 0.31, with a large degree of fluctuation, and the mean risk rate is around 0.20.

Table 4 Flood risk rates with flood control of reach from Wangjiaba to Runheji under design flood with flood return period of 20 years

Fig. 7 Results of flood routing for river reach from Wangjiaba to Runheji

4.2.2 Results of flood regulation of Linhuaigang Project

The reach from Runheji to Zhengyangguan, which is affected by the Linhuaigang Project, is characterized by reservoir flood regulation and river course flood release at high flood levels, so the two stochastic methods for reservoir flood regulation and river course flood release were used to calculate the flood risk rate with flood control of the Linhuaigang Project. The results are compared below:

(1) Risk analysis based on random flood regulation process of Linhuaigang Project:

Through use of the stochastic mathematical model for reservoir flood regulation, the distributions of the mean value and standard deviation of the water level throughout the flood regulation process can be obtained, and the flood risk rate with reservoir flood regulation can also be calculated. Under the design flood conditions with the flood return period of 100 years, the mean value of the maximum water level in front of the Linhuaigang Dam is 28.02 m, which is 0.39 m lower than the limit water level; the standard deviation of the maximum water level is 0.35 m; and the maximum flood risk rate with reservoir flood regulation is 0.08. Under the check flood conditions with the flood return period of 1 000 years, the mean value of the maximum water level in front of the Linhuaigang Dam is 29.13 m, and the maximum flood risk rate with reservoir flood regulation is 0.14.

(2) Risk analysis based on random flood release process of river courses:

With respect to the design flood with the flood return period of 100 and check flood with the return period of 1 000 years, the control parameters for calculation of the flood risk rate of the river course with flood control were as follows: for floods with return periods of 100 years and 1 000 years, the initial water levels at Zhengyangguan were both the design water level of 26.5 m; the initial water levels in front of the Linhuaigang Project were the design water levels of 28.41 m and 29.49 m, respectively, and the corresponding flow discharges were, respectively, 10 000 m3/s and 12 000 m3/s; and the design flow discharges at the Jiangtanghu Gate and Linhuaigang Gate were, respectively, 2 400 m3/s and 7 362 m3/s.

Through use of the stochastic model of river course flood release, the upstream mean values of the water level were found to be 27.41 m and 29.51 m, and correspondingovertopping risk rates were 0.06 and 0.09, respectively, under the design flood with the flood return period of 100 years and check flood with the flood return period of 1 000 years.

(3) Flood risk rate for reach from Runheji to Zhengyangguan under effects of Linhuaigang Project and river course flood release:

Under the design flood conditions, considering the function of the Linhuaigang Project, the variations of the mean value and standard deviation of the water level are shown in

Fig. 8(a), and the calculated the flood risk rate and reliability index with flood control in the reach from Runheji to Zhengyangguan are shown in Fig. 8(b). With the operation of the Linhuaigang Project, the flood risk rates of the reach from Runheji to Zhengyangguan were 0.01 to 0.06 and 0.01 to 0.09, respectively, under the design flood conditions with the flood return period of 100 years and the check flood conditions with the flood return period of

1 000 years.

Fig. 8 Results of flood regulation of Linhuaigang Project under design flood

There are some differences between the two model results. The reason is that a reservoir is mainly used for flood regulation, and the flood risk rate with reservoir flood regulation is the probability that the water level in front of the dam is higher than its limit water level, while the flood risk rate under flood release of a river course is obtained by calculating the probability distribution of the flood water surface profile under the deterministic flood discharge under the design water conditions. Nevertheless, the differences between the calculated results of two models are small, and both values are low, indicating that the Linhuaigang Project has a large flood regulation capacity.

4.2.3 Results of flood risk rates with flood control of other reaches

The calculated results show that (1) the mean flood risk rate under flood release of the reach from Xixian to Huaibin is about 0.25, with the flood risk rate varying from 0.20 to 0.30; (2) the flood risk rate under flood release of the reach from Huaibin to Wangjiaba ranges from 0.15 to 0.20, with a mean value of about 0.17, and the risk rate is low and relatively stable; (3) for the reach from Zhengyangguan to the Bengbu floodgate, owing to the complicated landforms, numerous branches, and water conservancy projects, the flood risk rate under flood release of the reach shows a sharp fluctuation, especially upstream of Fengtai where there isno flood storage area, and floods only travel along the river course and flood plain, and the risk rate distinctly increases to about 0.25. Downstream of Fengtai, floods are effectively diverted or retained by numerous flood storage areas.

5 Conclusions

With respect to the features of flood control systems in the middle reach of the Huaihe River, and considering uncertain hydrological and hydraulic factors, statistical mathematic models were used to calculate flood risk rates with reservoir flood regulation and river course flood release for flood control analysis of five key reservoirs, main river courses, and the Linhuaigang Project in the middle reach of the Huaihe River under design and check floods of different flood frequencies. The calculated results show the following:

(1) With reservoir flood regulation, the mean value of the initial water level has significant effects on the distribution of the water level at the early stage of flood regulation, and the comprehensive effect gradually weakens with the increase of time, due to the interaction between the increases of the initial water level and the relative discharge of reservoirs. The mean value of the maximum water level and flood risk rate of reservoirs are proportional to the flood return period, while the initial water level of reservoirs has little effect on the mean value of the maximum water level and flood risk rate. All five reservoirs can effectively withstand the design flood, but under the check flood, there will be a high probability of overtopping accidents. The Xianghongdian and Foziling reservoirs will definitely suffer overtopping accidents. Thus, suitable heightening or reinforcing measures should be taken for these reservoirs.

(2) The mean flood risk rate with flood regulation of dykes and dams from Xixian to the Bengbu floodgate is about 0.2. The dykes along the trunk of the Huaihe River can generally meet the requirements for design floods. For the reach without a flood storage area, where the floods only travel along the river course and the flood plain, the risk rate distinctly increases, while, for the reach with a flood storage area, the floods are effectively diverted or retained.

(3) The proposed stochastic models for reservoir flood regulation and river course flood release were employed to calculate the flood risk rates with flood control of the Linhuaigang Project. The results of the two models show that the application of the Linhuaigang Project in the flood control system of the Huaihe River Basin has strongly reinforced the flood control capacity of the trunk of the Huaihe River.

Chauhan, S. S., and Bowles, D. S. 2004. Dam safety risk assessment with uncertainty analysis. ANCOLD Bulletin, 127, 73-88

Chu, X. Y. 1992. Study on hydraulic uncertainty model. Journal of Hydraulic Engineering, 37(5), 33-38. (in Chinese)

Gebregiorgis, A. S., and Hossain, F. 2012. Hydrological risk assessment of old dams: A case study on Wilson Dam of Tennessee River Basin. Journal of Hydrologic Engineering, 17(1), 201-212. [doi:10.1061/(ASCE)HE.1943-5584.0000410]

Harris, J., and Brunner, G. 2011. Approximating the probability of the probable maximum flood. World Environmental and Water Resources Congress 2011. 3695-3702. ASCE. [doi:10.1061/41173(414)387].

He’nan Water Conservancy Reconnaissance and Design Institute (HWCRDI). 2003. Verification of Safety Standard for Flood Control in Nianyushan Reservoir. Zhengzhou: He’nan Water Conservancy Reconnaissance and Design Institute. (in Chinese)

Huaihe Water Conservancy Committee (HWCC). 2007. Manual of Water Conditions for Flood Control in Huaihe River Basin. Zhengzhou: Huaihe Water Conservancy Committee. (in Chinese)

Humberto, M. M. 1996. Flood safety analysis. International Water Power and Dam Construction, 48(5), 21-24.

Jiang, S. H. 1994. Application of stochastic differential equations in risk analysis for flood relief. Journal of Hydraulic Engineering, 39(3), 1-9. (in Chinese)

Jiang, S. H. 1995. Risk analysis of flood flow in river by using stochastic differential equation. Scientific Research of Water Conversancy and Water Transportation, (2), 127-136. (in Chinese)

Jiang, S. H., Fan, Z. W, and Wu, S. Q. 2005. Flood Disaster Risk Evaluating and Flood Control Safety Decision Making. Beijing: China Waterpower Press. (in Chinese)

Klein, B., Pahlow, M., Hundecha, Y., and Schumann, A. 2010. Probability analysis of hydrological loads for the design of flood control systems using copulas. Journal of Hydrologic Engineering, 15(5), 360-369. [doi:10.1061/(ASCE)HE.1943-5584.0000204]

Kuo, J. T., Yen, B. C., Hsu, Y. C., and Lin, H. F. 2007. Risk analysis for dam overtopping: Feitsui Reservoir as a case study. Journal of Hydraulic Engineering, 133(8), 955-963. [doi:10.1061/(ASCE)0733-9429(2007) 133:8(955)].

Kwon, H. H., and Moon, Y. I. 2006. Improvement of overtopping risk evaluations using probabilistic concept for existing dams. Stochastic Environmental Research and Risk Assessment, 20(4), 223-237. [doi:10.1007/ s00477-005-0017-2].

Liu, Y. L. 2008. Uncertainty Analysis of Rainfall-runoff Models and Risk Assessment of Reservoir Flood Control. Ph. D. Dissertation. Dalian: Dalian University of Technology. (in Chinese)

Qian, M. 2008. Huaihe River flood control and regulation in 2007. Water Resources and Hydropower Engineering, 39(1), 12-15. (in Chinese)

Qian, M. 2009. Synchronous development of Huaihe River control and New People’s Republic of China. Huaihe River Control, 10, 4-6. (in Chinese)

Qian, M. K. 2003. Huaihe River flood control emergency system. Office Automation, (12): 37-38. (in Chinese)

Qian, M. K., Xu, S. J., Wang, S. X., and Wang, J. T. 2004. Study on the probability flood forecasting model at Xixian Gauging Station of Huaihe River Basin. Hydrology, 24 (2), 23-26. (in Chinese) [doi:10.3969/ j.jssn.1000-0852.2004.02.006]

Salas, J. D., Burlando P., Heo, J. H., and Lee, D. J. 2003. The axis of risk and uncertainty in hydrologic design. Proceedings of Hydrology Days 2003, 153-164.

Tung, Y. K., and Mays, L. W. 1980. Risk analysis for hydraulic design. Journal of the Hydraulics Division, 106(5), 893-913.

Xie, G. Q. 2006. Flood Risk Analysis of the Reservoir in the Arid Area. M. E. Dissertation. Shihezi: Shihezi University. (in Chinese)

Yen, B. C. 1970. Risk in hydrologic design of engineering project. Journal of the Hydraulics Division, 96(4), 959-966.

(Edited by Ye SHI)

——

This work was supported by the National Natural Science Foundation of China (Grant No. 51139001).

*Corresponding author (e-mail: zwfan@nhri.cn)

Received May 2, 2013; accepted Nov. 16, 2013

(2) considering the service of flood storage areas under the design flood conditions of the Huaihe River, the mean flood risk rate with flood regulation of dykes and dams from Xixian to the Bengbu floodgate is about 0.2, and the trunk of the Huaihe River can generally withstand design floods; and (3) under a check flood with the flood return period of 1 000 years, the risk rate of overtopping accidents of the Linhuaigang Project is not larger than 0.15, indicating that it has a high flood regulation capacity. Through regulation and application of the flood control system of the Linhuigang Project, the Huaihe River Basin can withstand large floods, and the safety of the protected area can be ensured.