殷承元

(上海財(cái)經(jīng)大學(xué)應(yīng)用數(shù)學(xué)系,上海 200433)

帶Brown運(yùn)動的隨機(jī)奇異積分的存在性

殷承元

(上海財(cái)經(jīng)大學(xué)應(yīng)用數(shù)學(xué)系,上海 200433)

在軌跡二階導(dǎo)數(shù)具有H¨older連續(xù)的條件下,利用高階奇異積分思想和概率極限的理論,研究了在Brown運(yùn)動下的隨機(jī)奇異積分.得到了以Brown運(yùn)動為積分元的隨機(jī)奇異積分是存在性定理.

隨機(jī)奇異積分;Brown運(yùn)動;隨機(jī)基

1 引言

奇異積分理論和應(yīng)用非常重要,文獻(xiàn)[1-2]做過了大量開創(chuàng)性工作.隨機(jī)積分也日益發(fā)展[3].文獻(xiàn)[4]討論了簡單的隨機(jī)奇異積分.本文在文獻(xiàn)[5-6]基礎(chǔ)上,探討在Brown運(yùn)動下的一類奇異積分.

設(shè)?是一個(gè)完備的概率空間,其中A是?上的一個(gè)σ-代數(shù),P是關(guān)于這個(gè)σ-代數(shù)的概率測度.記F是滿足通常條件的過濾,(?A,P,F)是隨機(jī)基,Wt=W(t,ω),t∈R+是Brown運(yùn)動.

設(shè)過濾F在時(shí)刻t的σ-代數(shù)為Ft,f(t,τ,ω)是R+×R×?,上的函數(shù),對每個(gè)t≥0, f(t,τ,ω)關(guān)于σ(B[0,t]×B(R)×Ft)可測.本文將討論下列的奇異積分:

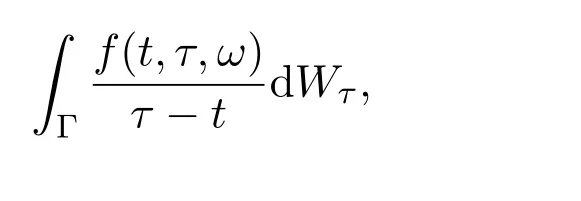
這里Γ是R+中的區(qū)間.通常情況下,

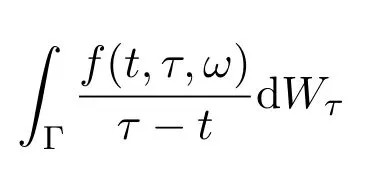
是發(fā)散.本文將利用高階奇異積分的思想引入這個(gè)帶Brown運(yùn)動的奇異積分.

2 結(jié)果與證明

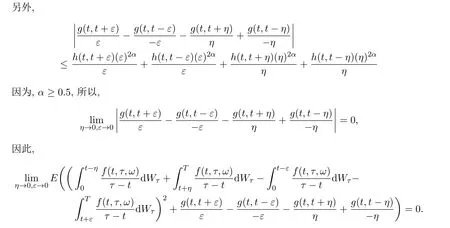
[1]路見可.解析函數(shù)邊界問題[M].武漢:武漢大學(xué)出版社,2009.

[2]Du Jinyuan.Singular integral operators and singular quadrature operators associated with singular integral equations[J].Acta.Math.Sci.,1998,18(2):227-240.

[3]P′eter Medvegyev.Stochastic Integration Theory[M].Oxford:Oxford University Press,2007.

[4]王傳榮.隨機(jī)奇異積分的存在定理[J].福州大學(xué)學(xué)報(bào):自然科學(xué)版,2004,32(4):393-396.

[5]殷承元.閉復(fù)超球上的普里瓦洛夫定理[J].安徽大學(xué)學(xué)報(bào):自然科學(xué)版,1990,14(3):6-11.

[6]殷承元.第三類典型域上的Cauchy型積分[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2002,18(1):6-20.

Existence of singular integral with Brown motion

Yin Chengyuan
(Applied Mathematics Department,Shanghai University of Finance&Economics,Shanghai200433,China)

In the note,random singular integral with Brown motion is investigated.If the second derivative of the integrand is H¨older continuous,by the theories of higher singular integral and limit with respect to probability,the random singular integral with integrator of Brown motion exists in probability limit.

random singular integral,Brown motion,stochastic basis

O211

A

1008-5513(2013)03-0221-05

10.3969/j.issn.1008-5513.2013.03.001

2013-03-15.

國家自然科學(xué)基金(11271240);上海財(cái)經(jīng)大學(xué)211工程項(xiàng)目.

殷承元(1958-),博士,教授.研究方向：基礎(chǔ)數(shù)學(xué)與概率.

2010 MSC:47B06,47B38