楊海霞

(1.西北大學(xué)數(shù)學(xué)系,陜西西安 710069;2.西北大學(xué)非線性研究中心,陜西西安 710069)

一個組合方程的單孤子解和周期尖波解

楊海霞1,2

(1.西北大學(xué)數(shù)學(xué)系,陜西西安 710069;2.西北大學(xué)非線性研究中心,陜西西安 710069)

構(gòu)造一個組合方程的單孤子解和周期尖波解.應(yīng)用格林函數(shù)的性質(zhì),以及求一個非線性偏微分方程(簡稱PDE)弱解的方法.求出了這個組合方程的單孤子解和周期尖波解,推廣了前人的研究成果.

Camassa-Holm方程;modified Camassa-Holm方程;Novikov方程;孤子解;周期尖波解

1 引言

在近幾十年來,很多學(xué)者對Camassa-Holm(簡稱CH)方程,modified Camassa-Holm(簡稱mCH)方程和Novikov方程進(jìn)行了深入研究,通過求出它們的單孤子解,多孤子解和周期尖波解,從而對它們的性質(zhì)進(jìn)行了研究,比如它的拉克斯對,雙哈密頓結(jié)構(gòu),進(jìn)而得到了它們的可積性.還有像解的爆破性,穩(wěn)定性問題,從而可以看出,要研究一個新的方程,方程的解的問題占據(jù)著重要意義.

已經(jīng)知道CH方程有孤子解[1-4]u=ae-|x-ct|,(c＞0)和周期尖波解[5-8]

的周期尖波解.于是,猜測這個組合方程也應(yīng)該有形如這樣的解,通過運用求弱解的方法[1,8-9],證實了猜想,并且求出了這個組合方程的單孤子解和周期尖波解.

2 組合方程的孤立波解

3 組合方程的周期尖波解

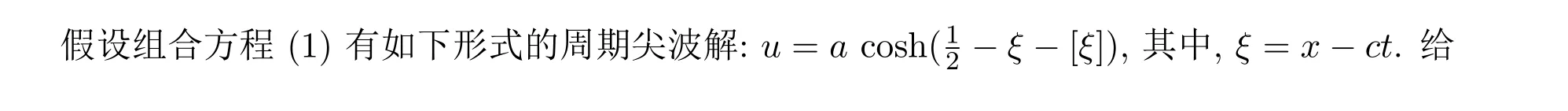
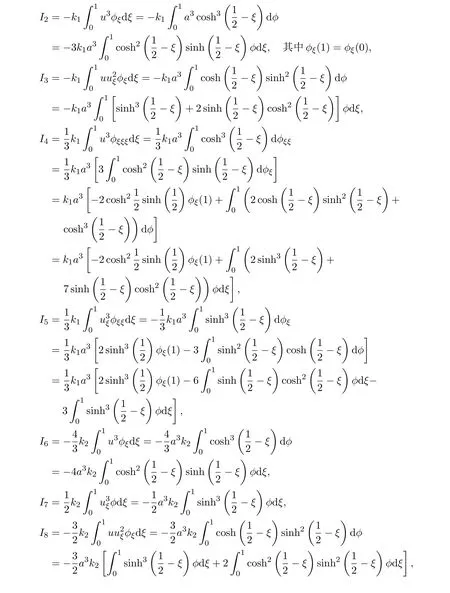
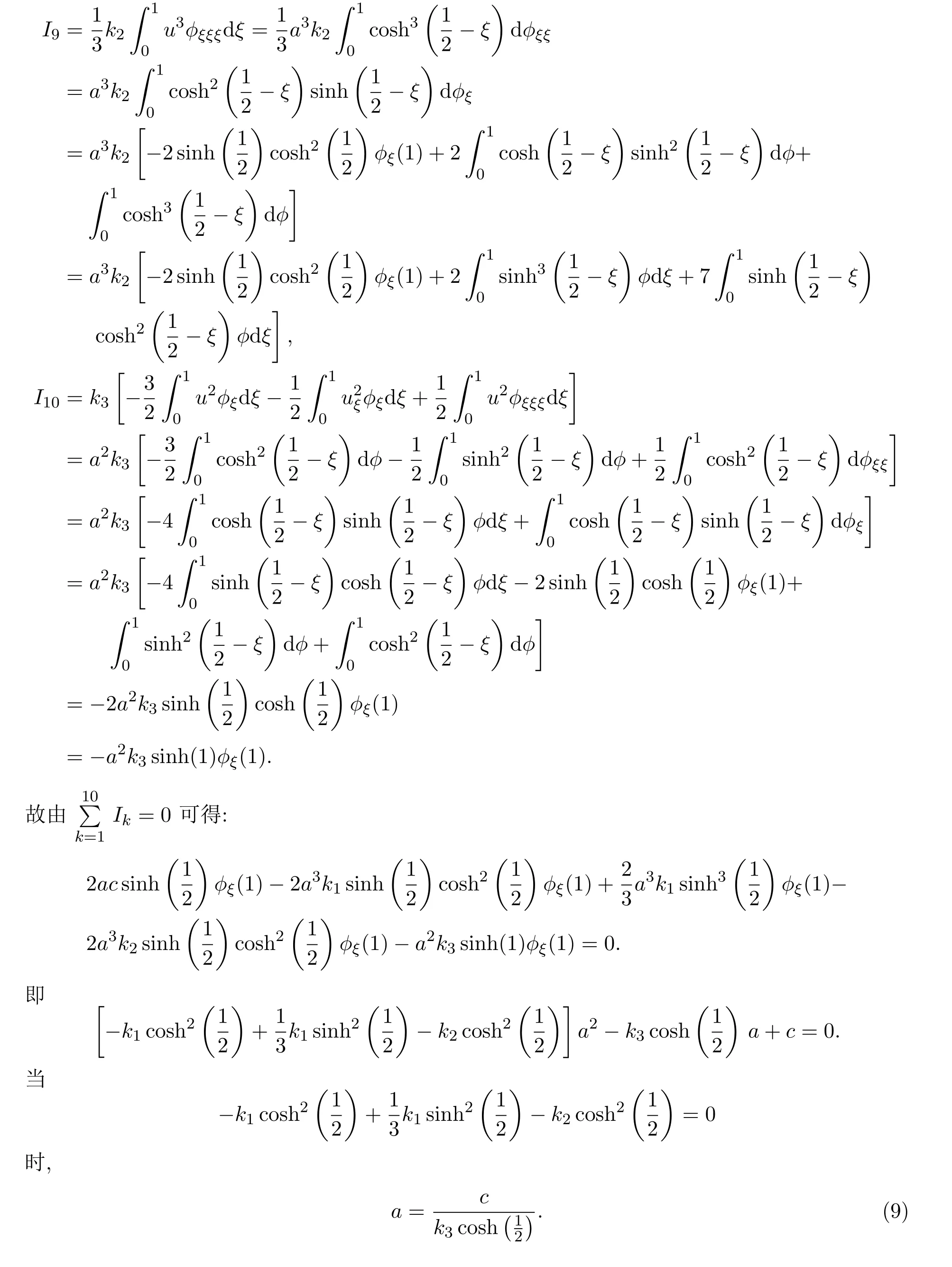
4 結(jié)論

通過運用求弱解的方法以及格林函數(shù)的性質(zhì),求出了一個新的組合方程的單孤子解和周期尖波解,這對于以后進(jìn)一步研究它的其它性質(zhì)(比如它的拉克斯對,雙哈密頓結(jié)構(gòu)等)都有著不可或缺的作用.

[1]Constantin A,Molinet L.Global weak solutions for a shallow water equation[J].Communications in Mathematical Physics,2000,211(1):45-61.

[2]Degasperis A,Holm D D,Hone A N W.A new integrable equation with peaked solitons[J].Theoretical and Mathematical Physics,2002,133(2):1463-1474.

[3]Camassa R,Holm D D.An integrable shallow water equation with peaked solitons[J].Physical Review Letters,1993,71(11):1661-1664.

[4]Lenells J.Traveling wave solutions of the Camassa-Holm equation[J].Journal of Differential Equations, 2005,217(2):393-430.

[5]Fu Y,Liu Y,Qu C Z.Well-posedness and blow-up solution for a modified two-component periodic Camassa-Holm system with peakons[J].Mathematische Annalen,2010,348(2):415-448.

[6]Boyd J P.Peakons and coshoidal waves:traveling wave solutions of the Camassa-Holm equation[J].Applied Mathematics and Computation,1997,81(2):173-187.

[7]Constantin A.On the cauchy problem for the periodic Camassa-Holm equation[J].Jounal of Differential Equations,1997,141(2):218-235.

[8]Yin Z.Global weak solutions for a new periodic integrable equation with peakon solutions[J].Journal of Functional Analysis,2004,212(1):182-194.

[9]Gui G,Liu Y,Olver P J,et al.Wave-breaking and peakons for a modified Camassa-Holm equation[J]. Communications in Mathematical Physics,2012,200(1):1-29.

[10]Wu X L,Yin Z Y.Global weak solutions for the Novikov equation[J].Journal of Physics A:Mathematical and Theoretical,2011,44(5):1-17.

Peakons and periodic cusp wave solutions of a combination equation

Yang Haixia1,2

(1.Department of Mathematics,Northwest University,Xi′an 710127,China; 2.Center for Nonlinear Studies,Northwest University,Xi′an 710069,China)

In order to study the single-soliton solutions and periodic peakons of a combination equation.By the application of the property of Green′s function,as well as seeking a PDE weak solution approach.The singlesoliton solutions and periodic peakons of the combination equation are obtained.The single-soliton solutions and periodic peakons of the combination equation are constructed,which generalizes the results of previous studies.

Camassa-Holm equation,modified Camassa-Holm equation,Novikov equation, peakons,period peakons

O175.29

A

1008-5513(2013)03-0306-12

10.3969/j.issn.1008-5513.2013.03.013

2013-04-03.

楊海霞(1988-),碩士生,研究方向:非線性偏微分方程

2010 MSC:35J15