一個與吸附劑濃度有關的Langmuir等溫式
趙凌曦 宋淑娥 杜 娜 侯萬國,3,*
(1山東大學環(huán)境研究院,濟南250100;2山東大學膠體與界面化學教育部重點實驗室,濟南250100; 3青島科技大學化學與分子工程學院,生態(tài)化工國家重點實驗室培育基地,山東青島266042)
1 Introduction
During studying the adsorption isotherm at solid-liquid interfaces,an anomalous phenomenon of“sorbent concentration effect”1or“solid effect”2,3(Cs-effect),namely,adsorption isotherm declines as sorbent concentration increases,has been observed since the 1980s.That is to say,the“adsorption equilibrium constant”measured experimentally(or simulated with the classical Langmuir isotherm)for a given system varied with the sorbent(solid)concentration(Cs)utilized in the experimental systems.However,the adsorption equilibrium constant(or equilibrium partition coefficient)for a given adsorption system under constant temperature,pressure,and medium composition(e.g.,pH,ionic strength)should be thermodynamically independent of both sorbate and sorbent concentrations.4
In fact,there has been controversy about the reasons for the Cs-effect over the last thirty years.Some researchers5-8attributed the Cs-effect to a variety of experimental artifacts,while other researchers1,4,9-17believed that the Cs-effect is a constancy phenomenon with thermodynamic principles although many artifacts may cause a pseudo Cs-effect.Just as what McKinley and Jenne16claimed,it seems unlikely that experimental artifacts could explain widespread agreement of a Cs-effect for so diverse adsorption systems and so many investigators because the Cs-effect was observed with many different sorbents including soil,sediment,and clay and with various types of sorbates including inorganic and organic substances.Thus,it can be concluded that the Cs-effect is an experimental fact indeed,not an artifact.There should be a universal reason that causes the Cs-effect although it is still not clear now.
In order to explain the reasons for the Cs-effect or to describe the Cs-effect,many models have been proposed,such as the solute complexation model,1the particle interaction model,9the metastable-equilibrium adsorption(MEA)theory,4the flocculation model,11the power function(Freundlich-like)model,12and the four-component adsorption(FCA)model.13In our previous paper,18a new model,surface component activity(SCA) model,was proposed also.The SCA model suggests that surface component(adsorption site)activity coefficient is not equal to unity while it should be a function of Csbecause of the existence of adsorbent particle-particle interactions,and a semiempirical Cs-dependent function of partition coefficient was derived.It was found that the Cs-dependent function of partition coefficient can describe the Cs-dependence of partition coefficient for both organic compounds and heavy metals.18
The present study attempts to extend the SCA model to describe the Cs-effect phenomena of adsorption isotherms.Thus, a Cs-dependent Langmuir isotherm equation was derived based on the SCA model,and the adsorption tests of Pb(II)and Cu(II)on kaolinite as a function of kaolinite concentration were conducted.As was expected,the Cs-effect was observed in the tests.Then,the applicability of the Cs-dependent Langmuir equation,Langmuir-SCA equation,to describe the Cseffect observed in the adsorption tests was examined.
2 Experimental
2.1 Materials
Kaolinite(chemically pure)was procured from Sinpharm Chemical Reagent Co.,Ltd.,China.The specific surface area and average particle diameter of the kaolinite sample measured by N2adsorption-desorption measurement(Quadrasorb SI-MP system,Quantachrome Instruments,USA)and Zetasizer3000 particle size distribution instrument(Malvern Instruments Ltd., Malvern,UK)are 11.2 m2·g-1and 735 nm,respectively.The other chemicals used in this work were of analytical grade.Ultra pure water was used in all cases.
2.2 Adsorption experiments
Adsorption isotherms of Pb(II)and Cu(II)on a kaolinite sample were carried out by batch equilibration technique.19-21Solutions with various concentrations(0-400 mg·L-1)of Pb(II)and Cu(II)were prepared in 0.01 mol·L-1of NaNO3with Pb(NO3)2and Cu(NO3)2·3H2O,and the pH values of the solutions were adjusted to 5.0 with 0.1 mol·L-1HNO3and NaOH solutions.Known masses of kaolinite samples were mixed with Pb(II)and Cu(II)solutions of various initial concentrations in polyethylene centrifugal tubes.The centrifugal tubes were put into a thermostatic water bath shaker at(25.0± 0.2)°C for 24 h.Then the suspensions were centrifuged at a speed of 4000 r·min-1for 5 min.The Pb(II)and Cu(II)equilibrium concentrations in the supernatants were determined by TAS-990 flame atomic absorption spectrometry(Beijing Purkinje General Instrument Co.,Ltd.).The equilibrium adsorption amounts were calculated using the following equation:

where C0(mg·L-1)and Ce(mg·L-1)are the initial and the remaining(equilibrium)concentrations respectively,Γe(mg·g-1) is the equilibrium adsorption amount,V(mL)is the volume of the suspension,and m(g)is the mass of the kaolinite sample.
The tests were made in triplicate and the finally values were the average of measurements.The relative error was less than 4.34%.
3 Results and discussion
3.1 Adsorption isotherms of Pb(II)and Cu(II)on kaolinite
Fig.1 shows the adsorption isotherms of Pb(II)and Cu(II)on kaolinite at four kaolinite concentrations(25,50,75,and 100 g·L-1).As can be seen,the adsorption isotherms decline significantly as the sorbent concentrations increase.This phenomenon accords with the law which is described by a Cs-effect.
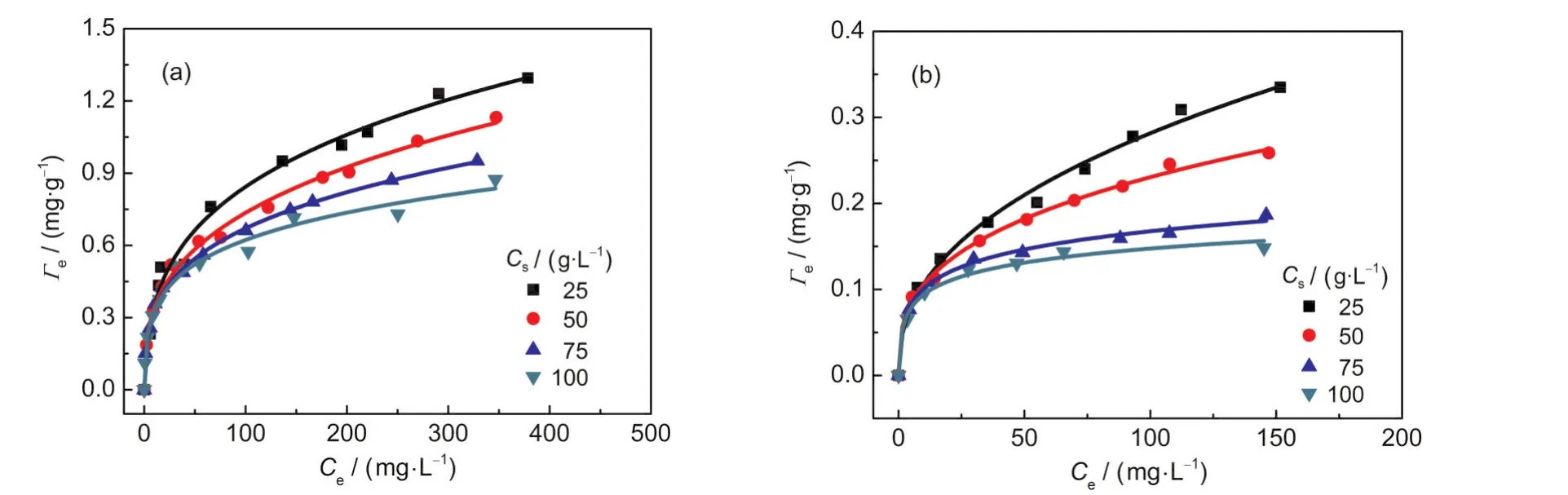
Fig.1 Adsorption isotherms of(a)Pb(II)and(b)Cu(II)on kaolinite at different sorbent concentrations
The classical Langmuir isotherm can be expressed by the following linear form,22,23

where Γmis the maximum sorption amount and KLis Langmuir equilibrium constant.In principle,this equation should be capable of describing the adsorption equilibrium behavior for any given systems,and the two intrinsic parameters,KLand Γm, should be independent of both sorbate and sorbent concentrations.

Fig.2 Linear correlation plots for the classical Langmuir equation(a)Pb-kaolinite system;(b)Cu-kaolinite system
The adsorption data of Pb(II)and Cu(II)on kaolinite(Fig.1) were fitted with the classical Langmuir equation for each kaolinite concentration(Fig.2).It was found that the Langmuir equation can adequately describe the adsorption equilibriums of Pb(II)and Cu(II)on kaolinite for a given Csvalue,and all the correlation coefficients(R2)are greater than 0.95.The fitted Langmuir parameters,Γmand KL,for various Csvalues are presented in Table 1.It can be seen from Table 1 that both Langmuir parameters vary with Csvalue,similar results were reported in the literature.24-26This dependence of the Langmuir parameters on Csviolates the assumptions of the Langmuir theory,showing that the classical Langmuir model cannot describe the Cs-effect.
It should be noted that the basic assumptions of classical Langmuir equation are not easily met under real experimental conditions of metal adsorption using naturally occurring clay minerals.The deviation of a real adsorption system from an ideal one was not accounted in the derivation process of the classical Langmuir equation.This is the reason that classical Langmuir equation cannot describe the Cs-effect observed in batch adsorption tests.
3.2 Surface component activity model
We proposed a surface component activity(SCA)model to describe the Cs-effect of partition coefficient,18now we extendthe SCA model to describe the Cs-effect phenomena of adsorption isotherms.

Table 1 Parameters of the classical Langmuir equation for Pb(II)and Cu(II)adsorption on kaolinite at different sorbent concentrationsa
3.2.1 Theoretical analysis
The SCA model suggests that(1)the surface of sorbent is uniform,that is,all the adsorption sites are equivalent;(2)all adsorption occurs through the same mechanism;(3)at the maximum adsorption,only a monolayer is formed;(4)the molecular sizes of solute and solvent are similar;(5)surface component(adsorption site or adsorbed solute)activity coefficient is not equal to unity because of the deviation of a real adsorption system from an ideal one.
The adsorption process of a solute A in a solvent(H2O)onto a solid surface can be schematically represented as,4

where Site-H2O stands for the solvated site,A for the solute in solution,Site-A for the adsorbed A,and H2O for the solvent in solution.Based on the thermodynamic equilibrium principle,a SCAisotherm equation can be derived as following,18

where Keqis the thermodynamic equilibrium constant for the adsorption process,andare the surface activity coefficients of solvated adsorption sites and adsorbed solutes,respectively,andis the characteristic saturation adsorption capacity for a given system,corresponding to saturated monolayer adsorption of total actual adsorption sites.Bothand Keqare the intrinsic parameters for a given system.They are independent of both sorbate and sorbent concentrations.

or in a linear form,

If the Cs-dependent Langmuir equation is applicable for a given system,the plot of(Cef/Γe)vs Cewill give a line,and theand Keqvalues can be obtained from the slope and intercept of the linear plot.
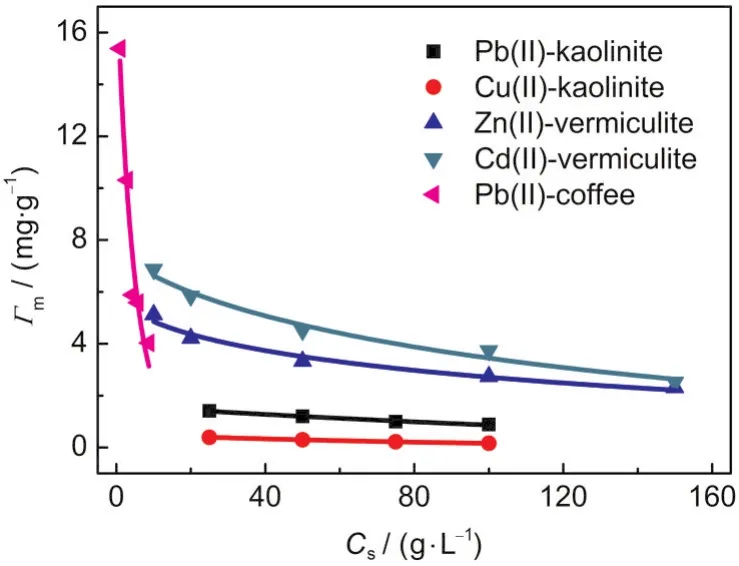
Fig.3 Relationships between Γmand Csin five adsorption systems


where γ and α are empirical constants.Then,we have

or in a linear form,

It is worth to note that the MEAtheory developed by Pan and Liss4provided a reason for the Cs-effect.It suggests that,in reality,the experimentally measured“equilibrium”state of a solid-liquid adsorption system is generally a metastable-equilibrium state.The changes in Cscan affect the metastable-equilibrium adsorption state,in turn,can fundamentally affect the adsorption isotherm.A metastable-equilibrium coefficient Kme(0<Kme≤1)was induced to measure the deviation of a metastable-equilibrium state from the ideal thermodynamic equilibrium state,and a Langmuir-like MEAisotherm was derived.The coefficient Kmewas suggested as a power function of Cs.4In fact, there is a same function form between the Langmuir-SCAequation(based on assuming=1)and Langmuir-type MEA equation,except that the different Cs-dependent function forms were chosen for the correction parameters,and Kme.However,the SCAmodelgivesexplanationfor theCs-effectphenomenon.
3.2.2 Examination of the Cs-dependent Langmuir equation
In order to examine the applicability of the Cs-dependent Langmuir equation to describe the Cs-effect phenomena,the adsorption data,reported in literature,13,15of Zn(II)and Cd(II)on vermiculite13and Pb(II)on coffee15(see Tables S1-S3 in Sup-porting Information)were chosen besides those of Pb(II)and Cu(II)on kaolinite.For the adsorption systems of Cd(II)-vermiculite,Zn(II)-vermiculite,and Pb(II)-coffee reported in literature,13,15each adsorption isotherm at a given Csvalue could be adequately described with classical Langmuir equation.The Langmuir parameters(Γmand KL)simulated from the experimental data of these three systems were dependent on Cs(see Tables S1-S3 in Supporting Information).13,15
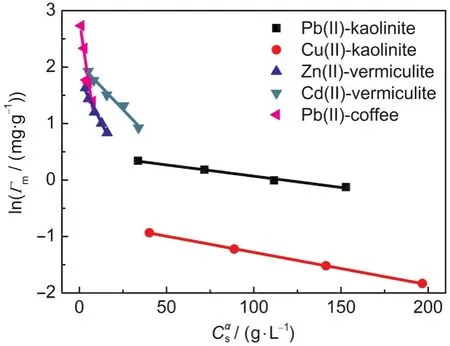
Fig.4 Relationship between lnΓmandCαsin five systems

Table 2 Parameters of the Cs-dependent Langmuir equation for the five adsorption systemsa
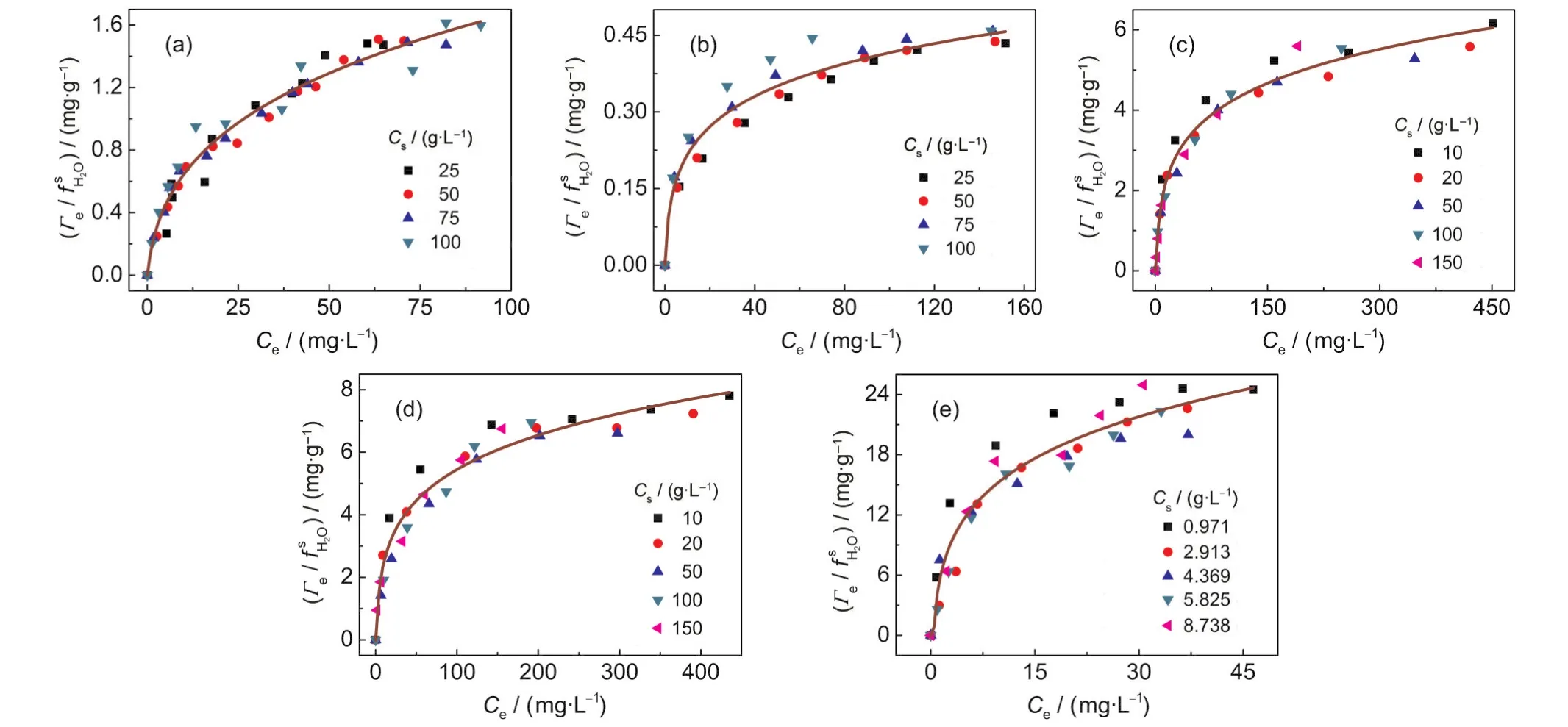
Fig.5 Isotherms of()vs Cefor(a)Pb(II)-kaolinite,(b)Cu(II)-kaolinite,(c)Zn(II)-vermiculite,(d)Cd(II)-vermiculite,and (e)Pb(II)-coffee systems at different sorbent concentrations
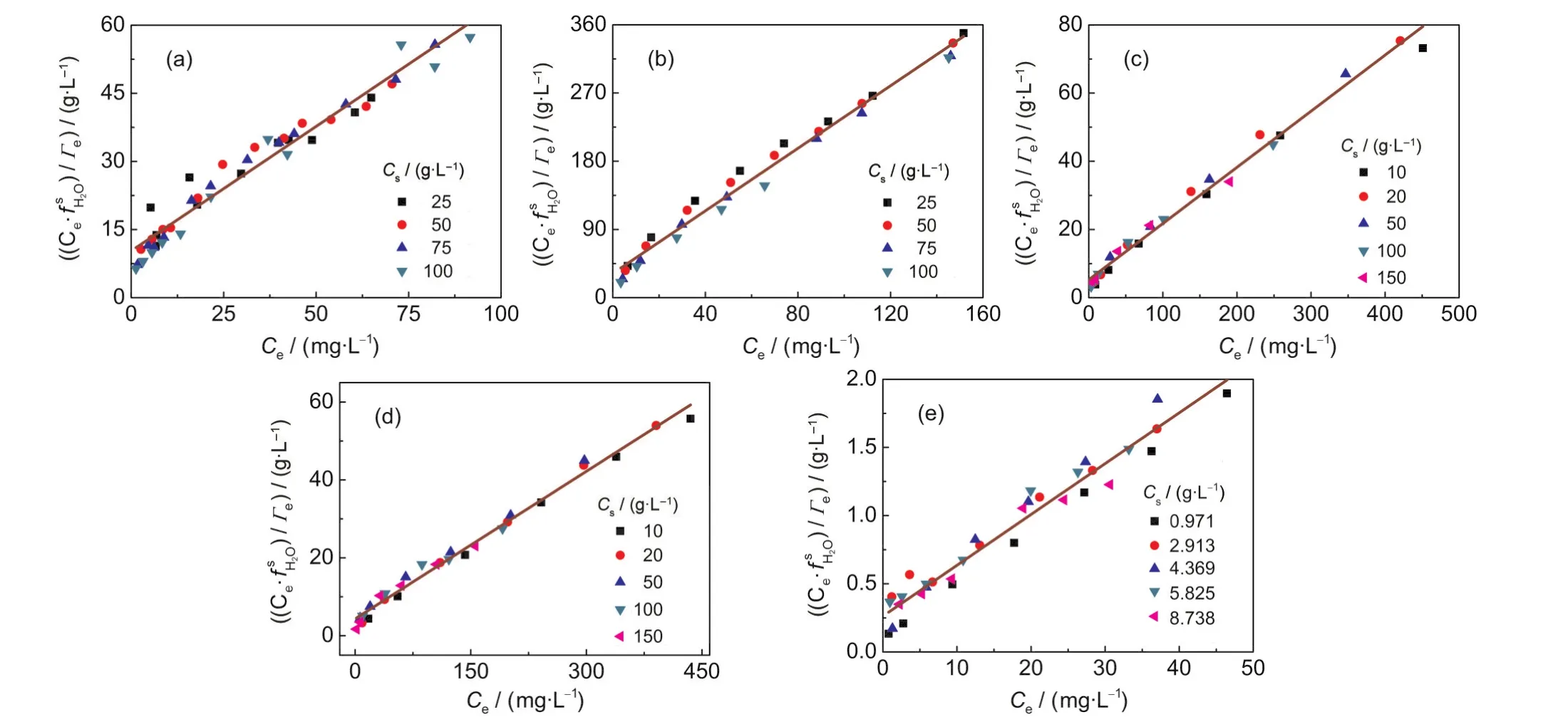
Fig.6 Linear plots of()vs Cefor(a)Pb(II)-kaolinite,(b)Cu(II)-kaolinite,(c)Zn(II)-vermiculite,(d)Cd(II)-vermiculite,and (e)Pb(II)-coffee systems at different sorbent concentrations
The plots of the Γmvs Csfor various adsorption systems are shown in Fig.3.As can be seen,the Γmvalues decrease with increasing Cs,indicating that a pronounced Cs-effect exists in these systems.The changes of the Γmwith Csfor various adsorption systems are fitted to Eq.(9)using a non-linear leastsquares method(Excel Solver).The best-fit values of the empirical constants,α and γ,are listed in Table 2.The plots of lnΓmvsusing the obtained α values in Table 2 are shown in Fig.4,and all the curves are fairly straight lines.
The equation(5)indicates that the isotherm of(Γe/f)plotted against Ceshould be independent of Cs.The non-linear plots of(Γe/f)vs Cefor the various adsorption systems are shown in Fig.5.As expected,all the isotherms of different sorbent concentrations fall onto the same line,that is,a unique curve independent of Csis obtained from experimental data for each given adsorption system.In addition,if the Cs-dependent Langmuir equation is applicable for a given system,the plot of ()vs Ceshould give a line.Fig.6 shows the linear plots of()vs Cefor the various adsorption systems, and all the curves are fairly straight lines.Theand Keqvalues obtained from the slopes and intercepts of the()-Celines are listed in Table 2.Bothand Keqvalues are independent of Csvalue for a given adsorption system,indicating that they are intrinsic parameters.These results indicate that the Csdependent Langmuir equation can describe the Cs-effect observed in the five adsorption systems.Moreover,the assumption of=1 is acceptable.In addition,it is worth to note that for a given sorbent,thevalues in unit of mmol·g-1for different sorbates studied are very close(see Table 2),indicating that theis an intrinsic parameter related to the actual density of adsorption sites of sorbent surface.
4 Conclusions
The Cs-effect phenomena were observed in the adsorptions of Pb(II)and Cu(II)onto kaolinite in the studied conditions.Supposing that the activity coefficient of adsorption sites of sorbent surface is not equal to unity while it should be a function of Cs,a Cs-dependent Langmuir equation was derived based on the SCA model.It was confirmed that the Cs-dependent Langmuir equation can adequately describe the Cs-effect observed in adsorption experiments.At least,it can be considered as a mathematicaltoolfor describingexperimentaldatawithCs-effect.
Supporting Information: available free of charge via the internet at http://www.whxb.pku.edu.cn.
(1) Voice,T.C.;Weber,W.J.Environ.Sci.Technol.1985,19,789. doi:10.1021/es00139a004
(2) O?Connor,D.J.;Connolly,J.P.Water Res.1980,14,1517.doi: 10.1016/0043-1354(80)90018-4
(3) Voice,T.C.;Rice,C.P.;Weber,W.J.Environ.Sci.Technol. 1983,17,513.doi:10.1021/es00115a004
(4) Pan,G.;Liss,P.S.J.Colloid Interface Sci.1998,201,71.doi: 10.1006/jcis.1998.5396
(5) Gschwend,P.M.;Wu,S.C.Environ.Sci.Technol.1985,19,90. doi:10.1021/es00131a011
(6) Cohen-Stuart,M.A.;Scheutjens,J.M.;Fleer,G.J.J.Polymer Sci.:Polymer Physics Ed.1980,18,559.doi:10.1002/pol.1980. 180180315
(7) Nyffeler,U.P.;Li,Y.H.;Santschi,P.H.Geochim.Cosmochim. Acta 1984,48,1513.doi:10.1016/0016-7037(84)90407-1
(8) Grolimund,D.;Borkovec,M.;Federer,P.;Sticher,H.Environ. Sci.Technol.1995,29,2317.doi:10.1021/es00009a025
(9) DiToro,D.M.;Mahony,J.D.;Kirchgraber,P.R.;O?Byrne,A. L.;Pasquale,L.R.;Piccirilll,D.C.Environ.Sci.Technol.1986, 20,55.doi:10.1021/es00143a006
(10) Pan,G.;Liss,P.S.;Krom,M.D.Colloids Surf.A 1999,151, 127.doi:10.1016/S0927-7757(98)00636-0
(11) Helmy,A.K.;Ferreiro,E.A.;Bussetti,S.G.J.Colloid Interface Sci.2000,225,398.doi:10.1006/jcis.2000.6758
(12)Chang,T.W.;Wang,M.K.Chemosphere 2002,48,419.doi: 10.1016/S0045-6535(02)00053-X
(13) Wu,X.F.;Hu,Y.L.;Zhao,F.;Huang,Z.Z.;Lei,D.J.Environ. Sci.2006,18,1167.doi:10.1016/S1001-0742(06)60057-0
(14) Lu,H.J.;Luan,M.T.;Zhang,J.L.;Yu,Y.X.J.China Univ. Mining Technol.2008,18,125.doi:10.1016/S1006-1266(08) 60027-9
(15) Utomo,H.D.;Hunter,K.A.Bioresour.Technol.2010,101, 1482.doi:10.1016/j.biortech.2009.06.094
(16) McKinley,J.P.;Jenne,E.A.Environ.Sci.Technol.1991,25, 2082.doi:10.1021/es00024a015
(17) Fehse,K.U.;Borg,H.;Sokau,E.;Pilchowski,K.;Luckner,L. Water Air Soil Pollut.2010,210,211.doi:10.1007/s11270-009-0243-1
(18) Zhao,L.X.;Hou,W.G.Colloids Surf.A 2012,396,29.doi: 10.1016/j.colsurfa.2011.12.026
(19) Hermosin,M.C.;Pavlovic,L.;Ulibarri,M.A.;Cornejo,J. Water Res.1996,30,171.doi:10.1016/0043-1354(95)00088-3
(20) Ma,L.;Xu,R.K.;Jiang,J.J.Environ.Sci.2010,22,689.doi: 10.1016/S1001-0742(09)60164-9
(21) Ding,P.;Huang,K.L.;Yang,H.;Li,G.Y.;Liu,Y.F.J.Cent. South Univ.Technol.2010,17,277.doi:10.1007/s11771-010-0042-2
(22) Langmuir,I.Am.Chem.Soc.1918,40,1361.doi:10.1021/ ja02242a004
(23) Iraolagoitia,X.L.;Martini,M.F.Colloids Surf.B 2010,76, 215.doi:10.1016/j.colsurfb.2009.10.037
(24)Kim,J.Y.;Shin,M.C.;Park,J.R.;Nam,K.J.Mater.Cycles Waste Manage.2003,5,55.doi:10.1007/s101630300009
(25)Hameed,B.H.;El-Khaiary,M.I.J.Hazard.Mater.2008,154, 639.doi:10.1016/j.jhazmat.2007.10.081
(26) Xu,C.;Li,W.;Pan,G.Acta Phys.-Chim.Sin.2009,25,1737. [徐 從,李 薇,潘 綱.物理化學學報,2009,25,1737.] doi:10.3866/PKU.WHXB20090815

